Количество информации. Лекция 02

1. Информатика

Лекция 2
Количество информации

2. Принципы измерения информации

Количество информации должно обладать
свойствами меры (положительность,
монотонность, аддитивность)
Количество информации зависит от
вероятности наступления события (если
событие наступает с вероятностью 1, то
информация о нем нулевая; чем меньше
вероятность наступления события, тем больше
количество информации о его наступлении)
Получение информации уменьшает
неопределенность при принятии решений

3. Аксиомы количества информации

Пусть событие xi может наступить с вероятностью pi P( xi ) .
Тогда количество информации о наступлении xi есть непрерывная
функция I ( pi ) со свойствами:
1. I ( pi ) 0 ; I (1) 0 .
2. p1 p 2 I ( p1 ) I ( p2 ) .
3. Для независимых событий (т.е. pij P( xi x j ) pi p j )
выполнено I ( pij ) I ( pi ) I ( p j )
Этим аксиомам удовлетворяет функция I ( pi ) log pi .
Основание логарифма определяет только единицу измерения, так
как log a ( p ) log a (b ) log b ( p ) . Если основание логарифма равно 2,
то количество информации измеряется в битах, если e , то в натах,
если 10, то в дитах.

4. Энтропия как мера неопределенности

Пусть источник информации (сообщений) X может находиться в
одном из состояний (посылать одно из сообщений) x1 , x2 , x N с
N
x1 x2 x N
. При этом pi 1 .
вероятностями p1 , p2 , p N . X
i 1
p1 p2 p N
Энтропия этого источника равна
N
H ( X ) pi log pi
i 1
(средневзвешенное количество информации от всех возможных
состояний)
Чем больше число вариантов N , тем больше неопределенность.

5. Свойства энтропии

1. H ( X ) 0
2. Если одно из pi 1, а остальные равны 0, то из log1 0 и
lim ( p log p ) 0 следует H ( X ) 0 , т.е. неопределенность
p 0
отсутствует.
1
3. При заданном N наибольшая энтропия будет, когда все pi .
N
N 1
1
1
1
1
H max log N log log log N
N
N
N
N
i 1 N

6.

x1 x2 x N
и
4. Если даны два независимых источника X
p1 p2 p N
y1 y2 yM
, то их совместное объединение
Y
q1 q2 qM
x1 y1 x1 y2 x1 y M x2 y1 x2 y2 x2 y M x N yM
XY
p1q1 p1q2 p1qM p2 q1 p2 q2 p2 qM p N qM
N M
имеет энтропию H ( XY ) pi q j log( pi q j ) ,
i 1 j 1
которая равна сумме H ( X ) H (Y ) .
Итак, H ( XY ) H ( X ) H (Y ) .

7. Количество информации как мера снятой неопределенности

Пример. Пусть искомый объект находится в одном из четырех
квадратов. Причем все варианты равновозможны.
1
2
3
4
Не зная заранее, где он находится H 0 log 2 4 2 бит. Зададим
вопрос: объект находится в верхней строке? Ответ «да» оставляет
возможными квадраты 1 и 2, ответ «нет» оставляет возможными
квадраты 3 и 4. В обоих случаях остается два варианта и
H 1 log 2 2 1 бит. Количество информации, полученное при
ответе на вопрос, на который можно ответить только «да» или
«нет» равно I1 H 0 H1 2 1 1 бит. Аналогично, ответ на
следующий вопрос: объект находится в левом столбце? также дает
1 бит информации, т.к. H 2 log 2 1 0 и I 2 H1 H 2 1 0 1 .

8. Условная вероятность

Для одновременного наступления двух событий A и B верно
P ( AB ) P ( A) P ( B | A) . Здесь P ( B | A) – вероятность наступления
события B при условии, что A уже произошло. Если A и B
независимы, то P ( B | A) P ( B) и P ( AB ) P ( A) P ( B ) .
Симметрично P ( BA) P( B ) P ( A | B ) , значит
P ( B ) P ( A | B ) P ( A) P ( B | A) .
P ( AB )
Формула условной вероятности P ( A | B )
.
P( B)
P( A | B) P( B )
Формула Байеса P ( B | A)
.
P( A)
Для полной группы событий B1 , B2 , Bn (это значит, они попарно
n
несовместны и P ( Bi ) 1) верна формула полной вероятности
i 1
n
n
i 1
i 1
P ( A) P( ABi ) P( A | Bi ) P ( Bi ) .

9. Условная энтропия

Если два источника сообщений X и Y связаны между собой, то
вероятности появления сообщений y j зависят от сообщений xi .
Энтропия источника Y при условии, что было сообщение xi ,
M
находится по формуле H (Y | xi ) P ( y j | xi ) log P( y j | xi ) .
j 1
Средневзвешенное по всем xi дает полную условную энтропию Y
по отношению к X :
N
M
H (Y | X ) P ( xi ) P( y j | xi ) log P( y j | xi )
i 1
j 1
N M
P ( xi y j ) log P ( y j | xi ) .
i 1 j 1
Совместная энтропия двух источников равна
N M
H ( XY ) P( xi y j ) log P( xi y j ) .
i 1 j 1

10.

Совместная и условная энтропия связаны равенством
H ( XY ) H ( X ) H (Y | X )
N M
Симметрично определяется H ( X | Y ) P( xi y j ) log P( xi | y j ) и
i 1 j 1
доказывается H ( XY ) H (Y ) H ( X | Y ) .
Условная энтропия не больше безусловной
H (Y | X ) H (Y ) ,
потому что добавление ограничений уменьшает неопределенность.
Симметрично доказывается H ( X | Y ) H ( X ) .
Следствие: H ( XY ) H ( X ) H (Y ) .

11. Взаимная информация

N M
Величина I ( X , Y ) P ( xi y j ) log
P ( xi y j )
называется
P ( xi ) P( y j )
взаимной информацией и характеризует количество информации
о сообщениях X , содержащееся в сообщениях Y .
Рассмотрим разность
i 1 j 1
N M
M
H (Y | X ) H (Y ) P ( xi y j ) log P ( y j | xi ) P ( y j ) log P( y j )
i 1 j 1
N
(используем равенство
j 1
P( xi y j ) P( y j ) )
i 1
N M
P( y j | xi )
i 1 j 1
P( y j )
P ( xi y j ) log
N M
P ( xi y j )
i 1 j 1
P ( xi ) P( y j )
P( xi y j ) log
I ( X ,Y )
значит I ( X , Y ) H (Y ) H (Y | X ) 0 .
Симметрично I ( X , Y ) H ( X ) H ( X | Y ) . Взаимная информация –
мера снятой неопределенности при получении сообщений Y .

12.

Таким образом, имеет место полная симметрия между X и Y .
H ( XY ) H ( X ) H (Y | X ) H (Y ) H ( X | Y )
I ( X , Y ) H ( X ) H ( X | Y ) H (Y ) H (Y | X )
H ( XY ) H ( X ) H (Y ) I ( X , Y )
Если X и Y независимы, то H (Y | X ) H (Y ) и H ( X | Y ) H ( X ) ,
значит, I ( X , Y ) 0 и H ( XY ) H ( X ) H (Y ) .
1, при i j
Если X и Y полностью зависимы, то есть P ( y j | xi )
,
0, при i j
тогда H (Y | X ) H ( X | Y ) 0 и I ( X , Y ) H ( X ) H (Y ) H ( XY ) .

13. Два важных случая

Случай 1. Источник с памятью.
Пусть распределение вероятностей появления одного из очередных
сообщений зависит от предыдущих r сообщений, в этом случае
говорят об источнике с памятью размера r .
Предполагается стационарность, т.е. независимость от начала
отсчета времени. Тогда достаточно задать все совместные
вероятности P( xi1 , xi2 , xi M ) , где M .
Такой источник описывается последовательностью условных
энтропий H ( X L | X 1 X 2 X L 1 ) при L .
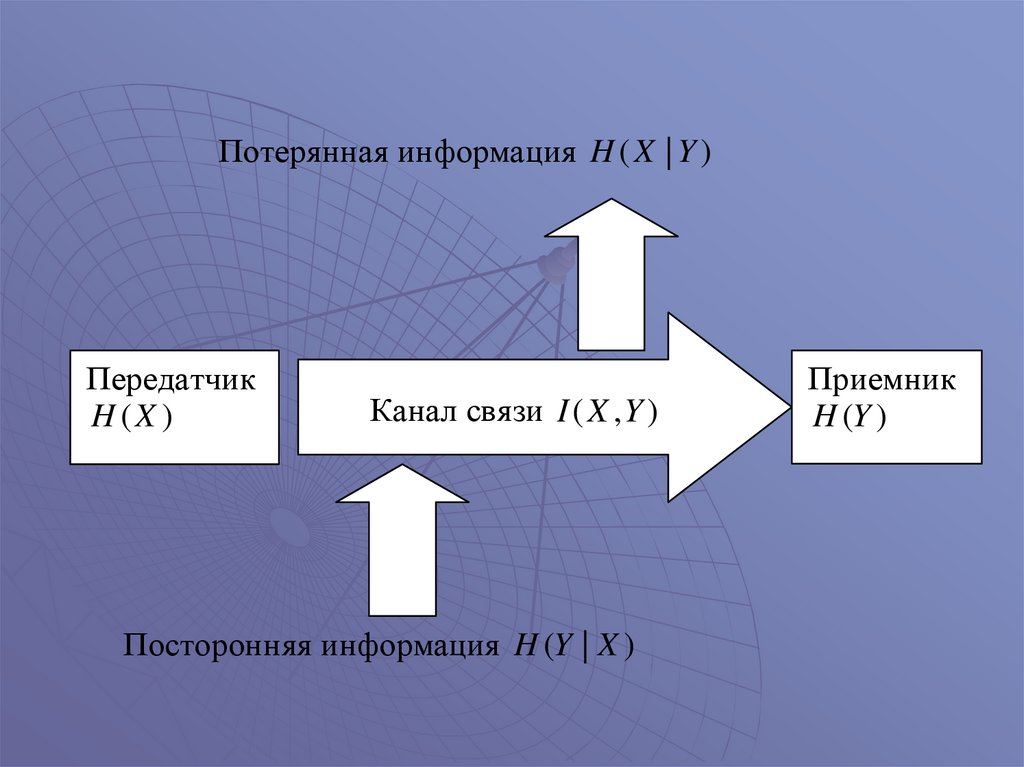
Случай 2. Канал связи с помехами.
X – передаваемые сообщения, Y – принимаемые сообщения.
Из-за помех принимаемые сообщения не всегда совпадают с
передаваемыми. В этом случае рассматриваемые величины
интерпретируются следующим образом:

14.

Потерянная информация H ( X | Y )
Передатчик
H (X )
Канал связи I ( X , Y )
Посторонняя информация H (Y | X )
Приемник
H (Y )

15. Избыточность

В теории информации избыточность означает,
что количество информации в сообщении
меньше чем объем используемого алфавита
От избыточности можно избавиться, применяя
эффективное кодирование, объем сообщения
при этом уменьшается
При передаче по каналу связи с помехами,
наоборот, добавляют проверочные символы
для обнаружения ошибок, увеличивая
избыточность

16.

Пример. Пусть источник задан таблицей
Xi
Pi
a
0,5
b
0,25
c
0,125
d
0,125
Его энтропия H ( X ) 0,5 log 2 0,5 0,25 log 2 0,25 2 0,125 log 2 0,125
0,5 2 0,25 3 0,25 1,75 бит
При обычном кодировании для четырех символов требуется
log 2 4 2 бит на символ (00, 01, 10, 11).
Избыточность D H max H ( X ) 2 1,75 0,25 бит на один
символ.
Для сообщения в 1000000 символов это составит 250 Кбит.