Измерение информации. Информационная характеристика источника двоичных сообщений

1. Измерение информации. Информационная характеристика источника двоичных сообщений.

Лекция 2
1

2. Введение

• Измерение – нахождение значения
физической величины опытным путем с
помощью
специальных
технических
средств.
• Мера
–
средство
измерения,
предназначенное для воспроизведения
заданного значения физической величины
(например, гиря).
2

3. Введение

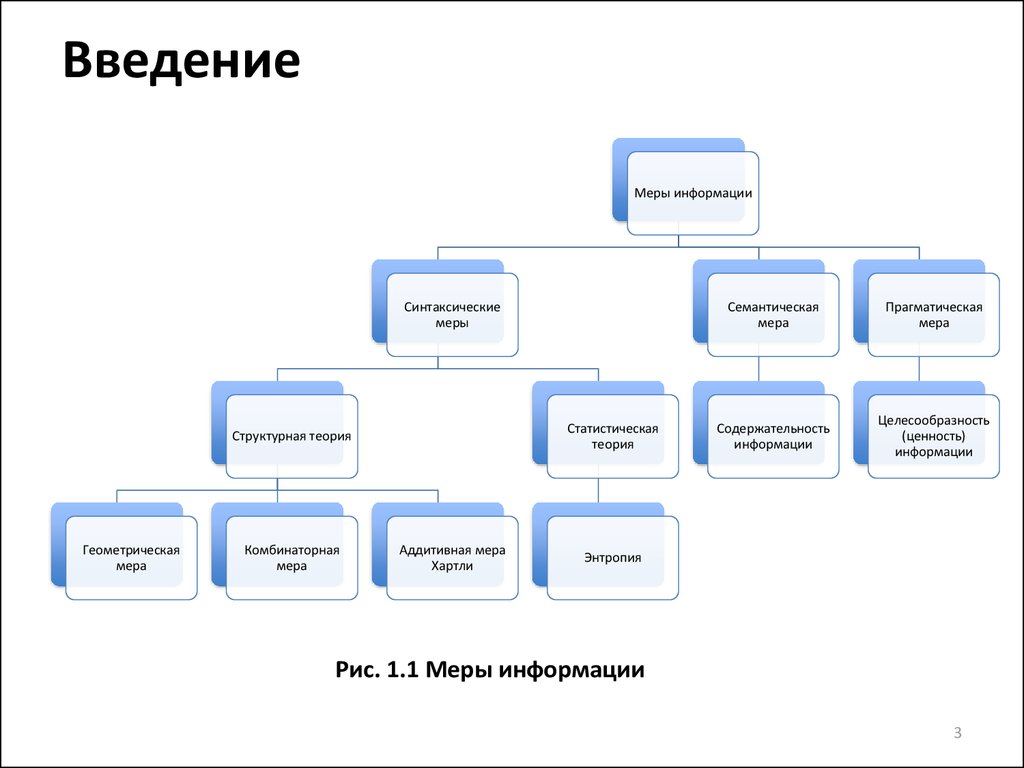
Меры информации
Синтаксические
меры
Статистическая
теория
Структурная теория
Геометрическая
мера
Комбинаторная
мера
Аддитивная мера
Хартли
Семантическая
мера
Прагматическая
мера
Содержательность
информации
Целесообразность
(ценность)
информации
Энтропия
Рис. 1.1 Меры информации
3

4. Введение

В синтаксическом подходе выделяют:
• Структурная
теория
рассматривает
дискретное строение массивов информации и
их
измерение
простым
подсчетом
информационных элементов (квантов).
• Статистическая теория оперирует понятием
энтропии как меры неопределенности,
учитывающей вероятность появления и,
следовательно информативность тех или иных
сообщений.
4

5. 1.1. Синтаксические меры информации. Структурная теория.

1.1.
Синтаксические
Структурная теория.
меры
информации.
При использовании структурной теории
(структурных мер) учитывается только
дискретное
строение
данного
информационного комплекса, в особенности
количество
содержащихся
в
нем
информационных
элементов
(квантов
информации), связей между ними или
комбинацией из них.
5

6. 1.1.1. Геометрическая мера

• Определение
количества
информации
геометрическим
методом
сводится
к
измерению длины лини, площади или объёма
геометрической
модели
данного
информационного комплекса в количестве
дискретных единиц – квантов.
• Геометрическим
методом
определяется
потенциальное (максимально возможное)
количество информации или информационная
ёмкость исследуемого комплекса.
6

7. 1.1.1. Геометрическая мера

• Пусть информация отражается полным комплексом
XTN.
• Если отсчеты по осям X, T, N осуществляются
соответственно через интервалы Δx, Δt, Δn
соответственно, то непрерывные координаты
распадаются на кванты, количество которых
определяется как
mx=X/Δx , mT=T/Δt , mN=N/Δn
• Тогда количество информации в полном комплексе
XTN равно
I=mx mT mN=X T N/(Δx Δt Δn) [ед.]
7

8. 1.1.2. Комбинаторная мера

К этой мере целесообразно прибегать
тогда, когда требуется оценить возможность
передачи
информации
при
помощи
различных комбинаций информационных
элементов.
8

9. 1.1.2. Комбинаторная мера

В комбинаторике рассматривают различные
виды соединения из n элементов по m
элементов, например:
• сочетания Cnm=n!/[m! (n-m)!]
• перестановки Pm=m!
• размещения Anm=n!/(n-m)!=Cnm Pm
9

10. 1.1.2. Комбинаторная мера

• Количество информации в комбинаторной
мере
вычисляется
как
количество
комбинаций информационных элементов.
• Т.е. производится оценка структурного
разнообразия, а не простой подсчет
квантов, как в геометрической мере.
• Количество информации при том же
количестве элементов теперь многократно
увеличивается.
10

11. 1.1.2. Комбинаторная мера

Например, при сочетаниях из n=10 по m=0, 1, 2,
3 …9, 10 элементов имеем
C=10!/0!(10-0)!+10!/1!(10-1)!+…+10!/10!(1010)!=1+10+45+120+210+252+210+120+45+10+1=1024 комбинации
Перестановка тех же элементов дает:
P=10!=3 682 800 комбинаций.
11

12. 1.1.2. Комбинаторная мера

• Не всегда все возможные комбинации
составляют
действительные
степени
свободы данной системы.
• Тогда расчет ведется по реализуемым
комбинациям.
12

13. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• Проводится некий опыт, исход которого
называется событием.
• Например, при бросании монеты имеем 2
состояния: А – появление «орла», В –
появление «решки».
• Разные события обладают разной степенью
возможности, т.о., исход любого опыта –
случайное событие.
13

14. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• Меру
случайности
называют
вероятностью и обозначают P(A).
• Если P(A)=1, то имеем достоверное
событие, если P(A)=0 – невозможное
событие; для всех остальных событий
справедливо 0<P(A)<1.
14

15. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• Событие A называется независимым от
события B, если P(A) не зависит от того,
произошло B или нет.
• В противном случае рассматривают
условную
вероятность
P(A/B)
–
вероятность наступления события A при
условии, что событие B уже произошло.
• Например, вероятность попадания снаряда
в одну и ту же воронку.
15

16. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• События A и B называют несовместными,
если в результате опыта они никогда не
могут появиться одновременно.
• Например, появление «орла» и «решки»
одновременно при бросании монеты.
16

17. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• Суммой событий A и B называется событие,
состоящее в появлении хотя бы одного из
них.
• Произведение событий A и B - событие,
состоящее в появлении обоих.
17

18. 1.1.3. Аддитивная мера Хартли

Из теории вероятностей:
• Совокупность событий составляют полную
группу,
если
в
результате
опыта
непременно должно произойти одно из
них.
• Например, появление любой цифры от 1 до
6 при бросании игральной кости.
• Суммарная вероятность всех входящих в
полную группу событий равна 1.
18

19. 1.1.3. Аддитивная мера Хартли

• Рассмотрим 2 независимых опыта с числом
равновероятных исходов N1 и N2
• Предположим,
что
в
результате
наблюдения за исходами этих опытов
получено количество информации I1=f(N1) и
I2=f(N2)
• Пусть оба опыта проводятся одновременно,
тогда общее число исходов равно N=N1 N2
• При
этом
получаемое
количество
информации I=I1+I2=f(N1 N2)
19

20. 1.1.3. Аддитивная мера Хартли

• Искомая
функция
f(*)
должна
удовлетворять условию: f(N1)+f(N2)=f(N1 N2)
• Единственной функцией удовлетворяющей
этому условию является f(*)=loga(*)
• Формула Р.Хартли (1928 г.) I=logaN
20

21. 1.1.3. Аддитивная мера Хартли

В зависимости от выбора основания
логарифма получаем следующие меры
количества информации:
a=e I=ln N [нит] – натуральные единицы
a=10 I=lg N [дит] – десятичные единицы
a=2 I=ld N [бит] –двоичные единицы
(1 бит информации от английских слов binary
digit)
21

22. 1.1.3. Аддитивная мера Хартли

Иной подход к выводу формулы Хартли:
• Пусть передаваемое сообщение имеет вид числа,
представленного в той или иной системы
счисления.
• Одно и то же количество разрядов в разных
системах счисления может передавать разное число
состояний отображаемого объекта: N=mn ,
где N – число возможных отображаемых состояний;
m – основание системы счисления;
n – число разрядов в сообщении (длина разрядной
сетки).
• Например, при m=100 и n=2 имеем 100 чисел от 00
до 99, а при m=2 и n=2 всего 4 числа: 00, 01, 10 и 11
22

23. 1.1.3. Аддитивная мера Хартли

• В
случае,
когда
все
N
состояний
равновероятны,
получаем
следующую
формулу для оценки количества информации:
I=logaN=n logam
• Если a=m, то I=n, т.е. количество информации
равно объему данных.
• Эту меру можно назвать компьютерной, т.к.
при a=m=2 (двоичная система счисления) и
n=1 (один разряд) имеем единицу измерения
1 бит, от которой производными являются
байт, килобайт, мегабайт и т.д.
23

24. 1.2. Синтаксическая мера. Статистическая теория

• При статистическом (вероятностном)
подходе информация рассматривается как
сообщения о случайных событиях – исходах
некоторого опыта, а количество информации
ставится в зависимость от априорных
вероятностей.
• При бросании кубика: вероятность встретить
один знак (одну из цифр от 1 до 6) в
произвольный момент времени совпадает с
относительной частотой этого знака во всей
последовательно знаков.
24

25. 1.2. Синтаксическая мера. Статистическая теория

• Последовательность знаков с таким
свойством
называется
шенноновским
сообщением.
• Поскольку сами знаки и содержащаяся в
них информация известны заранее,
существенным является сам факт, какой
именно знак выбран.
25

26. 1.2.1. Понятие энтропии

• Упорядоченным называется состояние
системы, осуществляемое относительно
малым числом способов, а беспорядочным
– состояние, реализуемое относительно
большим числом способов.
26

27. 1.2.1. Понятие энтропии

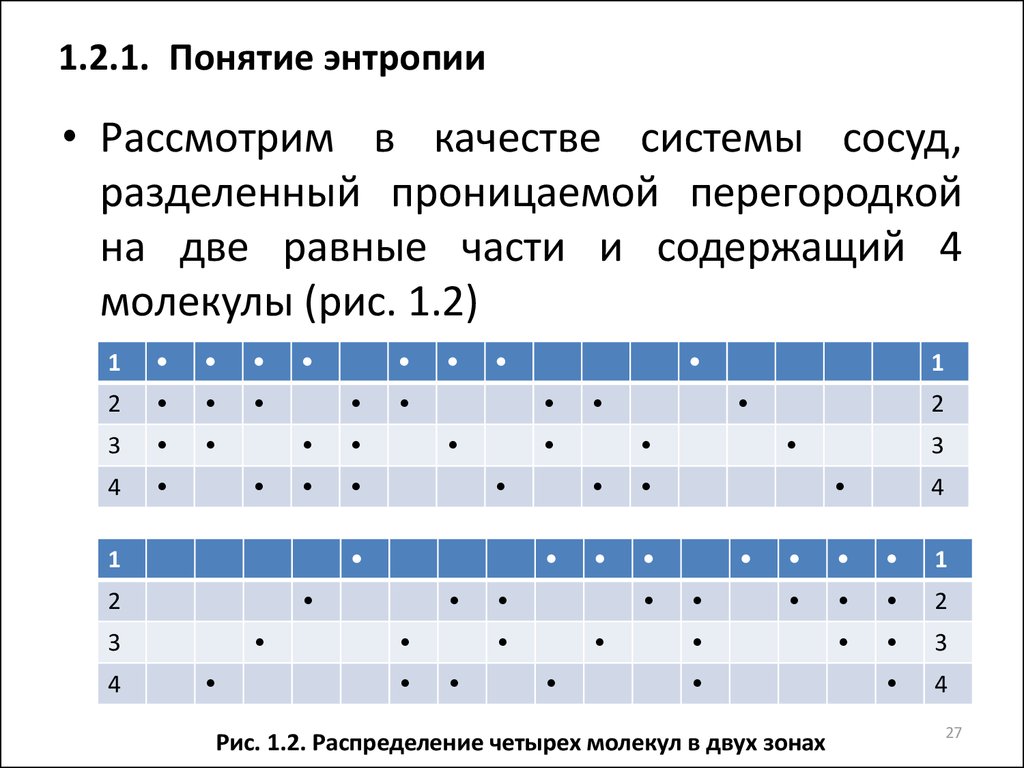
• Рассмотрим в качестве системы сосуд,
разделенный проницаемой перегородкой
на две равные части и содержащий 4
молекулы (рис. 1.2)
1
2
3
4
3
1
2
1
4
2
3
4
1
2
3
4
Рис. 1.2. Распределение четырех молекул в двух зонах
27

28. 1.2.1. Понятие энтропии

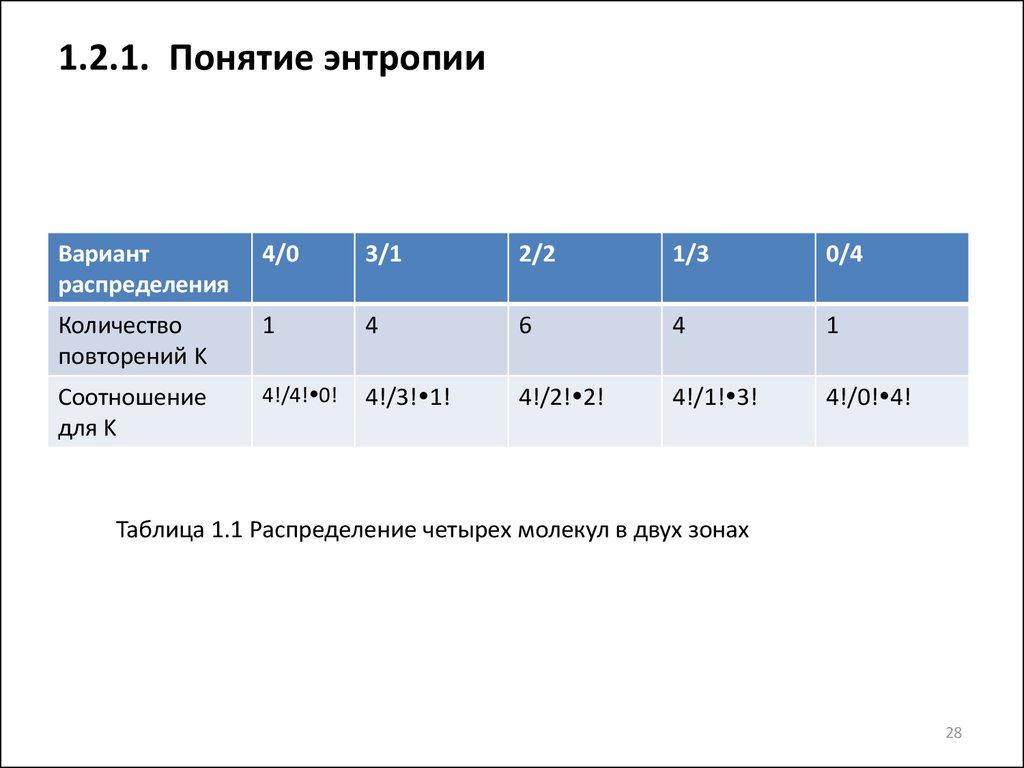
Вариант
распределения
4/0
3/1
2/2
1/3
0/4
Количество
повторений K
1
4
6
4
1
Соотношение
для K
4!/4! 0!
4!/3! 1!
4!/2! 2!
4!/1! 3!
4!/0! 4!
Таблица 1.1 Распределение четырех молекул в двух зонах
28

29. 1.2.1. Понятие энтропии

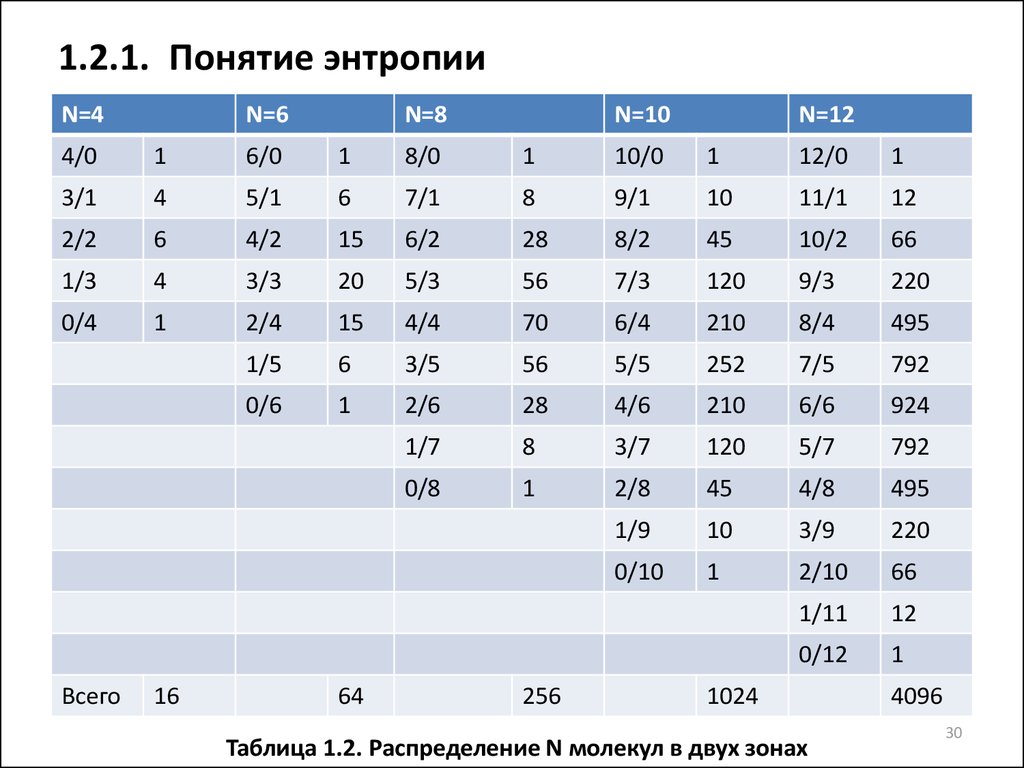
• Формула:
K=N!/(N1! N2!)=N!/[N1! (N-N1)!]
• С увеличением числа молекул различия в
вероятностях будут резко возрастать
(таблица 1.2)
29

30. 1.2.1. Понятие энтропии

N=4
N=6
N=8
N=10
N=12
4/0
1
6/0
1
8/0
1
10/0
1
12/0
1
3/1
4
5/1
6
7/1
8
9/1
10
11/1
12
2/2
6
4/2
15
6/2
28
8/2
45
10/2
66
1/3
4
3/3
20
5/3
56
7/3
120
9/3
220
0/4
1
2/4
15
4/4
70
6/4
210
8/4
495
1/5
6
3/5
56
5/5
252
7/5
792
0/6
1
2/6
28
4/6
210
6/6
924
1/7
8
3/7
120
5/7
792
0/8
1
2/8
45
4/8
495
1/9
10
3/9
220
0/10
1
2/10
66
1/11
12
0/12
1
Всего
16
64
256
1024
Таблица 1.2. Распределение N молекул в двух зонах
4096
30

31. 1.2.1. Понятие энтропии

Вероятность скопления N молекул газа в
одной половине сосуда объемом 1 см3
можно оценить следующим образом:
• для одной молекулы P1=0,5 (да/нет)
• при нормальных условиях в 1 см3
содержится L=2,7 1019 молекул газа (число
Лошмидта)
• Тогда для N молекул имеем PN=P1N=0,51=2-1
31

32. 1.2.1. Понятие энтропии

Второй закон термодинамики:
Природа стремится от состояний менее
вероятных к состояниям более вероятным (Л.
Больцман).
32

33. 1.2.1. Понятие энтропии

Пример:
Если взять 4-разрядные двоичные числа, то в
6 комбинациях из 16 возможных имеем
равное количество 0 и 1 (табл. 1.3)
0 0 0 0
0 1 0 0
1 0 0 0
1 1 0 0
0 0 0 1
0 1 0 1
1 0 0 1
1 1 0 1
0 0 1 0
0 1 1 0
1 0 1 0
1 1 1 0
0 0 1 1
0 1 1 1
1 0 1 1
1 1 1 1
Таблица 1.3. Распределение 0 и 1 в двоичных числах
33

34. 1.2.1. Понятие энтропии

• Энтропия в термодинамике – количественная
мера неупорядоченности, мера вероятности
осуществления
какого-либо
состояния
системы.
• В физику понятие энтропии ввел Рудольф
Клаузиус (19 в.).
• Л. Больцман использовал это понятие для
определения меры необратимого рассеяния
энергии, что позволило строго математически
сформулировать
второй
закон
термодинамики.
34

35. 1.2.1. Понятие энтропии

Статистический смысл второго закона
(начала) термодинамики:
Макроскопическое
состояние
газа
с
некоторыми значениями
параметров
представляет собой смену микроскопических
состояний, которые отличаются одно от
другого нахождением одних и тех же молекул
в
разных
частях
объема
и
перераспределением энергии между этими
молекулами.
35

36. 1.2.1. Понятие энтропии

В соответствии со вторым законом для
замкнутого пространства (изолированной
системы) энтропия равна
S=-1/N Σni ln(ni/N)=-Σpi ln pi
где N-общее число молекул в системе;
pi – вероятность того, что ni молекул имеют
скорости vi+Δvi
36

37. 1.2.1. Понятие энтропии

Иная трактовка
- энтропия как мера
вероятности осуществления какого-либо
состояния системы:
S=-Σpi ln pi =k lnW
где pi – вероятность нахождения молекул в i-й
ячейке фазового пространства; W –
термодинамическая вероятность данного
макроскопического состояния системы или
число соответствующих состояний; k=1,38 1023 Дж/К – постоянная Больцмана.
37

38. 1.2.1. Понятие энтропии

Третий смысл энтропии получается из
понятия упорядоченности: коль скоро
неупорядоченные
состояния
системы
достижимы большим числом способов и
поэтому более вероятны, то энтропия
оказывается и мерой неупорядоченности
системы.
38

39. 1.2.2. Мера Шеннона

• Энтропия в теории информации –
количественная мера неопределенности.
• Трактовку ввел в 1948 г. Клод Шеннон
39

40. 1.2.2. Мера Шеннона

• Главным свойством рассмотренных опытов
является неопределенность, т.к. каждый исход
– случайное событие.
• Важно уметь численно оценить степень
неопределенности, чтобы иметь возможность
объективного сравнения различных опытов.
• Степень неопределенности опыта, имеющего
N исходов, зависит от N: если при N=1 исход
опыта вообще не является случайным, то по
мере возрастания N предсказание того или
иного
исхода
становится
все
более
проблематичным.
40

41. 1.2.2. Мера Шеннона

• Для опыта с N равновероятными исходами
x1, x2,…xN (полная группа случайных
событий) таблица вероятностей имеет вид:
Исходы
x1
x2
xN
Вероятности
1/N
1/N
1/N
41

42. 1.2.2. Мера Шеннона

• Рассматривая количество информации как
меру неопределенности такого опыта в
соответствии с формулой Хартли имеем
I= ld N [бит]
• При этом каждый исход имеет
неопределенность
Ik=(1/N) ld N=-(1/N) ld (1/N) [бит]
42

43. 1.2.2. Мера Шеннона

• В общем случае для опыта
неравновероятными исходами:
Исходы
x1
x2
xN
Вероятности
p1
p2
pN
с
N
• Мера неопределенности:
H(X)=-p1 ld p1-p2ld p2 -…-pN ld pN [бит]
43

44. 1.2.2. Мера Шеннона

• H(X) – энтропия случайного опыта или
просто энтропия.
H(X)=-Σpi ld pi при Σpi=1
• Это
основное
определение
теории
информации Шеннона.
• Количественно выражается как средняя
функция каждого из возможных исходов
опыта.
• Формула Хартли является предельным
случаем формулы Шеннона.
44

45. 1.2.2. Мера Шеннона

• Единице измерения энтропии 1 бит
соответствует опыт, имеющий N=2
равновероятных исходов
H(X)=-1/2 ld ½-1/2 ld ½=1/2+1/2=1 [бит]
45

46. 1.2.2. Мера Шеннона

Сопоставление термодинамической формулы
(Больцмана) и информационной (Хартли и
Шеннона) трактовок понятия энтропии приводит
к фундаментальному соотношению фон
Неймана,
связывающему
энергию
и
информацию:
E0=k T ln2 [Дж/бит]
Где E0 – количество энергии, требуемое для
обработки 1 бита информации при заданном
значении термодинамической температуры, k –
постоянная Больцмана
46

47. 1.2.3. Свойства энтропии

H(X) – величина вещественная и неотрицательная
H(X)min=0 когда pk=1, pi=1
H(X)max=ld N когда pi=1/N
H(X)min<H(X)<H(X)max
H(X)>=H(f(X)) при любой функции f(X)
Для двух независимых опытов X и Y,
осуществляемых одновременно H(X,Y)=H(X)+H(Y)
• Для двух зависимых опытов X и Y,
осуществляемых
одновременно
H(X,Y)=H(X)+HX(Y)=H(Y)+HY(X), где HX(Y) – условная
энтропия Y
47

48. 1.2.3. Свойства энтропии

Рис.1.3 Энтропия опыта с двумя исходами
48

49. 1.2.4. Количество информации

• Условная энтропия HY(X) является мерой
остаточной неопределенности.
Рис.1.4. Упрощенная схема передачи сообщений
49

50. 1.2.4. Количество информации

• Пусть источник сообщений (испытатель), наблюдая за
случайными исходами, генерирует и передает исходное
сообщение X, характеризуемое энтропией H(X).
• После прохождения через канал связи это сообщение
преобразуется в принятое (конечное) сообщение Y,
характеризуемое
энтропией
H(Y),
которое
и
воспринимает получатель.
• Т.к. получатель не имеет прямого доступа к опыту, он
оценивает его исходы только по сообщению Y.
• В результате для получателя неопределенность
ситуации уменьшилась на величину HY(X) – энтропия
сообщения X при условии, что получено сообщение Y.
• Разность
H(X)-HY(X)
называется
неэнтропией
(отрицательная энтропия), т.к. Определяет уменьшение
энтропии за счет передачи сообщения, служит мерой
количества информации при передаче сообщения.
50

51. 1.2.4. Количество информации

• Количество
информации
–
числовая
характеристика сигнала, позволяющая оценить
исходную степень неопределенности, которая
исчезает после выбора (получения) сообщения
в виде данного сигнала.
• Количество информации – мера уменьшения
неопределенности
ситуации
(случайной
величины) X, возникающая вследствие того,
что становятся известными исходы другой
ситуации
(случайной
величины)
Y,
усредненная по исходу X и Y:
I(X,Y)=H(X) –HY(X)
51

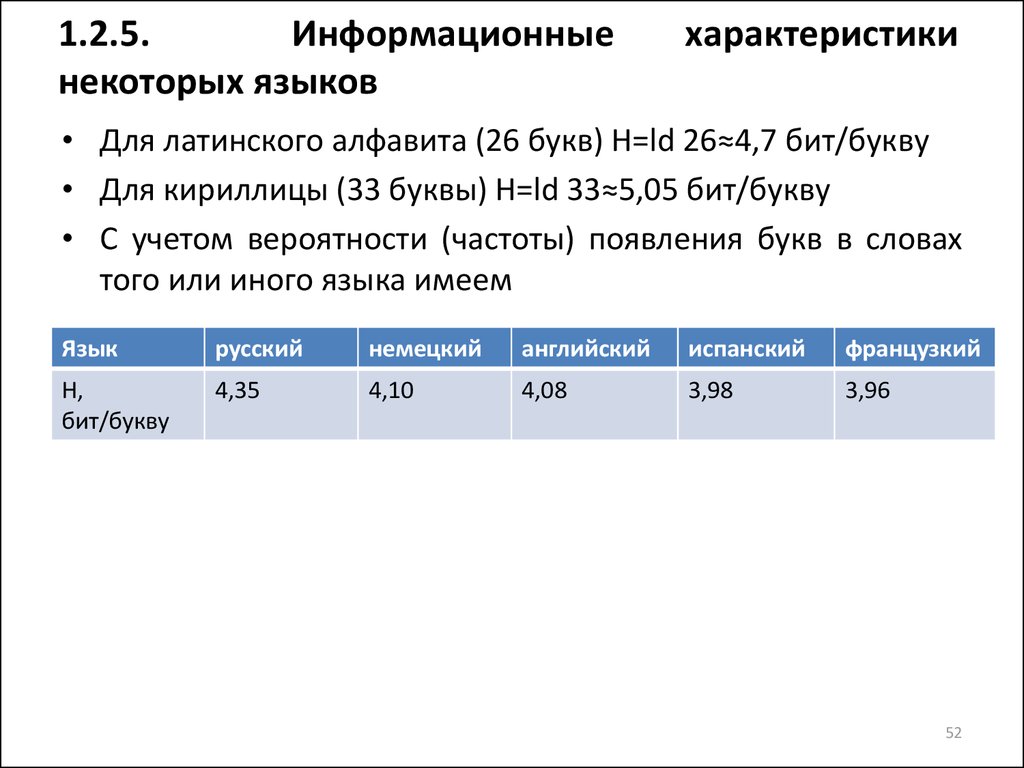
52. 1.2.5. Информационные характеристики некоторых языков

1.2.5.
Информационные
некоторых языков
характеристики
• Для латинского алфавита (26 букв) H=ld 26≈4,7 бит/букву
• Для кириллицы (33 буквы) H=ld 33≈5,05 бит/букву
• С учетом вероятности (частоты) появления букв в словах
того или иного языка имеем
Язык
русский
немецкий
английский
испанский
французкий
H,
бит/букву
4,35
4,10
4,08
3,98
3,96
52

53. 1.3. Семантическая и прагматическая меры информации

• Рассмотрим оценки, отвечающие как
семантическому, так и прагматическому
подходам.
• Это обусловлено тем, что в инженерных
применениях
прагматические
оценки
сливаются с семантическими: не имеющие
смысла
сведения
бесполезны,
а
бесполезные знания бессмысленны.
53

54. 1.3.1 Содержательность информации

• Оценка содержательности основана на
математической
логике,
в
которой
логические функции истинности m(A) и m(ØA)
имеют формальное сходство с функциями
вероятностей наступления события P(A) и
антисобытия P(ØA)
• m(A) + m(ØA) =1
P(A) + P(ØA) =1
• cond-мера содержательности сообщения z
cont(z)
P( = m(
cond(z) = m(Øz) =1- m(z)
54

55. 1.3.1 Содержательность информации

• Логическая оценка информации:
Inf = ld[1/ (1- cont(z)] = ld(1/ m(z)) = -ldm(Øz)
• Отличие
статистической
оценки
от
логической состоит в том, что в первом
случае
учитываются
вероятности
реализации тех или иных событий (исходов
опытов), а во втором – меры истинности,
что приближает к оценке смысла
информации.
55

56. 1.3.2 Целесообразность информации

• А.А.Харткевичем
предложена
мера
целесообразности
информации,
которая
определяется
как
изменение
вероятности
достижения цели при получении дополнительной
информации.
• Полученная информация может не изменять
вероятности достижения цели (ситуация не
изменилась), тогда ее мера равна 0.
• Информация может уменьшать вероятность
достижения цели (дезинформативность, ситуация
ухудшилась), тогда ее мера отрицательна.
• Информация может увеличивать вероятность
достижения
цели
(добротная
информация,
ситуация улучшилась), тогда ее мера положительна.
56

57. 1.3.2 Целесообразность информации

Мера целесообразности в общем виде
может выть выражена соотношением
I=Ld p1-ld p0=ld(p1/p0)
где p0, p1 – начальная (до получения
информации) и конечная (после получения
информации) вероятности достижения цели
57

58. 1.3.2 Целесообразность информации

Рис.1.5. Пути движения к цели
58

59. 1.3.2 Целесообразность информации

• Пусть
имеется
некоторое
исходное
состояние (точка 1), цель (точка 3), и
некоторое
промежуточное
состояние
(точка2).
• Из точки 1 возможны 2 пути: 1-2 и 1-3.
• Если пути к цели априорно неизвестны, то
можно предположить, что вероятности ее
достижения по обоим путям равны, т.е. P(12)=P(1-3)=1/2
59

60. 1.3.2 Целесообразность информации

• Предположим, что достигнута точка 2, и при этом
получена нейтральная информация: с равным
успехом можно двигаться как по пути 2-3, так и по
пути 2-4
• Тогда I=ld[P(2-3)/P(1-2)]=ld(1/2)-ld(1/2)=0
• Предположим, что достигнута точка 2, и при этом
получена ложная информация: пять направлений из
шести ведут по пути 2-4 и только одно – по пути 2-3.
• Тогда I=ld[P(2-3)/P(1-2)]=ld(1/6)-ld(1/2)=-ld 6+ld 2=-1,58
• Предположим, что достигнута точка 2, и при этом
получена благоприятная информация: два направления из
шести ведут по ложному пути 2-4 и четыре направления –
по пути 2-3
• Тогда I=ld[P(2-3)/P(1-2)]=ld(4/6)-ld(1/2)=ld 4- ld 6 +ld 2=0,42
60