Similar presentations:
Теория информации. Лекция №5
1.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
Лекция № 6
Часть 1. Результаты Шеннона и проблемы кодирования
1. Теорема Шеннона для канала без помех
2. Теорема Шеннона для канала с помехами
3. Значение результатов Шеннона для задач передачи, хранения и поиска
информации
4. Современные технические средства передачи информации
Часть 2. Эффективное кодирование
1. Сжатие данных
2. Сжатие на основе статистических свойств данных
2.1. Коды с переменной длиной кодового слова
2.2. Вероятностная модель кодируемых сообщений
2.3. Минимизация средней длины кодового слова
1
2.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Лекция № 5
Часть 1. Условная энтропия и взаимная информация
1.1. Условная энтропия
1.2. Взаимная информация
1.3. Пример с троичным каналом
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи без помех
2.3. Обобщенные характеристики сигналов и каналов
Часть 3. Каналы передачи информации с помехами
3.1. Вероятностные модели каналов передачи информации:
– двоичный канал
– троичный канал
3.2. Характеристики каналов передачи информации с помехами
1
3.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Часть 1. Условная энтропия и взаимная
информация
1. Условная энтропия
2. Взаимная информация
I ( , ) H ( ) H ( ).
3. Пример с троичным каналом
N
M
H (Y / X ) p ( xi y j ) log 2
i 1 j 1
1
p( y j / xi )
.
2
4.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
1. Условная энтропия
Пусть ξ и η – случайные величины с множествами возможных
значений X = {x1,x2,…, xn}, Y = {y1,y2,…, ym}
Количество информации H(ξ) при наблюдении случайной величины
ξ X = {x1,x2,…, xn} с распределением вероятностей P = {p1, p2, …,
pn} задается формулой Шеннона:
n
H ( ) pi log 2l / pi
i l
Количество информации H(η) при наблюдении случайной величины
η Y = {y1,y2,…, ym} с распределением вероятностей Q = {q1, q2, …,
qm} задается формулой Шеннона:
m
H ( ) qi log 2l / qi
i l
3
5.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
3
1. Условная энтропия
Условной энтропией величины η при наблюдении величины ξ называется
N
M
1
H ( ) H ( / ) H (Y / X ) p(xi y j ) log 2
.
p( y j / x i )
i 1 j 1
Справедливы соотношения:
H ( , ) H ( ) H ( ),
N
M
1
H ( , ) p(x i y j ) log 2
.
p( y j x i )
i 1 j 1
6.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Часть 1. Условная энтропия и взаимная
информация
1. Условная энтропия
I
(
,
)
H
(
)
H
(
).
2. Взаимная информация
3. Пример с троичным каналом
N
M
H (Y / X ) p ( xi y j ) log 2
i 1 j 1
1
p( y j / xi )
.
4
7.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
7
2. Взаимная информация
Взаимной информацией величин ξ и η называется I ( , ) H ( ) H ( ).
Справедливы следующие соотношения:
N
M
I ( , ) p (x i y j ) log 2
i 1 j 1
p(x i y j )
p(x i ) p( y j )
,
I ( , ) I ( , ) H ( ) H ( ),
I ( , ) H ( ) H ( ) H ( , ),
Закон аддитивности в общем случае:
H ( , ) H ( ) H ( ) I ( , ),
0 I ( , ) H ( ), 0 I ( , ) H ( ).
Если ξ и η – независимы, то I(ξ, η) = 0.
8.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
8
2. Взаимная информация
При расчетах условной энтропии и взаимной информации удобно пользоваться
следующими соотношениями теории вероятностей:
1) теорема
умножения вероятностей
p(x i y j ) p(x i ) p( y j / x i ) p( y j ) p(x i / y j )
M
2) формула полной вероятности
p(xi ) p(xi , y j );
j 1
3) формула Байеса
p(x i / y j )
p(x i ) p( y j / x i )
p( y j )
p(x i ) p( y j / x i )
N
p(x ) p( y / x )
i
i 1
j
i
.
9.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Часть 1. Условная энтропия и взаимная
информация
1. Условная энтропия
2. Взаимная информация
I ( , ) H ( ) H ( ).
3. Пример с троичным каналом
N
M
H (Y / X ) p ( xi y j ) log 2
i 1 j 1
1
p( y j / xi )
.
7
10.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
3. Пример с троичным каналом (с матрицей)
Пример 1. Дана матрица
1 1 1
8 8 8
1
1
P( X , Y )
0
X , Y
8
8
1 1 1
8 8 8
Определить: H( ), H( ), H ( ), H ( ), H( , ), I ( , ).
Решение. По формуле полной вероятности имеем:
3
P ( x1 ) p ( x1 , y j )
j 1
3
1
, P (x 2 ) ,
8
4
3
3
3
P ( x 3 ) , P ( y1 ) p ( x i , y1 ) , P ( y 2 ) 1 , P ( y 3 ) 3 .
8
8
4
8
i 1
3
3
1
Следовательно, H ( ) p( xi ) log 2
1,57;
p
(
x
)
i 1
i
H ( ) p( yi ) log 2
i 1
1
1,57.
p( y i )
10
11.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 5 курс
Лекция № 5
3. Пример с троичным каналом (с матрицей)
По теореме умножения
1
,
3
p( x1 / y 2 )
1
,
2
p( x2 / y2 ) 0,
p( x 2 / y 3 )
1
,
3
p ( x 1 / y 1 ) p ( x 1 y 1 ) / p ( y1 )
p ( x 2 / y1 )
1
,
3
p ( x 3 / y1 )
1
1
1
, p( x 3 / y 2 ) , p ( x 3 / y 3 ) .
3
2
2
p( x 1 / y 3 )
1
,
3
Следовательно,
3
3
H ( ) p( xi y j ) log 2
I 1 J 1
Аналогично
1
1,43.
p( x i / y j )
H ( ) 1,43; H ( , ) H ( ) H ( ) 3; I ( , ) H ( ) H ( ) 0,14.
11
12.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Лекция № 5
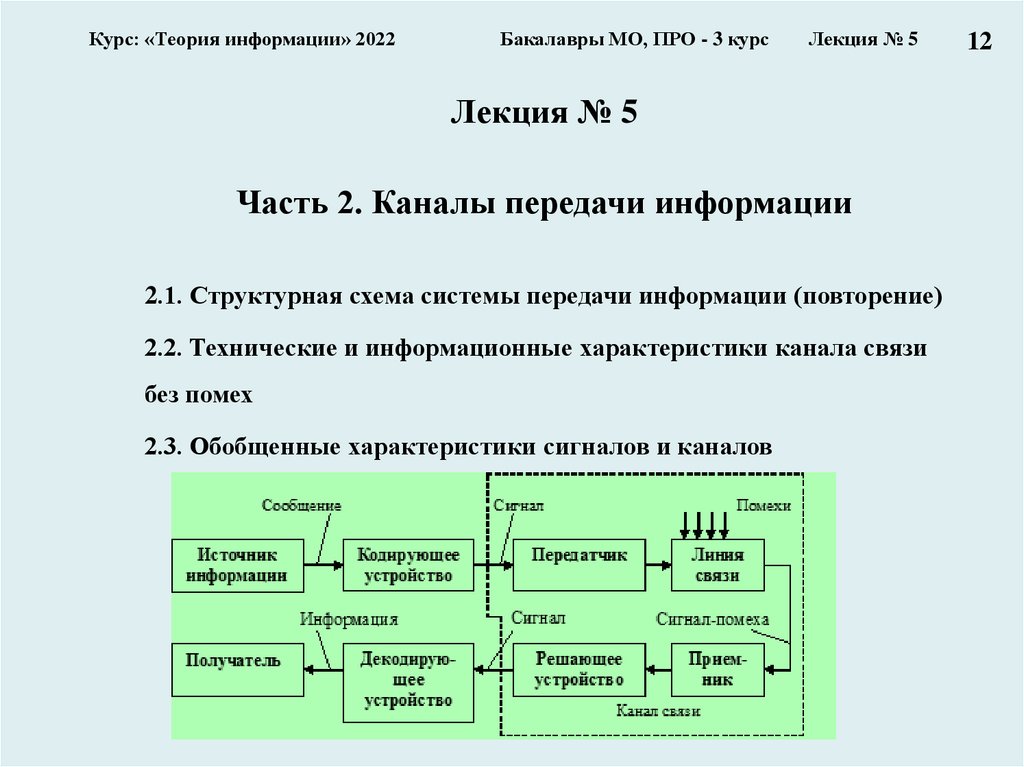
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи
без помех
2.3. Обобщенные характеристики сигналов и каналов
12
13.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
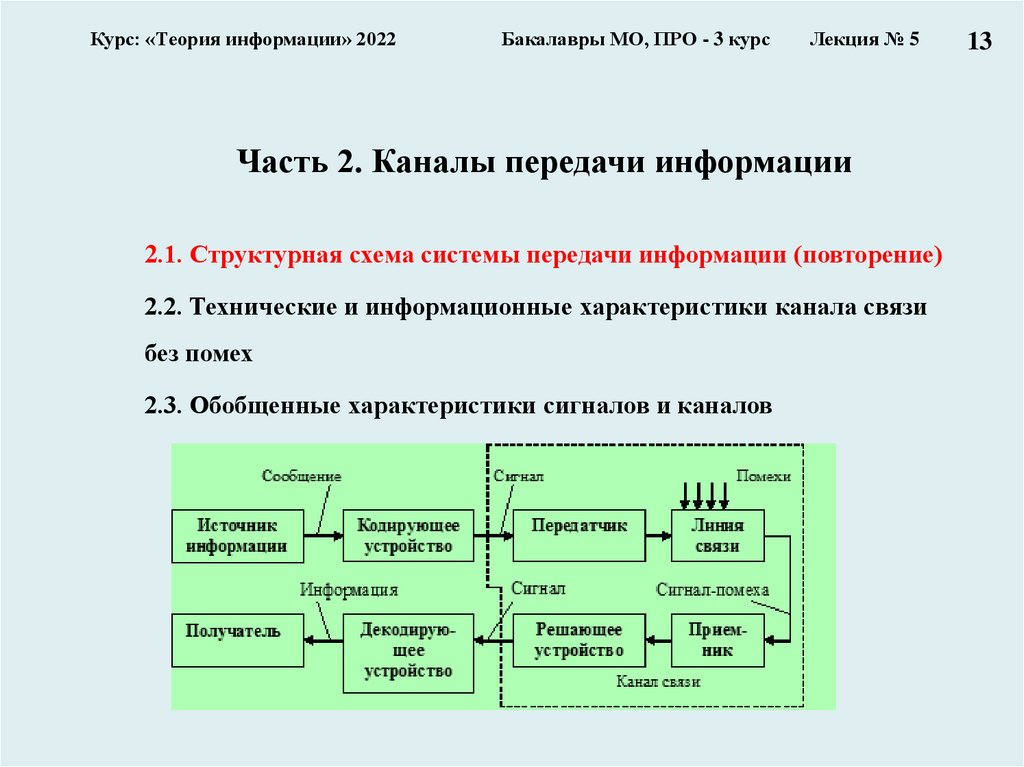
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи
без помех
2.3. Обобщенные характеристики сигналов и каналов
13
14.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
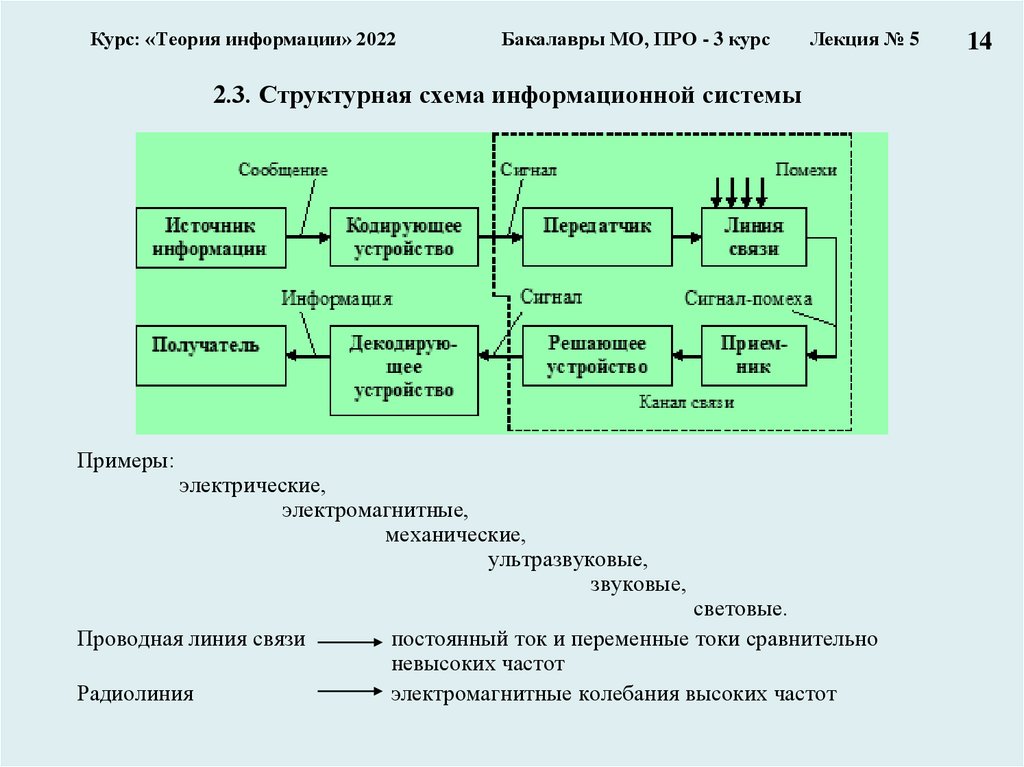
2.3. Структурная схема информационной системы
Примеры:
электрические,
электромагнитные,
механические,
ультразвуковые,
звуковые,
Проводная линия связи
Радиолиния
световые.
постоянный ток и переменные токи сравнительно
невысоких частот
электромагнитные колебания высоких частот
14
15.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
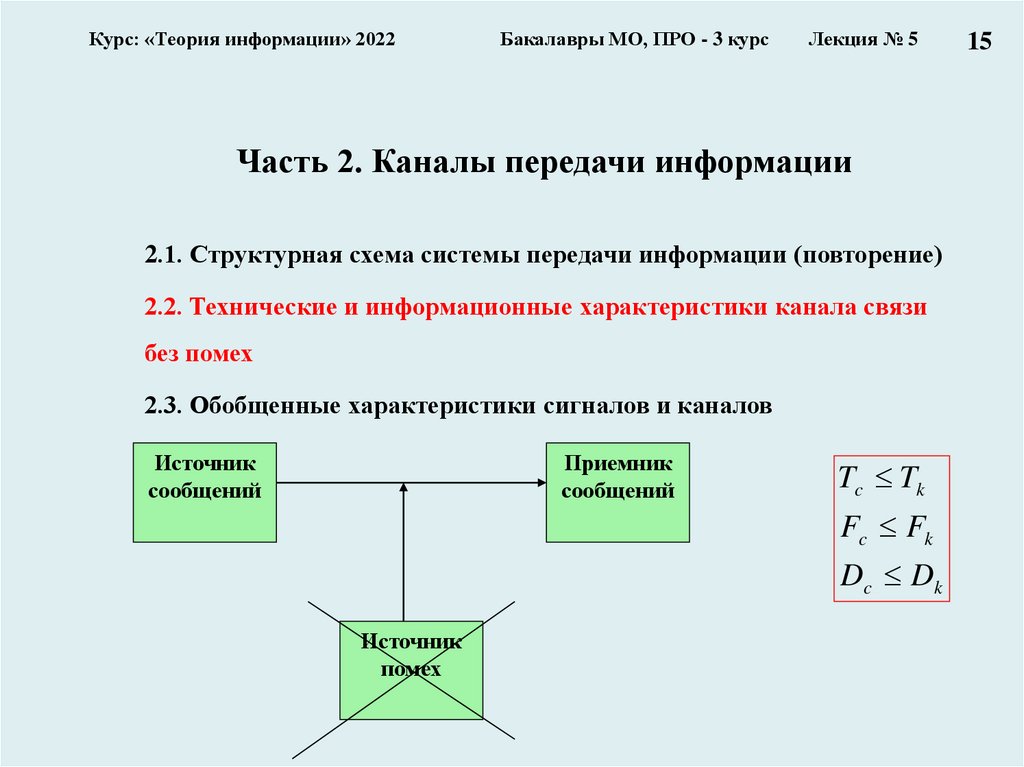
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи
без помех
2.3. Обобщенные характеристики сигналов и каналов
Источник
сообщений
Приемник
сообщений
Tc Tk
Fc Fk
Dc Dk
Источник
помех
15
16.
Курс: «Теория информации» 20222.
Бакалавры МО, ПРО - 3 курс
Лекция № 5
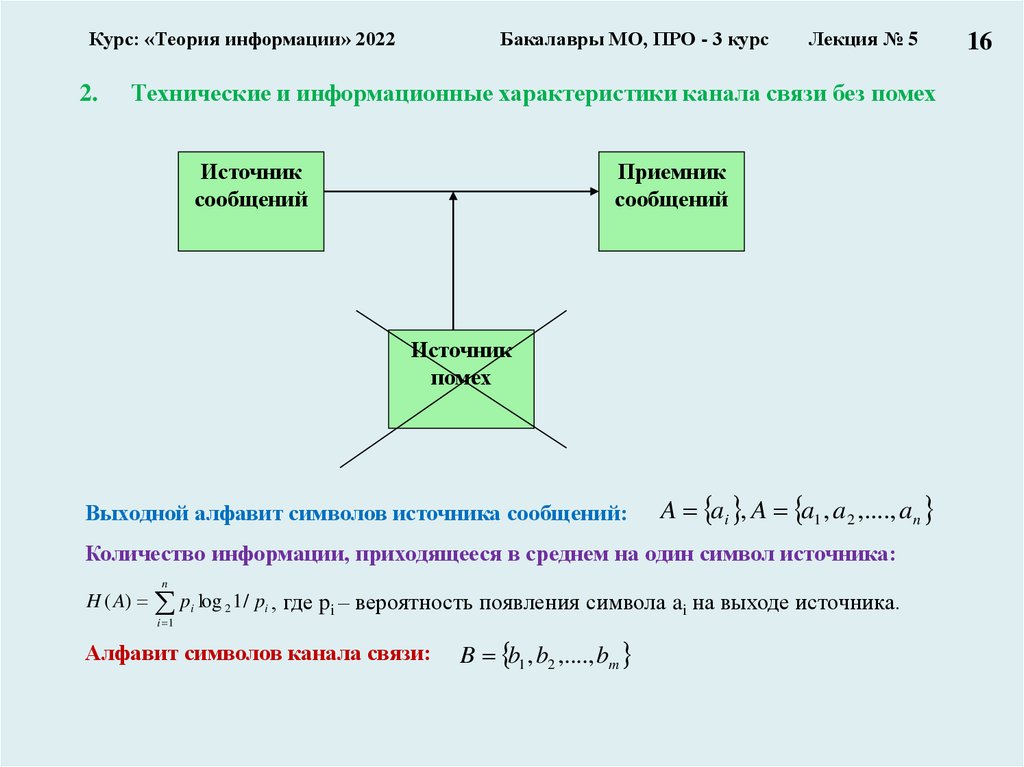
Технические и информационные характеристики канала связи без помех
Источник
сообщений
Приемник
сообщений
Источник
помех
Выходной алфавит символов источника сообщений:
A ai , A a1 , a2 ,...., an
Количество информации, приходящееся в среднем на один символ источника:
n
H ( A) pi log 2 1 / pi , где pi – вероятность появления символа ai на выходе источника.
i 1
Алфавит символов канала связи:
B b1 , b2 ,...., bm
16
17.
Курс: «Теория информации» 20222.
Бакалавры МО, ПРО - 3 курс
Лекция № 5
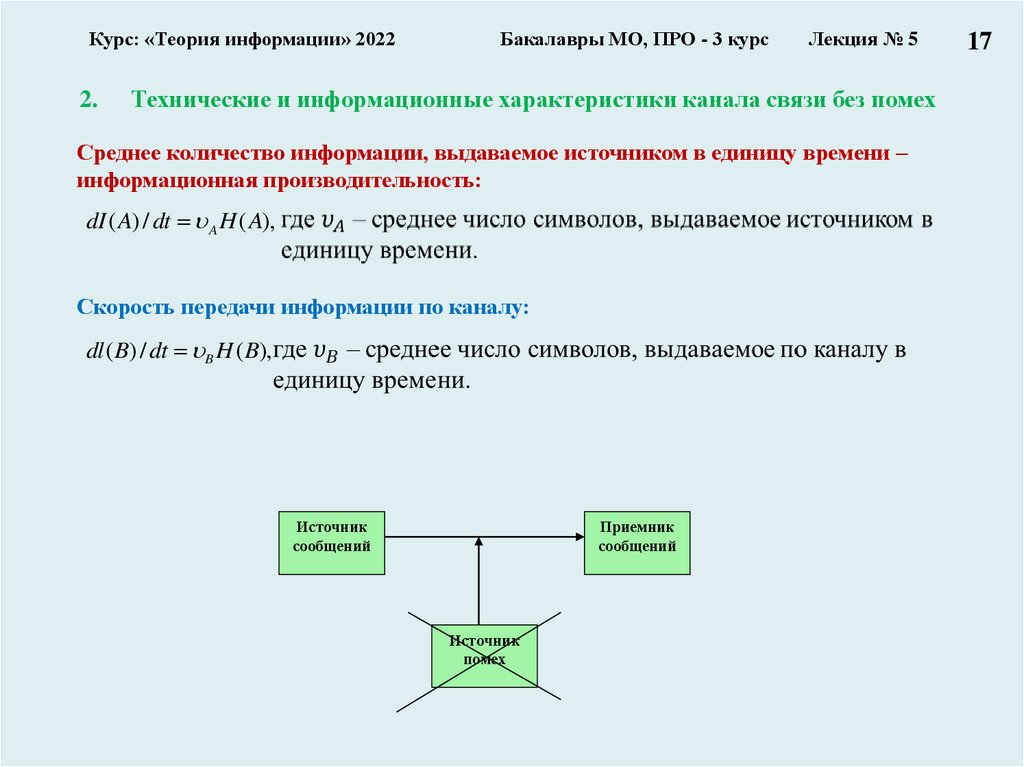
Технические и информационные характеристики канала связи без помех
Среднее количество информации, выдаваемое источником в единицу времени –
информационная производительность:
dI ( A) / dt A H ( A),
Скорость передачи информации по каналу:
dl ( B) / dt B H ( B),
Источник
сообщений
Приемник
сообщений
Источник
помех
17
18.
Курс: «Теория информации» 20222.
Бакалавры МО, ПРО - 3 курс
Лекция № 5
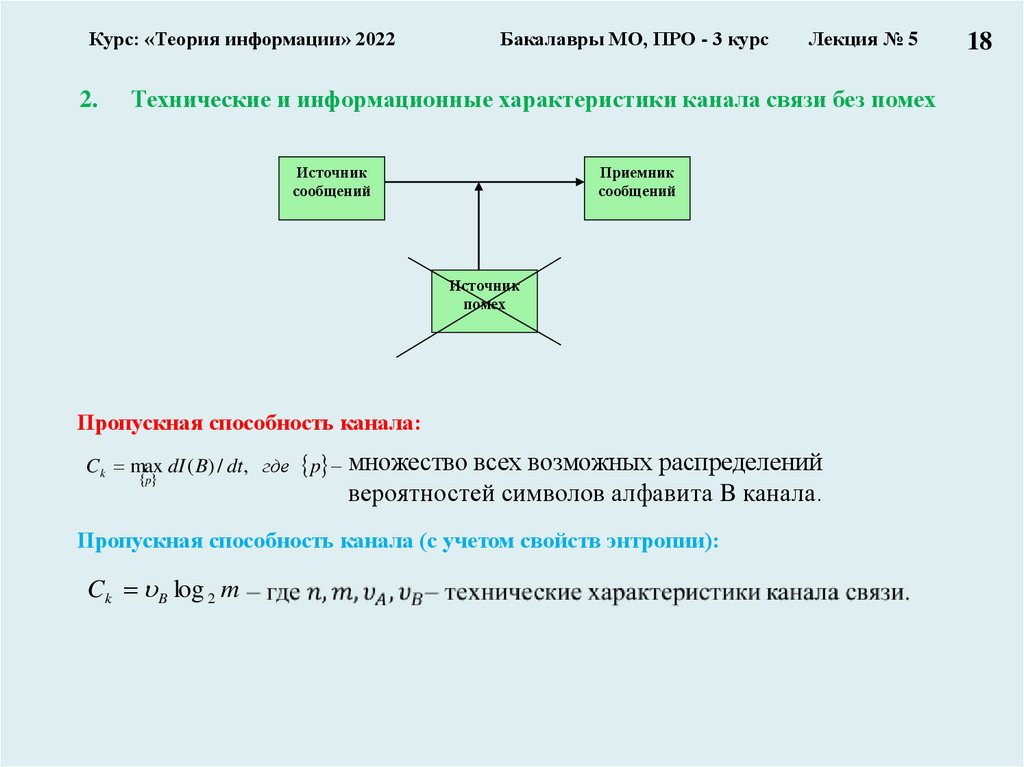
Технические и информационные характеристики канала связи без помех
Источник
сообщений
Приемник
сообщений
Источник
помех
Пропускная способность канала:
C k max dI ( B) / dt , где p множество всех возможных распределений
p
вероятностей символов алфавита B канала.
Пропускная способность канала (с учетом свойств энтропии):
Ck B log 2 m
18
19.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи
без помех
2.3. Обобщенные характеристики сигналов и каналов
19
20.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
20
3. Обобщенные характеристики сигналов и каналов
Сигнал может быть охарактеризован различными параметрами. Таких параметров, вообще
говоря, очень много, но для задач, которые приходится решать на практике, существенно
лишь небольшое их число. Например, при выборе прибора для контроля технологического
процесса может потребоваться знание дисперсии сигнала; если сигнал используется для
управления, существенным является его мощность и так далее.
Рассматривают три основных параметра сигнала, существенных для передачи информации
по каналу.
• время передачи сигнала
Tc
• мощность Pс сигнала,
передаваемого по
каналу с определенным
уровнем помех Pz
• спектр частот Fc
Чем больше значение Pс по сравнению с Pz,
тем меньше вероятность ошибочного приема.
Таким образом, представляет интерес
отношение Pс /Pz. Удобно пользоваться
логарифмом этого отношения, называемым
превышением сигнала над помехой:
Pc
L log a( )
c
Pz
21.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
21
3. Обобщенные характеристики сигналов и каналов
Эти три параметра позволяют представить любой сигнал в трехмерном пространстве с
координатами L, T, F в виде параллелепипеда с объемом Tc Fc Lc
Объем сигнала Vc
Vc Tc Fc Dc
Информационный канал характеризуется:
• временем использования канала Тк
• шириной полосы частот, пропускаемых каналом Fk
• динамическим диапазоном канала Dk характеризующим
его способность передавать различные уровни сигнала
Емкость канала Vk
Tk Tk Fk Dk
Неискаженная передача сигналов возможна только при условии, что сигнал по своему
объему «вмещается» в емкость канала.
Согласование сигнала с каналом передачи информации определяется соотношением
Vc Vk
22.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
3. Обобщенные характеристики сигналов и каналов
Однако соотношение выражает необходимое, но недостаточное
условие согласования сигнала с каналом. Достаточным условием
является согласование по всем параметрам:
Для информационного канала пользуются понятиями:
скорость ввода информации
скорость передачи информации
пропускная способность канала
Tc Tk
Fc Fk
Dc Dk
Скорость ввода информации (потоком информации) V(A) - среднее количество
информации, вводимое от источника сообщений в информационный канал в единицу
времени. Эта характеристика источника сообщений определяется только статистическими
свойствами сообщений.
Скорость передачи информации V(X,Y) – среднее количество информации,
передаваемое по каналу в единицу времени. Зависит от статистических свойств
передаваемого сигнала и от свойств канала.
Пропускная способность С – наибольшая теоретически достижимая для данного
канала скорость передачи информации. Характеристика канала не зависит от статистики
сигнала.
22
23.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
3. Обобщенные характеристики сигналов и каналов
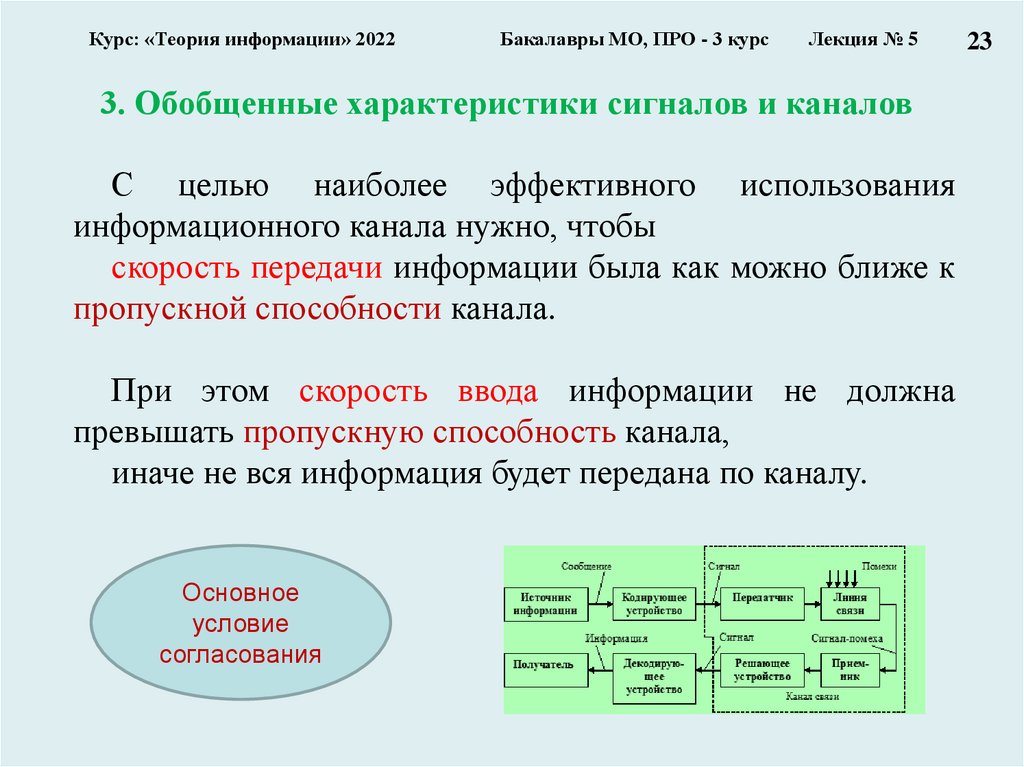
С целью наиболее эффективного использования
информационного канала нужно, чтобы
скорость передачи информации была как можно ближе к
пропускной способности канала.
При этом скорость ввода информации не должна
превышать пропускную способность канала,
иначе не вся информация будет передана по каналу.
Основное
условие
согласования
23
24.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
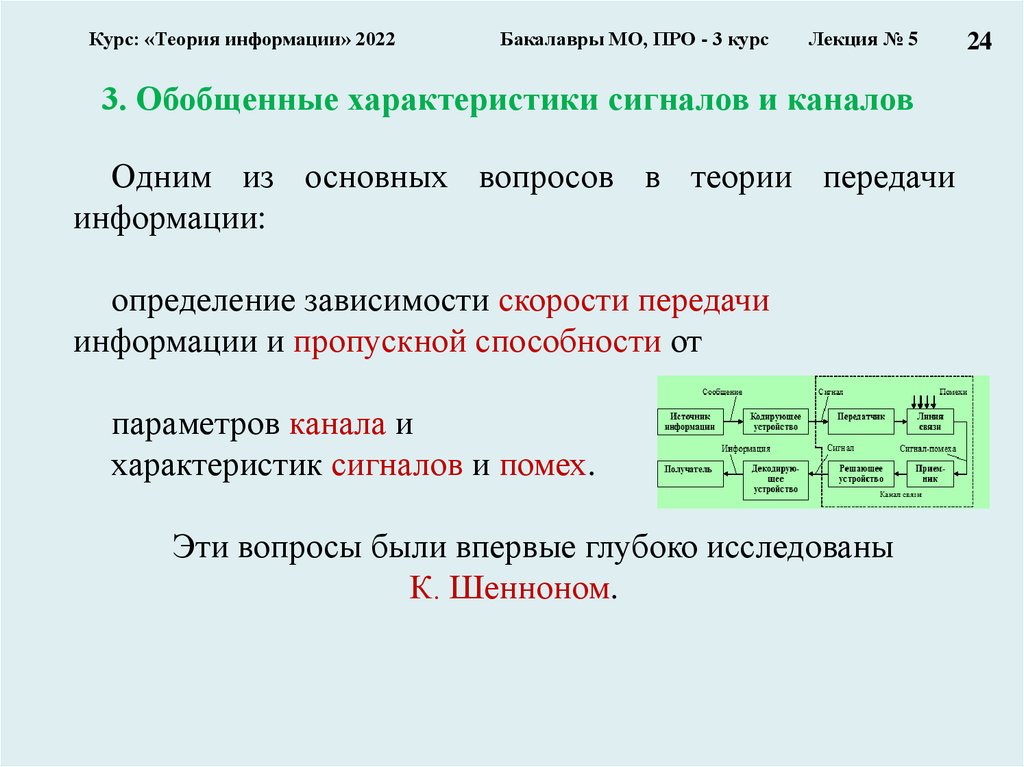
3. Обобщенные характеристики сигналов и каналов
Одним из основных вопросов в теории передачи
информации:
определение зависимости скорости передачи
информации и пропускной способности от
параметров канала и
характеристик сигналов и помех.
Эти вопросы были впервые глубоко исследованы
К. Шенноном.
24
25.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
Лекция № 5
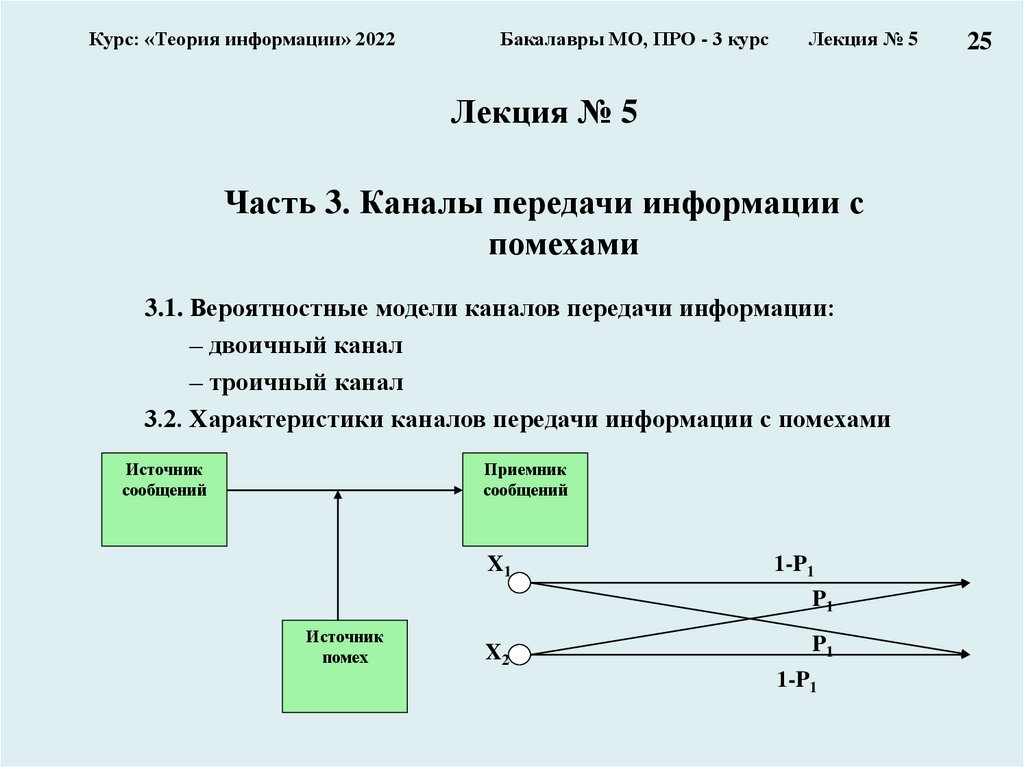
Часть 3. Каналы передачи информации с
помехами
3.1. Вероятностные модели каналов передачи информации:
– двоичный канал
– троичный канал
3.2. Характеристики каналов передачи информации с помехами
Источник
сообщений
Приемник
сообщений
X1
1-P1
P1
Источник
помех
X2
P1
1-P1
25
26.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
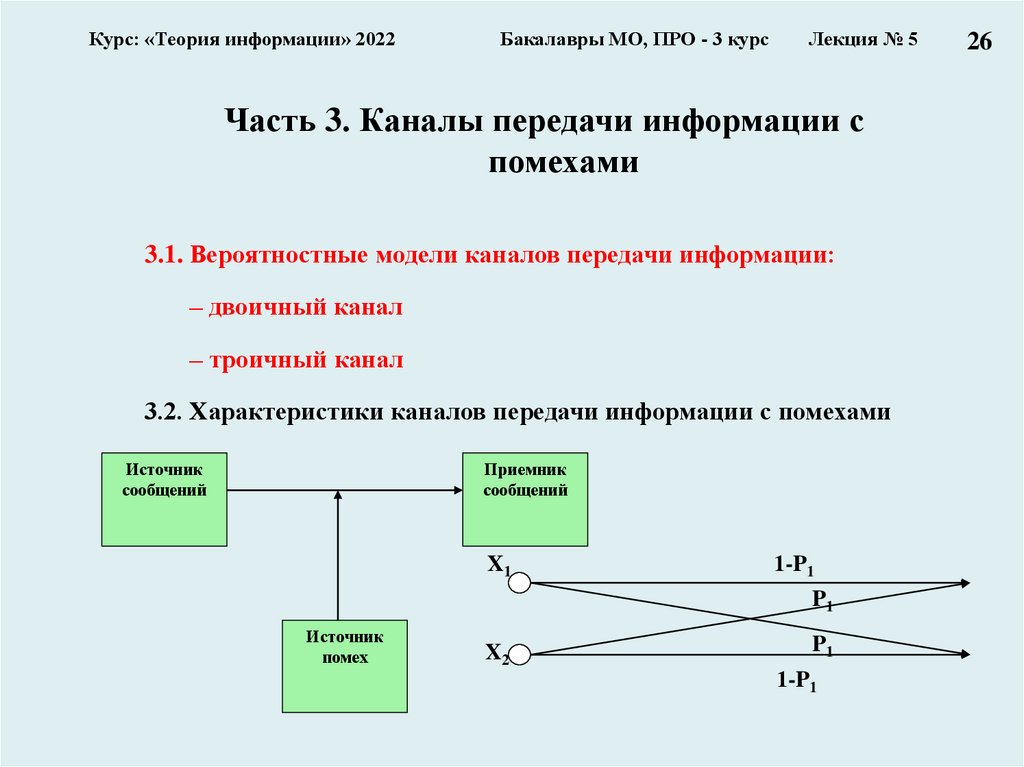
Часть 3. Каналы передачи информации с
помехами
3.1. Вероятностные модели каналов передачи информации:
– двоичный канал
– троичный канал
3.2. Характеристики каналов передачи информации с помехами
Источник
сообщений
Приемник
сообщений
X1
1-P1
P1
Источник
помех
X2
P1
1-P1
26
27.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
27
5.1 Вероятностные модели каналов передачи информации
Двоичный канал
Пример 1. По двоичному каналу связи с помехами
передаются две цифры 1 и 0 с вероятностями p1 = p2 = 0,5.
Вероятность перехода единицы в единицу и нуля в нуль
соответственно равны p(1/1) = p, p(0/0) = q.
Определить закон распределения вероятностей случайной
величины ξ – однозначного числа, получаемого на приемной
стороне.
28.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
28
5.1 Вероятностные модели каналов передачи информации
Двоичный канал
Решение. ξ X = {0, 1}. Нуль (ξ = 0) на приемной стороне
может быть получен в двух случаях: при передаче нуля или
при передаче единицы. Следовательно, по формуле полной
вероятности
P (0) P(0,0) P(1,0) P(0) P(0 / 0) P(1) P(0 / 1),
P(0 / 1) 1 P(1 / 1).
29.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
5.1 Вероятностные модели каналов передачи информации
Двоичный канал
Поэтому
P (0) 0,5q 0,5(1 p) 0,5(1 q p).
, ) 0,5(1 q p).
Аналогично P (1) P (0,1) P (11
Распределение вероятностей представлено в табл.
xi
0
1
pi
0,5(10p + q)
0,5(1 ‒ p + q)
29
30.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
30
5.1 Вероятностные модели каналов передачи информации
Троичный канал
Пример 1. Дана матрица
1
8
1
P( X , Y )
8
1
8
1 1
8 8
1
0
, X , Y
8
1 1
8 8
Определить: распределения вероятностей на входе и на выходе канала,
условное распределение вероятностей появления сигналов на выходе
канала при фиксированном входе и на входе канала при фиксированном
выходе канала.
31.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
5.1 Вероятностные модели каналов передачи информации
Троичный канал
Решение. По формуле полной вероятности имеем:
3
P ( x1 ) p ( x1 , y j )
j 1
3
,
8
3
1
3
3
P ( x 2 ) , P ( x 3 ) , P ( y1 ) p ( x i , y1 ) ,
8
4
8
i 1
P(y2 )
1
,
4
P(y3 )
По теореме умножения
1
p ( x 1 / y 1 ) p ( x 1 y 1 ) / p ( y1 ) ,
3
1
p( x1 / y 2 ) ,
2
p( x 1 / y 3 )
1
,
3
p ( x 2 / y1 )
1
,
3
p( x 2 / y 2 ) 0,
p( x 2 / y 3 )
1
,
3
p ( x 3 / y1 )
1
,
3
p( x 3 / y 2 )
1
,
2
p( x 3 / y 3 )
1
.
2
3
.
8
31
32.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
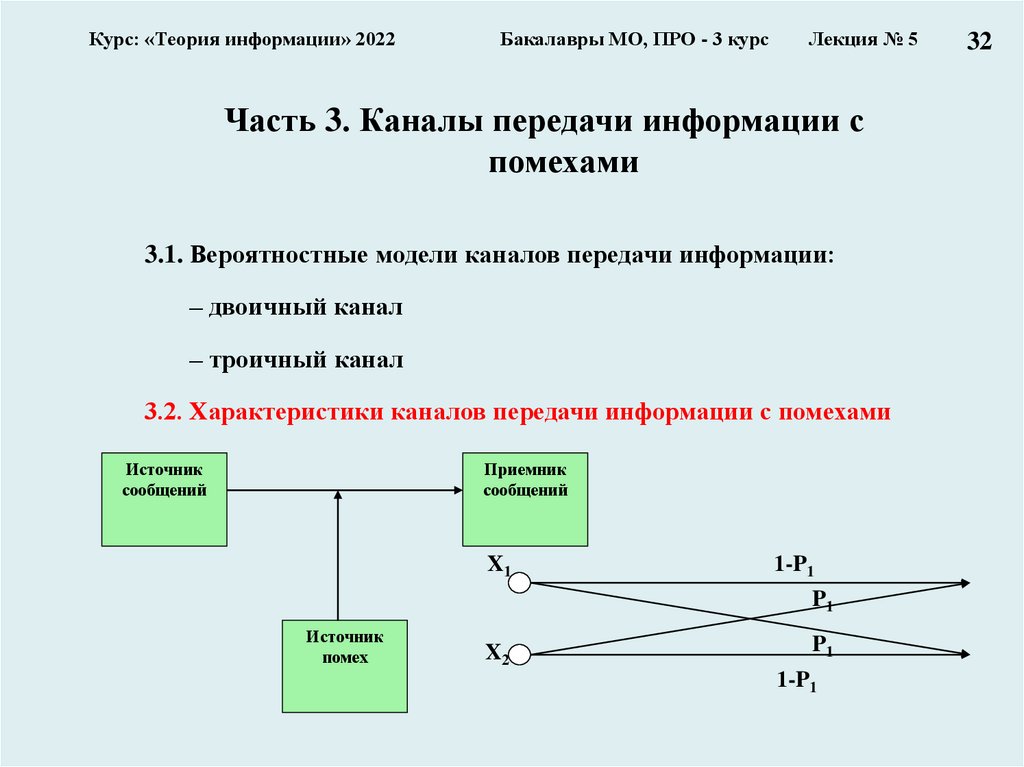
Часть 3. Каналы передачи информации с
помехами
3.1. Вероятностные модели каналов передачи информации:
– двоичный канал
– троичный канал
3.2. Характеристики каналов передачи информации с помехами
Источник
сообщений
Приемник
сообщений
X1
1-P1
P1
Источник
помех
X2
P1
1-P1
32
33.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
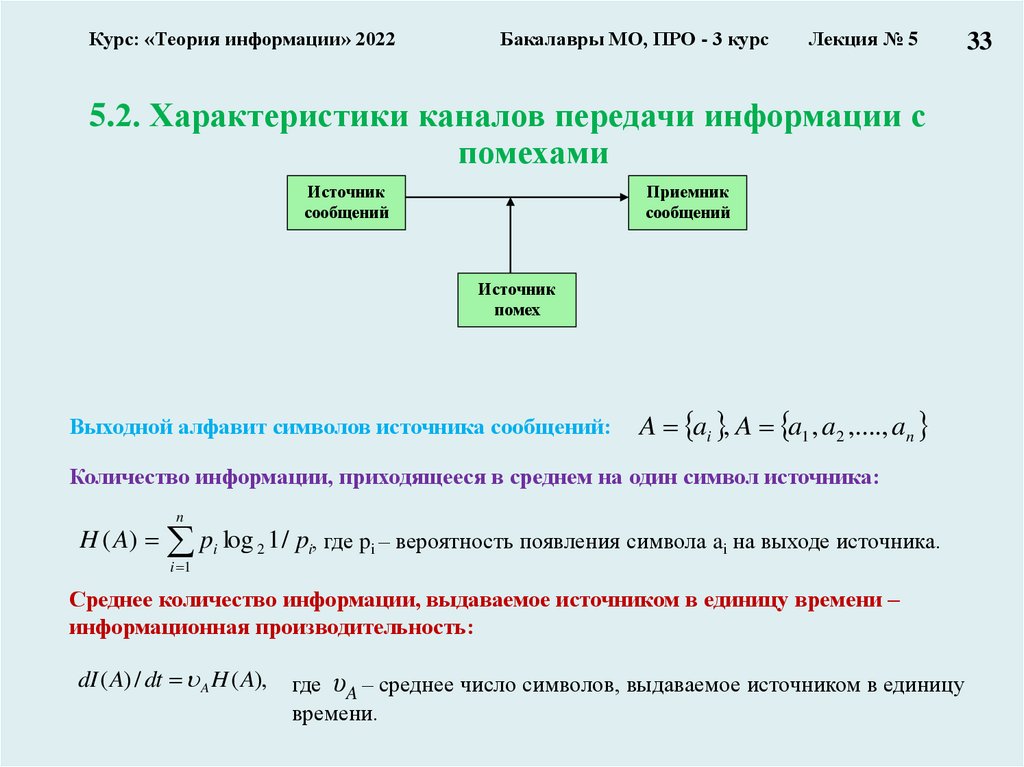
5.2. Характеристики каналов передачи информации с
помехами
Источник
сообщений
Приемник
сообщений
Источник
помех
Выходной алфавит символов источника сообщений:
A ai , A a1 , a2 ,...., an
Количество информации, приходящееся в среднем на один символ источника:
n
H ( A) pi log 2 1 / pi, где pi – вероятность появления символа ai на выходе источника.
i 1
Среднее количество информации, выдаваемое источником в единицу времени –
информационная производительность:
dI ( A) / dt A H ( A),
где υA – среднее число символов, выдаваемое источником в единицу
времени.
33
34.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
34
5.2. Характеристики каналов передачи информации с
помехами
Алфавиты символов канала связи:
Bвх X x1 , x2 ,..., xm , Bвых Y y1 , y2 ,..., yl
Матрица переходных вероятностей:
l
p( yi / xk ) , где k 1...m, i 1...l ; p( yi / xk ) 1
i 1
Среднее количество информации на один входной и на один выходной
символ канала:
m
l
i 1
j 1
H ( X ) p( xi ) log 2 1 / p( xi ); H (Y ) p( y j ) log 2 1 / p( y j )
35.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
35
5.2. Характеристики каналов передачи информации с
помехами
Информация, которую несет выход канала о входе:
I (Y , X ) H ( X ) H y ( X ) H (Y ) H x (Y )
где Hy(X) – ненадежность канала, Hx(Y) – энтропия шума.
Скорость передачи информации по каналу:
dl ( B) / dt B I ( X ,Y ),
где υB – среднее число символов, выдаваемое каналом в единицу времени.
Пропускная способность канала:
C k max dI ( B) / dt , где p множество всех возможных распределений
p
вероятностей входного алфавита символов канала
C k B max I ( x, y ) n, m, l , A , B
– {p} характеристики канала.
36.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
5.2. Характеристики каналов передачи информации с
помехами
ПРИМЕР
1. Найти пропускную способность двоичного симметричного канала – канала с
двухсимвольными входными и выходными алфавитами и одинаковыми
вероятностями ошибок (см. рисунок)
X1
1-P1
P1
P1
X2
1-P1
если априорные вероятности появления входных символов
p( x1 ) p1 p, p( x2 ) p2 1 p
36
37.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
5.2. Характеристики каналов передачи информации с
помехами
РЕШЕНИЕ. В соответствии с моделью канала условные вероятности
y
y
y
y
p ( 1 ) p( 2 ) pl , p ( 1 ) p ( 2 ) 1 pl
x2
x1
x1
x2
Пропускная способность канала
Найдем энтропию шума
Ck B max H (Y ) H (Y / X )
p
2
2
H ( X / Y ) p( xi y j ) log 2 1 / p( y j / xi )
i 1 j 1
По теореме умножения
следовательно,
p ( y j , xi ) p ( xi ) p ( y j / xi )
p( x1 y1 ) p(1 pl )
p( x 2 y1 ) (1 p) pl
p( x1 y1 ) ppl
p( x 2 y 2 ) (1 p)(1 pl )
Подставляя в формулу, получаем H (Y / X ) pl log 2 1 / pl (1 pl ) log 2 1 /(1 pl )
Таким образом, H(Y/X) не зависит от распределения входного алфавита, следовательно,
Ck k max H (Y ) н H (Y / X )
p
37
38.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 5
38
5.2. Характеристики каналов передачи информации с
помехами
Определим энтропию выхода
H (Y ) p ( y1 log 2 )1 / p ( y1 ) p ( y 2 ) log 2 1 / p ( y 2 ),
где p( y1 ) p ( y1 x1 ) p ( y1 x 2 ) p (1 pl ) pl (1 p );
p( y 2 ) p ( y 2 x1 ) p ( y 2 x 2 ) ppl (1 p )(1 pl )
Таким образом,
H (Y ) p(1 pl ) pl (1 p) log 2 1 / p(1 pl ) pl (1 p) ppl (1 p)(1 pl )
log 2 1 / ppl (1 p)(1 pl )
Варьируя p, убеждаемся, что максимальное значение H/Y, равное I, получается при
равновероятных входных символах p(y1) и p(y2).
Следовательно,
Ck k 1 pl log 2 1 / pl (1 pl ) log 2 1 /(1 pl ) .
39.
Курс: «Теория информации» 2022Заключение!!!
Бакалавры МО, ПРО - 3 курс
Лекция № 5
Лекция № 5
Часть 1. Условная энтропия и взаимная информация
1.1. Условная энтропия
1.2. Взаимная информация
1.3. Пример с троичным каналом
Часть 2. Каналы передачи информации
2.1. Структурная схема системы передачи информации (повторение)
2.2. Технические и информационные характеристики канала связи без помех
2.3. Обобщенные характеристики сигналов и каналов
Часть 3. Каналы передачи информации с помехами
3.1. Вероятностные модели каналов передачи информации:
– двоичный канал
– троичный канал
3.2. Характеристики каналов передачи информации с помехами
1
40.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
Часть 1. Результаты Шеннона и проблемы
кодирования
1. Теорема Шеннона для канала без помех
2. Теорема Шеннона для канала с помехами
3. Значение результатов Шеннона для задач передачи,
хранения и поиска информации
4. Современные технические средства передачи информации
1
41.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
Часть 1. Результаты Шеннона и проблемы
кодирования
1. Теорема Шеннона для канала без помех
2. Теорема Шеннона для канала с помехами
3. Значение результатов Шеннона для задач
передачи, хранения и поиска информации
4. Современные технические средства передачи
информации
1
42.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
1. Теорема Шеннона для канала без помех
! Две фундаментальные теоремы идеального кодирования,
носящие имя Шеннона:
первая из них рассматривает случай
отсутствия помех в канале,
вторая учитывает наличие помех,
приводящих к ошибкам.
Проблема согласования источника сообщений и канала при
передаче сообщений. ?
2
43.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
1. Теорема Шеннона для канала без помех
Пусть:
• источник сообщений выдает сообщения с некоторой
скоростью υu (сообщений/ед. времени),
— техническая производительность источника.
• по каналу можно передавать без искажений сообщения со
скоростью, не превышающей некоторую величину υk
(сообщений/ед. времени),
— техническая пропускная способность канала.
2
44.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
1. Теорема Шеннона для канала без помех
Если выполняется условие
υu<υk,
то канал успевает передать все сообщения, поступающие на
его вход от источника, и передача будет вестись без
искажений.
Что произойдет, если υu>υk?
Можно ли в этом случае обеспечить передачу без
искажений?
2
45.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
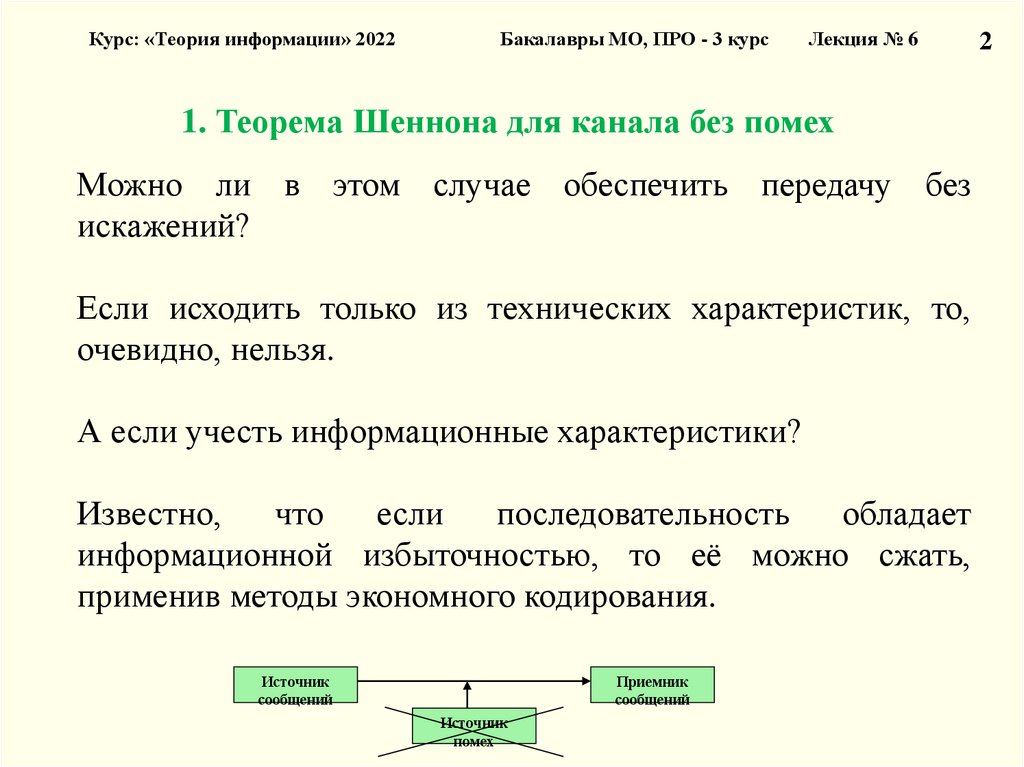
1. Теорема Шеннона для канала без помех
Можно ли в этом случае обеспечить передачу без
искажений?
Если исходить только из технических характеристик, то,
очевидно, нельзя.
А если учесть информационные характеристики?
Известно,
что
если
последовательность
обладает
информационной избыточностью, то её можно сжать,
применив методы экономного кодирования.
Источник
сообщений
Приемник
сообщений
Источник
помех
2
46.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
2
1. Теорема Шеннона для канала без помех
1)0 H ( ) log 2 N ;
2) N 2, p1 p2 0,5, H ( ) 1;
3) H ( , ) H ( ) H ( ),
если ξ и η – независимы
1 H ( A) / max H ( A) 1 H ( A) / log 2 N
N
M
H (Y / X ) p( xi y j ) log 2
i 1 j 1
1
p( y j / xi )
I ( , ) H ( ) H ( ).
.
47.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
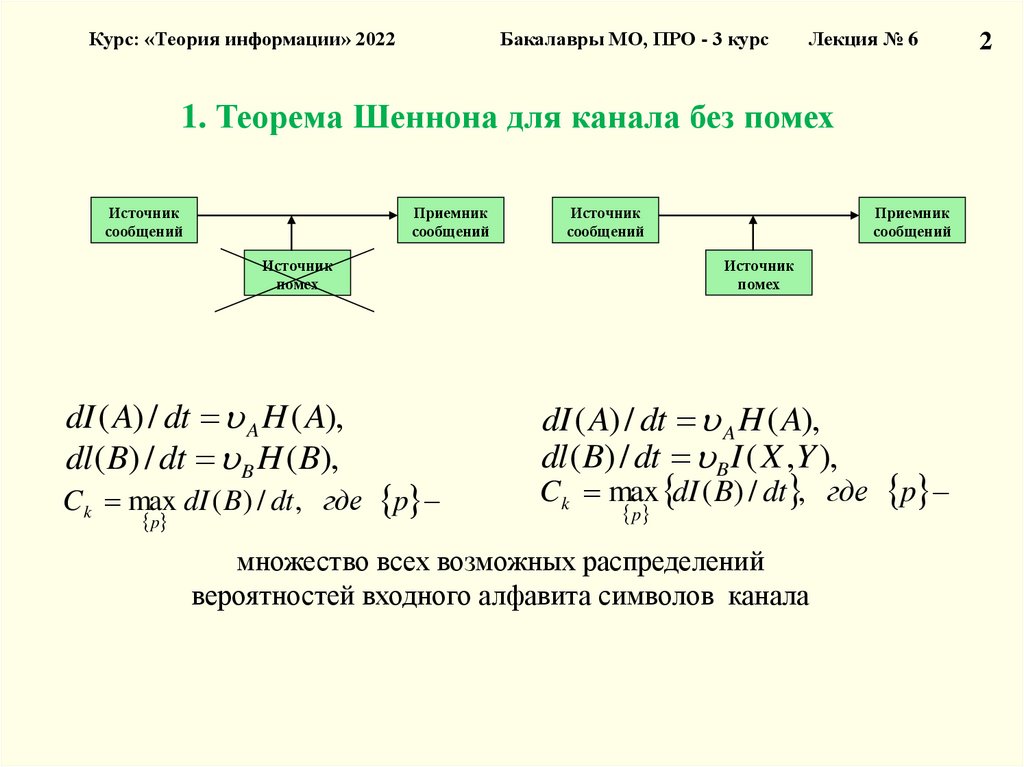
1. Теорема Шеннона для канала без помех
Источник
сообщений
Приемник
сообщений
Источник
сообщений
Источник
помех
Источник
помех
dI ( A) / dt A H ( A),
dl ( B) / dt B H ( B),
C k max dI ( B) / dt , где p
p
Приемник
сообщений
dI ( A) / dt A H ( A),
dl ( B) / dt B I ( X ,Y ),
C k max dI ( B) / dt , где p
p
множество всех возможных распределений
вероятностей входного алфавита символов канала
2
48.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
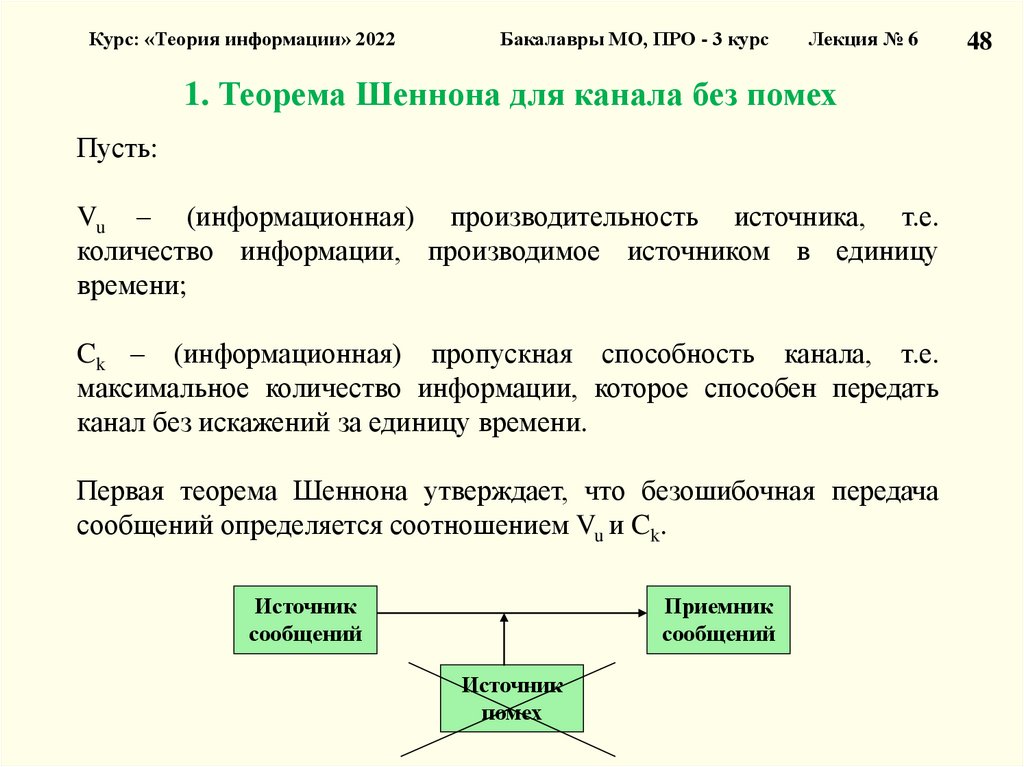
1. Теорема Шеннона для канала без помех
Пусть:
Vu – (информационная) производительность источника, т.е.
количество информации, производимое источником в единицу
времени;
Ck – (информационная) пропускная способность канала, т.е.
максимальное количество информации, которое способен передать
канал без искажений за единицу времени.
Первая теорема Шеннона утверждает, что безошибочная передача
сообщений определяется соотношением Vu и Ck.
Источник
сообщений
Приемник
сообщений
Источник
помех
48
49.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
49
1. Теорема Шеннона для канала без помех
Первая теорема Шеннона: если пропускная способность
канала без помех превышает производительность источника
сообщений, т.е. удовлетворяется условие
Ck >Vu,
то существует способ кодирования и декодирования
сообщений источника, обеспечивающий сколь угодно
высокую надежность передачи сообщений. В противном
случае, т.е. если
Ck <Vu
Такого способа нет.
50.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
50
1. Теорема Шеннона для канала без помех
Идеальное кодирование по Шеннону по существу
представляет собой экономное кодирование
последовательности сообщений при безграничном
укрупнении сообщений. Такой способ кодирования
характеризуется задержкой сообщений
2T ,
поскольку
кодирование
очередной
типичной
последовательности может начаться только после
получения последовательности источника длительностью
T,
а
декодирование
–
только
когда
принята
последовательность из канала той же длительности T.
51.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
1. Теорема Шеннона для канала без помех
Поскольку требуется T→∞, то идеальное кодирование
требует бесконечной задержки передачи информации.
В этом причина технической нереализуемости идеального
кодирования по Шеннону.
Тем
не
менее,
значение
этого
результата,
устанавливающего
предельные
соотношения
информационных характеристик источника и канала для
безошибочной передачи сообщений, весьма велико.
Исторически именно теорема Шеннона инициировала и
определила развитие практических методов экономного
кодирования.
51
52.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
Лекция № 6
Часть 1. Результаты Шеннона и проблемы
кодирования
1. Теорема Шеннона для канала без помех
2. Теорема Шеннона для канала с помехами
3. Значение результатов Шеннона для задач передачи,
хранения и поиска информации
4. Современные технические средства передачи информации
Источник
сообщений
Приемник
сообщений
Источник
помех
1
53.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
2. Теорема Шеннона для канала с помехами
При отсутствии помех ошибки при передаче могут
возникать только за счет неоднозначного кодирования
сообщений.
Рассмотрим теперь ситуацию, когда в канале действуют
помехи, вызывающие искажения передаваемых символов.
Возникающие при этом ошибки носят случайный
характер, они действуют при любой скорости передачи
сообщений через канал, в том числе, когда
Vu<Vk.
53
54.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
2. Теорема Шеннона для канала с помехами
Возможен ли такой способ кодирования, при котором
сообщения передаются через канал без ошибок с
некоторой ненулевой скоростью Vk≠0 (действие ошибок
полностью устраняется при кодировании)?
Методы помехоустойчивого кодирования основаны на
введении избыточности.
Для полного устранения ошибок их применение требует
введения бесконечной избыточности.
Это может привести к снижению скорости передачи
сообщений до нуля.
54
55.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
2. Теорема Шеннона для канала с помехами
Вторая теорема Шеннона утверждает, что такой способ
возможен.
Тогда возникает следующий вопрос: чем определяется
максимальная скорость передачи сообщений по каналу с
помехами?
Оказывается, что, как и для канала без помех, она
определяется
соотношением
информационных
характеристик источника и канала.
Источник
сообщений
Приемник
сообщений
Источник
помех
55
56.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
56
2. Теорема Шеннона для канала с помехами
Вторая теорема Шеннона:
Для канала с помехами существует такой способ
кодирования, при котором обеспечивается безошибочная
передача всех сообщений источника, если только
пропускная
способность
канала
превышает
производительность источника
Ck>Vu.
dI ( A) / dt A H ( A),
Источник
сообщений
Приемник
сообщений
Источник
помех
C k max dI ( B) / dt , где p
p
множество всех возможных распределений
вероятностей входного алфавита символов канала
57.
Курс: «Теория информации» 2022Бакалавры МО, ПРО - 3 курс
Лекция № 6
2. Теорема Шеннона для канала с помехами
Возникающая ситуация поясняется на рис. 1.
На вход канала поступают типичные
последовательности источника АТ.
Они кодируются последовательностями




































































































 informatics
informatics








