Similar presentations:
Теория информации. Теорема кодирования
1.
Теория информацииТеорема кодирования
1
Лекция 7. Теорема кодирования
2. Теория информации
Задача − представление сообщений иззаданного
дискретного
множества
последовательностью символов, принадлежащих
заданному алфавиту.
Цель − конструирование последовательностей
символов, минимизирующих среднее число
символов, приходящихся на одно сообщение по
ансамблю
статистически
независимых
сообщений.
Лекция 7. Теорема кодирования
3. Теория информации
Нижняя граница для средней длины кодовогослова
U − ансамбль из M сообщений u1 , u 2 ,...,u k ,...,u M с
соответствующими вероятностями P u k .
D − число символов в алфавите.
n k – число символов в кодовом слове,
соответствующем сообщению u k .
Среднее число символов на одно сообщение:
M
n P u k nk
k 1
Найдем нижнюю границу для n .
Лекция 7. Теорема кодирования
4. Теория информации
Нижняя граница для средней длины кодовогослова
I X M I xk P x log P x H X
X
1
H X log M при P u k
M
log D − пропускная способность кодового алфавита
H Y X H Y
H U
n
n log D H U
log D
Лекция 7. Теорема кодирования
5. Теория информации
Общие правила конструирования кодовых словсо средней длиной, достаточно близкой к
нижней границе по Шеннону
1. В каждой из позиций кодового слова
различные
символы
алфавита
должны
использоваться с равными вероятностями, с тем
чтобы максимизировать среднее количество
информации, доставляемое ими.
2. Вероятности появления символов в каждой
позиции кодового слова должны не зависеть от
всех предыдущих символов.
Лекция 7. Теорема кодирования
6. Теория информации
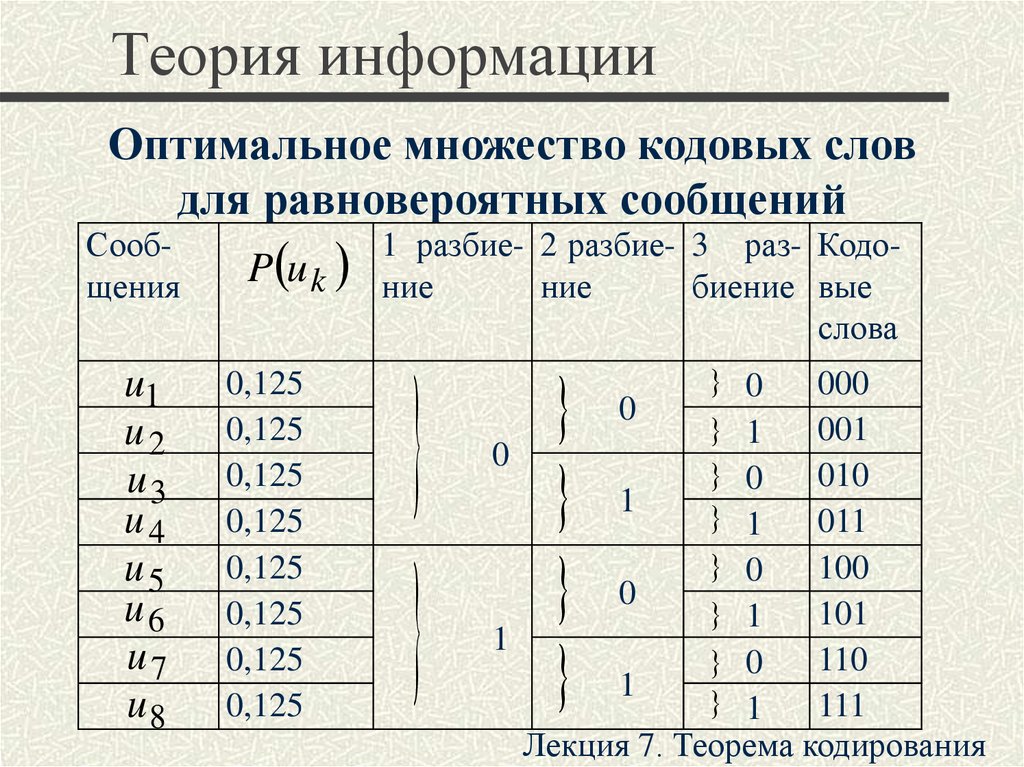
Оптимальное множество кодовых словдля равновероятных сообщений
Сообщения
u1
u2
u3
u4
u5
u6
u7
u8
P u k
0,125
0,125
0,125
0,125
0,125
0,125
0,125
0,125
1 разбие- 2 разбие- 3 раз- Кодоние
ние
биение вые
слова
0
1
0
1
000
0
001
0
010
1
011
0
100
0
1
101
1
110
0
1
1
111
Лекция 7. Теорема кодирования
7. Теория информации
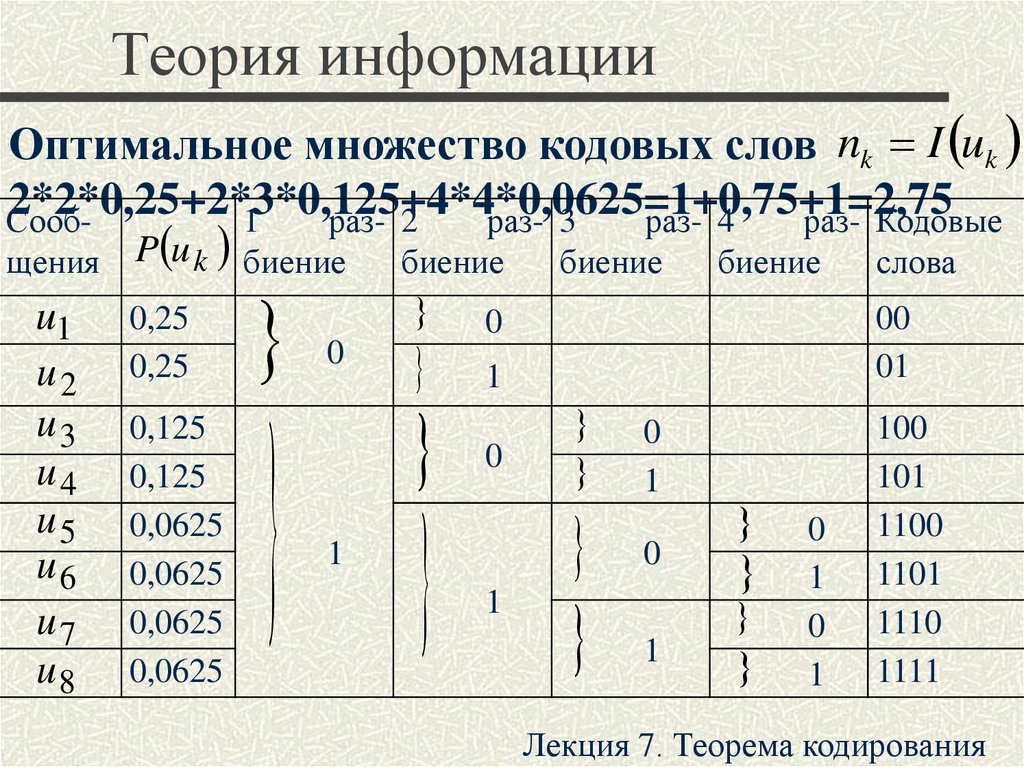
Оптимальное множество кодовых слов nk I uk2*2*0,25+2*3*0,125+4*4*0,0625=1+0,75+1=2,75
Сооб1
раз- 2
раз- 3
раз- 4
раз- Кодовые
щения
u1
u2
u3
u4
u5
u6
u7
u8
P u k биение
0,25
0,25
0,125
0,125
0,0625
0,0625
0,0625
0,0625
биение
0
1
биение
биение
00
01
0
1
0
1
слова
0
1
0
1
0
1
0
1
100
101
1100
1101
1110
1111
Лекция 7. Теорема кодирования
8. Теория информации
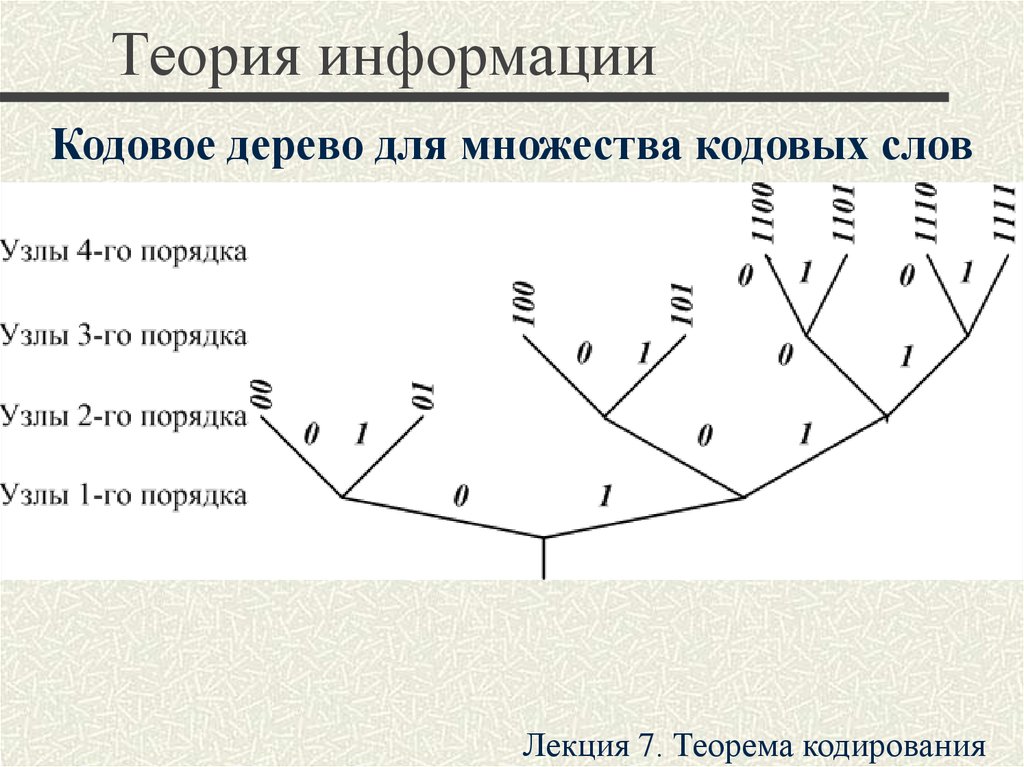
Кодовое дерево для множества кодовых словЛекция 7. Теорема кодирования
9. Теория информации
Кодовое дерево для множества кодовых словСообщения могут быть сопоставлены только
концевым узлам, иначе алфавит становится
троичным (0, 1, остановка). Кодовое слово совокупность указаний для достижения узла,
соответствующего сообщению. Ни одно из
кодовых слов не совпало с началом (префиксом)
какого-либо более длинного кодового слова. Иначе
при непрерывной передаче сообщений невозможно
однозначно разбить последовательность символов
на последовательные сообщения.
Лекция 7. Теорема кодирования
10. Теория информации
Неравенство КрафтаM
nk
D
1
Теорема. Неравенство k 1
является необходимым и достаточным условием
существования кодовых слов, соответствующих
концевым узлам дерева с длинами, равными n k .
Доказательство. Покажем сначала, что это
соотношение необходимо.
Из каждого узла дерева исходит не более D ветвей.
Отсюда следует, что может быть не более D n узлов
порядка n .
Лекция 7. Теорема кодирования
11. Теория информации
Неравенство КрафтаНаличие концевого узла порядка n k (не большего,
чем n) исключает D n nk возможных узлов порядкаn
M
D
n nk
k 1
M
D
n
nk
D
1
k 1
Необходимость условия теоремы доказана.
Лекция 7. Теорема кодирования
12. Теория информации
Неравенство КрафтаДля доказательства достаточности условия
необходимо показать, что дерево с концевыми
узлами, т. е. множество кодовых слов с заданными
длинами, может быть фактически построено.
Пусть nk nk 1 .
Предположим, что удалось построить дерево,
содержащее все заданные концевые узлы порядка,
меньшего m, и что дерево должно содержать m
концевых узлов порядка m . Согласно условию
j
D
k 1
nk
m D
m
M
nk
1
D
k j 1Лекция 7. Теорема кодирования
13. Теория информации
Неравенство Крафтаj
D
nk
k 1
m D
m
M
D
nk
1
k j
m 1
nk m
nk m
j – число концевых узлов порядка, меньшего чем m
j
M
D D m D D D D D
1
k j m 1
k
m
nk
m
m
m
nk m
nk
m
nk m
j
m D D
m
k 1
m nk
M
D
m nk
k j m 1
Лекция 7. Теорема кодирования
14. Теория информации
Неравенство Крафтаj
m D m D m n
k
k 1
M
m nk
D
k j m 1
j – число концевых узлов порядка, меньшего чем m
j
Число доступных узлов порядка m : D D
k 1
Отсюда следует, что число доступных узлов
порядка m не меньше заданного числа концевых
узлов того же порядка, а потому все они могут
быть включены в дерево. Что и требовалось
Лекция 7. Теорема кодирования
доказать.
m
m nk
15. Теория информации
Дерево, содержащее M концевых узлов порядкаn1 , n2 ,...,n M может иметь или не иметь еще
добавочные концевые узлы. Заданное множество
концевых узлов называется полным, если
существует дерево, имеющее эти концевые узлы и
не имеющее никаких других концевых узлов (т.е.
если соответствующее дерево не может быть
дополнено никакими узлами), т. е., другими
словами, если заданное множество узлов целиком
заполняет дерево.
Лекция 7. Теорема кодирования
16. Теория информации
MТеорема. Равенство D nk 1
k 1
является необходимым и достаточным условием
того, чтобы заданное множество концевых узлов
было полным.
Теорема. Равенство M D 1 1 ,
где
– целое положительное число, является
необходимым
и
достаточным
условием
существования дерева с полным множеством из M
концевых узлов.
Лекция 7. Теорема кодирования
17. Теория информации
Доказательство.M i – число имеющихся в дереве свободных узлов,
когда дерево построено вплоть до порядка i
m i – число промежуточных узлов порядка i, когда
дерево построено до узлов порядка более
высокого, чем i .
M 2 M1 m1 m1D
M 1 D D 1 1
M1 m1 D 1
M i 1 M i mi D 1
nM 1
M 1 D 1 1 mi
i 1
Необходимость условия доказана.
Лекция 7. Теорема кодирования
18. Теория информации
Основная теорема кодированияТеорема. При заданном ансамбле U из M
сообщений с энтропией H U и алфавитом,
состоящим
из D символов,
возможно
так
закодировать сообщения ансамбля посредством
последовательностей символов, принадлежащих
заданному алфавиту, что среднее число символов
на сообщение удовлетворяет неравенству
H U
H U .
(1)
log D
n
log D
1
Число n не может быть сделано меньше, чем
Лекция
7. Теорема кодирования
нижняя граница в выражении
(1).
19. Теория информации
Основная теорема кодированияВывод нижней границы n M
P u k n k
k 1
H U n log D 0
Пусть Q D nk n k log D log Qk
k
M
M
k 1
k 1
H U n log D P u k log P uk P uk nk log D
M
M
k 1
k 1
P u k log P u k P u k log Qk
Qk
Qk M
P uk log
1 log e
P uk
P uk k 1
k 1
P uk
M
M nk
D 1 log e 1 1 log e 0
Лекция 7. Теорема кодирования
k 1
20. Теория информации
Вывод верхней границы.Лемма. Для существования множества кодовых
слов со средней длиной
H U
n
log D
необходимо и достаточно, чтобы для каждого
сообщения выполнялось условие
I u k log P u k
a
, где a - целое число.
log D
log D
Когда это условие выполнено,
I u k
nk
log D
Лекция 7. Теорема кодирования
21. Теория информации
Вывод верхней границы.I u k
* I u k
nk
1
log D
log D
M
I uk
I uk M
*
P uk
P uk nk P uk
1
log D k 1
k 1
k 1
log D
M
H U
H U
n
1
log D
log D
Лекция 7. Теорема кодирования
22. Теория информации
Источники статистически независимыхсообщений
Теорема. При любом заданном как угодно малом
положительном числе можно найти натуральное
число и соответствующее множествоM кодовых
слов, такое, что среднее число символов на
сообщение удовлетворяет неравенству
H U
n
.
log D
Обратно, невозможно найти натуральное число и
соответствующее множество кодовых слов, такое,
H U
что
n
log D
Лекция 7. Теорема кодирования
23. Теория информации
Источники статистически независимыхсообщений
Доказательство.
H U
H U 1
1
n
;
n
1;
log D
log D
log D
log D
H U
H U
Когда
каждое
сообщение
статистически
независимо от всех предыдущих сообщений, то
кодирование
последовательности
сообщений
вместо отдельных сообщений может уменьшить
среднее число символов на сообщение не более
Лекция 7. Теорема кодирования
чем на один символ.
24. Теория информации
Метод оптимального кодирования ХафманаЭтот метод всегда приводит к получению
оптимального множества кодовых слов в том
смысле, что никакое другое множество не имеет
меньшего среднего числа символов на
сообщение.
1-й шаг.M сообщений располагаются в порядке
убывания вероятностей.
2-й
шаг.
Пусть m o –
целое
число,
удовлетворяющее двум требованиям
2 mo D , M mo a, где a - целое положительное
D 1
Лекция 7. Теорема кодирования
число.
25. Теория информации
Метод оптимального кодирования ХафманаГруппируем вместе m o сообщений, имеющих
наименьшие вероятности, и вычисляем общую
вероятность такого подмножества сообщений.
3-й шаг. Из первоначального ансамбля образуем
вспомогательный
ансамбль
сообщений,
рассматривая подмножество из
сообщений,
образованных на 2-м шаге, как отдельное
сообщение с вероятностью, равной вероятности
всего
подмножества.
Вновь
располагаем
сообщения этого вспомогательного ансамбля в
Лекция 7. Теорема кодирования
порядке убывания вероятностей.
26. Теория информации
Метод оптимального кодирования Хафмана4-й шаг. Образуем подмножество из D
сообщений вспомогательного ансамбля, имеющих
наименьшие вероятности, и вычисляем их общую
вероятность.
5-й шаг. Из первого вспомогательного ансамбля
образуем второй вспомогательный ансамбль,
рассматривая подмножество из
сообщений,
образованное на четвертом шаге, как отдельное
сообщение с вероятностью, равной общей
вероятности всего подмножества. Располагаем
сообщения этого второго вспомогательного
ансамбля в порядке убывания
вероятностей.
Лекция
7. Теорема кодирования
27. Теория информации
Метод оптимального кодирования Хафмана6-й
шаг.
Образуем
последовательные
вспомогательные ансамбли путем повторения 4-го
и 5-го шагов, пока в ансамбле не останется
единственное сообщение с вероятностью единица.
7-й шаг. Проводя линии, соединяющие
сообщения,
образующие
последовательные
подмножества, получаем дерево, в котором
отдельные сообщения являются концевыми
узлами. Соответствующие им кодовые слова
можно построить, приписывая различные символы
из заданного алфавита ветвям, исходящим из
каждого промежуточного узла. Только один из
промежуточных узлов может иметь меньше чем D
Лекция 7. Теорема
ветвей, а именно узел, образованный
накодирования
2-м шаге.
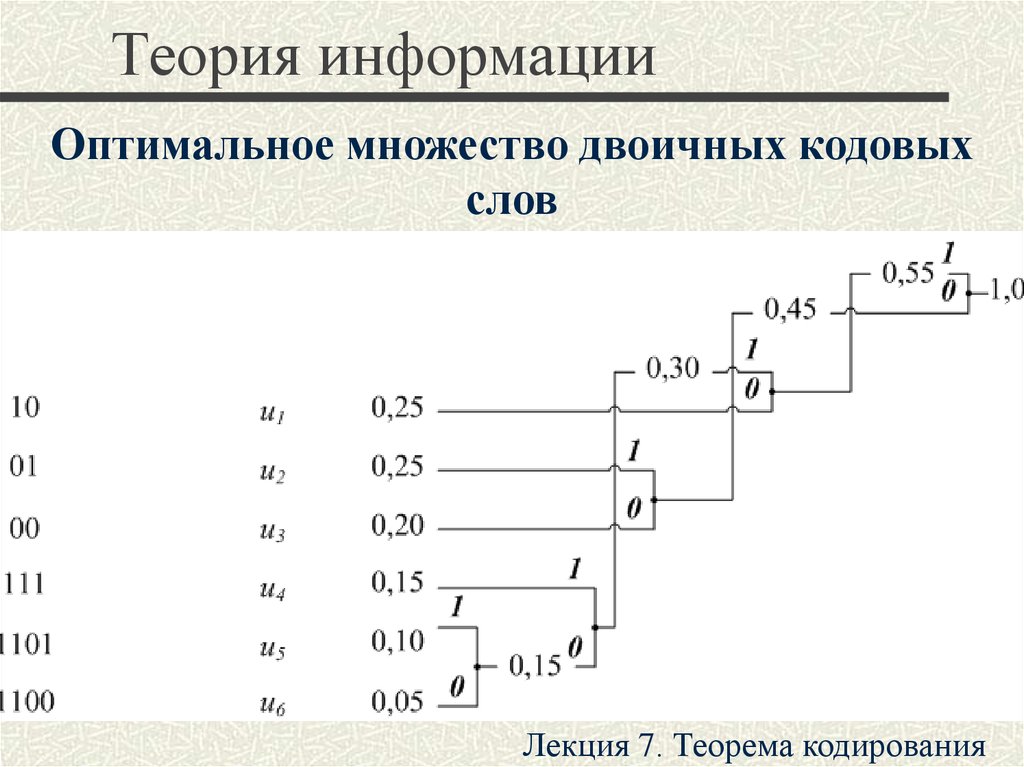
28. Теория информации
Оптимальное множество двоичных кодовыхслов
Лекция 7. Теорема кодирования
29. Теория информации
Оптимальное множество троичных кодовыхслов
Лекция 7. Теорема кодирования
30. Теория информации
Метод оптимального кодирования ХафманаУсловие 1. Сообщениям меньшей вероятности
должны быть сопоставлены слова большей длины.
Условие 2. Два наименее вероятных сообщения
должны соответствовать кодовым словам одной и
той же длины n M (максимальная длина), т. е. узлам
одного и того же порядка.
Условие 3. Число i n M
концевых узлов
порядка n M , сопоставленных сообщениям, и число
i nM 1 – промежуточных узлов порядка nM 1
должны удовлетворять неравенству
D i n M 1 i n M D
1 7. Теорема кодирования
Лекция
31. Теория информации
Метод оптимального кодирования ХафманаУсловие 4. Из каждого промежуточного узла
порядка меньшего, чем n M 1 , должно исходить D
ветвей.
Условие 5. Предположим, что некоторый
промежуточный узел преобразован в концевой, т. е.
исключены все порождаемые им ветви и узлы.
Сопоставим этому узлу составное сообщение,
имеющее вероятность, равную сумме вероятностей
сообщений,
сопоставленных
исключенным
концевым узлам. Тогда, если первоначальное
дерево было оптимальным для исходного ансамбля
сообщений,
новое
дерево
должно
быть
Лекция 7. Теорема
кодирования
оптимальным для нового ансамбля
сообщений.
32. Теория информации
Метод оптимального кодирования ХафманаВспомогательное
условие
6.
Каждый
промежуточный узел порядка, меньшегоnM, должен
порождать D ветвей.
Лекция 7. Теорема кодирования
33. Теория информации
Построение оптимального кода для русскогоалфавита
При кодировании двоичных номеров букв:
n 5; I1c 0,884бит
Лекция 7. Теорема кодирования
34. Теория информации
Построениеоптимального кода
для русского
алфавита
Лекция 7. Теорема кодирования
35. Теория информации
Построение оптимального кода для русскогоалфавита ( n 4,42; I1c 0,994бит )
Лекция 7. Теорема кодирования































 informatics
informatics








