Similar presentations:
Основы теории информации и кодирования
1.
ЛекцияОсновы теории информации и
кодирования
2.
1.1. Понятие информации.Свойства информации.
1.2. Измерение информации
1.3. Представление информации в
компьютере
3.
1.1. Понятие информации.Свойства информации.
4.
Понятие информатикиИнформатика – область человеческой
деятельности, связанная с методами
получения, хранения, обработки,
передачи и представления
информации с помощью
компьютерной техники и средств
связи.
5.
Понятие информацияВ
информатике
понятие
информация рассматривают как
совокупность полезных сведений об
окружающем
мире,
которые
циркулируют в природе и обществе,
их
параметрах,
свойствах,
уменьшающих имеющуюся о них
степень неопределённости.
6.
Свойства информацииРелевантность
̶
способность
информации
соответствовать нуждам потребителя.
Полнота – это исчерпывающая характеристика
отображаемого объекта или процесса.
Своевременность ̶ соответствие нуждам потребителя в
нужный момент времени.
Достоверность ̶ отсутствие скрытых ошибок.
Доступность ̶ возможность получения информации
данным потребителем.
Защищенность – невозможность несанкционированного
использования или изменения информации.
Эргономичность ̶ удобство формы или объёма
информации с точки зрения данного потребителя.
Адекватность
–
однозначное
соответствие
отображаемому объекту или явлению.
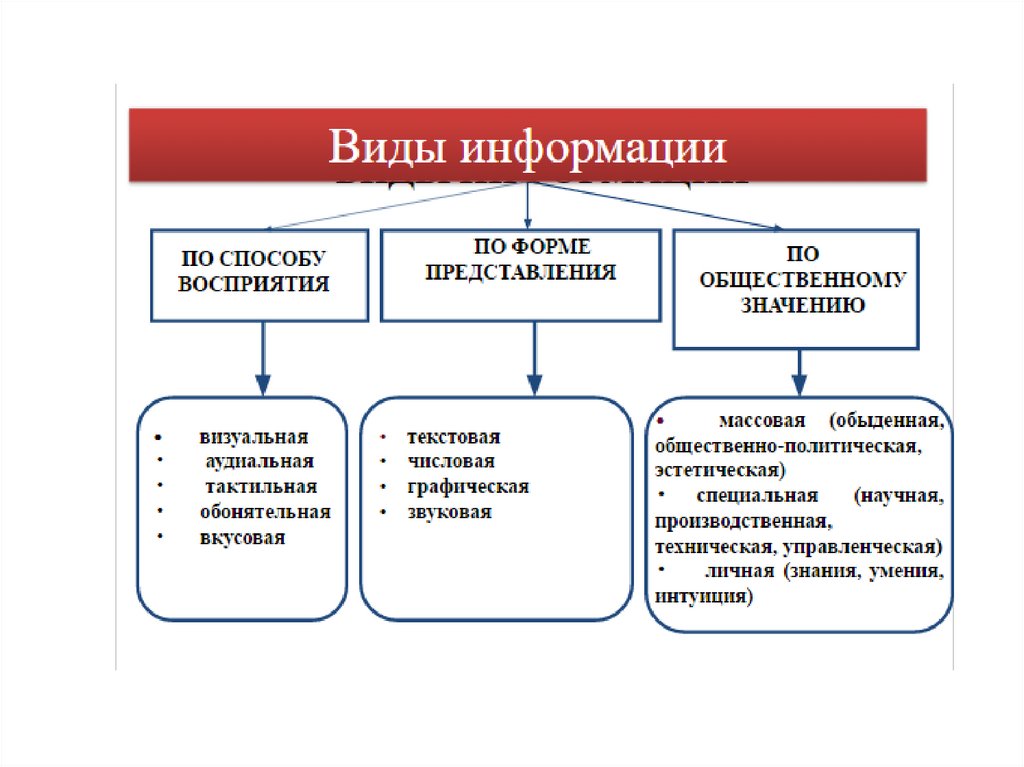
7.
8.
1.2. Измерение информации9.
Единицы измерения информацииВосемь двоичных знаков называют байтом.
Число кодовых комбинаций вычисляется так 28 =
256.
Более крупные единицы измерения информации:
1 Кбайт – 1024 байта - 210 байт;
1 Мбайт – 1024 Кбайта - 220 байт;
1 Гбайт – 1024 Мбайта - 230 байт;
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
10.
Обработка информацииОдной из основных операций, выполняемых над
информацией, является обработка информации.
Обработка информации – получение одних
информационных
объектов
из
других
информационных объектов путем выполнения
некоторых алгоритмов.
Средства обработки информации —
это
всевозможные устройства и системы, созданные
человечеством, и в первую очередь, компьютер —
универсальная
машина
для
обработки
информации.
11.
Меры информацииСтруктурная
Статистическая
Семантическая
12.
Меры информацииВ структурном аспекте рассматривается строение
массивов информации и их измерение простым
подсчетом информационных элементов или
комбинированным методом.
При
статистическом
подходе
используется
понятие энтропии как меры неопределённости,
учитывающей
вероятность
появления,
информированность того или иного сообщения.
Семантический подход позволяет выделить
полезность или ценность информационного
сообщения.
13.
Структурная мераПри
использовании
структурных
мер
информации учитывается только дискретное
строение
сообщения,
количество
содержащихся в нём информационных
элементов, связей между ними.
При структурном подходе различаются меры
информации :
Геометрическая;
Комбинаторная;
Аддитивная.
14.
Структурная мераГеометрическая
мера
предполагает
измерение
параметра
геометрической
модели
информационного
сообщения
(длины, площади, объёма и т.п.) в дискретных
единицах.
Определяет
максимально
возможное
количество информации в заданных объемах,
которая определяется как сумма дискретных
значений по всем измерениям (координатам).
15.
Структурная мераПример:
Пусть сообщение 5555 6666 888888 закодировано одним из
специальных методов эффективного кодирования - кодирование
повторений - и имеет вид: 5(4) 6(4) 8(6).
Требуется измерить информацию в исходном и закодированном
сообщениях геометрической мерой и оценить эффективность
кодирования.
В качестве информационного элемента зададимся символом
сообщения.
Тогда: I(исх) = L(исч) = 14 символов; I(закод) = L(закод) = 12 символов,
где I(исх) , I(закод)- количества информации, соответственно, в исходном
и закодированном сообщениях; L(исч) , L(закод) - длины (объёмы) тех же
сообщений, соответственно.
Эффект кодирования определяется как разница между I(исх) и I(закод) и
составляет 2 символа.
Очевидно, геометрическая мера не учитывает, какими символами
заполнено сообщение.
Так, одинаковыми по количеству информации, измеренной
геометрической
мерой,
являются,
например,
сообщения
«компьютер» и «программа».
16.
Аддитивная мера (мера Хартли)Хартли впервые ввел специальное обозначение для
количества информации - I и предложил следующую
логарифмическую зависимость между количеством
информации и мощностью исходного алфавита:
I = L log2N
где I – количество информации, L – длина сообщения, N –
число возможных выборов (мощность исходного
алфавита).
При исходном алфавите {0,1}; L = 1; h = 2 и основании
логарифма, равном 2, имеем I = 1*log22 = 1.
Данная формула даёт аналитическое определение бита
по Хартли: это количество информации, которое
содержится в двоичной цифре.
Единицей измерения информации в аддитивной мере
является бит.
17.
Статистическая мераСтатистическая
мера
количества
информации
оперирует с обезличенной информацией, не
выражающей смыслового отношения к объекту.
В соответствии с этой мерой рассматривается не само
событие, а информация о нём.
Количество
информации,
с
точки
зрения
статистической меры информации невозможно
определить
без
рассмотрения
понятия
неопределенности (энтропии) состояния системы.
Это связано с тем, что в действительности получение
информации о какой-либо системе всегда связано с
изменением степени неосведомленности получателя о
состоянии этой системы.
18.
Статистическая мераСобытия можно рассматривать как
возможные исходы некоторого опыта,
причем все исходы этого опыта составляю
полную группу событий.
Пусть имеется N возможных исходов опыта,
из них k разных типов, а i-й исход повторяется
ni раз и вносит информацию, количество
которой оценивается как Ii.
Тогда средняя информация, доставляемая
одним опытом:
19.
Статистическая мераНо количество информации в каждом исходе
связано с его вероятностью pi и выражается в
двоичных единицах (битах)
где pi – вероятность того, что система
находится в i – м состоянии.
20.
Статистическая мераПример:
Рассмотрим передачу сообщения по каналу связи, представляющего собой
буквы русского алфавита (32 символа). Вероятность появления в сообщении
символа «а» и символа «я» различна. Обозначим вероятность появления i-го
символа через pi, i=1,2,…32. За количество информации, приходящейся на один
символ i выбирается величина log2(1/pi). Сложив количество информации для
всех 32 символов и, разделив на 32, получим среднее количество информации,
передаваемой одним символом.
21.
Статистическая мераПример:
Какова мощность алфавита, с помощью которого
записано сообщение, содержащее 2048 символов, если
его объем составляет 1,25 Кбайта.
Решение:
Перевести информационный объем сообщения в биты:
I = 1,25 * 1024 * 8 = 10 240 бит.
Определить количество бит, приходящееся на один
символ:
10 240 бит : 2 048 = 5 бит.
По формуле (1) определить количество символов в
алфавите:
N = 2I = 25 = 32.
22.
Статистическая мераПример
1. Вычислить какой объем памяти компьютера
потребуется для хранения одной страницы текста
на английском языке, содержащей 2400 символов.
Решение: Мощность английского алфавита,
включая разделительные знаки, N = 32. Тогда для
хранения такой страницы текста в компьютере
понадобится 2400 · log2 32 бит = 2400 · 5 =12000
бит = 1500 байт
23.
Статистическая мераПример
2. Вычислить какое количество информации будет
содержать зрительное сообщение о цвете
вынутого шарика, если в непрозрачном мешочке
хранятся 10 белых, 20 красных, 30 синих и 40
зеленых шариков.
Решение: Всего шариков 10 + 20 +30 +40 = 100
Вероятности сообщений о цвете следующие: Рб =
10/100 =0,1; Рк = 20/100 =0,2; Рс = 30/100 =0,3; Рз =
40/100 =0,4 События не равновероятны, поэтому
воспользуемся формулой Шеннона: I=- ∑ pi log 2pi =
- (0,1· log2 0,1+ 0,2 · log2 0,2+ 0,3 · log2 0,3+ 0,4 · log2
0,4) =1бит
24.
Статистическая мераМаксимальное значение энтропии достигается при p = 0,5, когда
два состояния равновероятны.
При вероятностях р = 0 или р = 1, что соответствует полной
невозможности или полной достоверности события, энтропия
равна нулю.
Например, пусть опыт состоит в сдаче студентом экзамена по
информатике. Очевидно, у этого опыта всего 4 исхода (по
количеству возможных оценок, которые студент может получить
на экзамене). Тогда эти исходы составляют полную группу
событий, т.е. сумма их вероятностей равна 1.
Если студент учился хорошо в течение семестра, значения
вероятностей всех исходов могут быть такими: р(5) = 0.5; р(4) =
0.3; p(3) = 0,1; р(2) = 0.1, где запись p(j) означает вероятность
исхода, когда получена оценка j (j = {2, 3, 4, 5}).
Если студент учился плохо, можно заранее оценить возможные
исходы сдачи экзамена, т.е. задать вероятности исходов,
например, следующим образом: p(5) = 0.1; p(4) = 0.2; р(3) = 0.4;
р(2) = 0.3.
25.
Статистическая мераПример 2.
Определить количество информации, содержащейся в
сообщении о результате сдачи экзамена для студентахорошиста.
Пусть I(j) - количество информации в сообщении о получении
оценки j. В соответствии с формулой Шеннона имеем:
I(5) = -log2 0,5 = 1, I(4) = -Iog2 0,3 = 1,74, I(3) = -log2 0,1 = 3,32, I(2)
= -log2 0,1 = 3,32.
Пример 3
Определить количество информации, содержащейся в
сообщении о результате сдачи экзамена для нерадивого
студента:
I(5) = -Iog20,1 = 3,32, I(4) = -log2 0,2 = 2,32, I(3) = -Iog2 0,4 = 1,32,
I(2) = -Iog2 0,3 = 1,74.
Таким образом, количество получаемой с сообщением
информации тем больше, чем неожиданнее данное сообщение.
26.
Семантическая мераСреди семантических мер наиболее
распространены:
содержательность,
логическое количество,
целесообразность,
существенность,
полезность (учитывают прагматику информации)
истинность (учитывают семантику информации) .
Применяется при оценке эффективности получаемой
информации и ее соответствия реальности.
27.
1.3. Представление информации вкомпьютере
28.
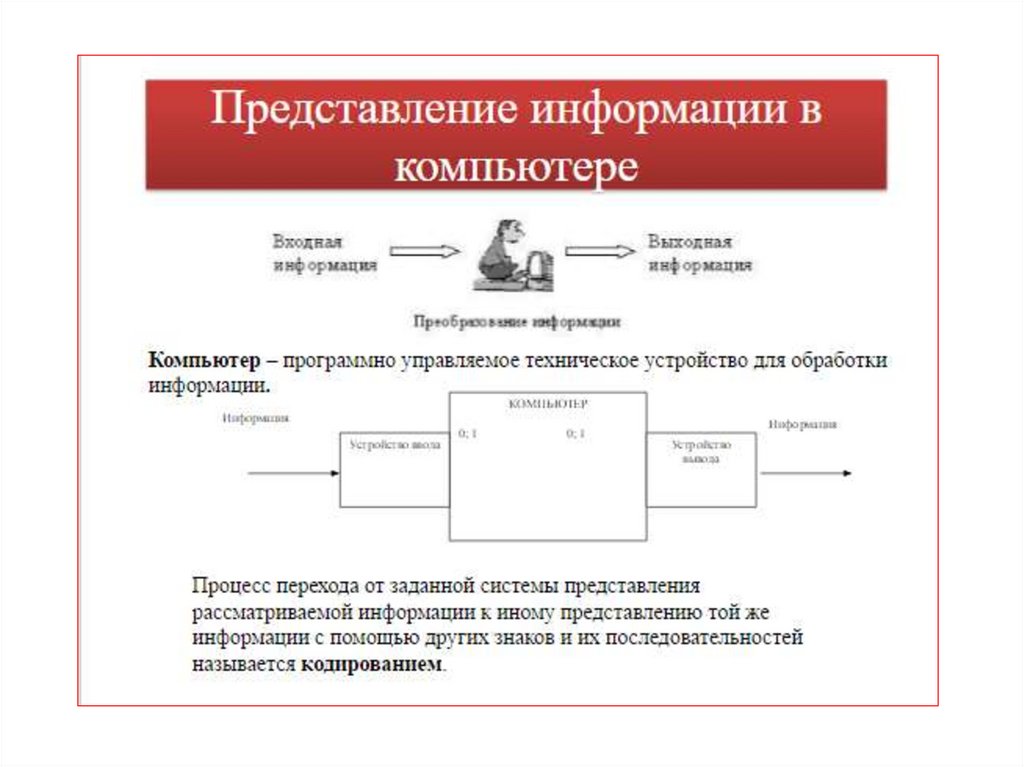
Представление информации вкомпьютере
Любая ЭВМ предназначена для обработки,
преобразования и хранения данных.
Для выполнения этих функций ЭВМ должна
обладать некоторым способом представления
этих данных.
Представление данных заключается в их
преобразовании в вид, удобный для
последующей обработки либо пользователем,
либо ЭВМ.
29.
30.
Кодирование информацииКомпьютер является универсальным
преобразователем дискретной информации,
обеспечивающий также её передачу, хранение и
воспроизведение.
Для автоматизации работы с данными
(зарегистрированные сигналы) различного типа,
очень важно унифицировать их форму
представления – для этого обычно используется
приём кодирования, т.е. выражение данных
одного типа через данные другого типа.
Кодирование – это процесс представления
информации в виде кода.
А код, в свою очередь – это набор условных
обозначений для представления информации.
31.
Кодирование текстовой информацииВ качестве международного стандарта
принята кодовая таблица ASCII.
В системе ASCII закреплены две таблицы
кодирования – базовая и расширенная.
Базовая таблица значения кодов от 0 до 127,
а расширенная от 128 до 255.
Первые 32 кода базовой таблицы, начиная с
нулевого, отданы производителям
аппаратных средств. В этой области находятся
управляющие коды.
32.
Кодирование текстовой информацииС 32 кода по 127 размещены коды символов
английского алфавита, знаков препинания,
цифр, арифметических действий и некоторых
вспомогательных символов.
С 128 по 255 используется для национальных
алфавитов и символов для рисования линий
(псевдографики). В разных странах могут
использоваться различные варианты второй
кодовой таблицы.
В настоящее время существуют пять
различных кодировок кириллицы ( КОИ8-Р,
Windows, которая сокращенно обозначается
СР1251, MS-DOS, Macintosh и ISO)
33.
Кодирование текстовой информацииВ этих кодировках для кодирования одного символа
используется 8 бит.
8-разрядный код позволяет закодировать 256 различных
символов.
Система кодирования, основанная на 16-разрядном
кодировании символов получила название универсальной
– UNICODE.
Шестнадцать разрядов позволяют обеспечить уникальные
коды для 65 536 различных символов – этого достаточно
для размещения в одной таблице символов большинства
языков планеты, а также множество математических,
музыкальных, химических и прочих символов.
34.
Кодирование графических данныхГрафические объекты в компьютере можно
создавать и хранить двумя способами: как
растровое или векторное.
Качество растрового изображения
определяется его разрешением
(количество точек по вертикали и по
горизонтали) и используемой палитрой
цветов.
35.
Кодирование графических данныхЛинейные координаты и индивидуальные свойства каждой
точки (яркость) можно выразить с помощью целых чисел.
Для кодирования яркости любой черно-белой точки
достаточно восьмиразрядного двоичного числа.
Черно-белые точки представляют 256 градациями серого
цвета. Такой метод называется индексным.
Для кодирования цветных графических изображений
используется принцип декомпозиции, который заключается
в разложении произвольного цвета на основные
составляющие.
При этом используются составляющих три основных цвета:
красный (Read, R), зелёный (Green,G), синий (Blue,B). Эта
система кодирования называется RGB.
На кодирование цветных точек необходимо 24 разряда. При
этом можно получить 16,5 млн. различных цветов.
36.
Кодирование графических данныхВекторное изображение представляет собой
графический объект, состоящий из элементарных
отрезков и дуг.
Положение этих элементарных объектов
определяется координатами точек и длиной
радиуса.
Для каждой линии указывается ее тип (сплошная,
пунктирная, штрих-пунктирная), толщина, и цвет.
Информация о векторном изображении
кодируется как обычная буквенно-цифровая и
обрабатывается специальными программами.
37.
Кодирование звуковой информацииВ аналоговой форме звук представляет собой
волну с непрерывно меняющейся амплитудой
и частотой.
При преобразовании звука в цифровую
дискретную форму производится временная
дискретизация, при которой в определенные
моменты времени амплитуда звуковой волны
измеряется и квантуется, т.е. ей присваивается
определенное значение из некоторого
фиксированного набора.
Данный метод называется еще импульснокодовой модуляцией РСМ.
38.
Кодирование звуковой информацииМетод FM (FrequencyModulation) он
основан на том, что теоретически любой
сложный звук можно разложить на
последовательность простейших
гармонических сигналов разных частот,
каждый из которых представляет
правильную синусоиду и поэтому может
быть описан кодом.
39.
Кодирование звуковой информацииМетод таблично-волнового синтеза (WaveTable) использует образцы звуков (сэмплов),
хранящихся в специальных таблицах.
При этом числовой код отражает тип
инструмента, номер его модели, высоту тона,
продолжительность и интенсивность звука,
динамику его изменения, некоторые
параметры среды, в которой происходит
звучание и другие параметры,
характеризующие особенности звука.
Этот метод даёт более качественное звучание,
т.к. в качестве образцов использует реальные
звуки.
40.
Системы счисленияСистемы счисления – это совокупность
правил наименования и изображения
чисел с помощью набора символов,
называемых цифрами.
В любой системе счисления выбираются
некоторые базисные числа, все остальные
числа получаются в результате операций
над базисными числами. Системы
счисления делятся на позиционные и
непозиционные.
41.
Системы счисленияПозиционные системы счисления:
двоичная, десятичная, восьмеричная,
шестнадцатеричная.
Система счисления, применяемая в
современной математике,
является позиционной десятичной
системой. Ее основание равно десяти, т.к.
запись любых чисел производится с
помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7,
8, 9.
42.
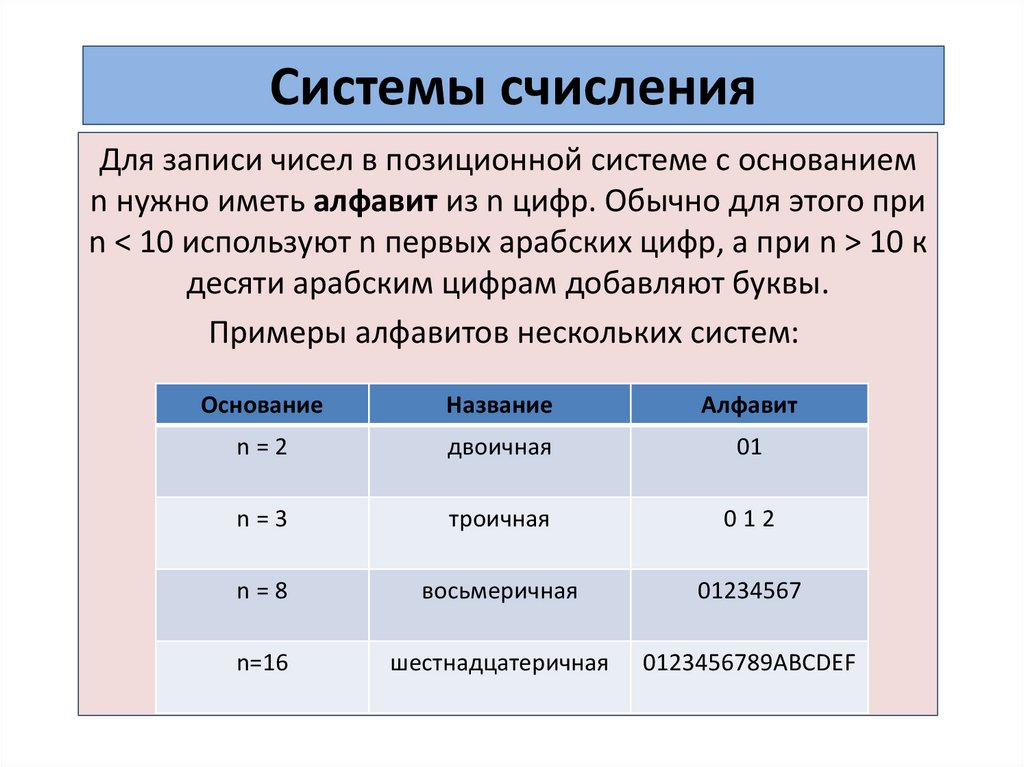
Системы счисленияДля записи чисел в позиционной системе с основанием
n нужно иметь алфавит из n цифр. Обычно для этого при
n < 10 используют n первых арабских цифр, а при n > 10 к
десяти арабским цифрам добавляют буквы.
Примеры алфавитов нескольких систем:
Основание
Название
Алфавит
n=2
двоичная
01
n=3
троичная
012
n=8
восьмеричная
01234567
n=16
шестнадцатеричная
0123456789ABCDEF
43.
Системы счисленияВ непозиционных системах счисления от положения
цифры в записи числа не зависит величина, которую она
обозначает. Примером непозиционной системы
счисления является римская система (римские цифры).
В римской системе в качестве цифр используются
латинские буквы:
I
V
X
L
C
D
M
1
5
10
50
100
500
1000
44.
Системы счисленияЗапись произвольного числа Х в К-ичной
позиционной системе счисления
основывается на представлении этого
числа в виде полинома:
где каждый коэффициент ai может быть
одним из базисных чисел и изображается
одной цифрой.
45.
Системы счисленияВ непозиционных системах счисления
несколько чисел приняты за основные
(например, I, V, X), а остальные получаются
из основных путём сложения (VI, VII) или
вычитания (IV, IX). Такие системы счисления,
в которых любое число получается путём
сложения или вычитания базисных чисел,
называются аддитивными.
Позиционные системы счисления являются
аддитивно-мультипликативным, поскольку
значение числа определяется операциями
умножения и сложения.







































 informatics
informatics








