Similar presentations:
Количественная оценка информации. Единицы количества информации. Лекция № 2
1.
3ПРЕДЛОЖЕНИЯ
КОМПЛЕКС
АНПА“САРМА”
Лекция № 2
«КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ.
ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ»
2.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
2
Определение
Под информацией понимают совокупность сведений о явлениях,
процессах, событиях, фактах и т.д., которые принимает человек в
процессе жизнедеятельности.
Сообщение, получаемое на приемной
стороне, несет полезную информацию
лишь в том случае, если имеется
неопределенность относительно
состояния источника.
Информацию несут в себе те сообщения, которые
снимают неопределенность, существующую до их
поступления.
3.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
3
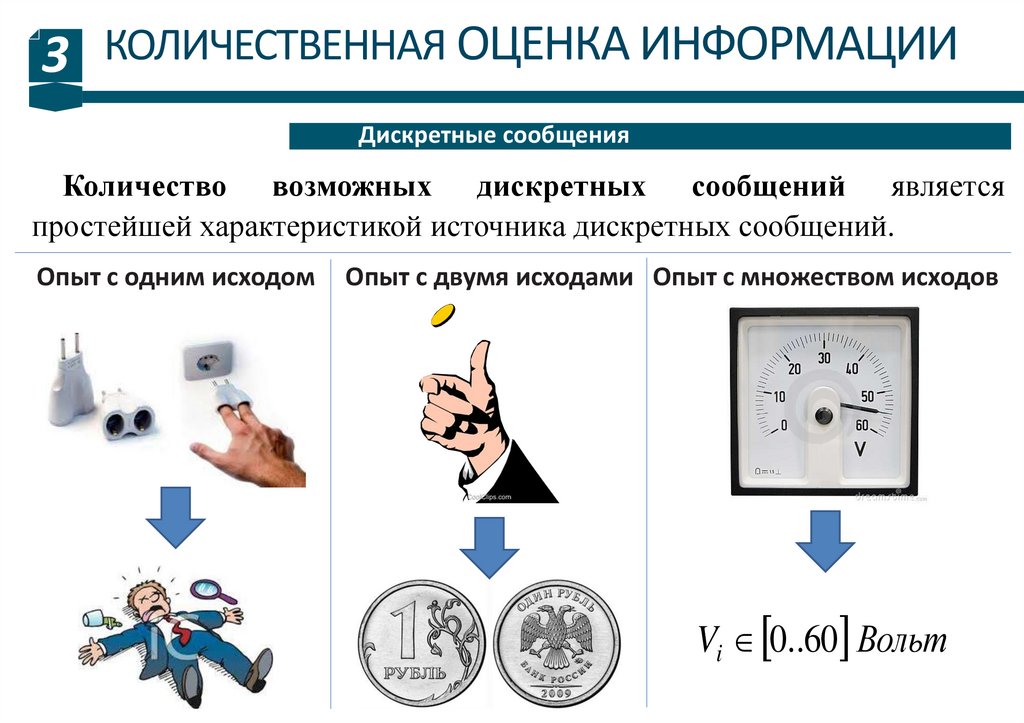
Дискретные сообщения
Количество возможных дискретных сообщений является
простейшей характеристикой источника дискретных сообщений.
Опыт с одним исходом
Опыт с двумя исходами Опыт с множеством исходов
Vi 0..60 Вольт
4.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
4
Общий случай:
m
n
Количество символов сообщения
Количество символов в каждом сообщении
N m
n
(2.1)
Количество различных сообщений длиной n из символом m
Ансамбль А ai , i 1, m
a2
... am
a1
A
p a1 p a2 ... p am
m
p ai 1
i 1
(2.2)
5.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
5
Мера Хартли
В 1928 г. Р. Хартли предложил использовать
логарифмическую функцию от N в качестве
количественной меры информации.
I log N n log m
(2.3)
Единицы измерения – бит.
Для равновероятных символов можно записать
Ральф Винтон Лайон Хартли
30 ноября 1888,
Спрус, Невада — 1
мая 1970, Нью-Джерси) —
американский учёныйэлектронщик
(2.3) (2.4)
1
p a1
m
1
I1 log
log p a1 log 2 N
p a1
(2.4)
(2.5)
(2.5) – Количество информации на символ алфавита
6.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
6
Мера Шеннона
Мера Хартли не отражает вероятностный характер
сообщений. Эту задачу решил в 1946 г. К. Шеннон.
Клод Э́лвуд Ше́ннон
30 апреля 1916 Мичиган,
США — 24 февраля 2001,
Медфорд, Массачусетс,
США) — американский
инженер и математик
a a
1
p ai
Сложное событие:
i j
p ai p a j
Вероятность события:
Количество информации в сложном сообщении:
1
p ai p a j
Такая мера не
обладает свойством
аддитивности
7.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
7
Мера Хартли
Удобнее воспользоваться логарифмической мерой количества информации
1
I ai log
log p ai [бит]
p ai
(2.6)
Количество информации в сложном сообщении:
1
1
1
I ai , a j log
log
log
I ai I a j
p ai p a j
p ai
p a j
Количество информации для единичного исхода:
1
I a1 log 0
1
Прикладная теория цифровых автоматов / К. Г. Самофалов, А. М. Ромлинкевич, В. Н. Валуйский, Ю. С. Каневский, М. М. Пиневич.— К.: Вища шк. Головное изд-во, 1987. — 375 с.
8.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
8
Частная энтропия
1
H ai log
log p ai [бит/символ]
p ai
(2.7)
Количество информации и неопределенность для всей совокупности случайных
сообщений можно получить усреднением по всем событиям
n
n
1
I A p ai log
p ai log p ai
p ai
i 1
i 1
n
H A p ai log p ai
i 1
(2.8)
(2.9)
(2.9) – формула Шеннона для энтропии источника дискретных сообщений
Энтропия это среднестатистическая мера неопределенности знаний
получателя информации относительно состояния наблюдаемого объекта
(источник сообщений)
Кузьмин И.В., Кедрус В.А. Основы теории информации и кодирования с. 115
9.
КОЛИЧЕСТВЕННАЯОЦЕНКА
ИНФОРМАЦИИ
9
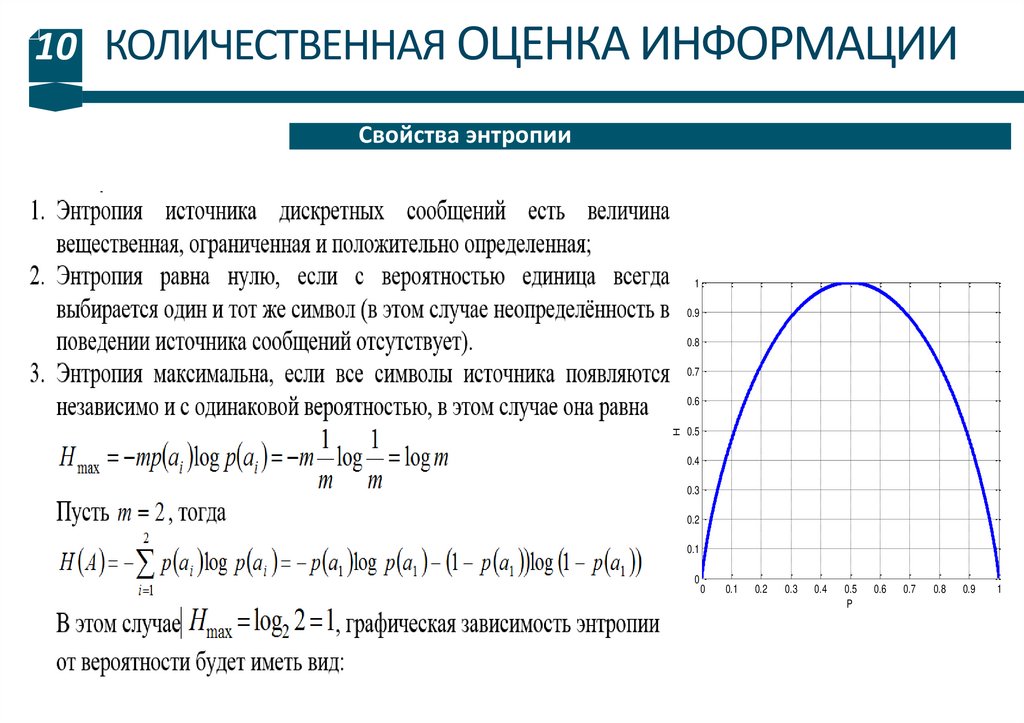
Свойства энтропии:
Чем выше энтропия источника, тем большее количество информации в
среднем закладывается в каждое сообщение, тем сложнее запомнить,
передать или сохранить такое сообщение по каналу связи.
Смысл энтропии Шеннона:
Энтропия дискретной случайной величины это минимум
среднего количества бит, которое нужно передавать по каналу
связи о текущем значении данной случайной величины.
10.
10 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИСвойства энтропии
1
0.9
0.8
0.7
H
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.1
0.2
0.3
0.4
0.5
P
0.6
0.7
0.8
0.9
1
11.
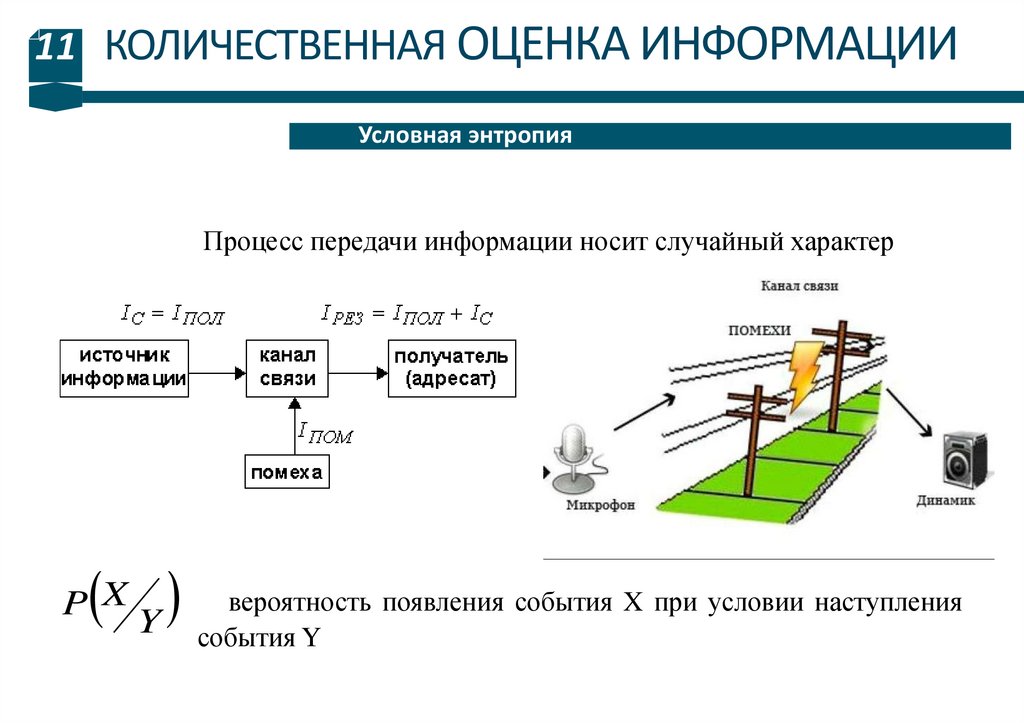
11 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИУсловная энтропия
Процесс передачи информации носит случайный характер
вероятность появления события X при условии наступления
Y события
Y
P X
12.
12 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИУсловная энтропия
P AB
k
n
B
P B l
l
n
k
P AB
k
n
B
P
A P A m
m
n
k
PA
(2.10)
Из (2.10)
A
B
P AB P
P B P
P A
B
A
(2.11)
13.
13 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИЧастная условная энтропия
Различают понятия частной и общей условной энтропии
bj
bj
bj
H
P
log P
a
a
a
i
i
i
j 1
n
Из (2.9)
ai
ai
ai
H
P
log P
b
b
b
j
j
j
i 1
n
(2.12)
14.
14 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИОбщая условная энтропия
Общая условная энтропия сообщения B относительно сообщения А
характеризует количество информации, содержащейся в любом символе
алфавита, и определяется усреднением по всем символам, т.е. по всем состоянием
с учетом вероятности появления каждого из состояний, и равна сумме
вероятностей появления символов алфавита на неопределенность, которая
остается после того как адресат принял сигнал.
n
b
j
B
H
P ai H
A
a
i
i 1
i 1
n
bj
bj
P ai P ai log P ai
j 1
n
bj
bj
P ai P
log P
a
a
i
i
i 1
j 1
n
n
(2.13)
(2.13) общее выражение для определения количества информации на один
символ сообщения для случая неравновероятных символов
15.
15 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИОбщая условная энтропия
со стороны источника
bj
bj
P ai P
log P
A
a
a
i
i
i 1
j 1
H B
со стороны приемника
n
H A
Так как
n
ai
ai
P b j P
log P
B
b
b
j
j
j 1
i 1
n
n
bj
ai
P ai , b j P ai P
P b j P
ai
bj
b
j
B
H
P ai , b j log P
A
a
i
i 1 j 1
H A
n
то из (2.13)
n
ai
P ai , b j log P
B
b
j
i 1 j 1
n
(2.13’)
n
(2.14)
16.
16 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКаналы связи с шумами
Для идеальных условий
I kH
Для равновероятных независимых сообщений
H 1 log 2 N n log 2 m
Для неравновероятных независимых сообщений
m
H 2 A p ai log p ai
i 1
Со стороны источника
Со стороны приемника
n n
b
j
a
B
i
A
H3
P ai , b j log P
H
P
b
,
a
log
P
4
j
i
A
a
B
b
i
j
i 1 j 1
i 1 j 1
n
n
H 5 A, B H 5 B, A P ai , b j log P ai , b j
n
n
i 1 j 1
17.
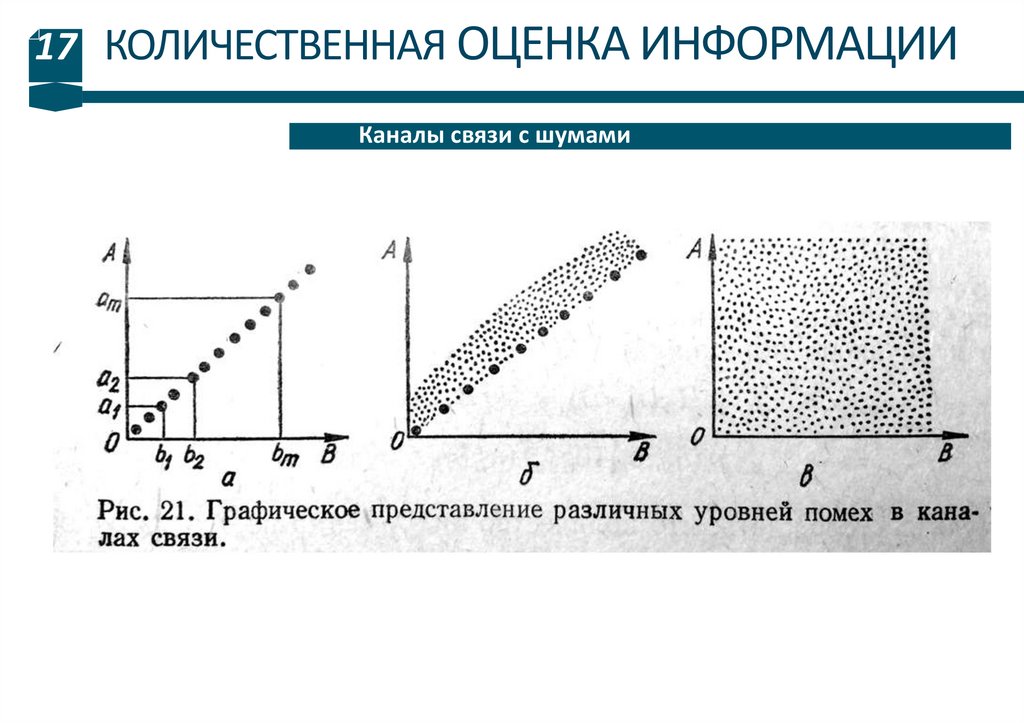
17 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКаналы связи с шумами
18.
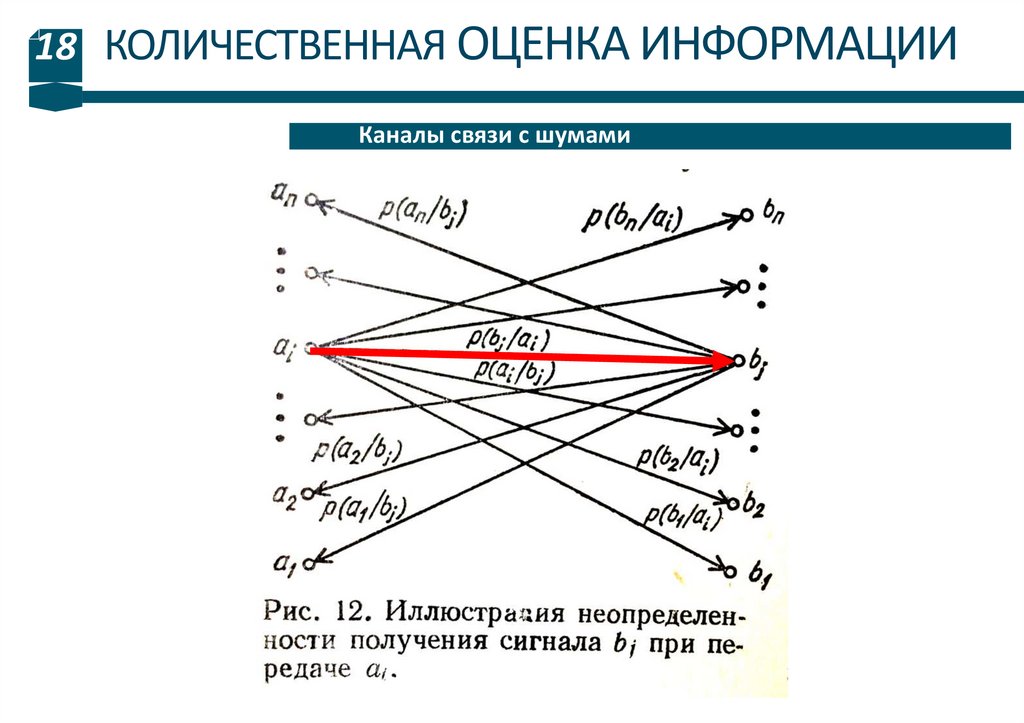
18 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКаналы связи с шумами
19.
19 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКанальная матрица
Канальная матрица матрица, статистически описывающая канал связи.
20.
20 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКанальная матрица (со стороны источника)
Канальная матрица матрица, статистически описывающая канал связи.
p b1 a1 p b2 a1 ... p b j a1 ... p bn a1 1
(2.15)
21.
21 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКанальная матрица (со стороны источника)
b
b
j
j
B
H
P
log P
a
a
a1
1
1
j 1
n
(2.16)
Общая условная энтропия
b
b
1
j
j
B
H
P
log P
A
a
i
n j 1 i 1 ai
(2.17)
(2.18)
n
n
b
b
j
j
H B P ai P
log P
A
a
a
i
i
j 1 i 1
n
n
22.
22 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКанальная матрица (со стороны приемника)
p a1 b j p a2 b j ... p ai b j ... p an b j 1
A
ai
ai
H
log P
b
b
b
j
j
j
i 1
n
Частная условная энтропия
Общая условная энтропия H A
ai
ai
P b j P
log P
B
b
b
j
j
j 1 i 1
n
n
(2.19)
(2.20)
(2.21)
23.
23 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИКанальная матрица
Безусловные вероятности приемника
Энтропия приемника
p b j p ai p b j ai
(2.22)
H B p b j log p b j
(2.23)
n
i 1
n
j 1
Безусловные вероятности источника
p ai p b j p ai b j
(2.24)
H A p ai log p ai
(2.25)
n
Энтропия источника
j 1
n
i 1
24.
24 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИЭнтропия объединения
Энтропия объединения используется для вычисления энтропии совместного
появления статистически зависимых сообщений либо энтропии взаимосвязанных
систем.
бит
H A, B H B, A P ai , b j log P ai , b j
два символа
i 1 j 1
n
n
A H B H A B
Связь с условной энтропией
H A, B H A H B
p a1 , b1
p ai , b j
p a1 , b2
p a1 , bn
(2.26)
(2.27)
p ai , b j p b j
p a2 , b1 p a2 , b2 p a2 , bn i 1
(2.28)
p an , b1 p an , b2 p an , bn
n
p ai , b j p ai
n
j 1
25.
25 КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИЭнтропия объединения
H A p ai log p ai p ai , b j log p ai , b j
n
n
i 1
n
n
n
i 1 j 1
n n
j 1
n
j 1 i 1
i 1
H B p b j log p b j p ai , b j log p ai , b j
j 1
p ai , b j
ai p ai , b j
p
n
p b j
bj
p ai , b j
i 1
p ai , b j
b j p ai , b j
p
n
a
i
p ai
p ai , b j
j 1
(2.29)
I A, B H A H B H B, A
(2.30) I A, B H A H A B
I A, B H B H B A (2.31)




















 informatics
informatics








