Similar presentations:
Прикладная теория информации. Энтропия перерывного источника информации (дифференциальная энтропия)
1. Дисциплина «Прикладная теория информации»
Тема лекции«Энтропия перерывного источника
информации
(дифференциальная энтропия)»
Лектор
Золотов А.Д.,
доцент кафедры «Автоматика ИТ и градостроительство», к.т.н.
2.
На практике встречаются в основном непрерывные источникиинформации. Оценка неопределенности выбора для
непрерывного источника информации имеет определенную
специфику:
Значения реализуемые источником, математически
отображаются непрерывной случайной величиной.
Вероятности значений случайной величины р=0 и не могут
использоваться для оценки неопределенности (информации)
Поэтому неопределенность выбора значения непрерывной
случайной величины необходимо связать с плотностью
распределение вероятностей их значений.
3.
Разобьем диапазон изменений непрерывной случайной величины U,характеризуется плотностью распределения вероятностей p(u) на конечное
число и интервалов, шириной ∆u.
При реализации особого значения и принадлежащего интервалу ( ), будем
считать, что реализованная значение дискретной случайной величины U.
Вероятность реализаций значения и из этого интервала:
u j u
p(u j u u j u )
p(u)du p(u ) u
j
u
4.
Тогда энтропия дискретной случайной величины Un
H (u ) p(u j ) u log p(u j ) u
(21)
j 1
Или
H (u ) p(u j ) u log p(u j ) p(u j ) u log u (23)
Так как
p(u) u 1
То
H (u ) p(u j ) u log p(u j ) log u
.
(24)
5.
u 0Переходя к пределу
lim H (u ) H (u ) p (u ) log p (u )du lim log u
(25)
Первый член в правой части соотношения (25) имеет
конечное значение которое зависит только от значения
распределения непрерывного случайной величины U и не
зависит от шага квантования имеет такую же структуру как и
энтропия дискретного источника.
Второй член зависит только от шага квантования
В качестве меры неопределенности непрерывного источника
принимают первый член соотношении (25)
h(u ) p (u ) log p (u )du
(26)
Которая называется дифференциальной энтропией, т.к.
использовалось
только дифференциального значения
.
распределения.
Ее можно трактовать, как среднего неопределенность выбора
случайной величины U с произвольным законом распределения.
6.
Аналогично найдем выражение для условной энтропии непрерывного источникаинформации.
p(u, z )
H (u / z ) p(u, z ) log
dudz lim log u
p
(
z
)
u 0
p(u, z )
H (u / z ) p(u, z ) log
dudz
p( z )
(27)
(28)
Она характеризует неопределенность выбора непрерывной случайной величины U при
условии, что известны результаты реализации значений другой, статически связанной с
ней непрерывной случайной величины Z.
7.
Свойства дифференциальной энтропии1. Дифференциальная энтропия является относительной мерой
неопределенности. Ее значение зависит от масштаба
случайной величины U, а следовательно и от выбора единицы
ее измерения. Если изменить масштаб случайной величины в
K раз, оставив неизменный масштаб равномерно
распределенной в единичном интервале случайной величины
h(u ) h(u ) log K
2. Дифференциальная энтропия не зависит от конкретных
значении случайной величины U, и в частности, от изменения всех
ее значений на постоянное. Масштаб U при этом не меняется:
h(u ) h(u )
8.
3. Если единственным ограничением для случайной величины Uявляется область ее возможных значении , , то
дифференциальной энтропией обладает равномерное
распределение вероятностей в этой области:
(29)
h(u ) log( a)
4. Если ограничение на U отсутствует, но известно что
дисперсия ее ограничена, то максимальной энтропией обладает
нормальное распределение величины U.
(30)
h max( u ) log 2 2 *e
Соотношения для дифференциальной энтропии объединения
статически зависимых непрерывных источников аналогичны
соотношении в формулам для дискретных источников.
h(u / z ) h(u ) h(u / z ) h( z ) h( z / u )
(31)



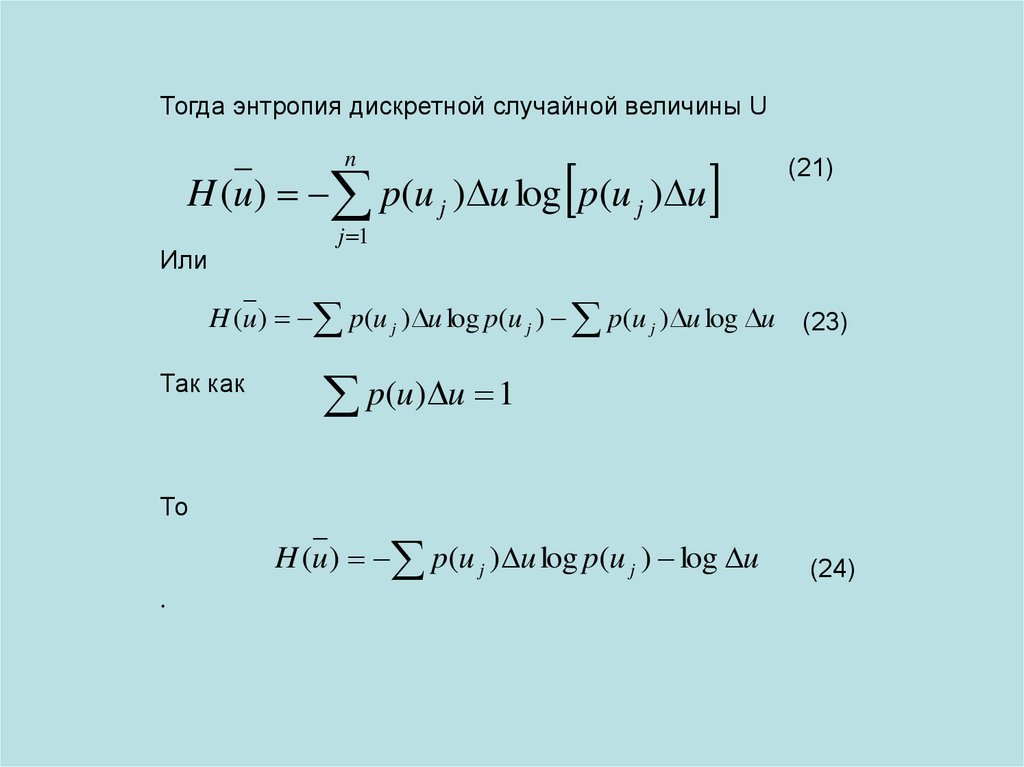




 informatics
informatics








