Similar presentations:
Приращение функции. Понятие производной
1.
Тема урока:Приращение функции.
Понятие производной
2.
Основоположники дифференциального иинтегрального исчисления
Исаак Ньютон (1642-1727)-
английский физик, математик
и астроном
Готфрид Вильгельм Лейбниц
(1646-1716) – немецкий
философ , математик, физик
3.
СВЕДЕНИЯ ИЗ ИСТОРИИВ конце семнадцатого века великий
английский ученый Исаак Ньютон открыл
общий способ описания связи между
путем и скоростью движения.
Основными математическими
понятиями, выражающими эту связь,
являются производная и скорость. Честь
открытия основных законов
математического анализа также
принадлежит великому математику
Готфриду Вильгельму Лейбницу.
4.
Цитата Г.В. Лейбница«Общее искусство знаков представляет
чудесное пособие, так оно разгружает
воображение… Следует заботиться о
том, чтобы обозначения были удобны
для открытий. Обозначения коротко
выражают и отображают сущность
вещей. Тогда поразительным образом
сокращается работа мысли.»
5.
Теория без практики мертва или бесплодна,практика без теории невозможна или пагубна.
Для теории нужны знания,
для практики, сверх всего того, и умение
(А.Н. Крылов)
Алексей Николаевич Крылов- русский и советский математик,
механик и кораблестроитель
6.
Пусть дана функция у=f(х)y
x
f ( x) f ( x0 x)
f
f ( x0 )
0
х0
x
х
x
∆х=хх0 –х –приращение
аргумента
Пусть
произвольная точка
в окрестности
Разность f(x)-f(x0) называется приращением функции
фиксированной точки х0
и обозначается f
Разность х-х0 называется
аргумента и обозначается
∆f = f(x)-f(x0) приращением
или
∆0)x -=x-x
0
х=х
0+ ∆ x
∆f =f(x0+ ∆x)-f(x
приращение
функции
7.
Пример 1:Найти приращение аргумента и приращение
2
функции в точке х0, если
f ( x) x
x 1,9
x0 2
Решение:
x x x0 ;
x 1,9 2 0,1;
f f ( x) f ( x0 );
f f (1,9) f (2) 1,9 2 3,61 4 0,39
2
2
Ответ : x 0,1; f 0, 39
8.
Геометрический смысл приращенияy
функции
y=kх+b
В
f ( x) f ( x0 x)
f
f ( x0 )
0
А
х0
f
С
x
x
х
k tg
k tg
f
x
ABC - прямоугольный
x
BC
tg
AC
Прямая l , проходящая через
любые две точки графика функции,
-угловой коэффициент
называется секущей к графику
секущей к графику
функции.
функции
9.
№184(а )1 2
f ( x) x ; x0 0; x 1
2
Решение :
tg
x x x0 ;
f f ( x) f ( x0 );
x 1 0 1;
1
k tg
2
f
;
x
1 2 1 2 1
f f (1) f (0) 1 0
2
2
2
0 острый
1
Ответ : tg ; острый
2
10.
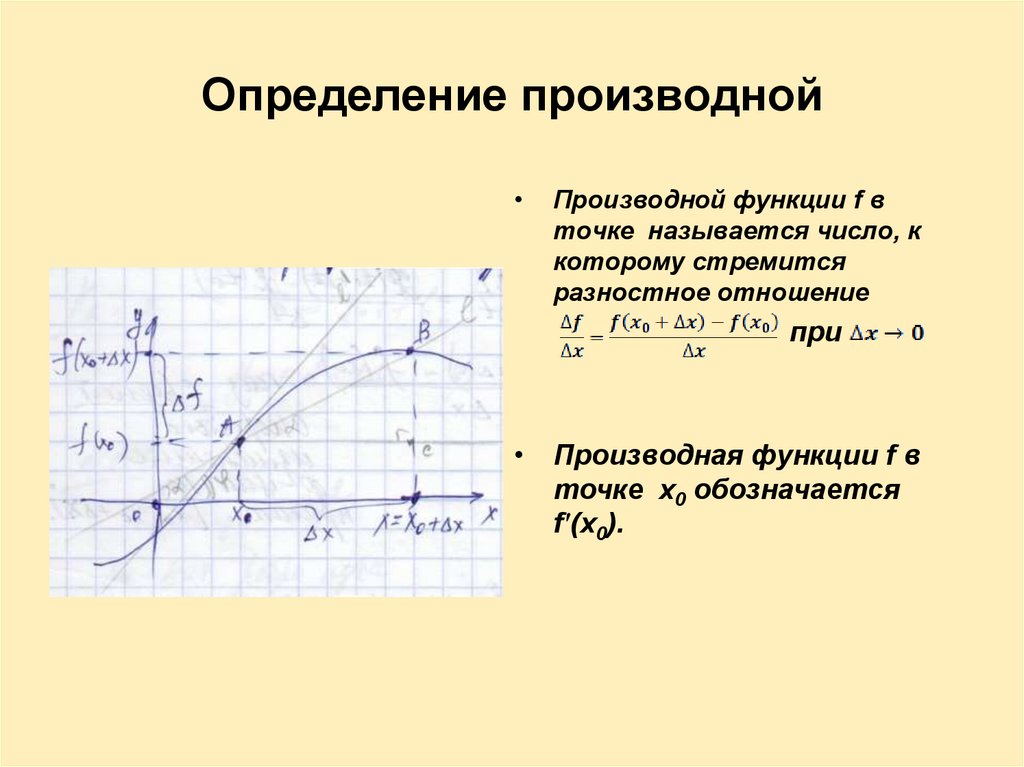
Определение производнойПроизводной функции f в
точке называется число, к
которому стремится
разностное отношение
при
• Производная функции f в
точке х0 обозначается
f'(x0).
11.
Найти производные следующих функций, используяопределение производной.
1) f(x) = x2;
2) f(x) = x3;
3) f(x) = kx+b;
4) f(x) = c.
12.
Самостоятельная работаВариант 1
• № 178 (в)
• № 181 (в)
• № 192 (а)
• № 193 (в)
Вариант 2
• № 178 (г)
• № 181 (г)
• № 192 (в)
• № 193 (г)
13.
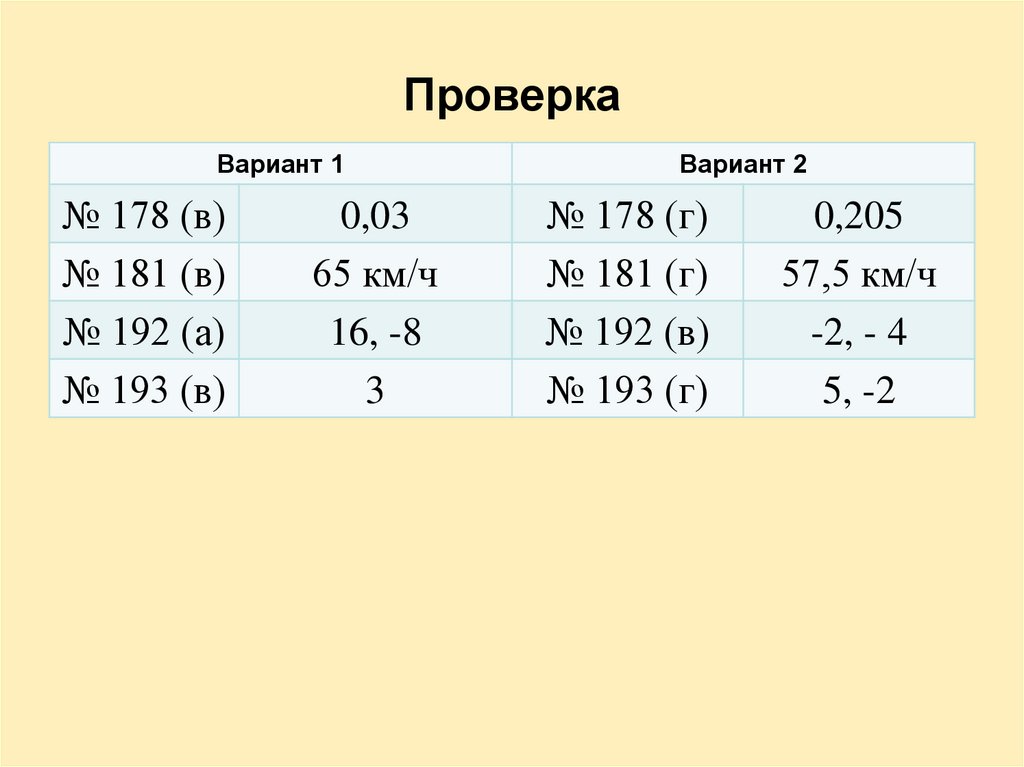
ПроверкаВариант 1
№ 178 (в)
№ 181 (в)
№ 192 (а)
№ 193 (в)
0,03
65 км/ч
16, -8
3
Вариант 2
№ 178 (г)
№ 181 (г)
№ 192 (в)
№ 193 (г)
0,205
57,5 км/ч
-2, - 4
5, -2
14.
Домашнее задание№ 179 (а, в)
№ 187 (в)
№ 196 (б)












 mathematics
mathematics