Приращение функции

1. Приращение функции

Преподаватель: Галынина И.А.

2. Цели урока:

• сформировать понятия приращения
функции, секущей, геометрического и
физического смысла приращения
функции;
• развивать навыки исследования
функции, вычислительные навыки;
• воспитывать трудолюбие,
аккуратность, точность в расчетах.

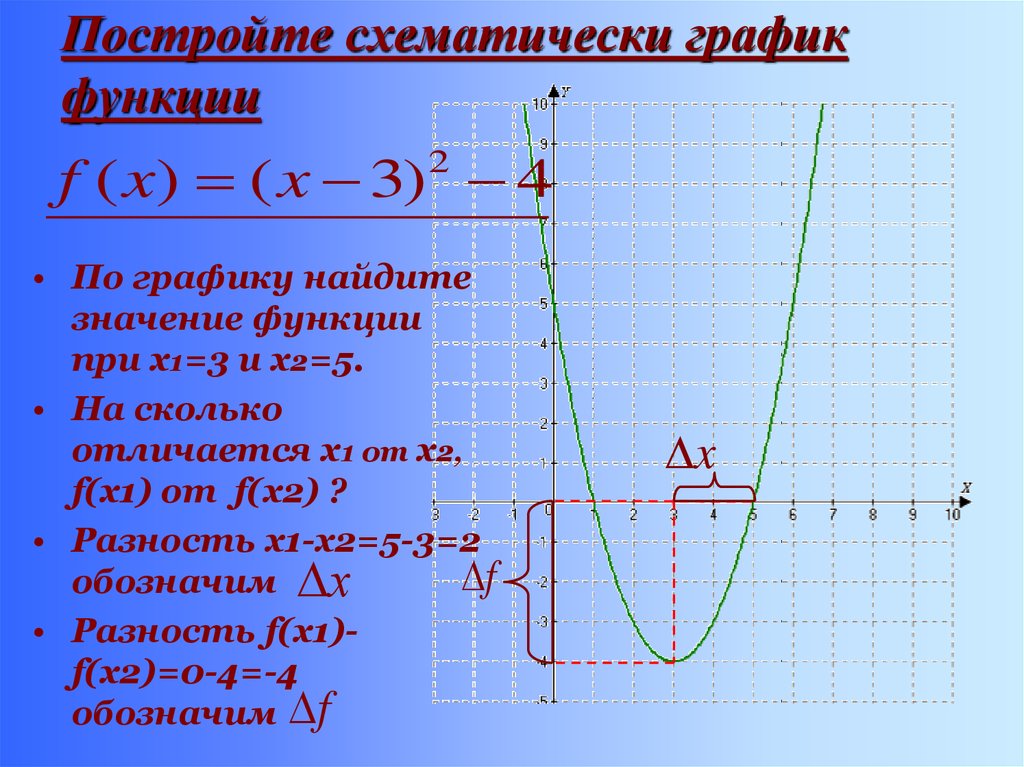
3. Постройте схематически график функции

f ( x) ( x 3) 4
2
• По графику найдите
значение функции
при х1=3 и х2=5.
• На сколько
отличается х1 от х2,
f(х1) от f(х2) ?
• Разность х1-х2=5-3=2
f
обозначим х
• Разность f(х1)f(х2)=0-4=-4
обозначим f
x

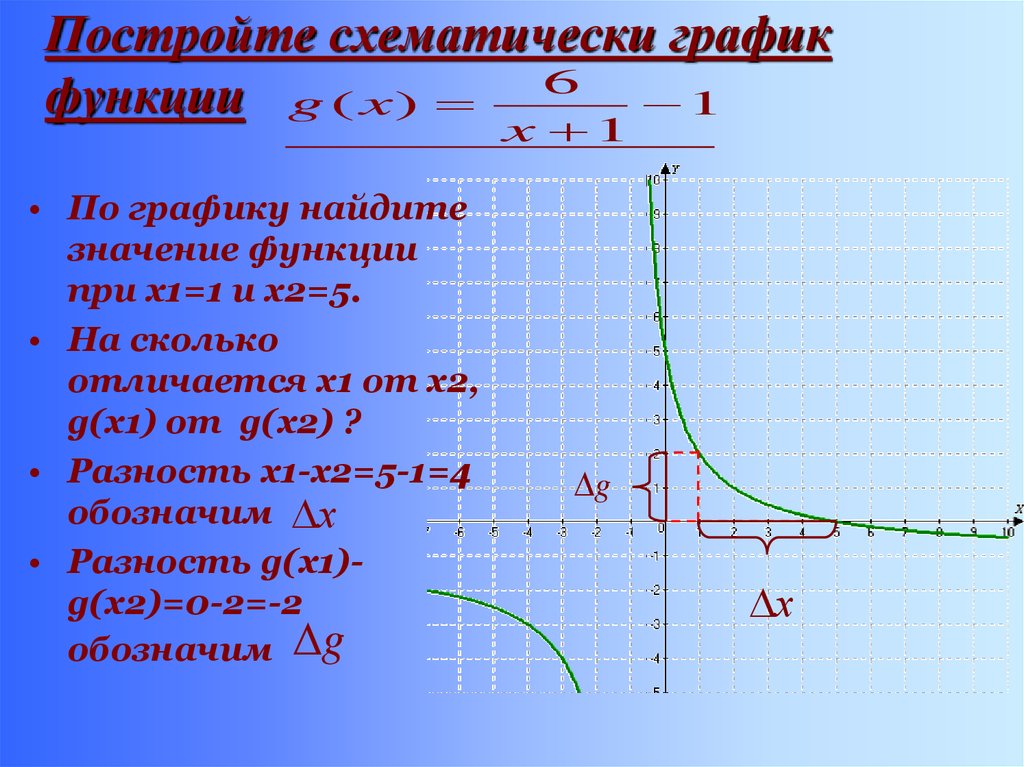
4. Постройте схематически график функции

g ( x) 6 1
x 1
• По графику найдите
значение функции
при х1=1 и х2=5.
• На сколько
отличается х1 от х2,
g(х1) от g(х2) ?
• Разность х1-х2=5-1=4
обозначим х
• Разность g(х1)g(х2)=0-2=-2
обозначим g
g
х

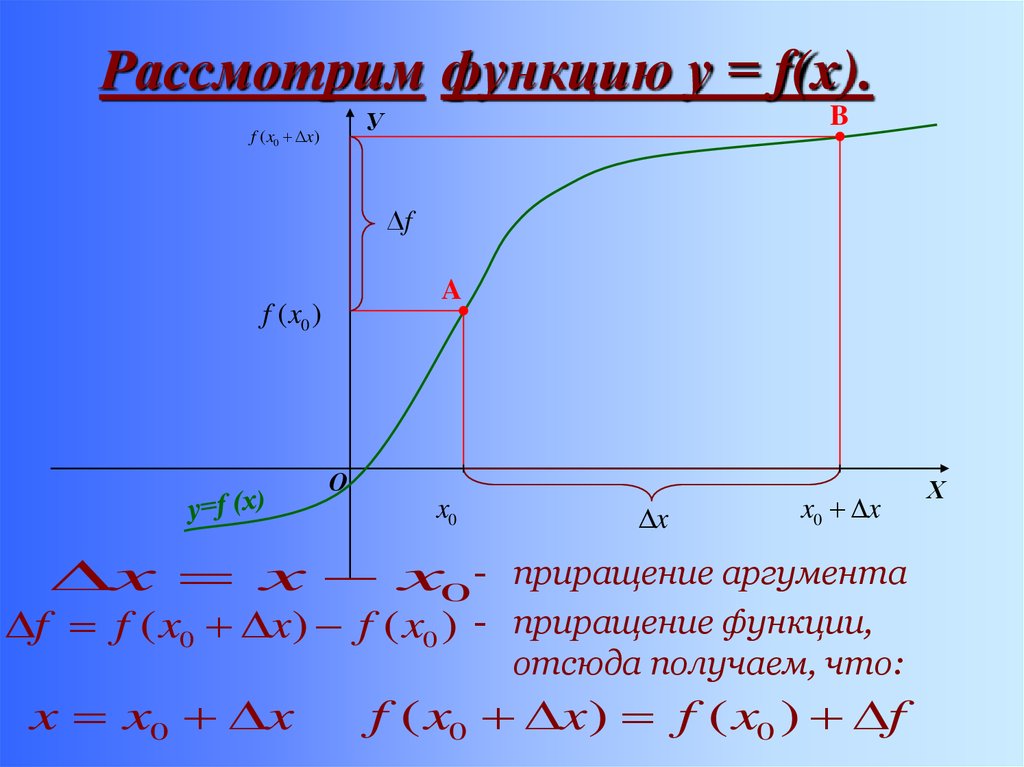
5. Рассмотрим функцию у = f(x).

B
У
f ( x0 x)
f
A
f ( x0 )
О
x0
x
x0 x
x x x0 -
приращение аргумента
f f ( x0 x) f ( x0 ) - приращение функции,
отсюда получаем, что:
x x0 x
f ( x0 x) f ( x0 ) f
Х

6. Пример 1.

• Найти приращение функции в точке х0, если
f ( x) 2 x 3, x0 3, x 0,2
2
Решение:
f ( x0 ) 2 * 3 3 15;
2
x x0 x 3 0.2 2.8;
f ( x) 2 * 2.8 3 12.68;
2
f f ( x0 x) f ( x0 ) 12.68 15 2.32

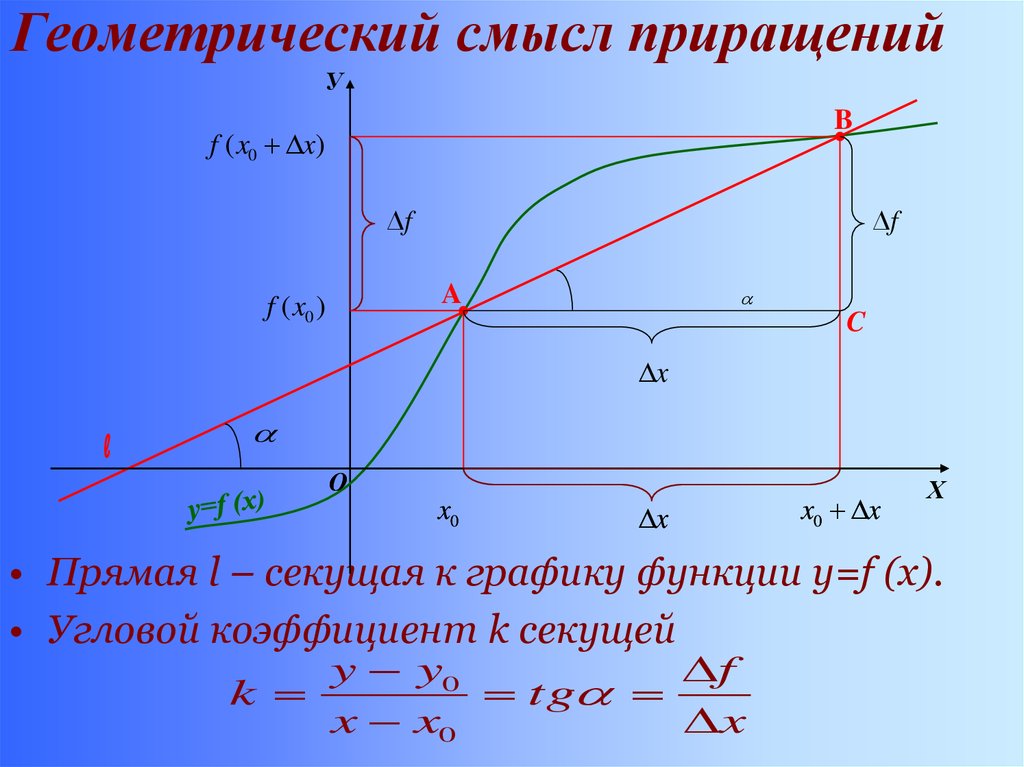
7. Геометрический смысл приращений

У
B
f ( x0 x)
f
f
A
f ( x0 )
C
x
О
x0
x
x0 x
Х
• Прямая l – секущая к графику функции y=f (x).
• Угловой коэффициент k секущей
y y0
f
k
tg
x x0
x

8. Пример 2.

• Найдите угловой коэффициент секущей к графику
функции f ( x) 0.5 x 2
проходящей через точки с данными абсциссами х1=0 и
х2=1. Какой (острый или тупой) образует секущая с
осью Ох?
Решение:
x x1 x2 1 0 1;
f ( x2 ) 0.5 *12 0.5;
f ( x1 ) 0.5 * 02 0;
y
0.5
k tg
0.5;
x
1
tg 0.5 0, значит острый угол.
Ответ : f 0.5; острый угол.

9. Ответьте на вопросы

• Что называется приращением
аргумента?
• Что называется приращением
функции?
• Что такое секущая?
• Чему равен угловой коэффициент
секущей?