Similar presentations:
Тема урока: Приращение функции
1. Тема урока:Приращение функции
2. Цели урока:
Формирование понятия приращенияфункции и приращения аргумента,
секущей, геометрического смысла
приращения функции;
Развитие вычислительных навыков;
Воспитание познавательного
интереса к предмету.
3.
Дан график функции у=4-х2По графику найти значение
функции в точке х1=1 и
х2=2
у
4
3
Разность х2 - х1=2-1=1; ∆x=1
2
∆f
f (1)=3; f(2)=0; f(2)- f(1)=0-3= -3
∆f=-3
1
-2
-1
0
1
2
∆x
х
4.
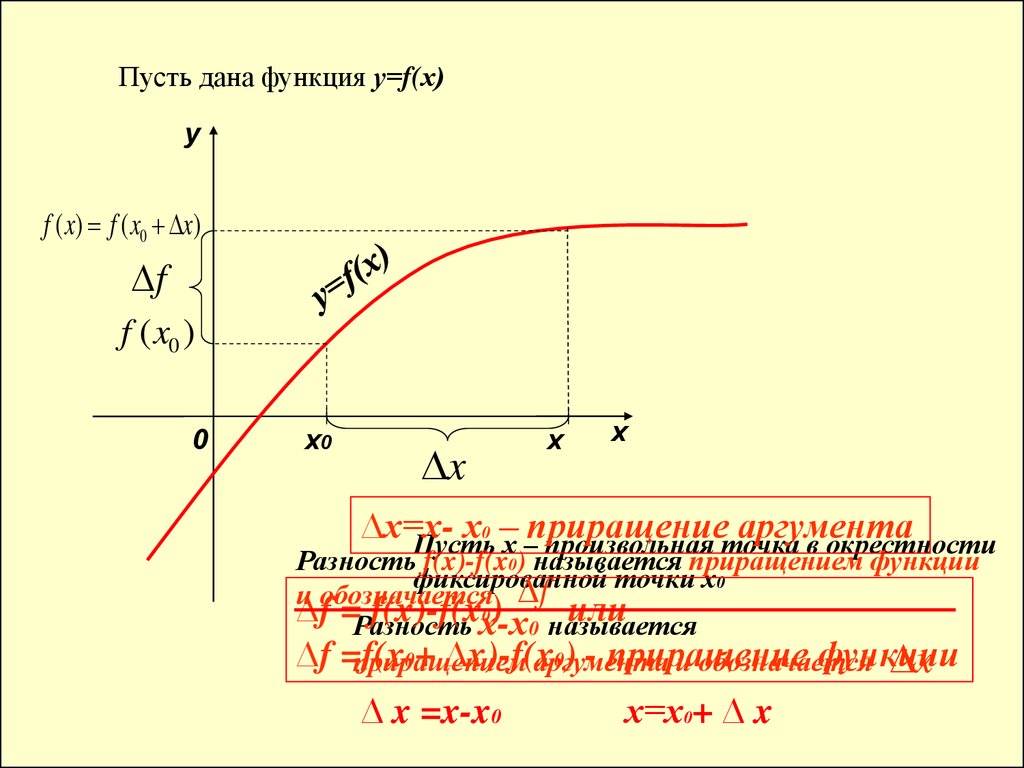
Пусть дана функция у=f(х)y
f ( x) f ( x0 x)
f
f ( x0 )
0
х0
x
х
x
∆х=хх0 – приращение аргумента
Пусть х – произвольная точка в окрестности
Разность f(x)-f(x0) называется приращением функции
фиксированной точки х0
и обозначается f
∆f =Разность
f(x)-f(xх-х
0)
или
0 называется
∆f =f(x
0+ ∆x)-f(x
0) - приращение
функции
приращением
аргумента
и обозначается
x
∆ x =x-x0
х=х0+ ∆ x
5.
Пример 1:Найти приращение аргумента и приращение
2
функции в точке х0, если
f ( x) x
x 1, 9
Решение:
x0 2
x x x0 ;
x 1, 9 2 0,1;
f f ( x) f ( x0 );
f f (1,9) f (2) 1,9 2 3,61 4 0,39
2
2
Ответ : x 0,1; f 0,39
6. Геометрический смысл приращения функции
Геометрический смысл приращенияy
функции
y=kх+b
В
f ( x) f ( x0 x)
f
f ( x0 )
0
А
х0
f
С
x
x
х
k tg
ABC - прямоугольный
x
BC
tg
AC
Прямая l , проходящая через
любые две точки графика функции,
-угловой коэффициент
называется секущей к графику
секущей к графику
функции.
функции
f
k tg
x
7.
№184( а )1 2
f ( x)
x ; x0 0; x 1
2
Решение :
tg
x x x0 ;
x 1 0 1;
1
k tg
2
f
;
x
f f ( x) f ( x0 );
1 2 1 2 1
f f (1) f (0) 1 0
2
2
2
0 острый
1
Ответ : tg ; острый
2
8.
№177(а)Дано: а=15м;
в=20м
Меньшую сторону увеличили на 0,11м
0,11
15 + 0,11=15,11м
а
Найти Р и S
Решение:
P = 2(a+b)
Р=Р-Р0
в
S=S - S0
S=ab
P0=2(15+20)=70м
S0=15 20=300м2
P=2(15,11+20)=70,22м
S=15,11 20=302,2 м2
Ответ:∆P=0,22м; ∆S=2,2м2
Р=70,22-70=0,22м
S=302,2-300=2,2м2







 mathematics
mathematics








