Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника

1.

ПЕРПЕНДИКУЛЯР К ПРЯМОЙ.
МЕДИАНЫ, БИССЕКТРИСЫ И
ВЫСОТЫ ТРЕУГОЛЬНИКА.

2.

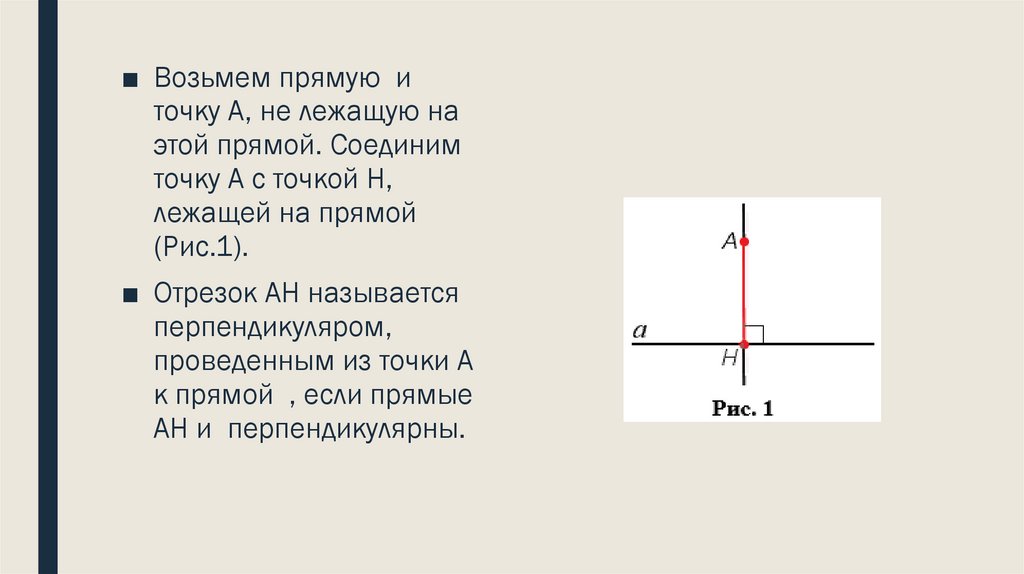
■ Возьмем прямую и
точку А, не лежащую на
этой прямой. Соединим
точку А с точкой Н,
лежащей на прямой
(Рис.1).
■ Отрезок АН называется
перпендикуляром,
проведенным из точки А
к прямой , если прямые
АН и перпендикулярны.

3.

■ Перпендикулярные прямые — две прямые,
которые пересекаются под прямым углом.
■ Две прямые на плоскости называются
перпендикулярными, если при пересечении
образуют 4 прямых угла.

4.

ТЕОРЕМА.
■Из точки, не лежащей на
прямой, можно провести
перпендикуляр к этой прямой,
и притом только один.

5.

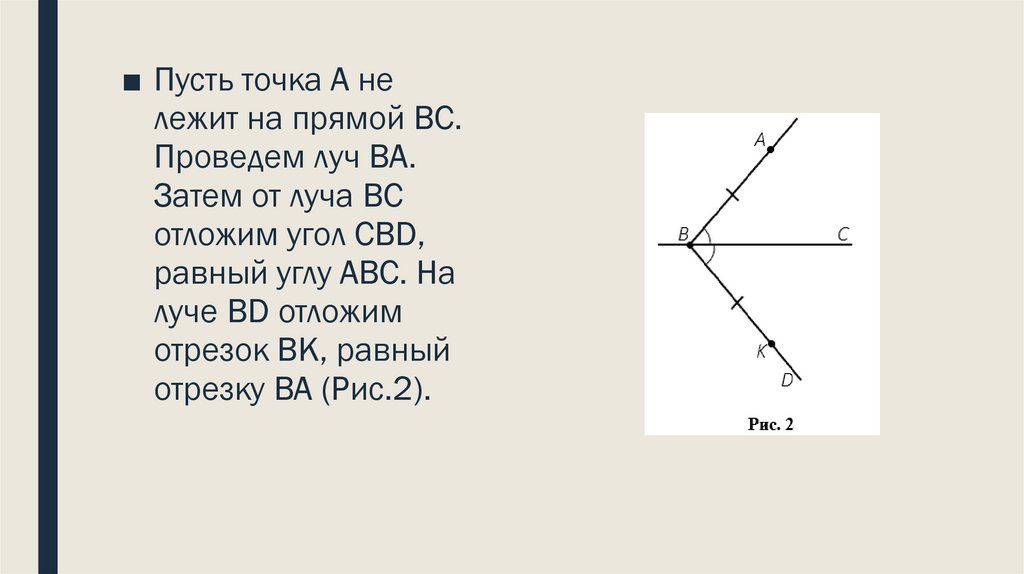
■ Пусть точка А не
лежит на прямой ВС.
Проведем луч ВА.
Затем от луча ВС
отложим угол СВD,
равный углу АВС. На
луче ВD отложим
отрезок ВК, равный
отрезку ВА (Рис.2).

6.

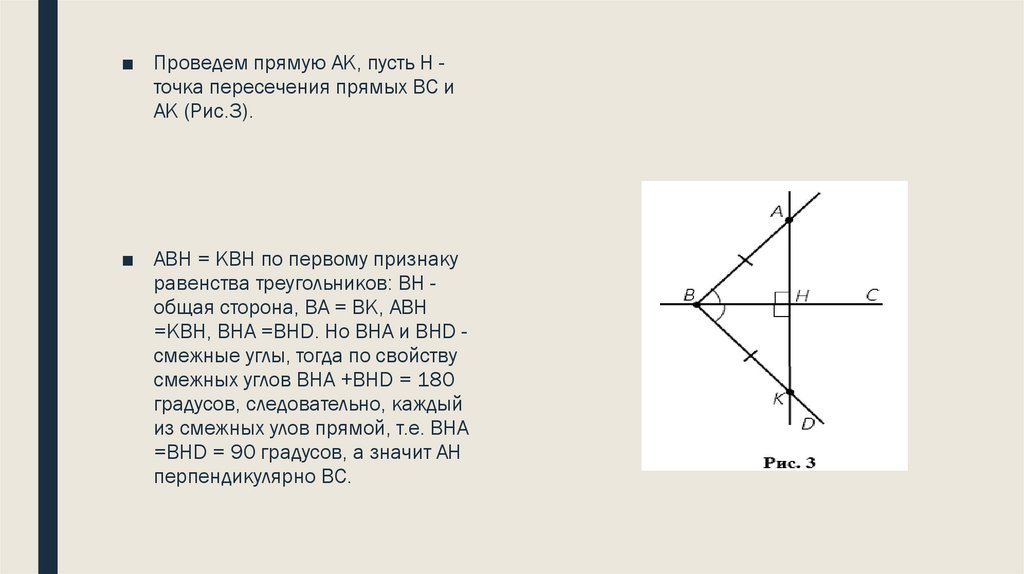
■ Проведем прямую АК, пусть Н точка пересечения прямых ВС и
АК (Рис.3).
■ АВН = КВН по первому признаку
равенства треугольников: ВН общая сторона, ВА = ВК, АВН
=КBН, ВНА =ВНD. Но ВНА и ВНD смежные углы, тогда по свойству
смежных углов ВНА +ВНD = 180
градусов, следовательно, каждый
из смежных улов прямой, т.е. ВНА
=ВНD = 90 градусов, а значит АН
перпендикулярно ВС.

7.

■ Предположим, что через
точку А можно провести еще
один перпендикуляр АН1 к
прямой ВС, тогда получим,
что две прямые АН и АН1,
перпендикулярные к прямой
ВС пересекаются в точке А
(Рис.4). Но по свойству
перпендикулярных прямых,
прямые АН и АН1
пересекаться не могут,
значит, наше предположение
неверно и через точку А
можно провести только один
перпендикуляр к прямой ВС.

8.

■ Для проведения перпендикуляра
из точки к прямой, используют
чертежный угольник (Рис.5).
Чертежный угольник
прикладывают так, чтобы одна из
его сторон, образующих прямой
угол угольника, располагалась
вдоль прямой, к которой нужно
провести перпендикуляр

9.

МЕДИАНЫ,
БИССЕКТРИСЫ И
ВЫСОТЫ ТРЕУГОЛЬНИКА.

10.

■Медиана треугольника — это
отрезок, соединяющий
вершину треугольника с
серединой противолежащей
стороны.

11.

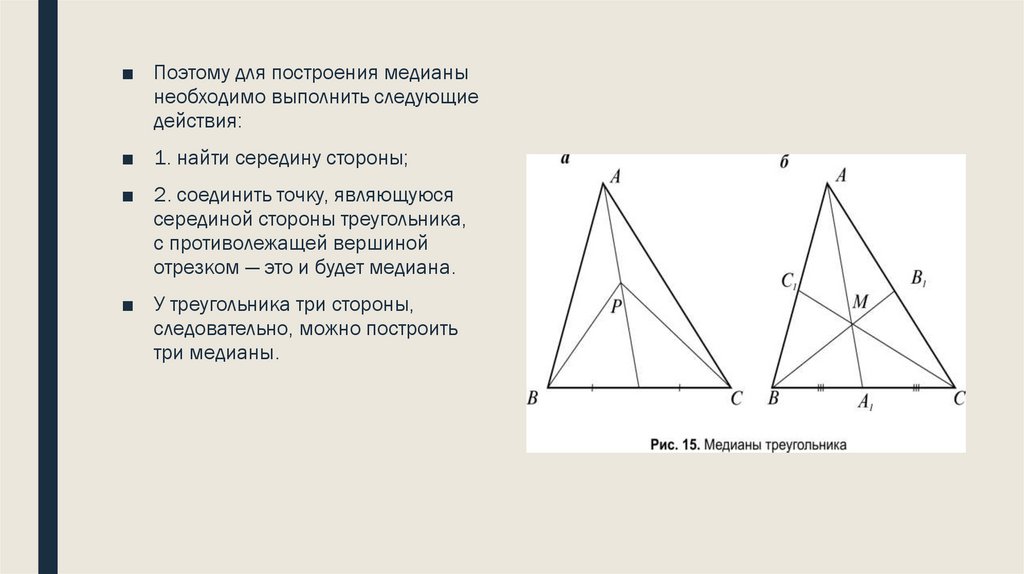
■ Поэтому для построения медианы
необходимо выполнить следующие
действия:
■ 1. найти середину стороны;
■ 2. соединить точку, являющуюся
серединой стороны треугольника,
с противолежащей вершиной
отрезком — это и будет медиана.
■ У треугольника три стороны,
следовательно, можно построить
три медианы.

12.

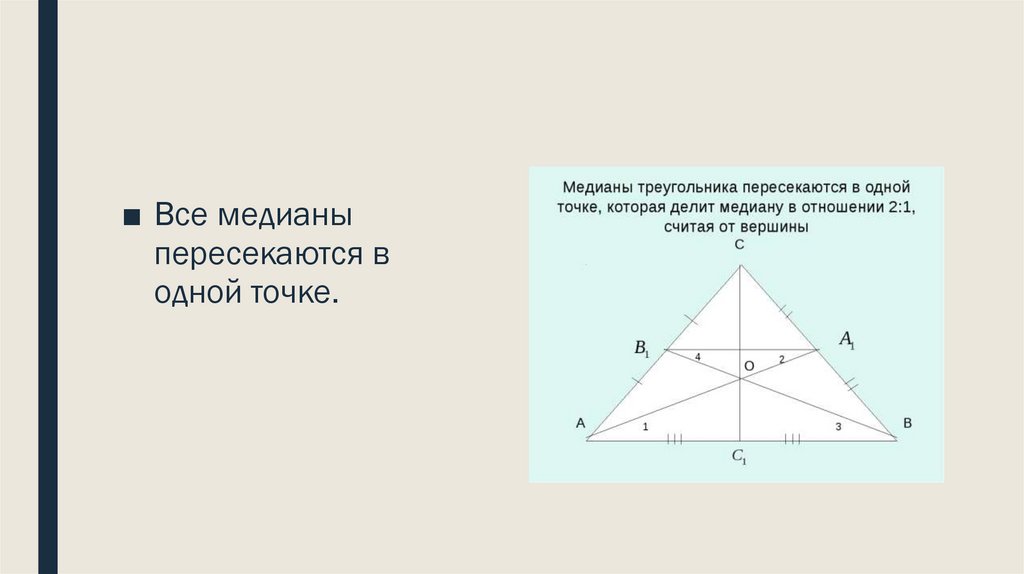
■ Все медианы
пересекаются в
одной точке.

13.

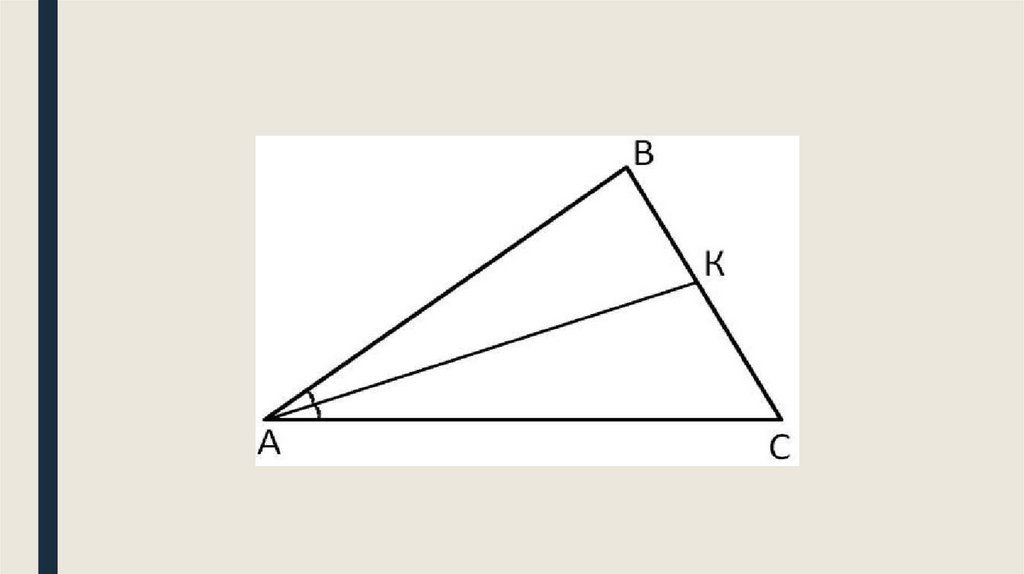
Биссектриса треугольника — это отрезок
биссектрисы угла треугольника,
соединяющий вершину с точкой на
противоположной стороне.
У треугольника три угла и три
биссектрисы.
Все биссектрисы пересекаются в одной
точке.

14.

15.

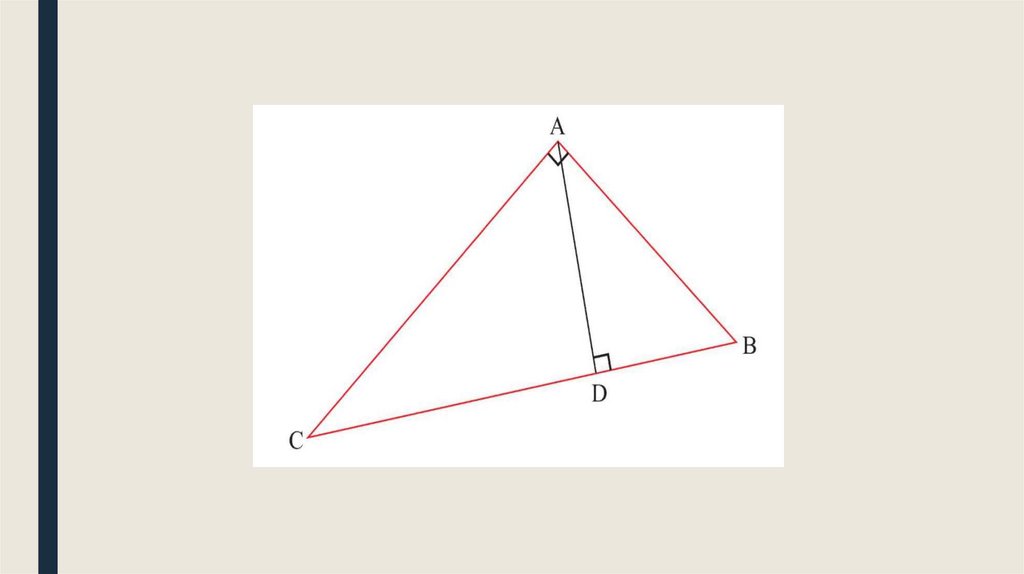
Высота треугольника — это перпендикуляр,
опущенный из вершины треугольника к
прямой, содержащей противоположную
сторону.
Так же как медианы и биссектрисы,
треугольник имеет три высоты.
Высоты треугольника пересекаются в
одной точке.

16.

17.

ОБРАТИ ВНИМАНИЕ!
■Если из одной и той же вершины
провести медиану, биссектрису и
высоту, то медиана окажется самым
длинным отрезком, а высота —
самим коротким отрезком.