Similar presentations:
Простейшие показательные и логарифмические уравнения и неравенства
1. Простейшие показательные и логарифмические уравнения и неравенства Выполнила: Есаян А.А. Учитель математики МАОУ СОШ №20
2. Цель урока:
Обобщение и систематизация знаний,умений и навыков по теме: «Простейшие
показательные и логарифмические
уравнения и неравенства».
3. План:
1.2.
3.
4.
5.
Простейшие показательные уравнения
Простейшие логарифмические уравнения
Простейшие показательные неравенства
Простейшие логарифмические неравенства
Тест
4. 1. Простейшие показательные уравнения
Дайте определение простейшегопоказательного уравнения
Ответ
5.
Уравнение вида a b , где a 0 , a 1называется простейшим показательным
уравнением.
x
6. Что является решением уравнения ? Ответ
Что является решением уравненияx
a b ?
Ответ
7.
При b 0 уравнение не имеетрешений
При b 0 уравнение имеет
единственный корень x log a b
8. Решите уравнения 1. Ответ: 2. Ответ: 3. Ответ:
Решите уравнения1.
2 4
Ответ: 2
2.
3 5
Ответ: log 3 5
x
x
3. 5 1
x
Ответ: нет
решений
9.
2. Простейшие логарифмическиеуравнения
Назовите вид простейшего
логарифмического уравнения
Ответ
10.
Уравнение вида log a x b ,где a 0 , a 1 , x 0
называется простейшим
логарифмическим уравнением.
11. Что является решением уравнения ?
Что является решениемуравнения log a x b ?
Ответ: x
a
b
12. Решите уравнения 1. Ответ: 2. Ответ: 3. Ответ:
Решите уравнения1. log 3 x 2
Ответ: 9
2. log 1 x 3
Ответ: 8
2
3. log 5 x 0
Ответ: 1
13. 3. Простейшие показательные неравенства
14. Назовите виды простейших показательных неравенств
a ba b
a b
a b
x
x
x
x
Какие значения принимает a?
a 0, a 1
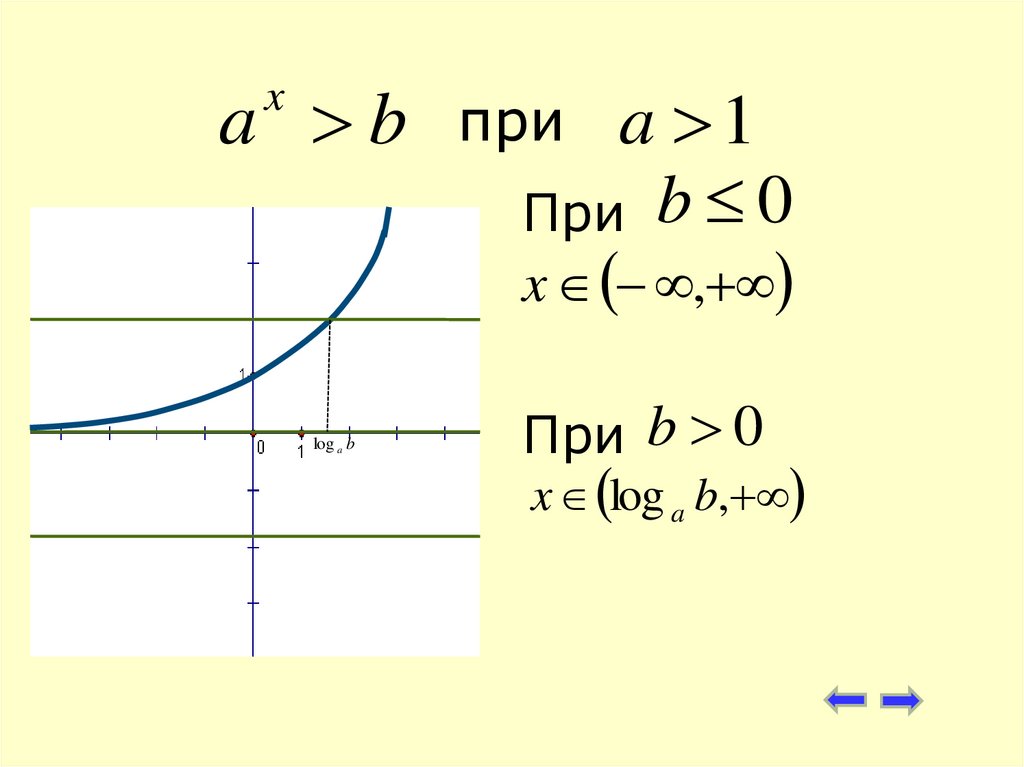
15. Решим неравенство графическим методом При При
Решим неравенство aграфическим методом
При
a 1
При 0 a 1
x
b
16. при
a bx
log a b
a 1
При b 0
x ,
при
При b 0
x log a b,
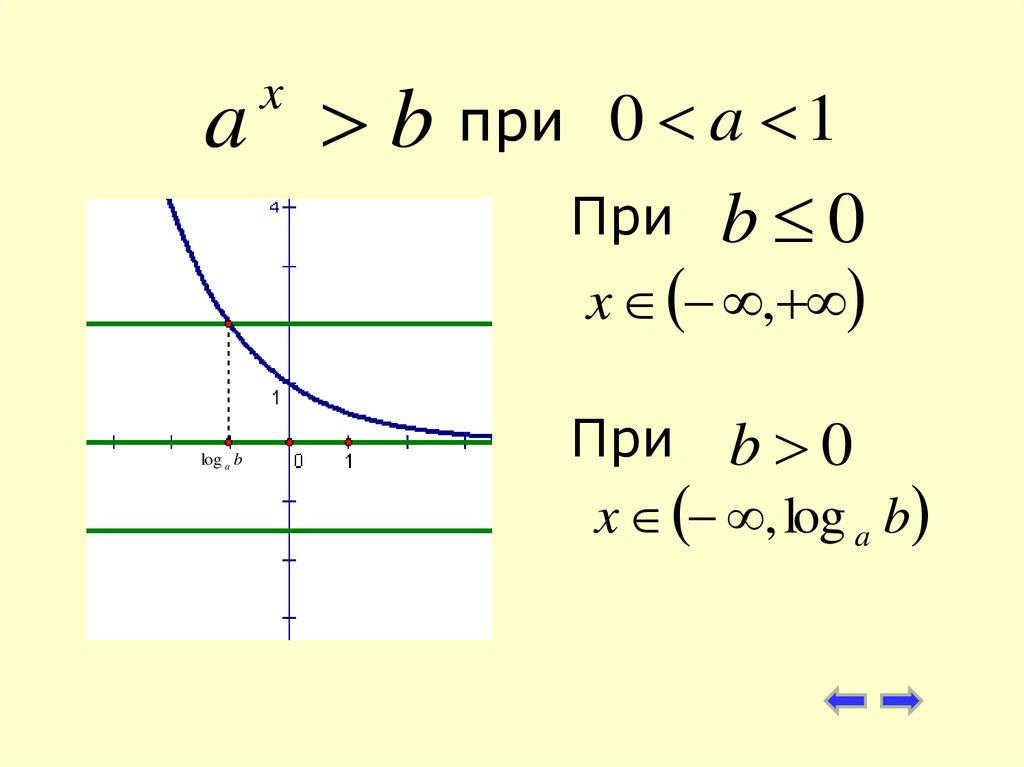
17. при
a b приx
0 a 1
b 0
x ,
При
log a b
При b 0
x , log a b
18.
Аналогично решаетсяx
неравенство a b
19. При При При При
a bx
a 1
При
b 0
0 a 1
При b 0
нет решений
нет решений
При b 0
При b 0
x , log a b
x log a b,
20. Решите неравенства 1. Ответ: 2. Ответ: 3. Ответ: 4. Ответ:
Решите неравенства1. 2 8
x
2. 51 0
2
3. 7
x
4. 11 1
x
x
Ответ: ,3
Ответ: ,
Ответ:нетрешений
Ответ: 0,
21.
1. 2 8x
2 2
x
3
Т.к. 2>1, то функция y 2 возрастает.
t
x 3
Ответ: ,3
22.
2. 5 0x
Т.к. 5 0 , то x , .
Ответ: ,
x
23.
x1
2
7
x
1
0
7
3.
Т.к.
, то
неравенство не имеет
решений.
Ответ: нет решений.
24.
4. 11 1x
11 11
x
0
Т.к. 11>1, то функция y 11 возрастает.
t
x 0
Ответ: 0,
25. 4. Простейшие логарифмические неравенства
26. Какие виды простейших логарифмических неравенств Вы знаете?
log a x blog a x b
log a x b
log a x b
При каких условиях
неравенства имеют решения?
a 0, a 1, x 0
27. Решим неравенства и графическим методом
Решим неравенства log a x b иlog a x b графическим методом
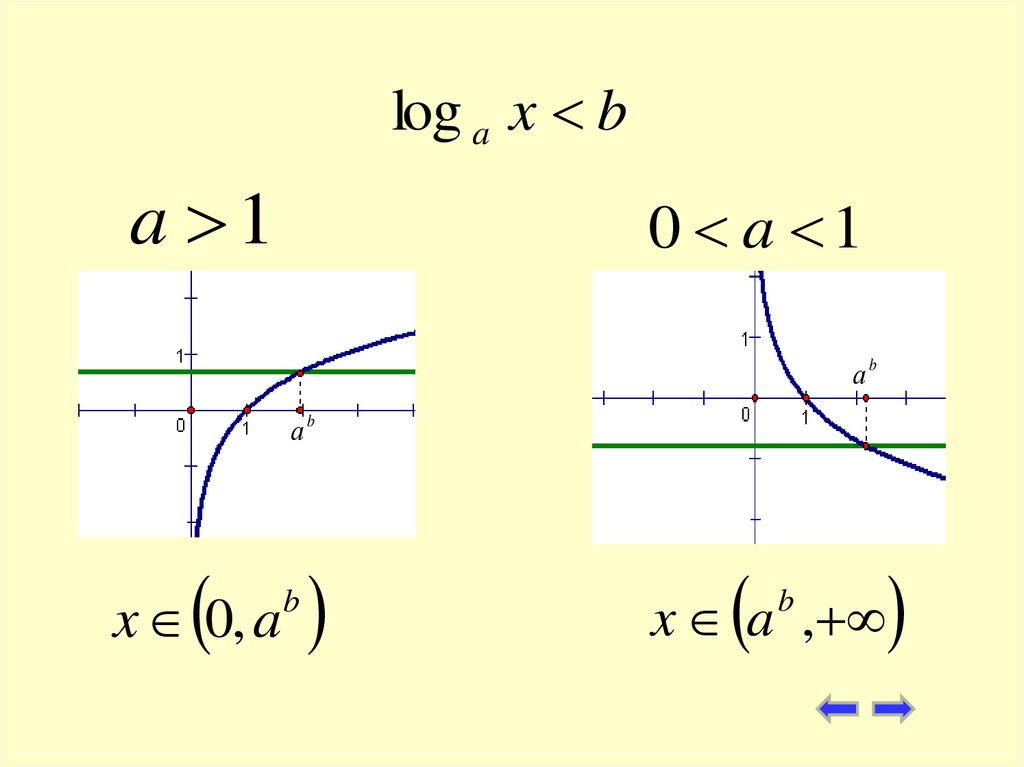
28.
log a x ba 1
0 a 1
аb
аb
x a ,
b
x 0, a
b
29.
log a x ba 1
0 a 1
аb
аb
x 0, a
b
x a ,
b
30. Решите неравенства 1. Ответ: 2. Ответ:
Решите неравенства1. log 2 x 5
Ответ:(32, )
2. log 1 x 1
Ответ: 5,
5
31.
1. log 2 x 5log 2 x log 2 32
Т.к. 2>1, то функция
- возрастает.
x 0
x 32
X>32
Ответ: (32, )
y log 2 t
32.
2. log 1 x 15
log 1 x log 1 5
5
5
1
Т.к. 0 5 1 , то функция y log 1 t
5
убывает.
x 0
x 5
x 5
Ответ: 5,
33. 5. Тест
34.
1. Выберите промежуток,которому принадлежит корень
уравнения 2 x 1 2 x 1 10
2;
0;2
; 2
2;2
35.
Отвечайте на следующий вопрос!36.
Подумайте ещё!37. 2. Чему равно произведение корней уравнения ?
2. Чему равно произведениекорней уравнения lg 2 x lg x 2 0 ?
1
10
10
10
1
10
38.
Отвечайте на следующий вопрос!39.
Подумайте ещё!40.
3. Выберите промежуток,который является решением
28
x
x 3
неравенства 3 3
9
1;
;1
1;
0;1
41.
Отвечайте на следующий вопрос!42.
Подумайте ещё!43. 4. Выберите промежуток, являющийся решением неравенства
log 1 (2 x 1) 00;
;0
2
0;
0;1
44.
Тестирование завершено!45.
Подумайте ещё!46. Презентацию подготовили: Быкова С.В. Кузнецова О.А. Кокорина Л.Н.
47. Литература
Никольский С. М., Потапов М. К., Решетников Н. Н.,Шевкин А. В. Алгебра и начала анализа: Учебник
для 10-11 кл. М.: Просвещение, 2002.
















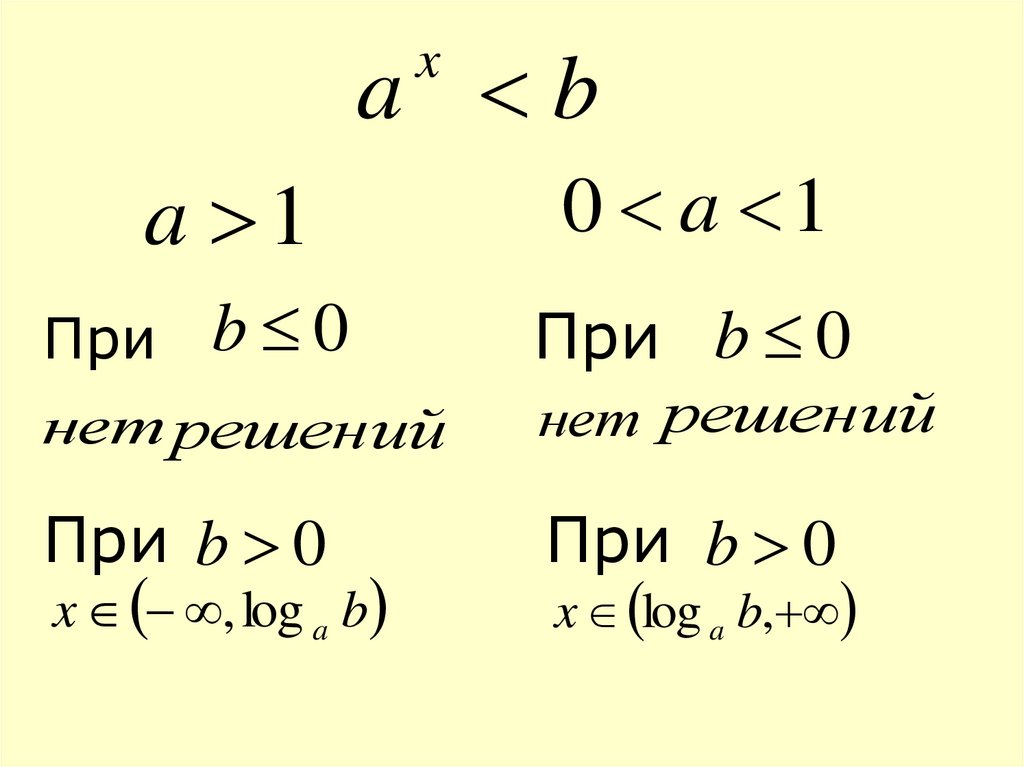



























 mathematics
mathematics








