Similar presentations:
Дифференциальные уравнения
1.
Формы записи дифференциального уравнения 1-го порядка:y = f ( x; y ) явная,
F ( x; y; y ) = 0 - общего вида
M ( x; y) dx N ( x; y) dy = 0 дифференциальная.
Например:
y = y 2 2 y явная,
x 2 y 2 xy 1 = 0 неявная,
( x 2 y 2 )dy (2 xy 1) dx = 0 дифференциальная.
Нахождение решения дифференциального уравнения
называется его интегрированием
Метод решения уравнения определяется типом уравнения.
2.
Уравнение с разделенными переменными – это уравнение видаf ( x) dx g ( y) dy = 0,
множителем при dx является функция
является функция y.
x, а множителем при dy
Решение таких уравнений заключается в почленном интегрировании
левой и правой его частей
f ( x) dx g ( y) dy = C.
1. cos x dx = y dy.
cos x dx = y dy.
sin x C =
2 3/2
3
y , y = [ (sin x C )]2/3 .
3
2
3.
Уравнения с разделяющимися переменнымиy' f1( x) f 2 ( y )
P1 ( x)P2 ( y )dx Q1 ( x)Q2 ( y )dy 0
1) Найти общее решение
дифференциального уравнения:
dy
cos x
dx ( y 3)2
cos x
y'
( y 3) 2
cos x
2
dx
(
y
3
)
dy cos xdx
dy
2
( y 3)
( y 3) dy cos xdx
2
y 3 3 sin x C 3
1
( y 3)3 sin x C
3
в явном виде
общий интеграл
4.
Уравнения с разделяющимися переменными2) Найти общее решение дифференциального уравнения:
x 1 y 2 dx y 1 x 2 dy 0
y 1 x dy x 1 y dx
2
y
2
x
1 y dy 1 x dx
2
y C 1 x
2
2
1
2
y
1 y
2
dy
x
1 x
2
dx
1 y2 1 x2 C
общий интеграл
в явном виде
5.
3. 6 xdx 6 ydy = 3x 2 ydy 2 xy 2dx.1) Собираем слагаемые с dx одну часть уравнения, а слагаемые с
dy в другую.
6 xdx 2 xy 2 dx=6 ydy 3x 2 ydy,
2) Выносим
dx и dy
3) Выносим
2x
и
3y
за скобки. (6 x 2 xy )dx = (6 y 3x y )dy,
2
2
за скобки и получаем
2 x (3 y 2 ) dx = 3 y (2 x 2 ) dy,
делим на произведение (2 x 2 ) (3 y 2 ) т.е. функций,
«стоящих не у своих дифференциалов», и интегрируем
2x
3y
2x
3y
dx =
dy,
dx =
dy,
2
2
2
2
2 x
3 y
2 x
3 y
3
ln | x 2 2 |= ln | 3 y 2 | ln C.
x2 2 = C
2
Ответ:
(3 y 2 )3 .
6.
Рассмотрим пример нахождения частного решения уравненияпо заданному начальному условию.
Решить задачу Коши y 2 y y 2 = 0, y (0) = 1/4.
1) Находим сначала общее решение уравнения:
y = y 2 2 y ,
dy
= ( y 2 2 y ),
dx
dy
= dx,
2
y 2y
dy
1 y 2
1
y 2 2 y = dx, 2 ln y = x 2 ln C.
Общее решение
y 2
= Ce2x .
y
2
1 = Ce2 x ,
y
2
= 1 Ce2 x ,
y
2) Определим значение константы C , исходя из начального условия.
Подставим в общее решение значения x = 0, y = 1/4.
1/4 2
= C e 0 , 9 = C.
1/4
3) Полученное значение C , подставляем в выражение для общего
2
решения и записываем
частное решение:
= 1 9e2 x .
y
7.
(1 y 2 )dx y 1 x 2 dy 08.
yy
0
1 x
9.
( x xy2 )dx ( y x 2 y )dy 010.
y e x y11.
xdy ydx y 2 dx12.
y 2 xy 0, y(0) 2.13.
tgydx – ctgxdy = 014.
(1 e x ) yy e x15.
y tgx y 2 3 y 216.
yyey 0
x
17.
y 2 sin y cos x 018.
yln y
y
у(2) = 1






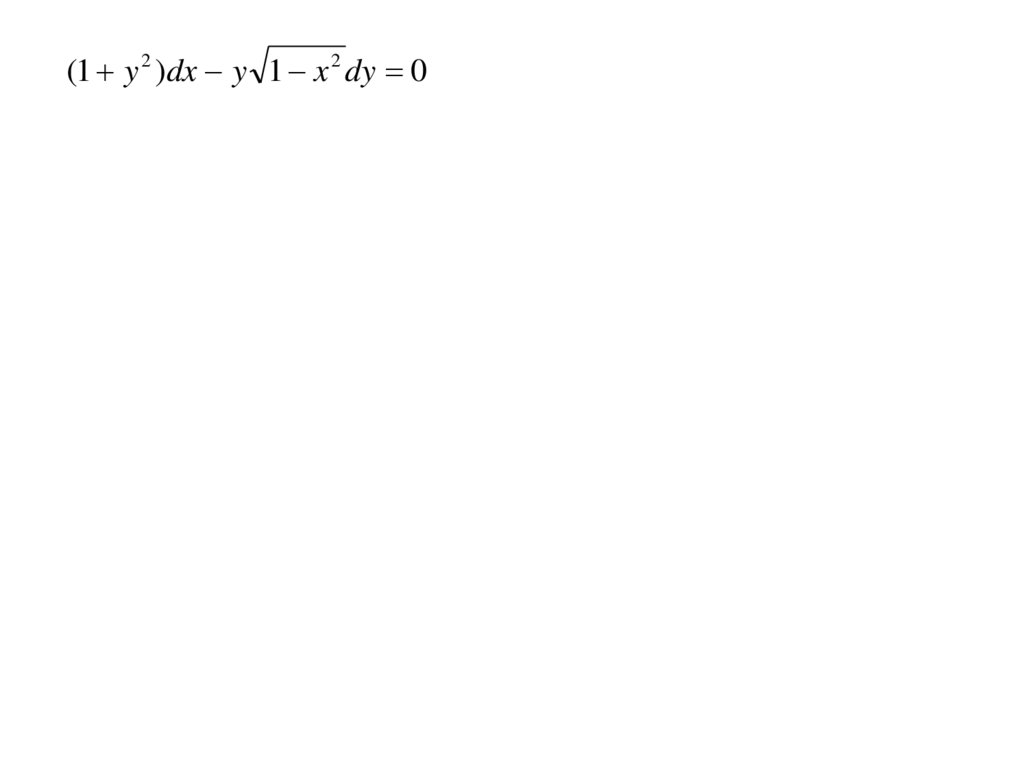
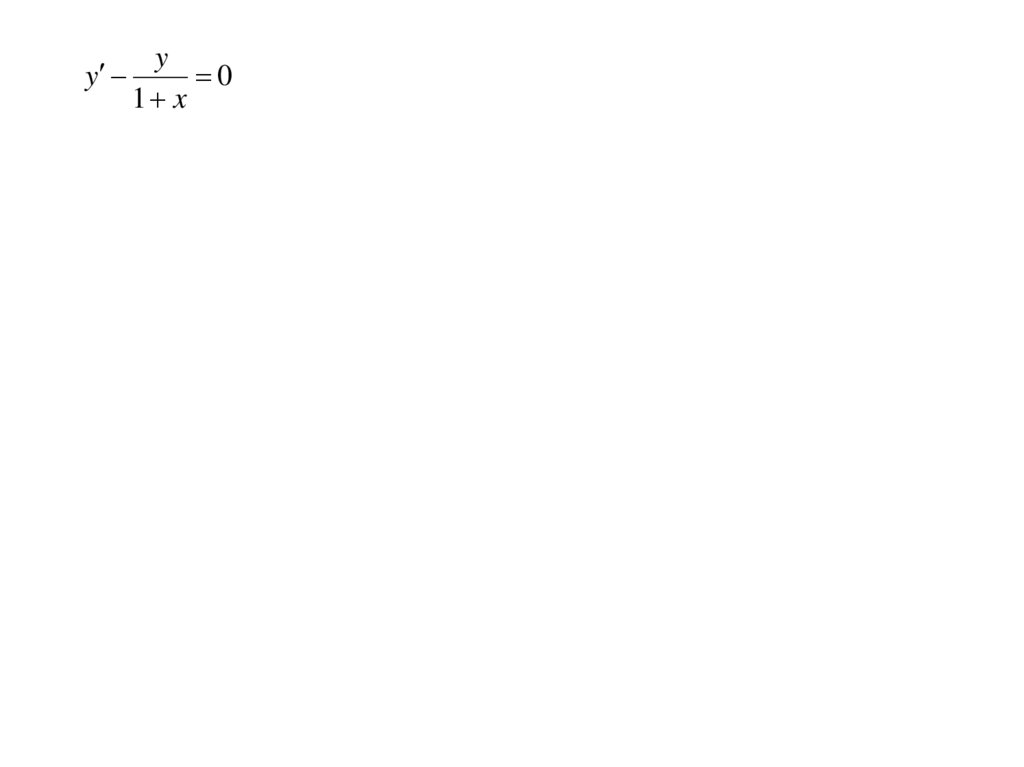
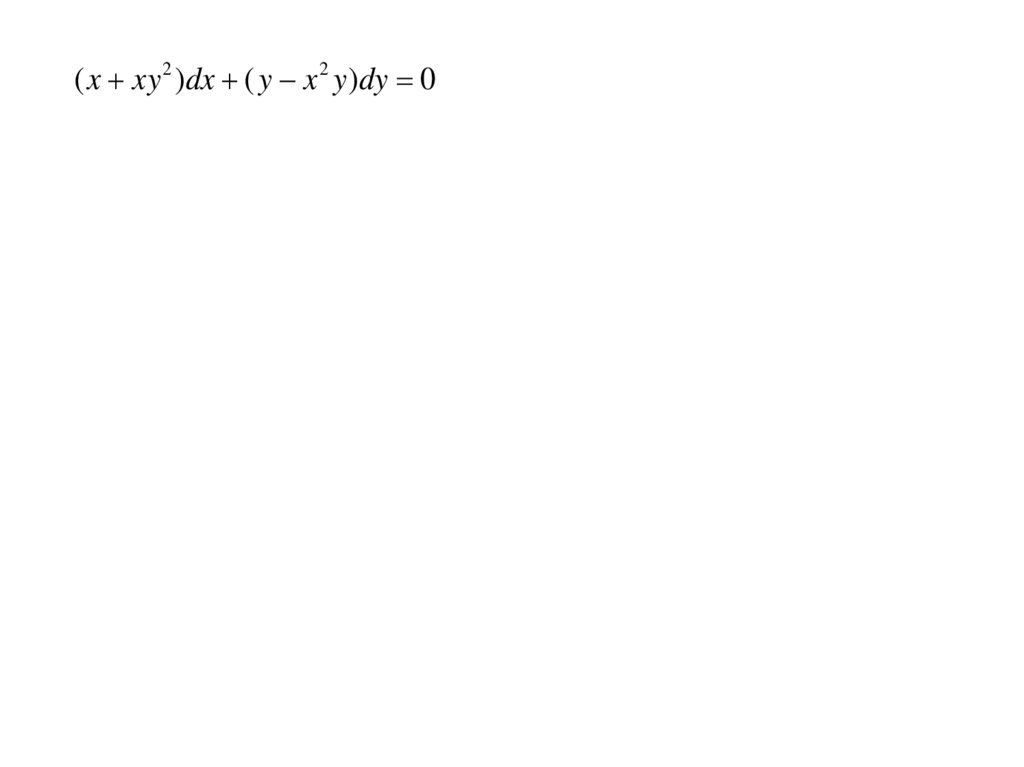
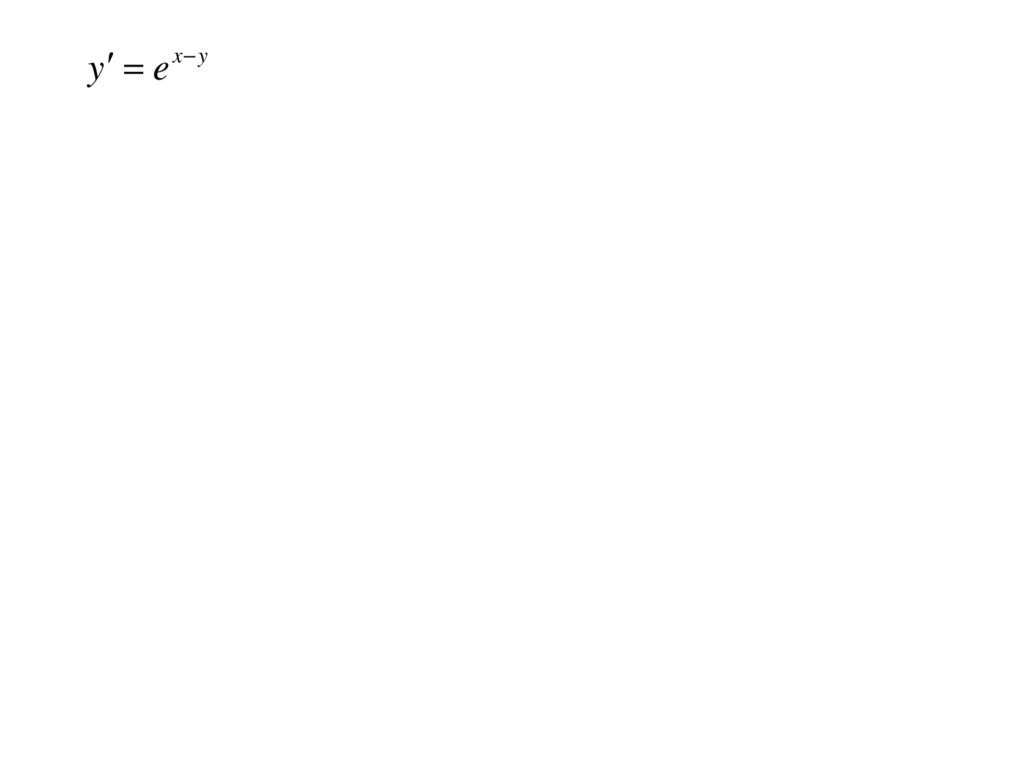
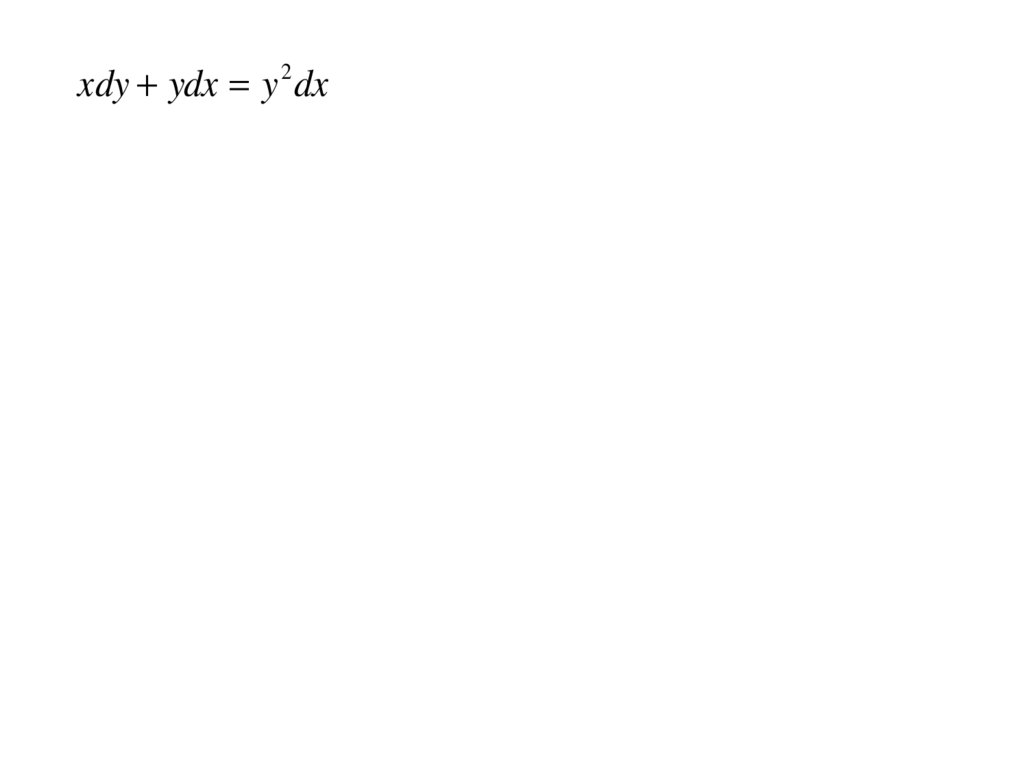
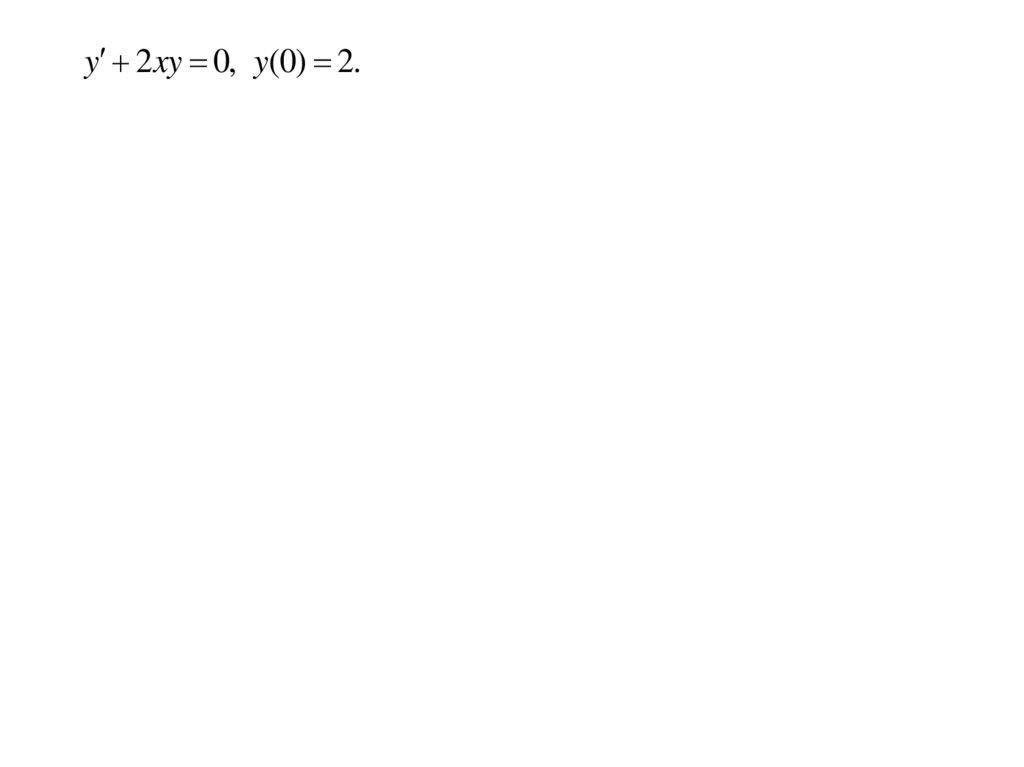

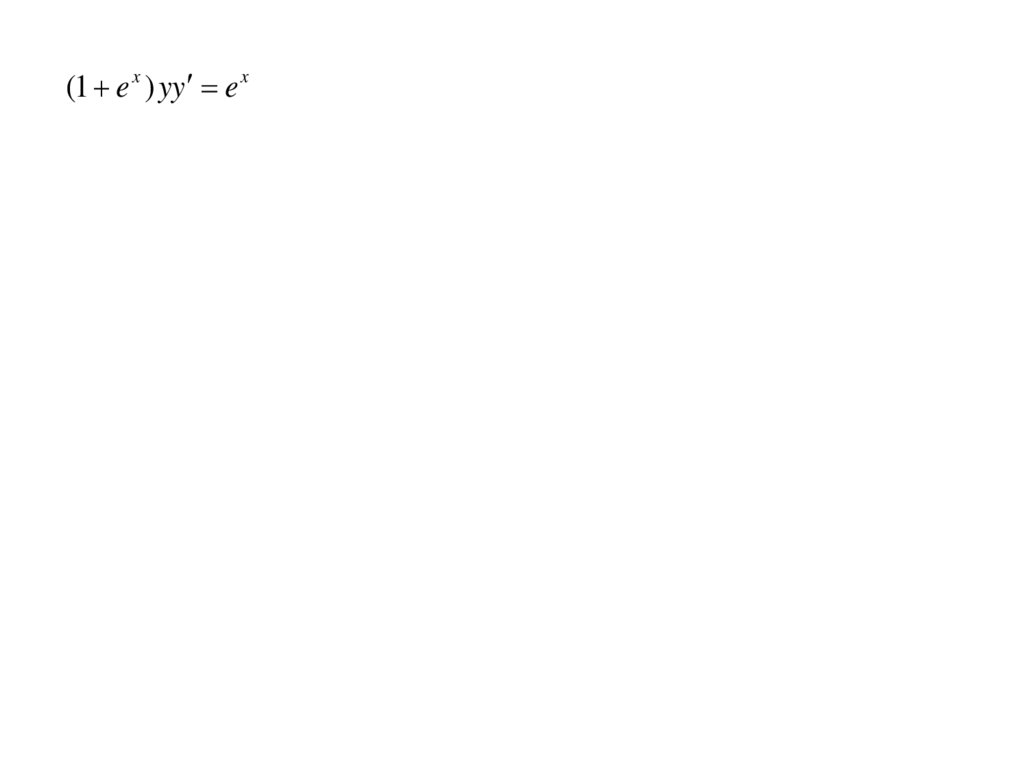
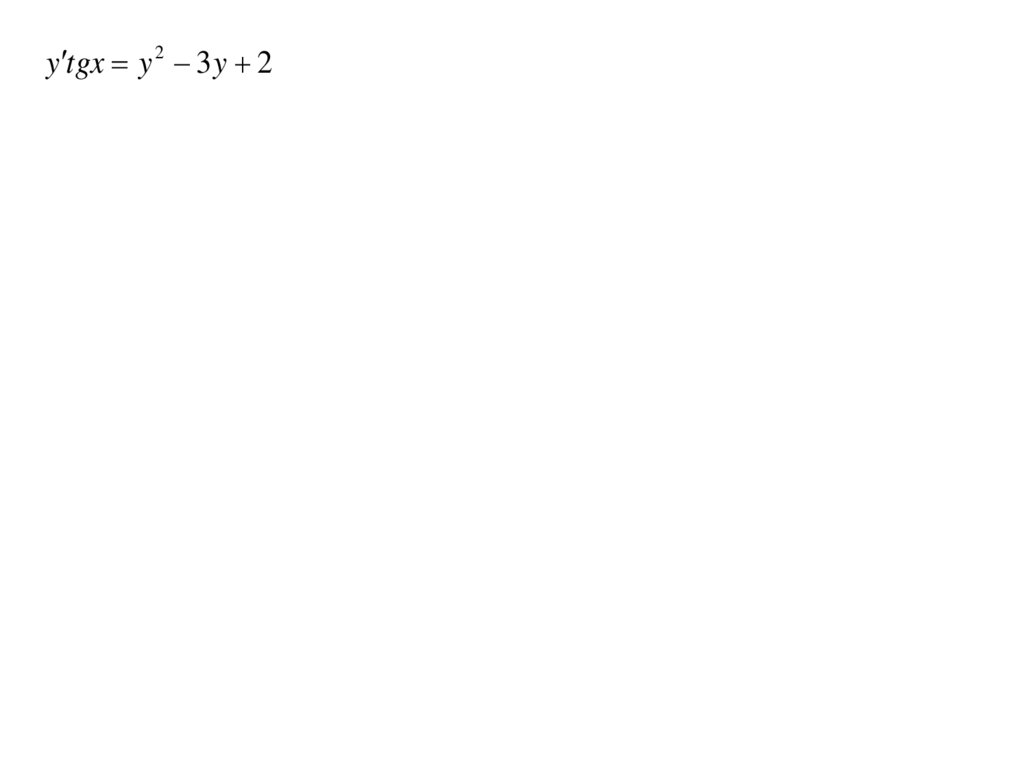
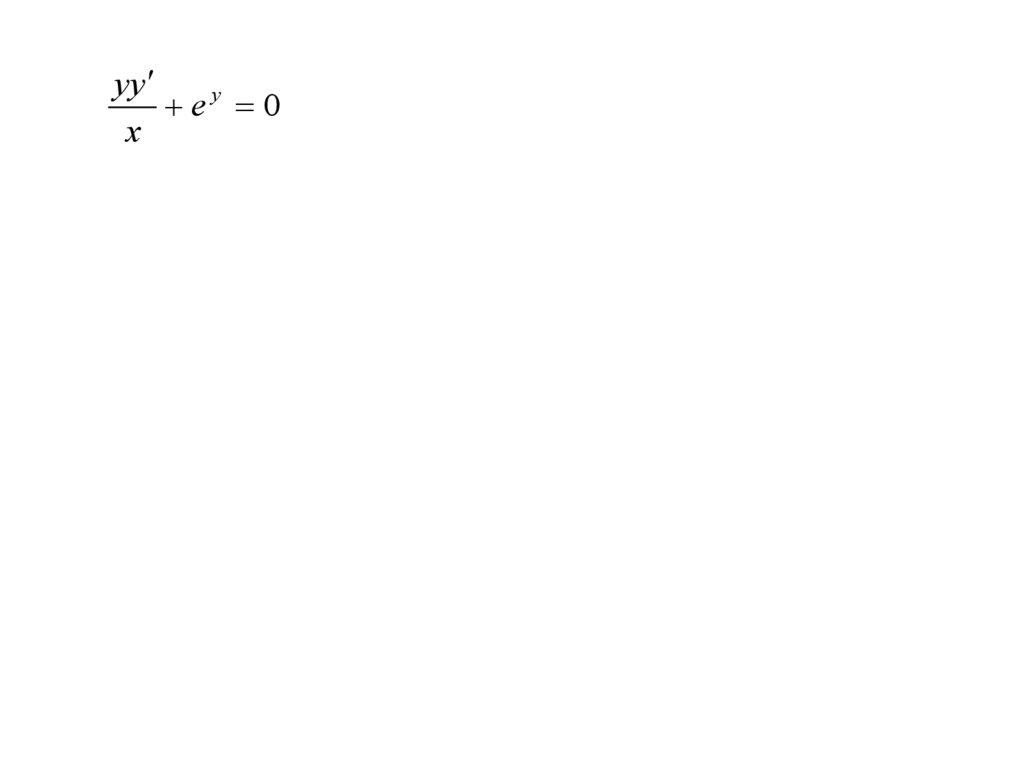
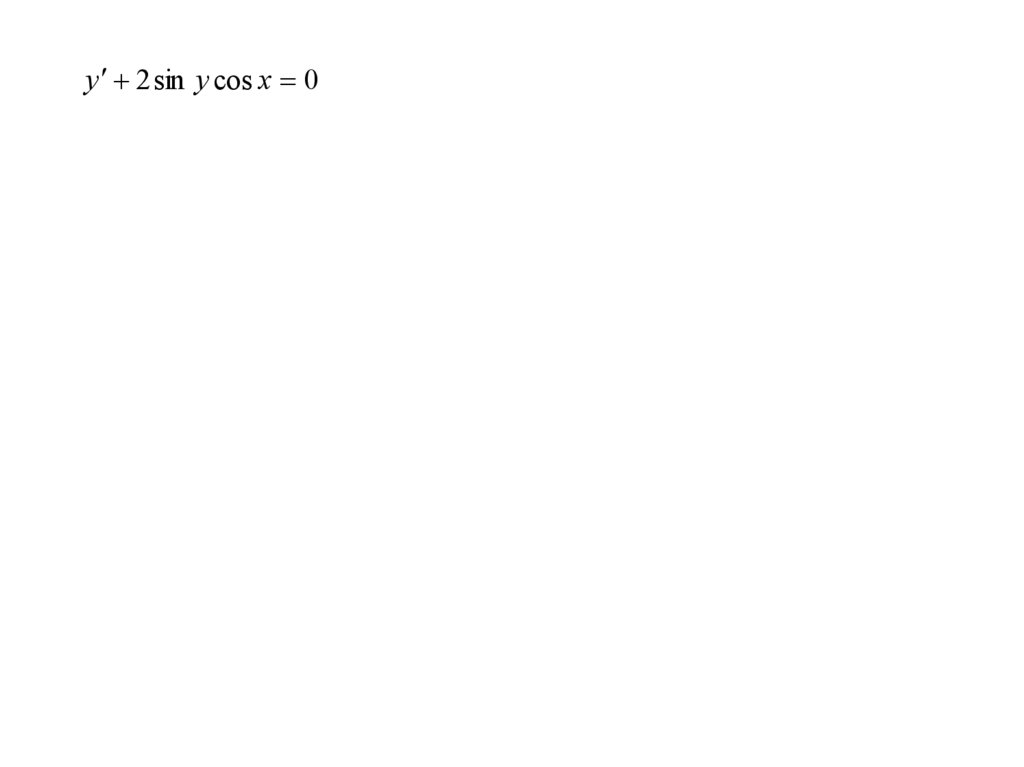

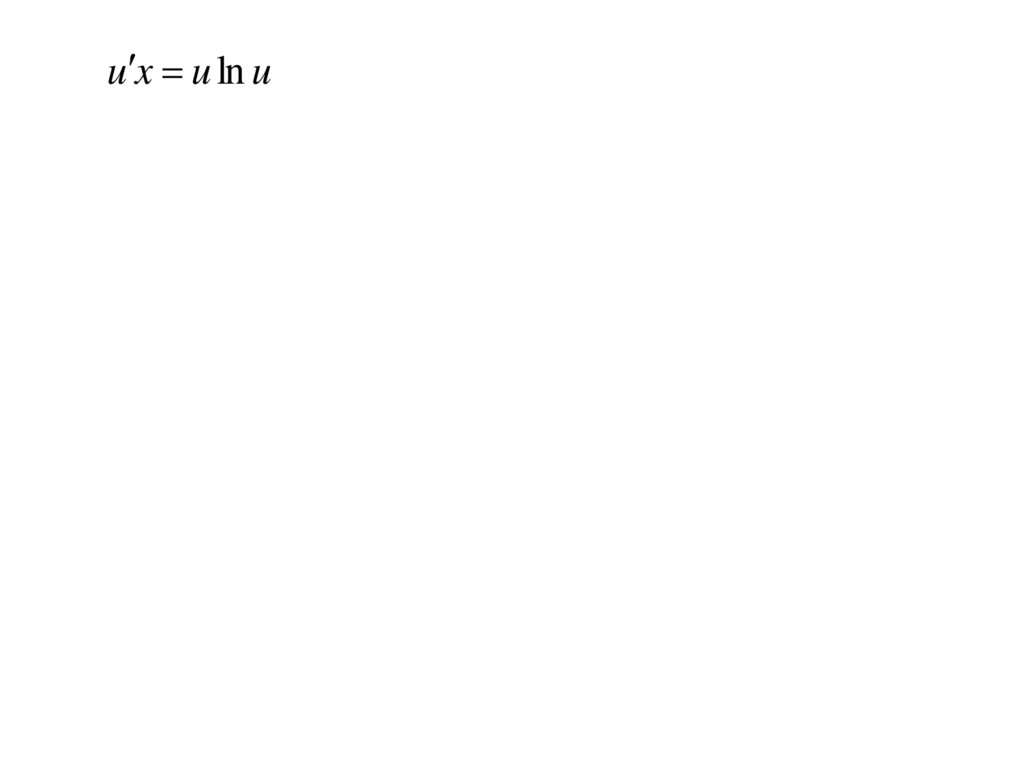
 mathematics
mathematics








