Линейная алгебра. Определители второго порядка. Определители n – ого порядка. Методы вычисления определителей

1. Линейная алгебра

Определители второго порядка
Определители n – ого порядка
Методы вычисления определителей

2. Определители 2 порядка

Определители широко применяются во многих разделах
высшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12a21
a 21 a 22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя

3. Определители n – ого порядка

Определителем n – ого порядка называется число:
a11 a12
a21 a 22
an1 an 2
a1n
a 2n
ann
Методы вычисления определителей n – ого порядка рассмотрим
на примере вычисления определителей третьего порядка.

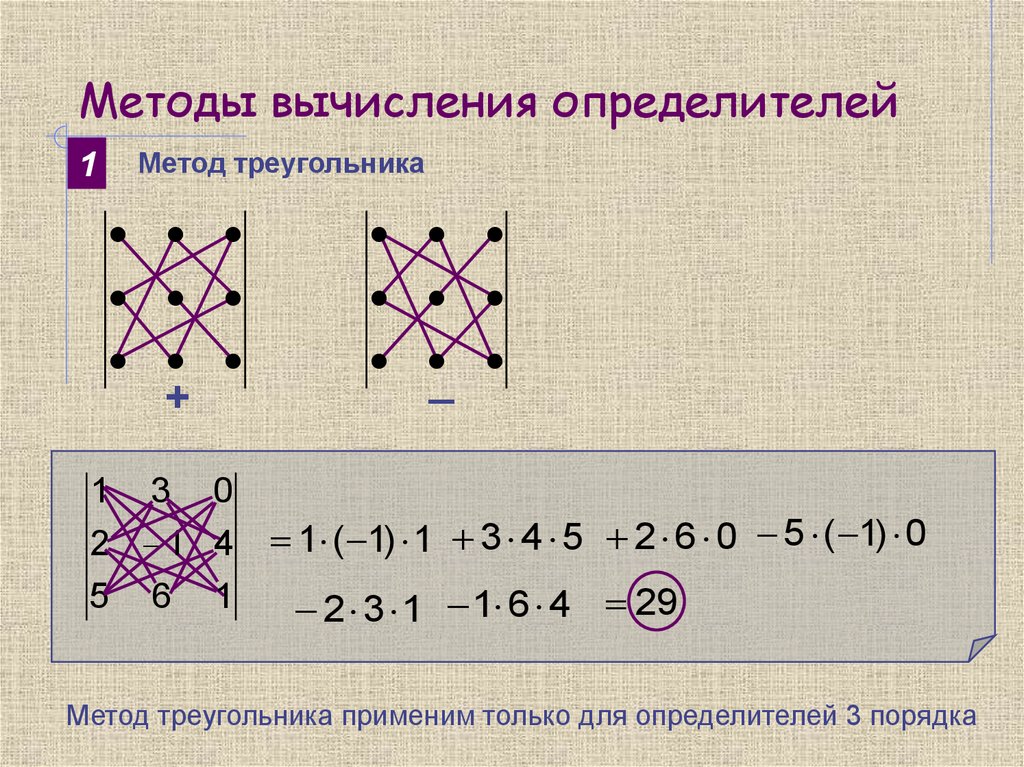
4. Методы вычисления определителей

1
Метод треугольника
+
1 3 0
2 1 4
5 6 1
_
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка

5. Методы вычисления определителей

2
Метод разложения определителя по элементам строки
(столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания i - й строки и j - го столбца, т.е.
строки и столбца, на пересечении которых стоит элемент ai j
называется минором элемента и обозначается Mi j
Алгебраическим дополнением элемента ai j называется
Ai j Mi j ( 1)i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
aa2211 aa2312
MM1123
aa3231 aa3332
1 1 2 3
A
M
(
M23
A11 23 M11 23( 1) 1) M
11

6. Методы вычисления определителей

Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
0 1
0 3
3 1
1 2
1 1
0 3 1 2
( 1) 0
( 1)1 3
( 1) 1
2 1
2 5
5 1
2 5 1
2 (3 1 5 1) 1 (0 1 2 1) 2

7. Методы вычисления определителей

3
Использование свойств определителя
Свойства определителя:
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
0 a22 0 a21 0
a21 a22
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
a11 a12 a11 a12 0

8. Методы вычисления определителей

меняет знак, если поменять местами строки (столбцы):
a11 a12
a21 a22
a11 a22 a12 a21 a12 a21 a11a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k a11 a22 k a12 a21 k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
a11 a12
a21 a22
a11 a21
a12 a22

9. Методы вычисления определителей

не меняется, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
a11
a12
a21 ka11 a22 ka12
a11a22 a21a12
a11a22 a11ka12 a21a12 ka11a12
a11 a12
a21 a22
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали: a a a
11
12
13
0 a22 a23 a11a22 a33
0 0 a33

10. Методы вычисления определителей

1 3 1
1
3 1 1 3 1
5 1
2 1 3 0 5 1 0 5 1 1
( 1)1 1
7 2
1 4 1
1 4 1 0 7 2
5 2 7 1 17
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.