Операции над множествами

1. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

2. Дополнение

Дополнением множества А
называется множество А, состоящее
из всех элементов универсального
множества, не принадлежащих
множеству А.
А={ x: x U x A }

3.

A
A
U
Для операции дополнения справедливы
следующие законы:
А А
– закон двойного отрицания
U; U
– закон обращения

4. Объединение

Объединением множеств А и В
называется множество А В,
состоящее из всех элементов,
принадлежащих хотя бы одному из
этих множеств.
А В={ x: x A x B }

5.

A
A B
B
Для операции объединения справедливы
следующие законы:
А А = А – закон идемпотентности
А В = В А – коммутативный закон
А ( В С) = ( А В ) С – ассоциативный
закон
А = А – закон нейтральности
А U = U – закон подавления

6. Пересечение

Пересечением множеств А и В
называется множество А В,
состоящее из всех общих элементов
этих множеств.
А В={ x: x A x B }

7.

A
A B
B
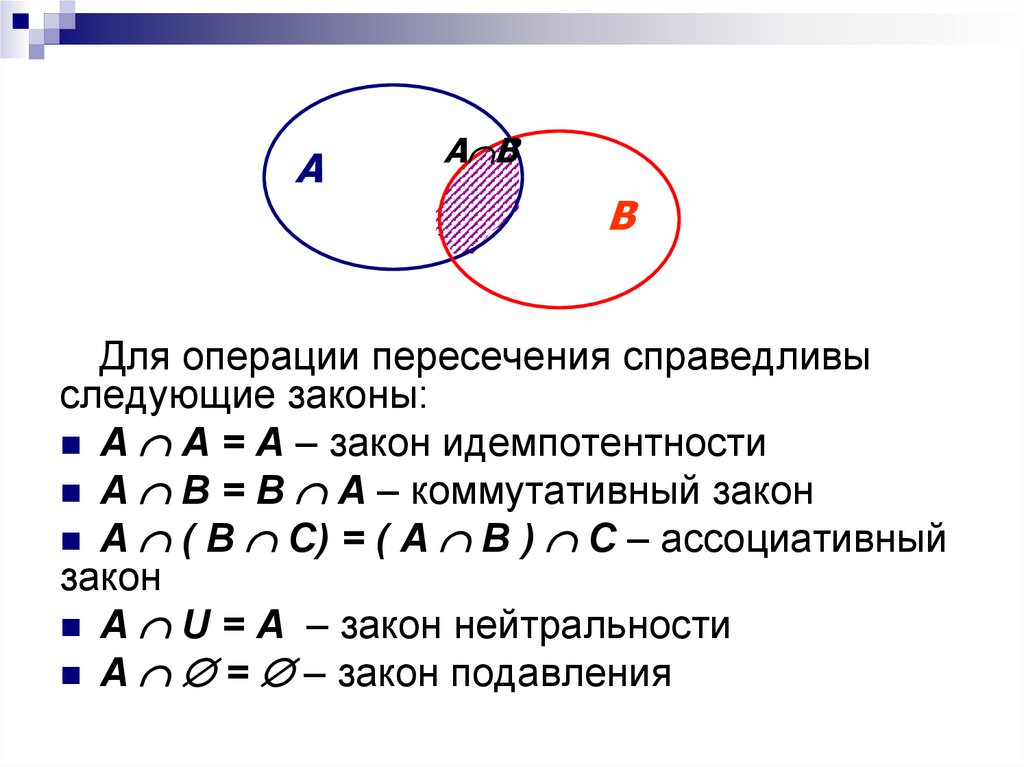
Для операции пересечения справедливы
следующие законы:
А А = А – закон идемпотентности
А В = В А – коммутативный закон
А ( В С) = ( А В ) С – ассоциативный
закон
А U = А – закон нейтральности
А = – закон подавления

8. Разность

Разностью множеств А и В
называется множество А\В,
состоящее из всех элементов
множества А, не принадлежащих В.
А\В ={ x: x A x B }

9.

А\В
A
B
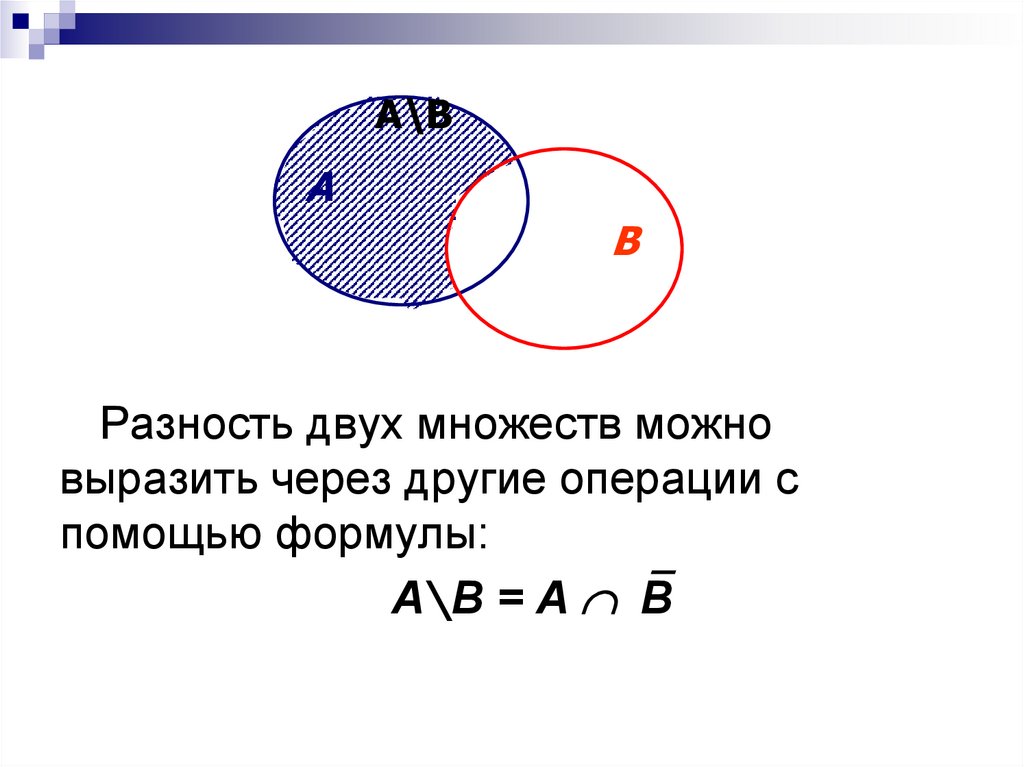
Разность двух множеств можно
выразить через другие операции с
помощью формулы:
А\В = А В

10. Симметрическая разность

Симметрической разностью
множеств А и В называется
множество А В, состоящее из
элементов, принадлежащих тому или
другому из этих множеств, но не
обоим сразу.
А В={ x: x A x B x A B }

11.

A
А В
B
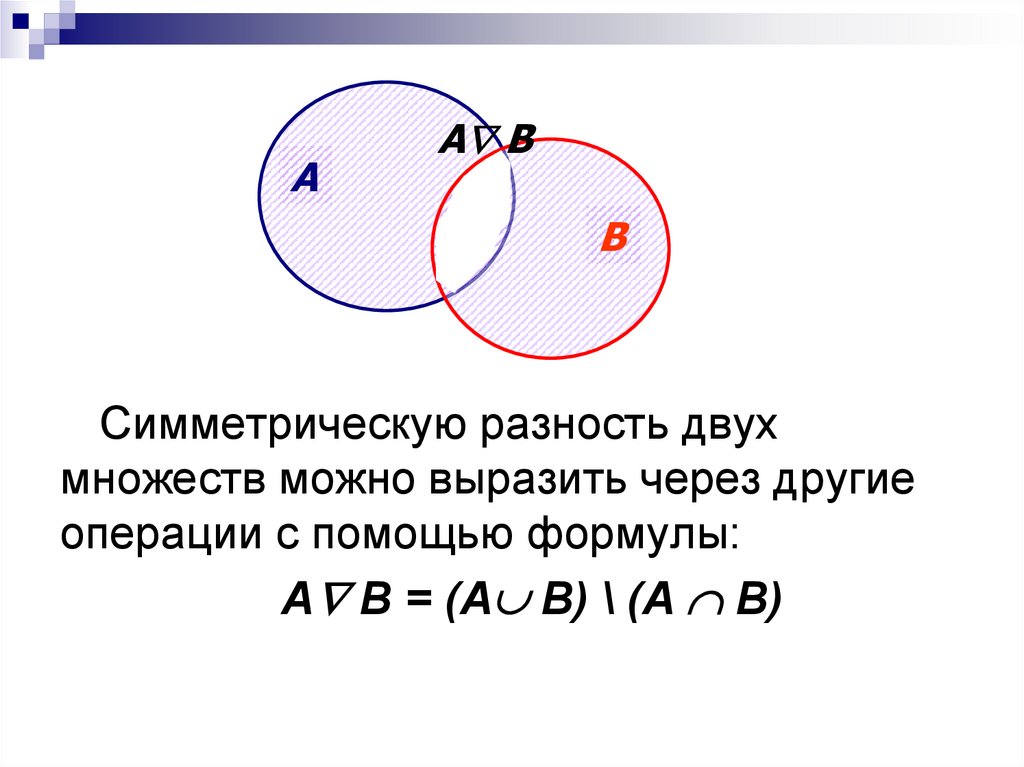
Симметрическую разность двух
множеств можно выразить через другие
операции с помощью формулы:
А В = (А В) \ (А В)

12. Примеры

А
В
АА ВВ
А\В
В\А
А В