Similar presentations:
Операции над множествами
1.
Пусть даны два множества А и В: А = {1,2,3}B = {3, 4, 5}
Объединение А В — это множество элементов,
принадлежащих или А, или В, или А и В вместе.
Пример: А В = {1, 2, 3, 4, 5}
2.
Пересечение А В – это множество элементов,принадлежащих одновременно А и В.
Пример: А В = {3}
Разность А \ В – это множество, состоящее из
элементов А, не принадлежащих В.
Пример: А \ В = {1,2}
B \ A = {4,5}
3.
Операции над множествами изображаются в виде круговЭйлера.
U
U
А
U
А
В
А В
U
А
В
А В
А
А\В
В
4.
UА
В
A B
U
В
А
A B
5.
Множество Ā = U \ A называется дополнениеммножества А до универсума U
U
Пусть А = {1,2,3}
А
U = {1, 2, 3, 4, 5}
Ā = U \ A = {4, 5,}
6.
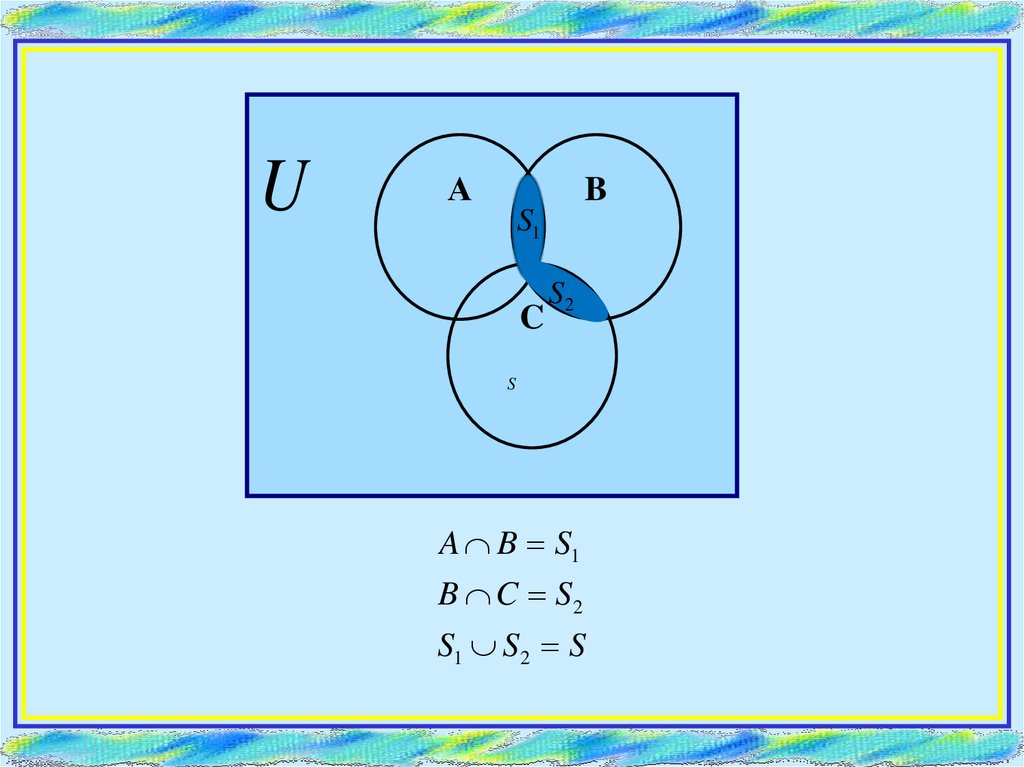
UА
B
S1
C
S2
S
A B S1
B C S2
S1 S2 S
7.
UА
B
C
S A\ B \ C
8.
BA
S1
S2
C
S1 A \ B \ C
S2 ( B C ) \ A
S S1 S2
U
9.
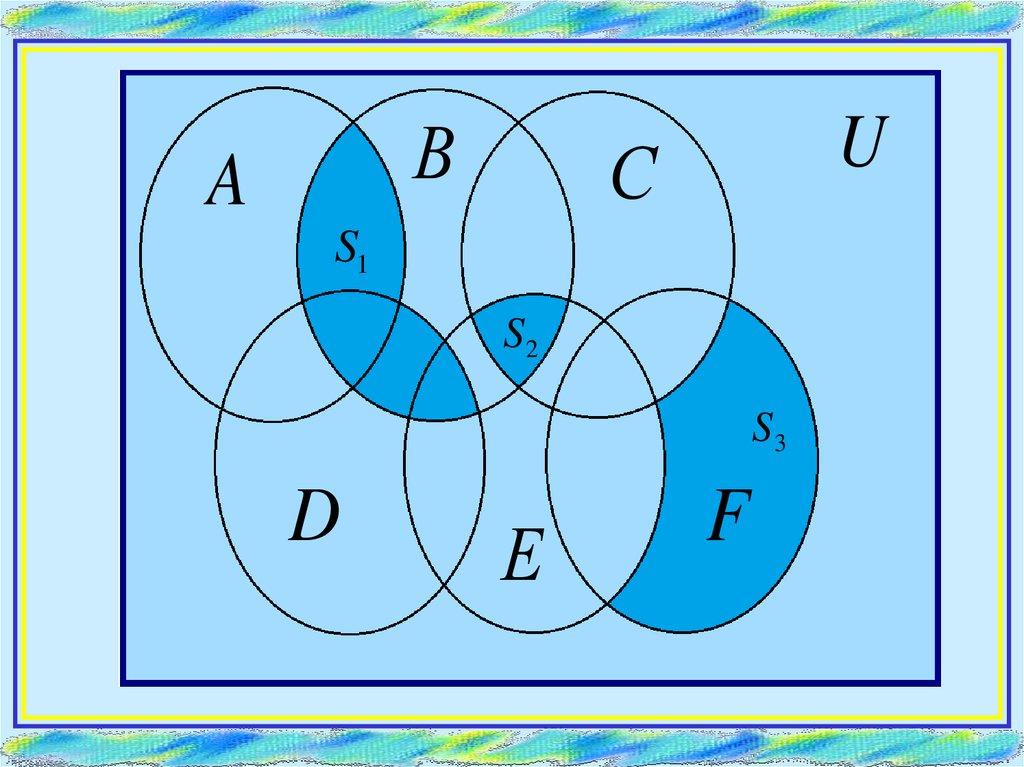
Пусть элементами множеств являются точкикругов A, B, C, D, E, F, а универсумом U — точки
прямоугольника. С помощью теоретико-множественных
операций описать элементы множеств,
принадлежащие заштрихованным областям S1, S2, S3
и общей заштрихованной области S.
10.
ВA
U
С
S1
S2
S3
D
Е
F
11.
S1 = (A B) (B D)S2 = B C E
S3 = F \ C \E
S = S1 S2 S3
12.
Отобразить множество:A (B C)
13.
СВ
U
B C
С
В
А
А (B C)
U
14.
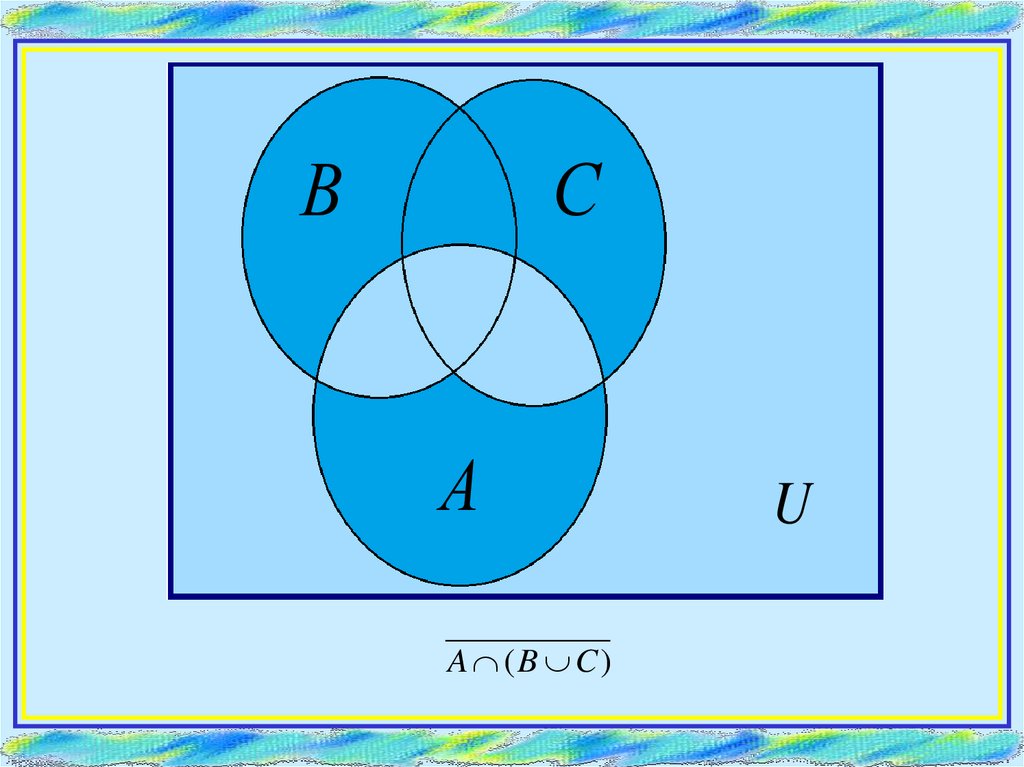
СВ
А
A (B C)
U
15.
Пусть U — универсальное множество,A, B, C — произвольные множества.
Тогда справедливы следующие свойства:
1. Идемпотентность:
2. Коммутативность:
A A=A A A=A
A B = B A
A B = B A
16.
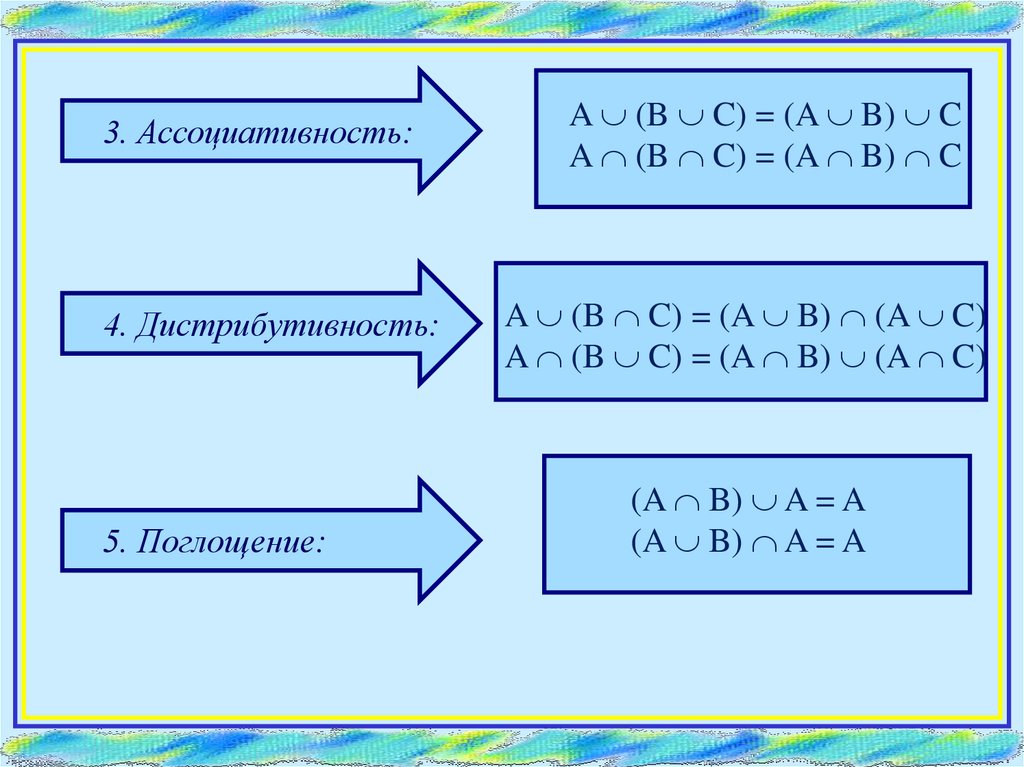
3. Ассоциативность:4. Дистрибутивность:
5. Поглощение:
A (B C) = (A B) C
A (B C) = (A B) C
A (B C) = (A B) (A C)
A (B C) = (A B) (A C)
(A B) A = A
(A B) A = A
17.
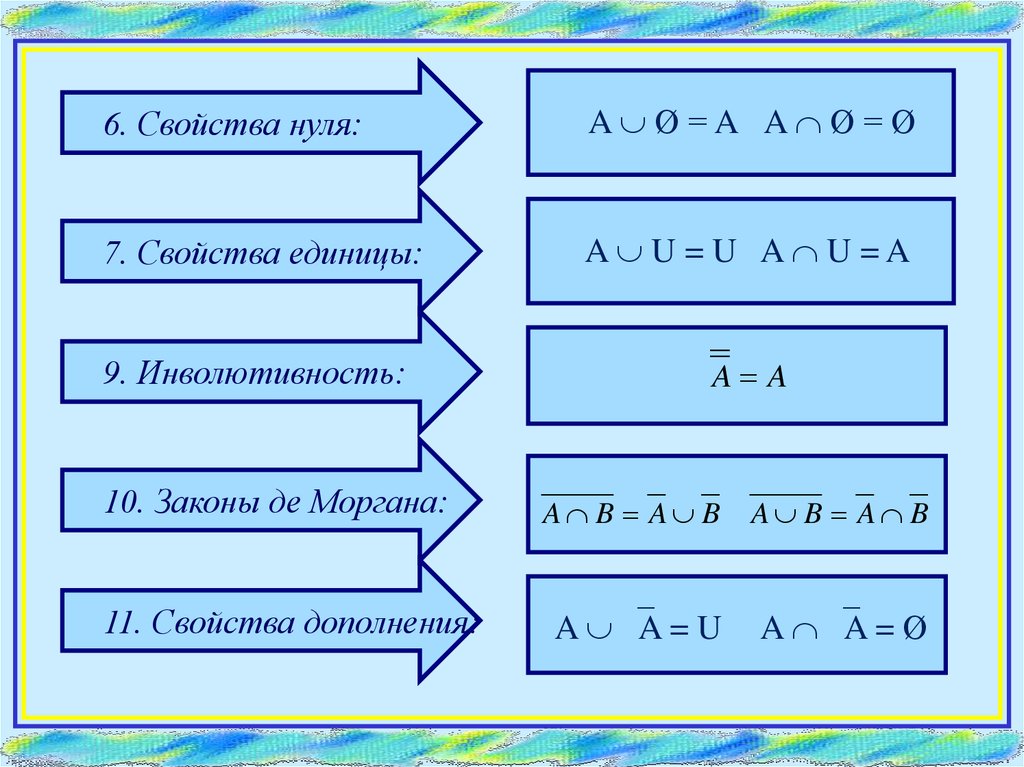
6. Свойства нуля:A Ø=A A Ø=Ø
7. Свойства единицы:
A U =U A U =A
9. Инволютивность:
A A
10. Законы де Моргана:
11. Свойства дополнения:
A B A B
A B A B
A A = U
A A = Ø












 mathematics
mathematics








