Similar presentations:
Неопределенный и определенный интегралы
1.
Неопределенный и определенный интегралы, ихсвойства. Несобственные интегралы с
бесконечными пределами интегрирования
Повторение материала 1-го курса
1) Первообразная
2.
ПервообразнаяФункция F(x) называется
первообразной для функции f(x) на
данном промежутке, если для любого x
из этого промежутка F’(x) = f(x).
3.
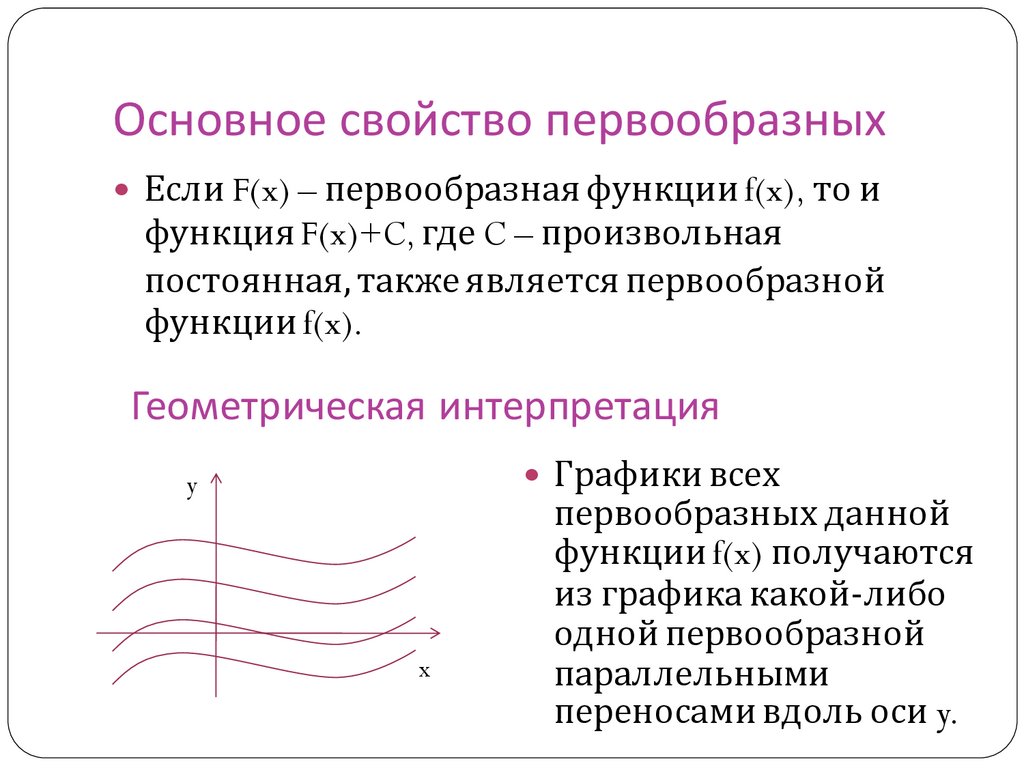
Основное свойство первообразныхЕсли F(x) – первообразная функции f(x), то и
функция F(x)+C, где C – произвольная
постоянная, также является первообразной
функции f(x).
Геометрическая интерпретация
Графики всех
y
x
первообразных данной
функции f(x) получаются
из графика какой-либо
одной первообразной
параллельными
переносами вдоль оси y.
4.
5.
6.
2) Неопределенный интегралСовокупность всех первообразных данной
функции f(x) называется ее неопределенным
интегралом и обозначается f ( x)dx :
f ( x)dx = F ( x) + C ,
где C – произвольная постоянная.
7.
Таблица неопределённых интегралов8.
Правила интегрированияcf ( x)dx = c f ( x)dx, c = const
( f ( x) g ( x))dx = f ( x)dx g ( x)dx
1
f (ax + b)dx = a F (ax + b) + C , a 0
9.
10.
11.
12.
3) Определенный интегралВ декартовой прямоугольной
системе координат XOY фигура,
ограниченная осью OX, прямыми
x=a, x=b (a<b) и графиком
непрерывной неотрицательной
на отрезке [a;b] функции y=f(x),
называется криволинейной
трапецией
13.
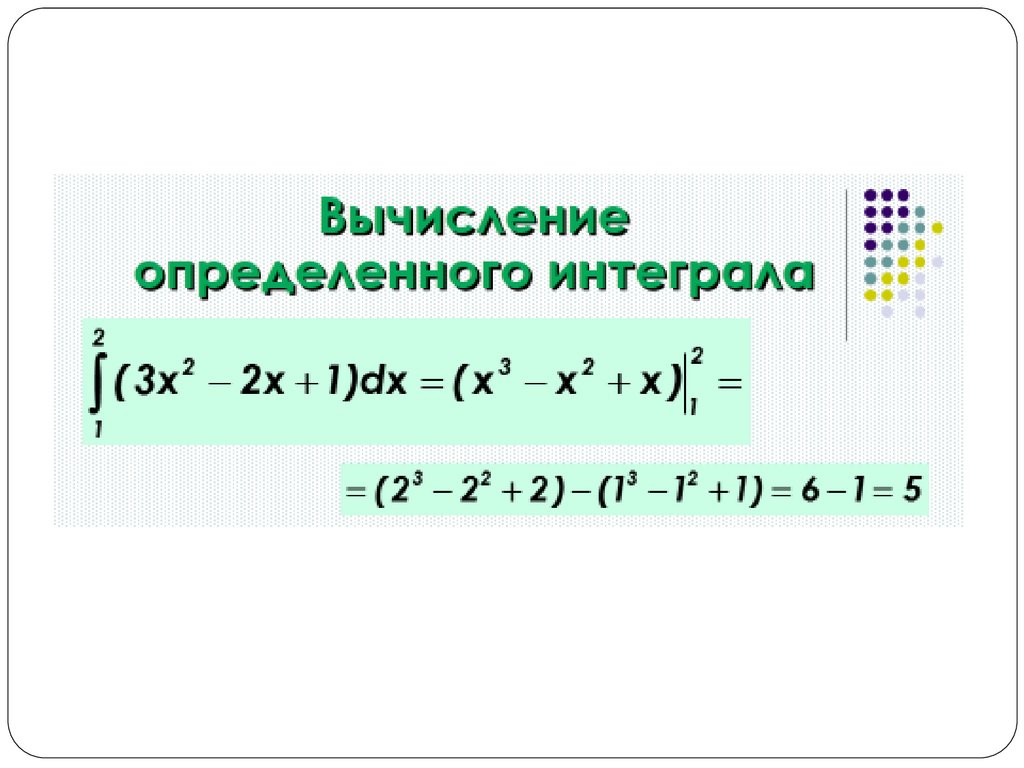
Связь между определенныминтегралом и первообразной
(Формула Ньютона - Лейбница)
Для непрерывной функции
b
f
(
x
)
dx
=
F
(
x
)
|
=
F
(
b
)
−
F
(
a
)
b
a
a
где F(x) – первообразная функции f(x).
14.
Основные свойства определенногоинтеграла
a
f
(
x
)
dx
=
0
a
b
dx = b − a
a
b
a
a
b
f
(
x
)
dx
=
−
f
(
x
)
dx
15.
Основные свойства определенногоинтеграла
b
c
b
a
a
c
f
(
x
)
dx
=
f
(
x
)
dx
+
f
(
x
)
dx
b
b
a
a
cf ( x)dx = c f ( x)dx, c − const
b
b
b
a
a
a
(
f
(
x
)
g
(
x
))
dx
=
f
(
x
)
dx
g
(
x
)
dx
16.
17.
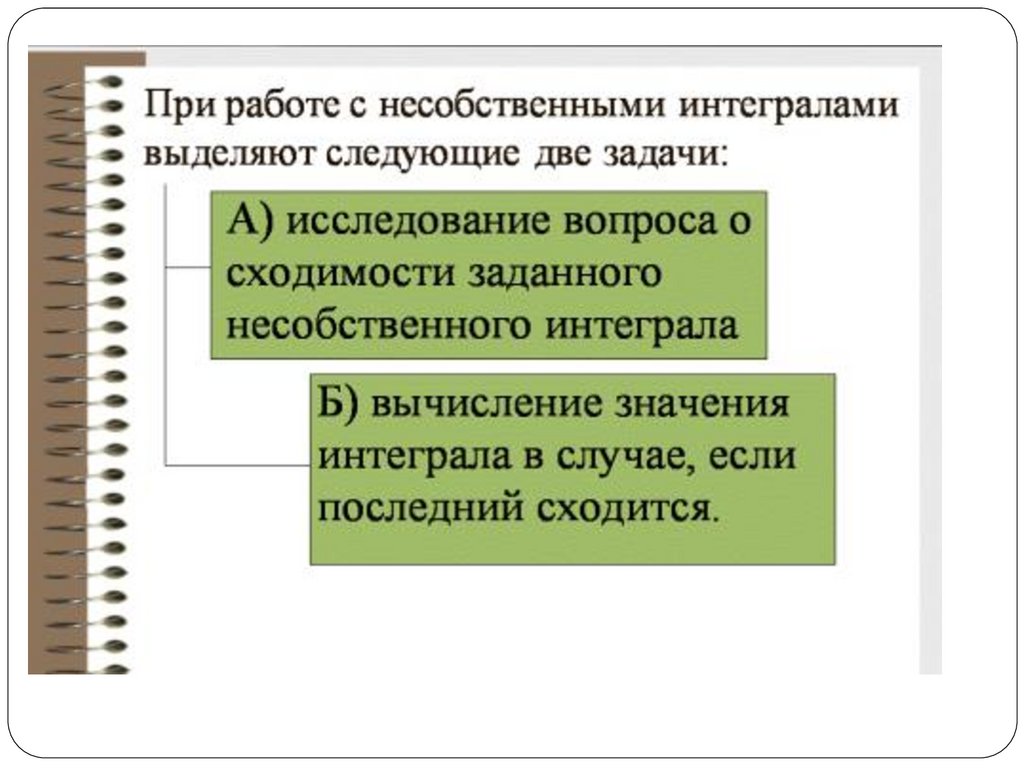
Несобственные интегралы сбесконечными пределами
интегрирования
18.
19.
20.
21.
Пример:1
1
Для х2 первообразной является х
1
стремится к нулю, т.к. 1 разделить на очень большое число получится



















 mathematics
mathematics








