Определенные и неопределенные интегралы

1.

Тема: «Определенные и
неопределенные
интегралы»
Выполнил:
Кудря Сергей.

2.

• Интегральное исчисление появилось
во времена античного периода
развития математической науки и
началось с метода исчерпывания,
который р азработан математиками
Древней Греции, и представлял собой
набор правил, разработанных
Евдоксом Книдским . По этим
правилам вычисляли площади и
объёмы.

3.

• Цель: изучить актуальности применения определенного и
неопределенного интеграла , а также широты их использования не
только в математике, но и других науках, оценить ее практическую и
теоретическую значимость.
• Задачи:
• 1) Найти информацию о определенном интеграле, изучить ее;
• 2) Найти информацию о неопределенном интеграле, изучить ее;
• 3)Обобщить собранный материал.

4.

• Курс
математического анализа содержит разнообразный материал,
однако, одним из его центральных разделов являются определенный и
неопределенный интегралы. Интегрирование многих видов функций
подчас
представляет
собой
одну
из
труднейших
проблем
математического анализа.

5.

Определенный интеграл.

6.

Для вычисления определенного
интеграла нужно:
• 1) Найти какую-нибудь первообразованую для
функции ( найти неопределенный интеграл от
функции, в котором можно принять С=0 ) ;
• 2) В полученном выражении подставить вместо
х сначала верхний предел, а затем нижний
предел, и из результата первой подстановки
вычесть результат второй.

7.

Замена переменной в определённом
интеграле :
• Он заключается в преобразовании определённого интеграла с
помощью подстановки t=w(x) или x=g(t) в определённый интеграл
относительно новой переменной t. При этом старые пределы
интегрирования a и b заменяются соответственно новыми
пределами интегрирования c и d, которые находятся из исходной
подстановки.

8.

9.

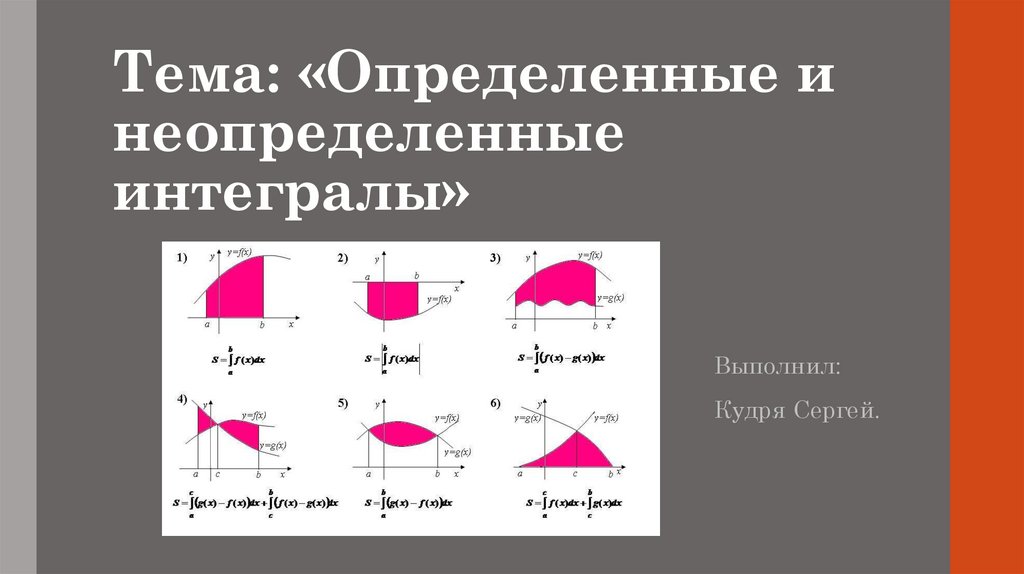
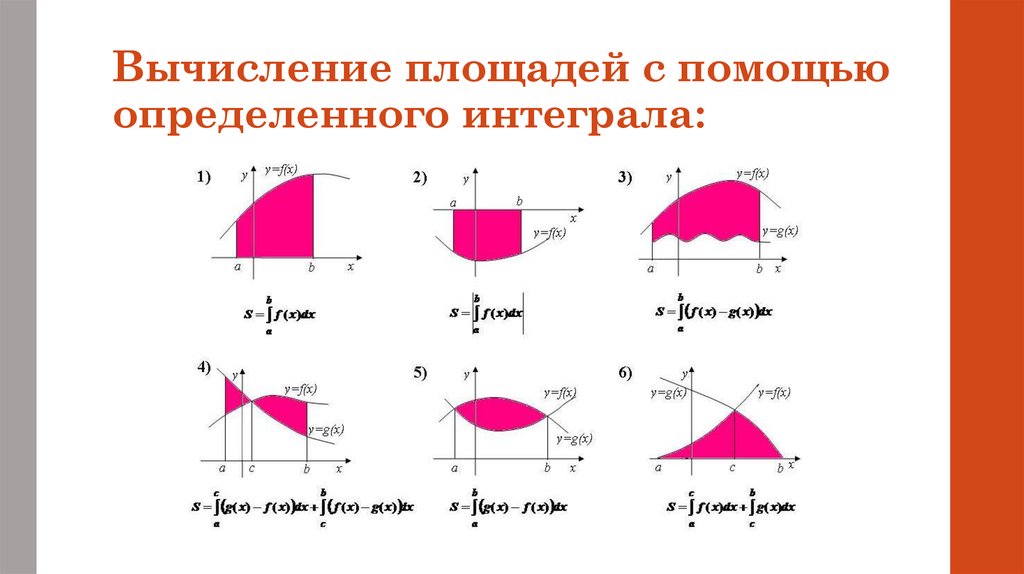
Вычисление площадей с помощью
определенного интеграла:

10.

Неопределенный интеграл:
• Неопределенным интегралом некой функции f(x)
называют совокупность всех первообразных
рассматриваемой функции.

11.

12.

13.

14.

Заключение:
• Трудно назвать научную область, в которой бы не применялись методы
интегрального исчисления, в общем, и свойства определенного и
неопределенного интеграла, в частности. Так в процессе выполнения
проектной работы мной были рассмотрены примеры практических задач
в области геометрии. Также определенный и неопределенный интегралы
используется для изучения собственно самой математики. Например,
при решении дифференциальных уравнений, которые в свою очередь
вносят свой незаменимый вклад в решение задач практического
содержания. Можно сказать, что определенный и неопределенный
интегралы – это некоторый фундамент для изучения математики. Отсюда
и важность знания методов их решения.

15.

Источники информации:
https://ru.wikipedia.org/wiki
https://tutoronline.ru/
https://multiurok.ru/blog/poluchite-novye-svidetelstva-opublikatsii.html?utm_source=multiurok&utm_medium=banner&utm_
campaign=mheadtop&utm_content=multiurokblog&utm_term=20200
616newsvid
https://infourok.ru/
https://videouroki.net/course/?utm_source=multiurok&utm_medium=b
anner&utm_campaign=mheadtop&utm_content=course&utm_term=2
0240208courses