Операции компьютерной графики

1.

Лекция 1
перации компьютерной гра
ики
Системное изложение универсального подхода
Олег Игоревич Мухин
Курс для инженеров - системотехников
Компьютерная графика
Автор:

2.

Литература (лучшее)
• Роджерс Д., Адамс Дж. Математические основы машинной графики. /под ред. Ю.М. Баяковского,
В.А. Галактионова, В.В. Мартынюка. — М.: Мир, 2001. — 604 с.: ил. — ISBN 5-03-002143-4. - Режим
доступа: https://mymirknig.ru/knigi/design_grafika/17926-matematicheskie-osnovy-mashinnoygrafiki.html (толстое и понятное изложение на 50 лет вперед)
• Роджерс Д.Ф. Алгоритмические основы машинной графики. Учебное издание /под ред. Ю.М.
Баяковского, В.А. Галактионова, В.В. Мартынюка. — М.: Мир, 1989. - Режим доступа:
https://www.studmed.ru/rodzhers-d-algoritmicheskie-osnovy-mashinnoy-grafiki_99ccb2eefa7.html (для
программистов на 10 лет вперед)
• Ф. Клейн «Элементарная математика с точки зрения высшей. Т.2. Геометрия»: -М., Наука, 1987.
(умное, абстрактное, сложное обобщение на века)
• Аммерал (4 небольших книги с кодами для программистов,1992): Интерактивная трехмерная
графика, Принципы программирования в машинной графике, Программирование графики на
турбо СИ, Машинная графика на ПК.
• Сайт stratum.ac.ru – вход для студентов – Учебник «Компьютерная графика» http://www.stratum.ac.ru/education/textbooks/kgrafic/contents.html Код доступа: kglection
• Видео лекций и семинаров на https://bigbluebutton.pstu.ru/b/oim-crw-zkr-xre и
https://bigbluebutton.pstu.ru/b/oim-qyo-d32-0tu

3.

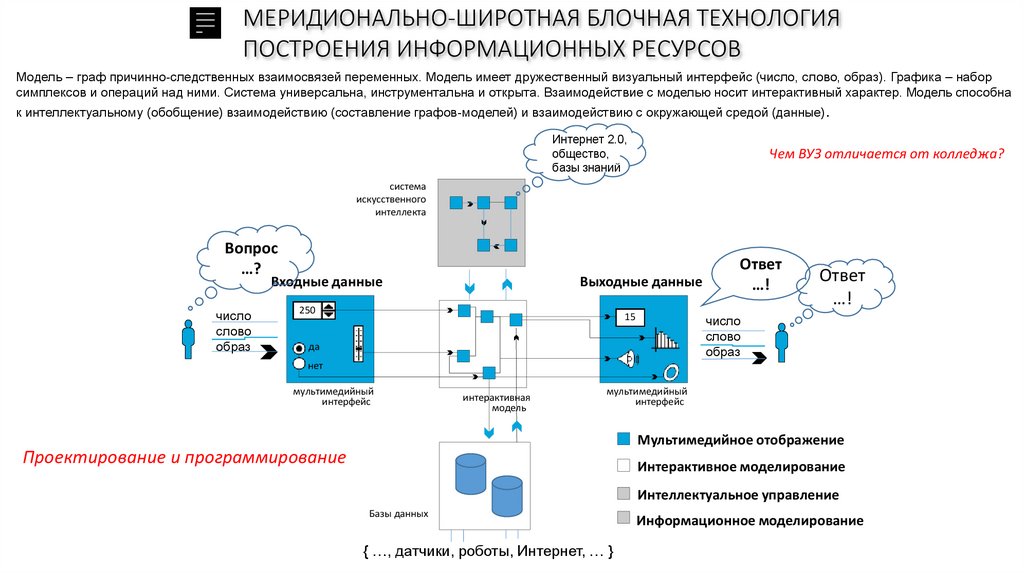
МЕРИДИОНАЛЬНО-ШИРОТНАЯ БЛОЧНАЯ ТЕХНОЛОГИЯ
ПОСТРОЕНИЯ ИНФОРМАЦИОННЫХ РЕСУРСОВ
Модель – граф причинно-следственных взаимосвязей переменных. Модель имеет дружественный визуальный интерфейс (число, слово, образ). Графика – набор
симплексов и операций над ними. Система универсальна, инструментальна и открыта. Взаимодействие с моделью носит интерактивный характер. Модель способна
к интеллектуальному (обобщение) взаимодействию (составление графов-моделей) и взаимодействию с окружающей средой (данные).
Интернет 2.0,
общество,
базы знаний
Чем ВУЗ отличается от колледжа?
система
искусственного
интеллекта
Вопрос
…?
Входные данные
число
слово
образ
Выходные данные
250
15
Ответ
…!
Ответ
…!
число
слово
образ
да
нет
мультимедийный
интерфейс
интерактивная
модель
мультимедийный
интерфейс
Мультимедийное отображение
Проектирование и программирование
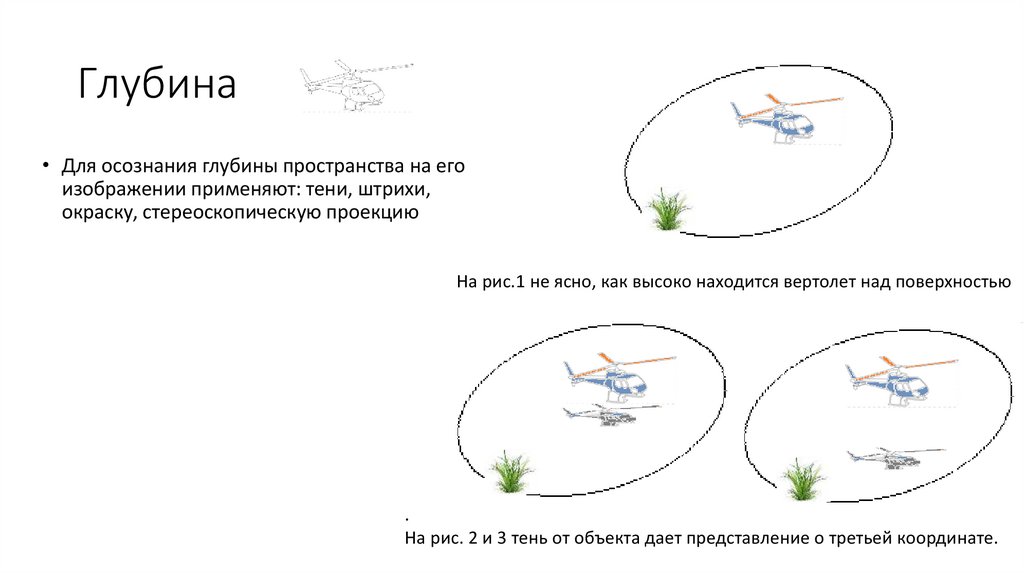
Интерактивное моделирование
Интеллектуальное управление
Базы данных
{ …, датчики, роботы, Интернет, … }
Информационное моделирование

4.

Задача компьютерной графики
Сцена – множество (106) сложных графических объектов, подвергаемых
пространственным преобразованиям со скоростью 1/100 Гц с целью обеспечения
реалистичности и точности
Внимание! Не алгоритмы!
Сложное – множество, состоящее из простых элементов (simple), связанных
базовыми операциями (basic) и отношениями между собой.
Задача:
• разбить сложное на простое,
• определить операции с простыми объектами,
• сгруппировать простое в сложное.
Пожелания, требования: универсально, единообразно, быстро, просто, надежно.

5.

Роль КГ
• Современное ПО без графического интерфейса?
• Геометрия пространства – основа организации мира
• Понимать – это представлять себе, рисовать в своем воображении
• КГ - основа ИИ
• Что такое число (отрицательное, мнимое, дробное, бесконечность)?
• Многомерность
• Фрактальность
• Реалистичность
• Виртуальность
• Добро, истина и красота– критерии работы инженера
(добро – это слово, истина – это число, красота – это образ)

6.

• «Геометрия – математическая наука, так как ее выводы чисто
логические, но и физическая наука, так как аксиомы относятся к
физической реальности»
Альберт Эйнштейн

7.

Вспомним школу
Декартовы координаты
1. Точка в 2D-пространстве представлена двумя
числами (координатами): Q(x, y). Структура данных –
множество «ключевых» точек.
2. Операция над графическим
объектом (ГО) представлена матрицей:
(четыре числа)
a
b
c
d
3. Результат операции над точкой xисх yисх – точка в новом положении
с координатами (xнов, yнов)
X
Y
xисх yисх
a
b
Следствие: S’ = S*det( c
d
a
* c
b
d
) = S*(ad - bc)
=
ax+cy
bx+dy
xнов yнов
Сущность – вектор.
Действие – матрица.
Признак – скаляр.
Свойство – число.
(S – площадь фигуры)

8.

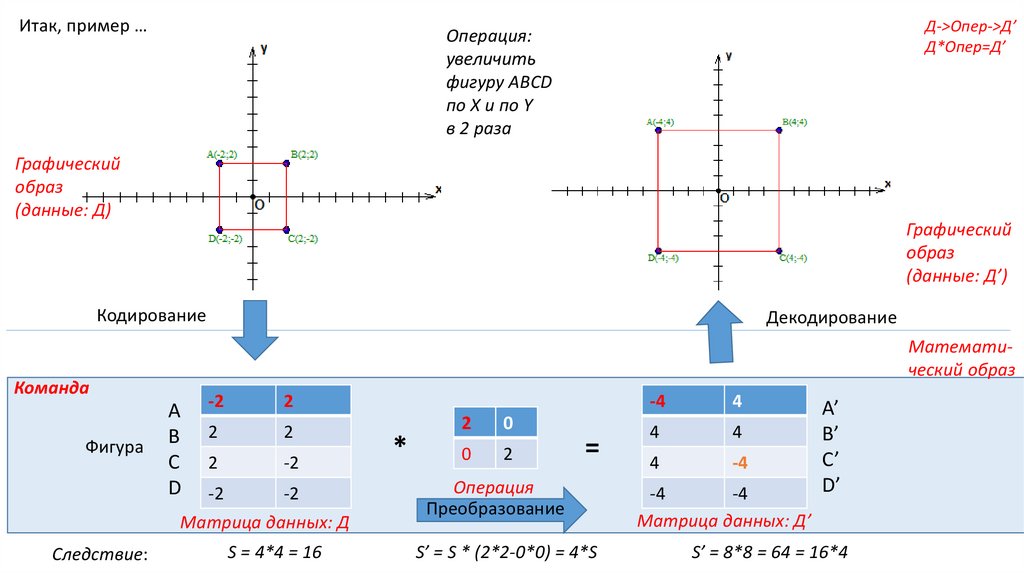
Итак, пример …
Д->Опер->Д’
Д*Опер=Д’
Операция:
увеличить
фигуру ABCD
по Х и по Y
в 2 раза
Графический
образ
(данные: Д)
Графический
образ
(данные: Д’)
Кодирование
Математический образ
Команда
Фигура
Следствие:
Декодирование
A
B
C
D
-2
2
2
2
2
-2
*
2
0
0
2
=
-2
-2
Матрица данных: Д
Операция
Преобразование
S = 4*4 = 16
S’ = S * (2*2-0*0) = 4*S
-4
4
4
4
4
-4
-4
-4
Матрица данных: Д’
A’
B’
C’
D’
S’ = 8*8 = 64 = 16*4

9.

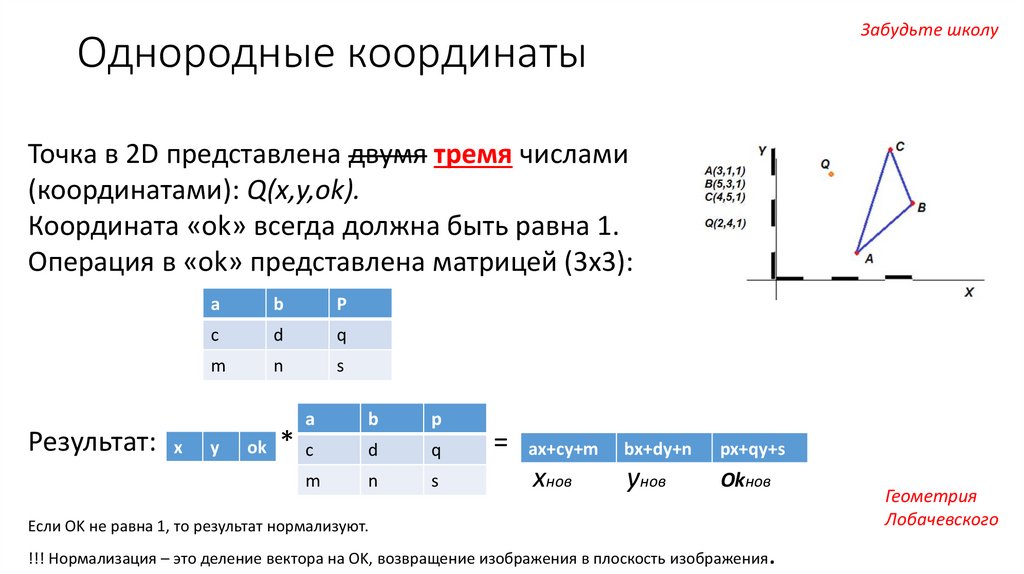
Забудьте школу
Однородные координаты
Точка в 2D представлена двумя тремя числами
(координатами): Q(x,y,ok).
Координата «оk» всегда должна быть равна 1.
Операция в «ok» представлена матрицей (3х3):
Результат: x
a
b
P
c
d
q
m
n
s
a
y
ok * c
m
b
p
d
q
n
= = ax+cy+m bx+dy+n
xнов
yнов
s
px+qy+s
Okнов
Если OK не равна 1, то результат нормализуют.
!!! Нормализация – это деление вектора на OK, возвращение изображения в плоскость изображения
.
Геометрия
Лобачевского

10.

Об основах договариваются. Стандарт!
0, 1, вращение правого винта i, вектор-иерархия
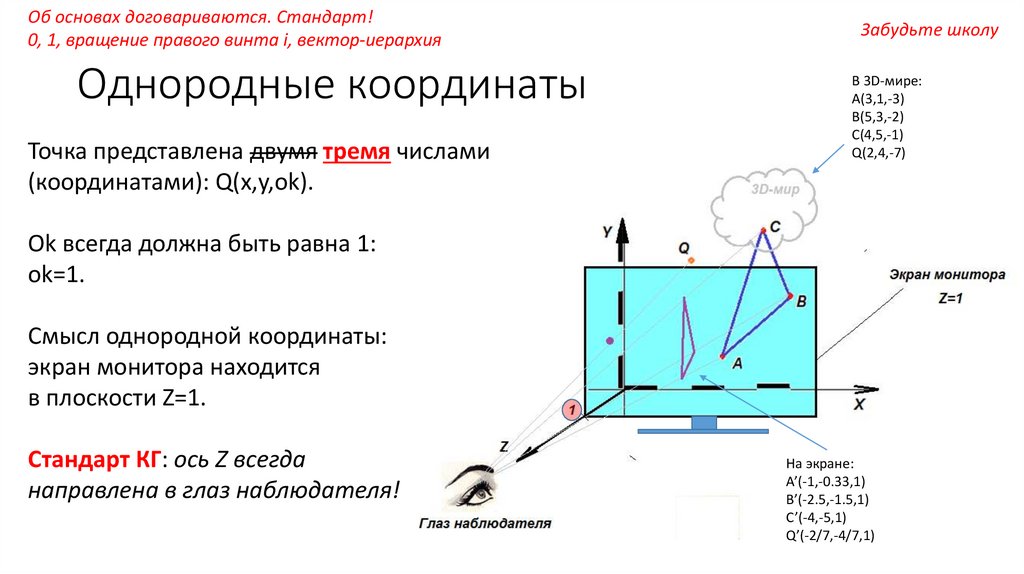
Однородные координаты
Точка представлена двумя тремя числами
(координатами): Q(x,y,ok).
Забудьте школу
В 3D-мире:
A(3,1,-3)
B(5,3,-2)
C(4,5,-1)
Q(2,4,-7)
Ok всегда должна быть равна 1:
ok=1.
Смысл однородной координаты:
экран монитора находится
в плоскости Z=1.
Стандарт КГ: ось Z всегда
направлена в глаз наблюдателя!
На экране:
A’(-1,-0.33,1)
B’(-2.5,-1.5,1)
C’(-4,-5,1)
Q’(-2/7,-4/7,1)

11.

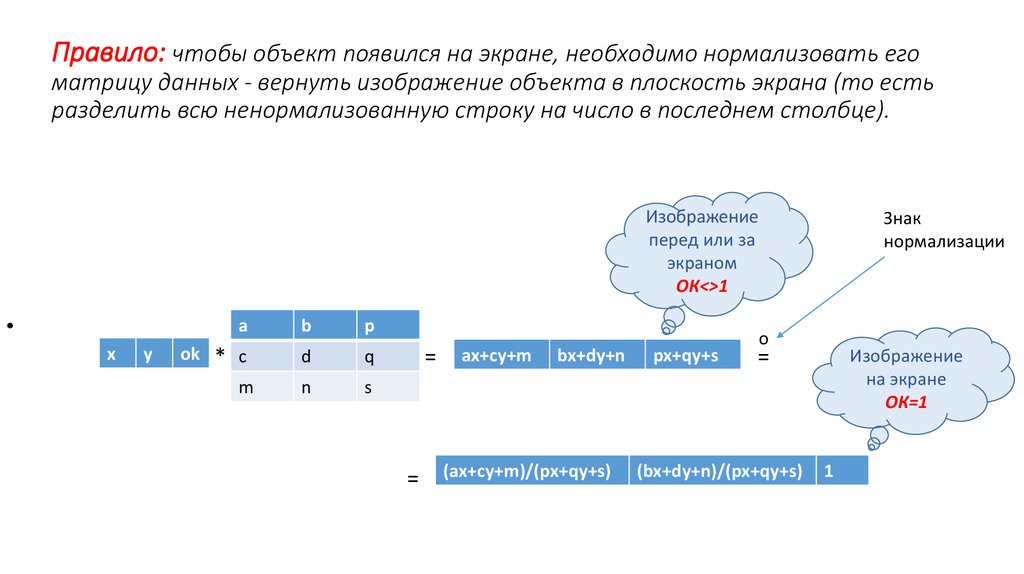
Правило: чтобы объект появился на экране, необходимо нормализовать его
матрицу данных - вернуть изображение объекта в плоскость экрана (то есть
разделить всю ненормализованную строку на число в последнем столбце).
Изображение
перед или за
экраном
ОК<>1
x
y
ok
a
b
p
* c
d
q
m
n
s
=
=
ax+cy+m
bx+dy+n
(ax+cy+m)/(px+qy+s)
px+qy+s
Знак
нормализации
o
=
(bx+dy+n)/(px+qy+s)
Изображение
на экране
ОК=1
1

12.

Причины введения однородных координат
• Введение перспективы в изображение
a b p
c d q
• Доступность ВСЕХ базовых операций на единой основе
m n s
• Возможность работы с бесконечными объектами
• Работа в матричной алгебре универсальным способом (полнота базовых
действий на единой основе)
• Ускорение расчетов за счет введения и использования матричных процессоров
(видеокарт, графических ускорителей), увеличение размерности шины
• Расширение математической модели графики
• Доступ к рациональным отношениям
• Переход к комплексным преобразованиям
• Исключение опасных операций и разветвлений

13.

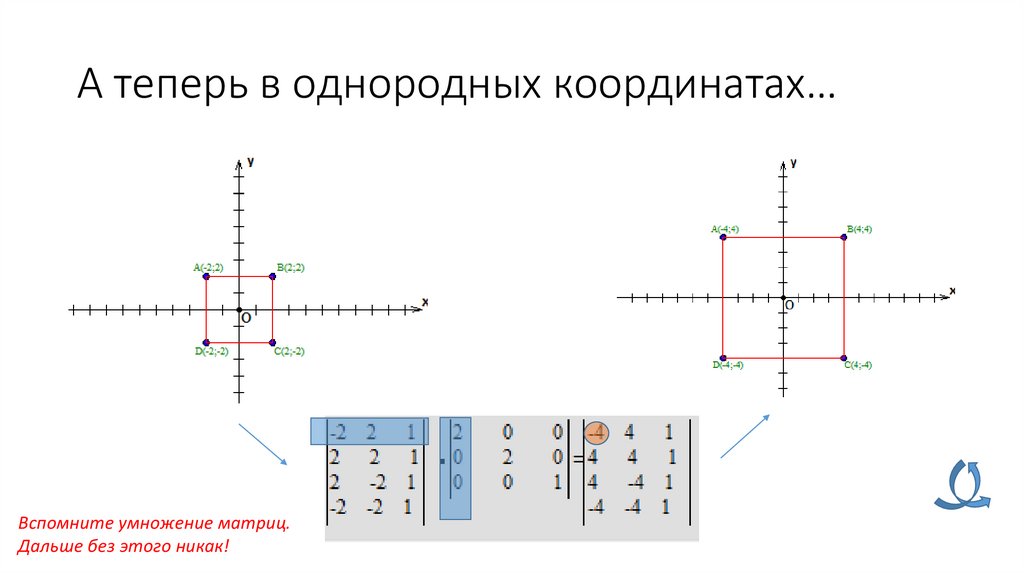
А теперь в однородных координатах…
Вспомните умножение матриц.
Дальше без этого никак!

14.

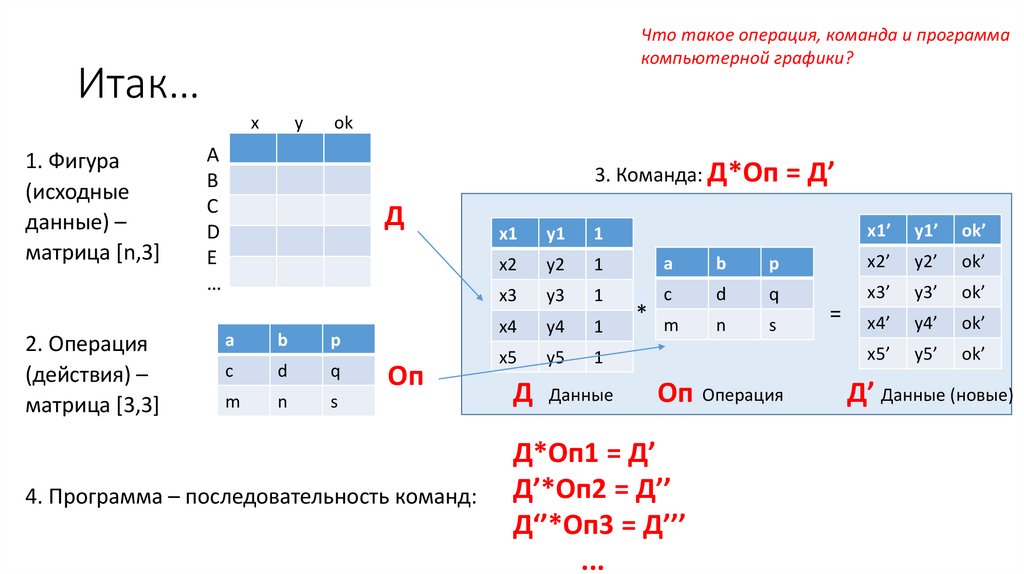
Что такое операция, команда и программа
компьютерной графики?
Итак…
x
1. Фигура
(исходные
данные) –
матрица [n,3]
2. Операция
(действия) –
матрица [3,3]
y
ok
A
B
C
D
E
…
3. Команда: Д*Оп = Д’
Д
a
b
p
c
d
q
m
n
s
Оп
4. Программа – последовательность команд:
x1’
y1’
ok’
p
x2’
y2’
ok’
d
q
x3’
y3’
ok’
n
s
x4’
y4’
ok’
x5’
y5’
ok’
x1
y1
1
x2
y2
1
a
b
x3
y3
1
c
x4
y4
1
x5
y5
1
Д Данные
* m
Оп Операция
Д*Оп1 = Д’
Д’*Оп2 = Д’’
Д‘’*Оп3 = Д’’’
...
=
Д’ Данные (новые)

15.

Пять базовых операций – полная система
операций компьютерной графики: «T,R,S,M,P»
• Смещение (transfer, T)
• Вращение (rotation, R)
• Масштабирование (scaling, S)
• Зеркалирование (mirroring, M)
• Проецирование (projection, P)
!
Чтобы получить новое положение графического объекта, достаточно умножить координаты всех его вершин на
матрицу преобразования. Если преобразование сложное, то умножать исходный объект надо
последовательно на каждую из базовых матриц. Потом вершины соединить прямыми линиями как на
исходной фигуре.

16.

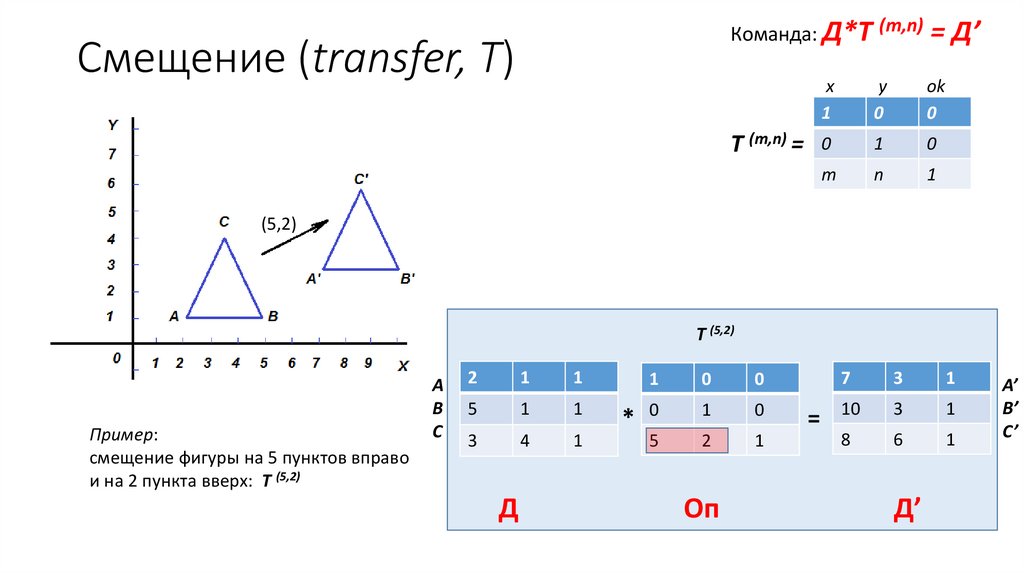
Команда: Д*T (m,n) = Д’
Смещение (transfer, T)
x
1
y
0
ok
0
T (m,n) = 0
1
0
m
n
1
(5,2)
Т (5,2)
Пример:
смещение фигуры на 5 пунктов вправо
и на 2 пункта вверх: Т (5,2)
A
B
C
2
1
1
1
0
0
5
1
1
1
0
3
4
1
* 0
2
1
Д
5
Оп
=
7
3
1
10
3
1
8
6
1
Д’
A’
B’
C’

17.

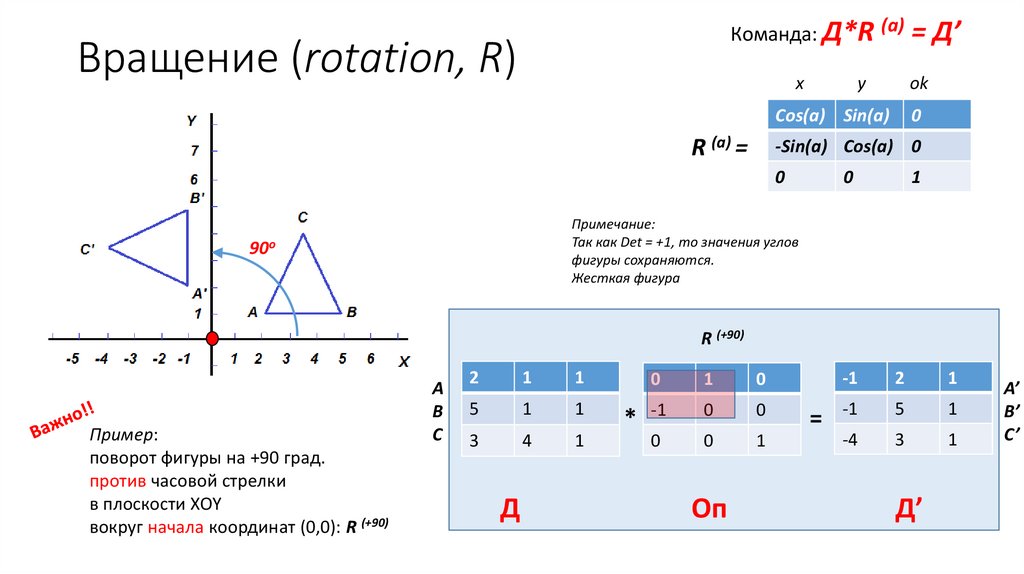
Команда: Д*R (a) = Д’
Вращение (rotation, R)
x
y
ok
Cos(a) Sin(a)
R (a) =
0
-Sin(a) Cos(a) 0
0
0
1
Примечание:
Так как Det = +1, то значения углов
фигуры сохраняются.
Жесткая фигура
90o
R (+90)
Пример:
поворот фигуры на +90 град.
против часовой стрелки
в плоскости XOY
вокруг начала координат (0,0): R (+90)
A
B
C
2
1
1
0
1
0
5
1
1
0
0
3
4
1
* -1
0
1
Д
0
Оп
=
-1
2
1
-1
5
1
-4
3
1
Д’
A’
B’
C’

18.

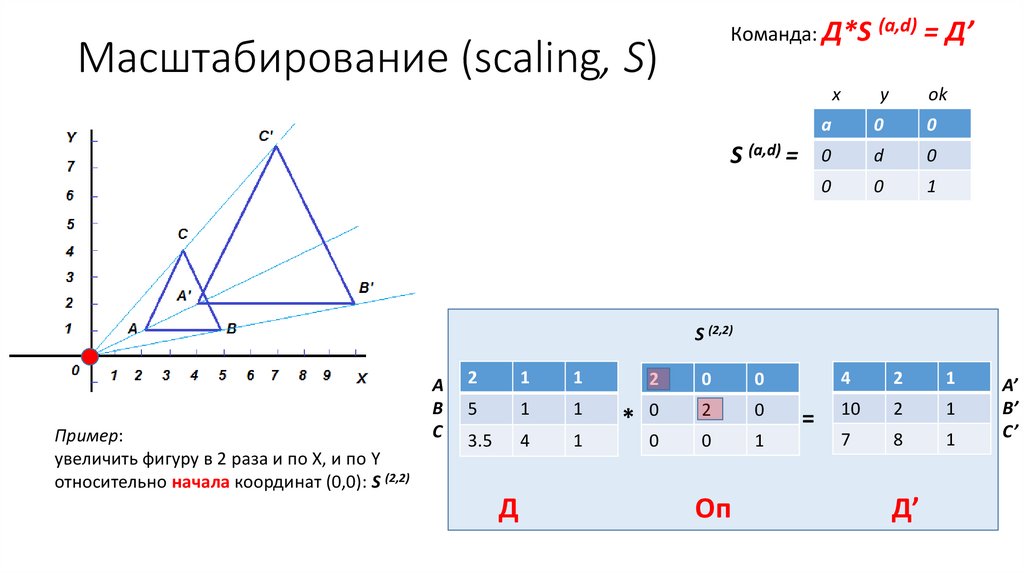
Команда: Д*S (a,d) = Д’
Масштабирование (scaling, S)
x
S (a,d) =
y
ok
a
0
0
0
d
0
0
0
1
S (2,2)
Пример:
увеличить фигуру в 2 раза и по Х, и по Y
относительно начала координат (0,0): S (2,2)
A
B
C
2
1
1
2
0
0
5
1
1
2
0
3.5
4
1
* 0
0
1
Д
0
Оп
=
4
2
1
10
2
1
7
8
1
Д’
A’
B’
C’

19.

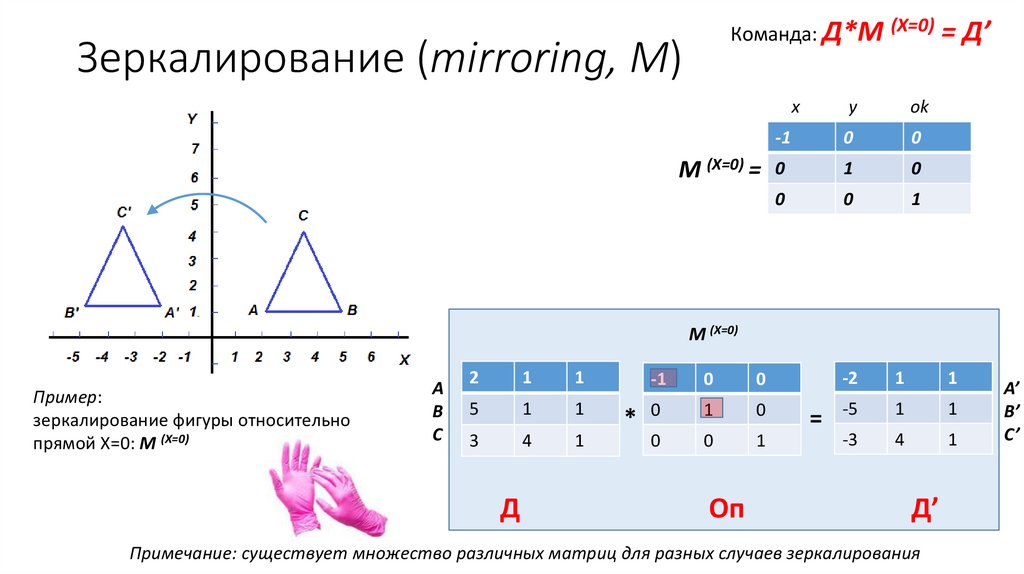
Команда: Д*M (X=0) = Д’
Зеркалирование (mirroring, M)
x
y
ok
-1
0
0
M (X=0) = 0
1
0
0
0
1
M (X=0)
Пример:
зеркалирование фигуры относительно
прямой Х=0: M (X=0)
A
B
C
2
1
1
-1
0
0
5
1
1
1
0
3
4
1
* 0
0
1
Д
0
Оп
=
-2
1
1
-5
1
1
-3
4
1
Д’
Примечание: существует множество различных матриц для разных случаев зеркалирования
A’
B’
C’

20.

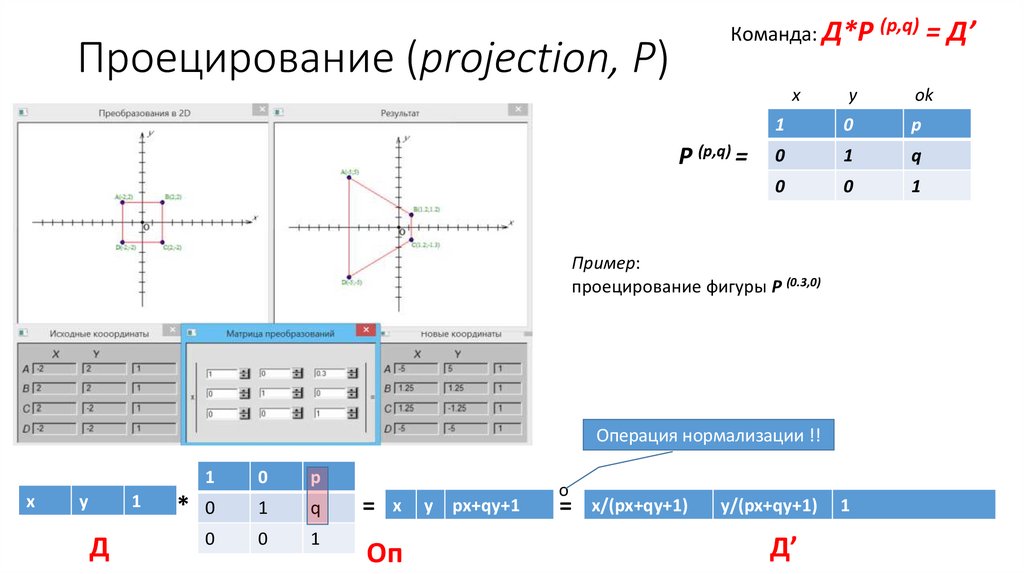
Команда: Д*P (p,q) = Д’
Проецирование (projection, P)
x
P (p,q) =
y
ok
1
0
p
0
1
q
0
0
1
Пример:
проецирование фигуры P (0.3,0)
Операция нормализации !!
1
x
y
1
Д
0
p
* 0
1
q
=
0
0
1
Оп
x
y
px+qy+1
o
=
x/(px+qy+1)
y/(px+qy+1)
Д’
1

21.

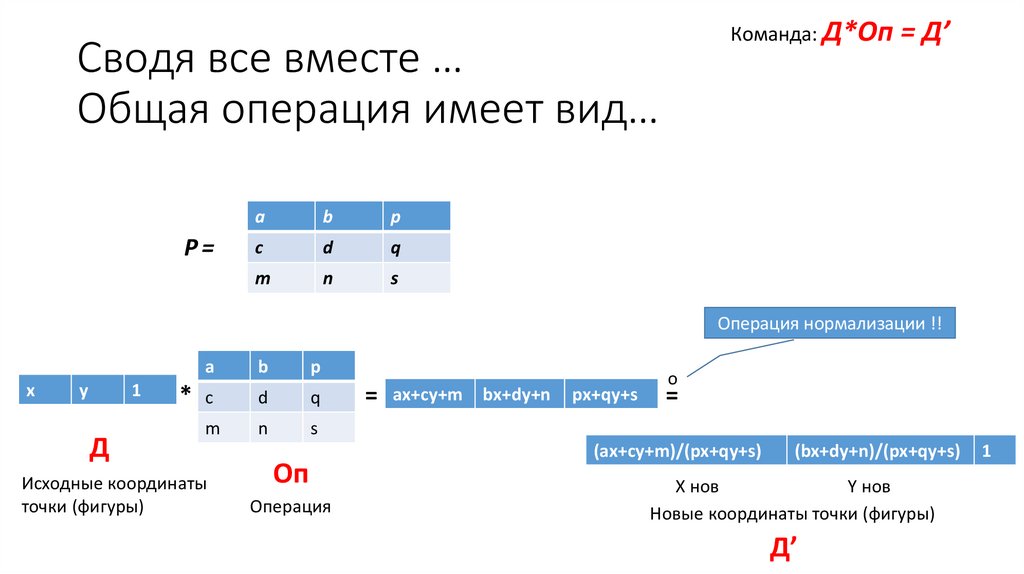
Команда: Д*Оп = Д’
Сводя все вместе …
Общая операция имеет вид…
P=
a
b
p
c
d
q
m
n
s
Операция нормализации !!
a
x
y
1
Д
b
p
* c
d
q
m
n
s
Исходные координаты
точки (фигуры)
Оп
Операция
=
ax+cy+m
bx+dy+n
px+qy+s
o
=
(ax+cy+m)/(px+qy+s)
(bx+dy+n)/(px+qy+s)
Х нов
Y нов
Новые координаты точки (фигуры)
Д’
1

22.

Про то, как действия в пространстве, определяют физику мира.
Дополнительная информация
для общего развития
• Симметрия законов природы во времени соответствует закону сохранения энергии.
• Симметрия законов природы по отношению к их переносам в пространстве
соответствует закону сохранения импульса.
• Симметрия законов природы по отношению к поворотам в пространстве
соответствует закону сохранения момента импульса.
• То есть законы сохранения энергии, импульса, момента импульса есть прямое
следствие определенных симметрий законов природы. Более общего понятия!
Интересно: simple*basic
Природа: m*a
Сущность * Действие
Сущность – это поле, проводимость действия
Взаимодействие – скалярное произведение
Скалярное произведение – это косинус

23.

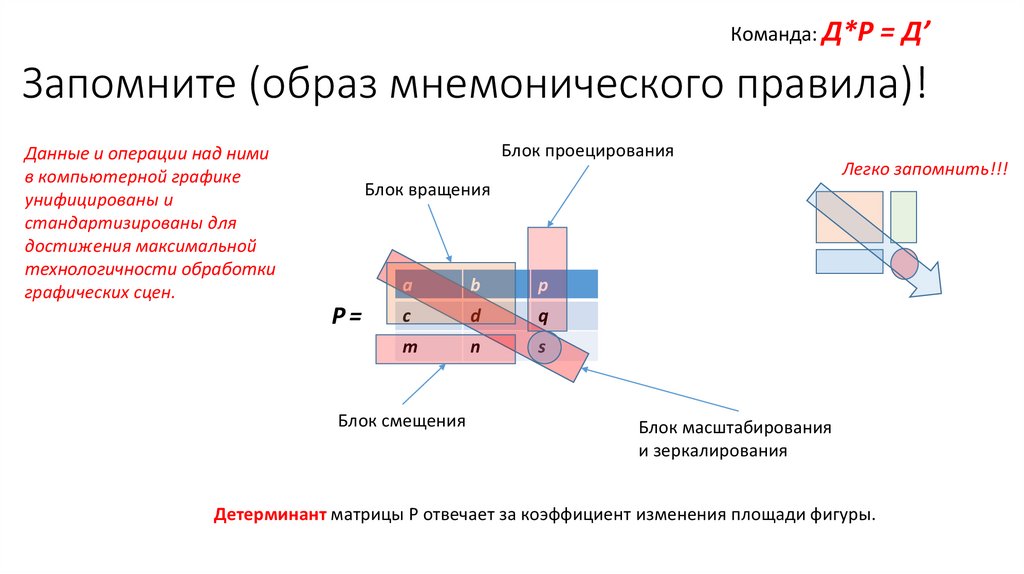
Команда: Д*P = Д’
Запомните (образ мнемонического правила)!
Блок проецирования
Данные и операции над ними
в компьютерной графике
унифицированы и
стандартизированы для
достижения максимальной
технологичности обработки
графических сцен.
Легко запомнить!!!
Блок вращения
P=
a
b
p
c
d
q
m
n
s
Блок смещения
Блок масштабирования
и зеркалирования
Детерминант матрицы Р отвечает за коэффициент изменения площади фигуры.

24.

• При аффинных преобразованиях точки преобразуются в точки, прямые - в прямые,
углы - в углы, площади - в площади.
• Следствие: достаточно просчитать ключевые точки изображения (вершины) и
соединить их прямыми линиями, чтобы получить все изображение. Это значительно
сокращает время вычислений.
• Любая задача геометрических преобразований решается единообразно «матричным
способом».
• Все сводится к преобразованию матриц.
• Базовые геометрические операции – умножение матриц, сложение матриц,
вычисление детерминанта, вычисление обратной матрицы, транспонирование.
• Логично создать матричный процессор для одномоментного действия над матрицей
чисел (графическое действие над геометрическим объектом).

25.

Информация для продвинутых студентов
Преобразования
Евклидово < Аффинное < Проективное
(перспективное)
Cos(a)
Sin(a)
0
Cos(a)
Sin(a)
0
Cos(a)
Sin(a)
P
- Sin(a)
Cos(a)
0
- Sin(a)
Cos(a)
0
- Sin(a)
Cos(a)
q
m
n
1
m
n
s
m
n
1
Твердое тело без деформаций,
сдвиг и поворот без
масштабирования
Сохранение прямых линий,
сохранение отношений длин
отрезков и отношений площадей,
параллельные переходят в
параллельные, есть деформация
тел, наличие одной неподвижной
точки.
Преобразование Т не сохраняет
параллельные линии,
три точки, лежащие на одной
прямой, после преобразования
Т остаются на одной прямой
Нелинейные уравнения становятся линейными после введения однородных координат!!!

26.

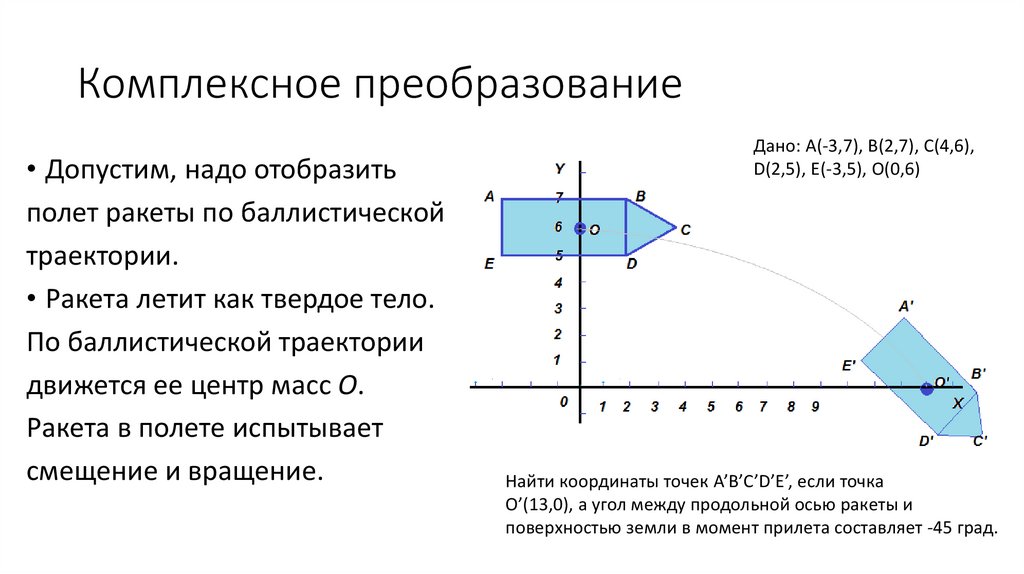
Комплексное преобразование
• Допустим, надо отобразить
полет ракеты по баллистической
траектории.
• Ракета летит как твердое тело.
По баллистической траектории
движется ее центр масс О.
Ракета в полете испытывает
смещение и вращение.
Дано: A(-3,7), B(2,7), C(4,6),
D(2,5), E(-3,5), O(0,6)
Найти координаты точек A’B’C’D’E’, если точка
О’(13,0), а угол между продольной осью ракеты и
поверхностью земли в момент прилета составляет -45 град.

27.

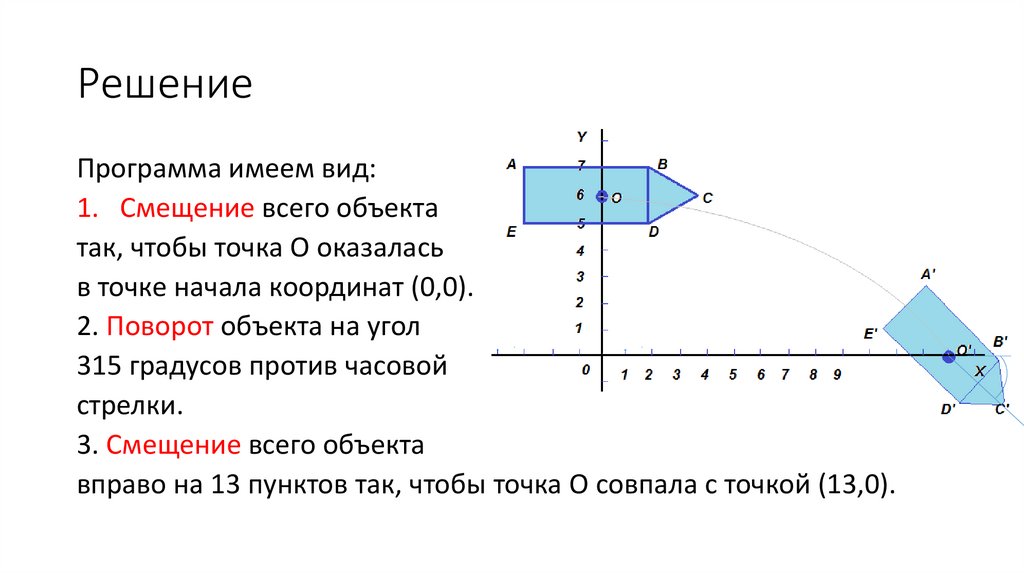
Решение
Программа имеем вид:
1. Смещение всего объекта
так, чтобы точка О оказалась
в точке начала координат (0,0).
2. Поворот объекта на угол
315 градусов против часовой
стрелки.
3. Смещение всего объекта
вправо на 13 пунктов так, чтобы точка О совпала с точкой (13,0).

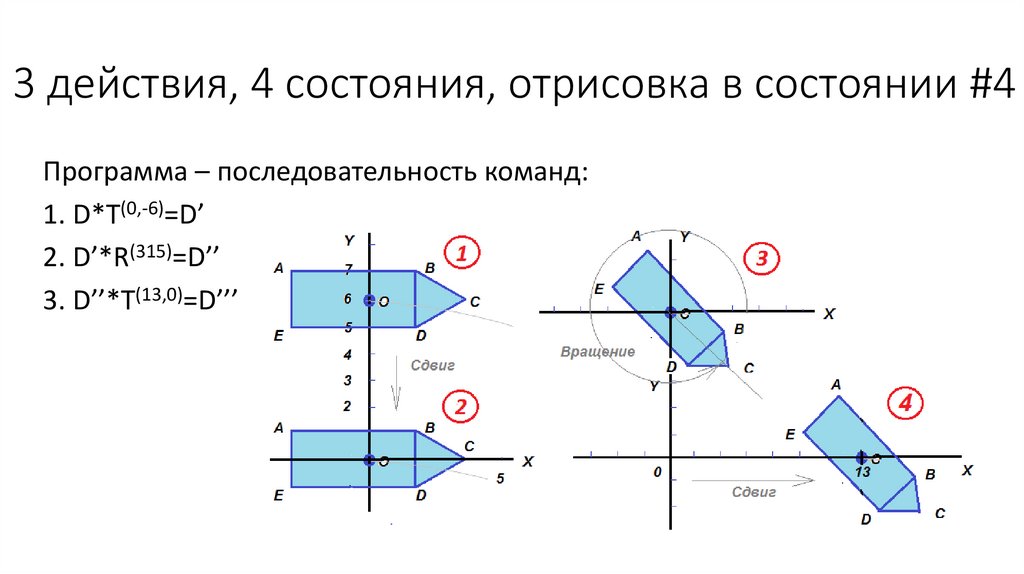
28.

3 действия, 4 состояния, отрисовка в состоянии #4
Программа – последовательность команд:
1. D*Т(0,-6)=D’
2. D’*R(315)=D’’
3. D’’*T(13,0)=D’’’

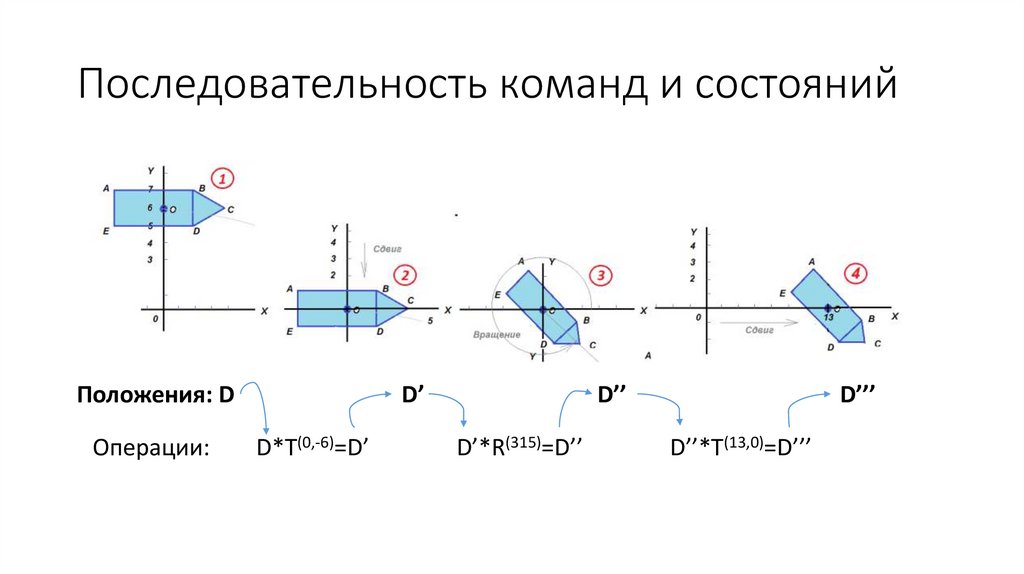
29.

Последовательность команд и состояний
Положения: D
Операции:
D’
D*Т(0,-6)=D’
D’’
D’*R(315)=D’’
D’’’
D’’*T(13,0)=D’’’

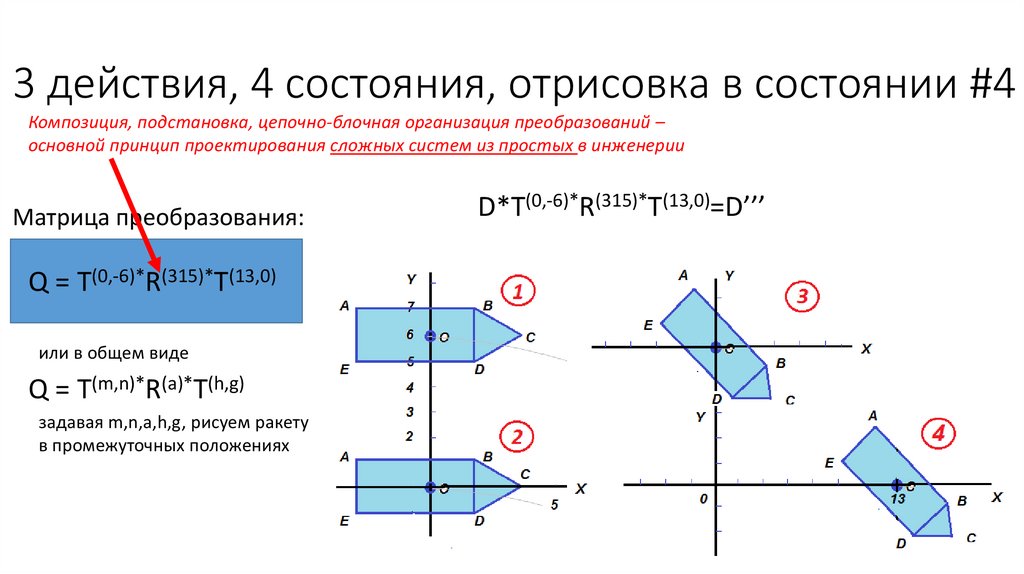
30.

3 действия, 4 состояния, отрисовка в состоянии #4
Композиция, подстановка, цепочно-блочная организация преобразований –
основной принцип проектирования сложных систем из простых в инженерии
Матрица преобразования:
Q = Т(0,-6)*R(315)*T(13,0)
или в общем виде
Q = Т(m,n)*R(a)*T(h,g)
задавая m,n,a,h,g, рисуем ракету
в промежуточных положениях
D*Т(0,-6)*R(315)*T(13,0)=D’’’

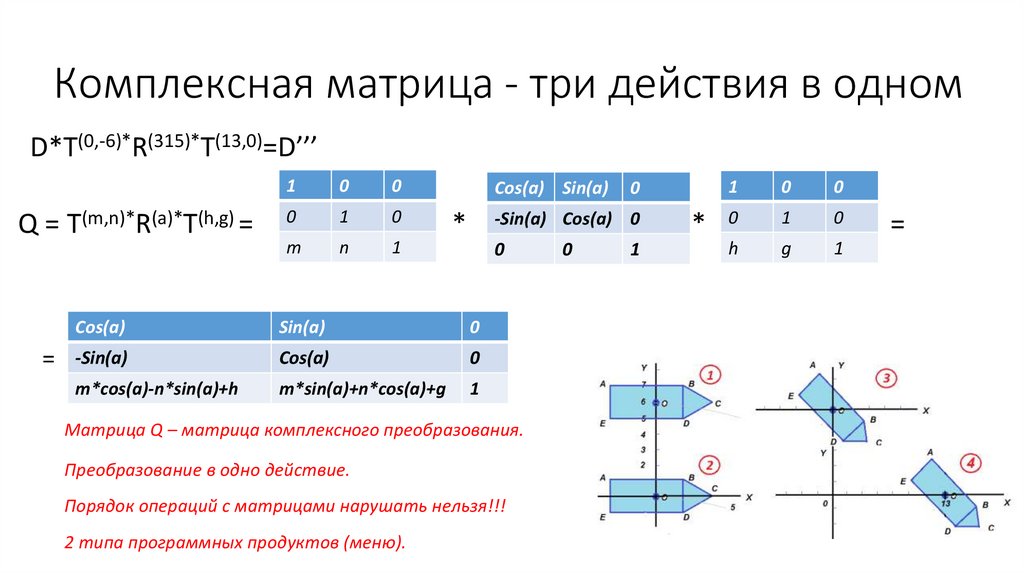
31.

Комплексная матрица - три действия в одном
D*Т(0,-6)*R(315)*T(13,0)=D’’’
Q = Т(m,n)*R(a)*T(h,g) =
=
1
0
0
0
1
0
m
n
1
Cos(a) Sin(a)
-Sin(a) Cos(a) 0
*
0
Cos(a)
Sin(a)
0
-Sin(a)
Cos(a)
0
m*cos(a)-n*sin(a)+h
m*sin(a)+n*cos(a)+g
1
Матрица Q – матрица комплексного преобразования.
Преобразование в одно действие.
Порядок операций с матрицами нарушать нельзя!!!
2 типа программных продуктов (меню).
0
0
1
*
1
0
0
0
1
0
h
g
1
=

32.

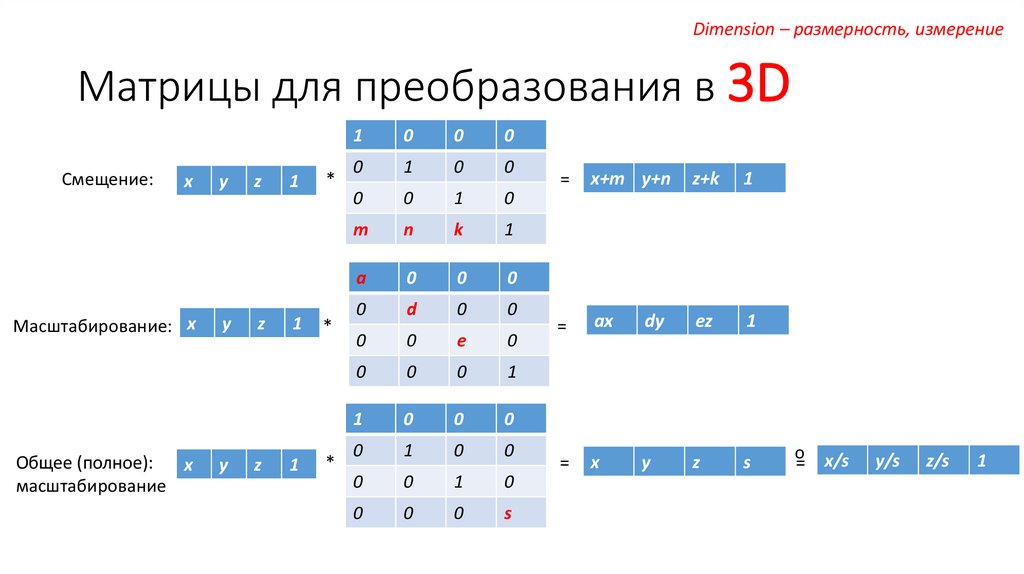
Dimension – размерность, измерение
Матрицы для преобразования в 3D
Смещение:
x
Масштабирование: x
Общее (полное):
x
масштабирование
y
y
y
z
z
z
1
1
1
*
*
*
1
0
0
0
0
1
0
0
0
0
1
0
m
n
k
1
a
0
0
0
0
d
0
0
0
0
e
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
s
=
x+m y+n
z+k
1
=
ax
dy
ez
1
=
x
y
z
s
o
=
x/s
y/s
z/s
1

33.

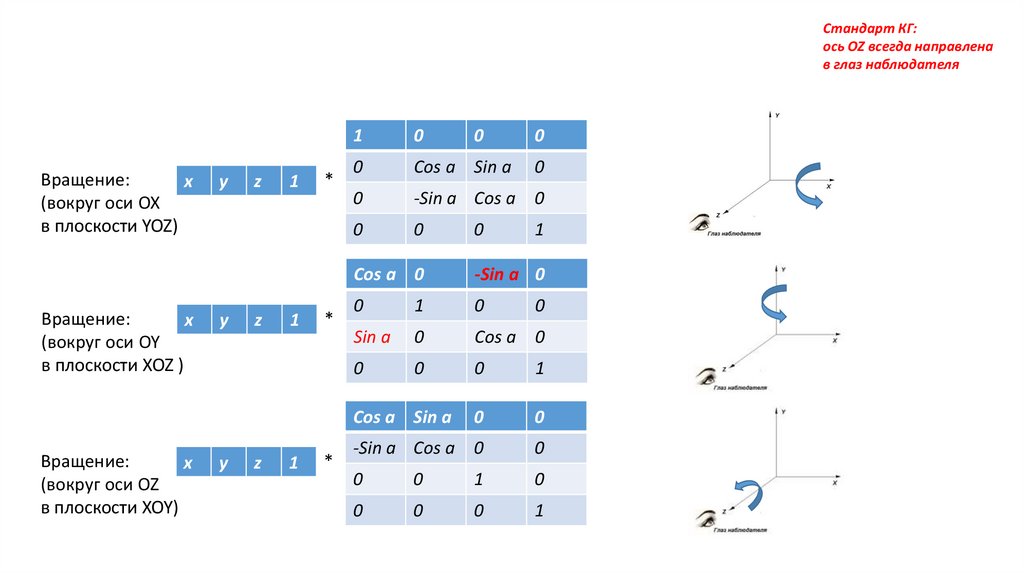
Стандарт КГ:
ось OZ всегда направлена
в глаз наблюдателя
Вращение:
x
(вокруг оси OX
в плоскости YOZ)
Вращение:
x
(вокруг оси OY
в плоскости XOZ )
y
y
z
z
1
1
*
*
1
0
0
Cos a Sin a
0
-Sin a Cos a 0
0
0
y
z
1
*
0
0
0
1
Cos a 0
-Sin a 0
0
1
0
Sin a
0
Cos a 0
0
0
0
1
0
0
-Sin a Cos a 0
0
0
0
1
0
0
0
0
1
Cos a Sin a
Вращение:
x
(вокруг оси OZ
в плоскости XOY)
0
0

34.

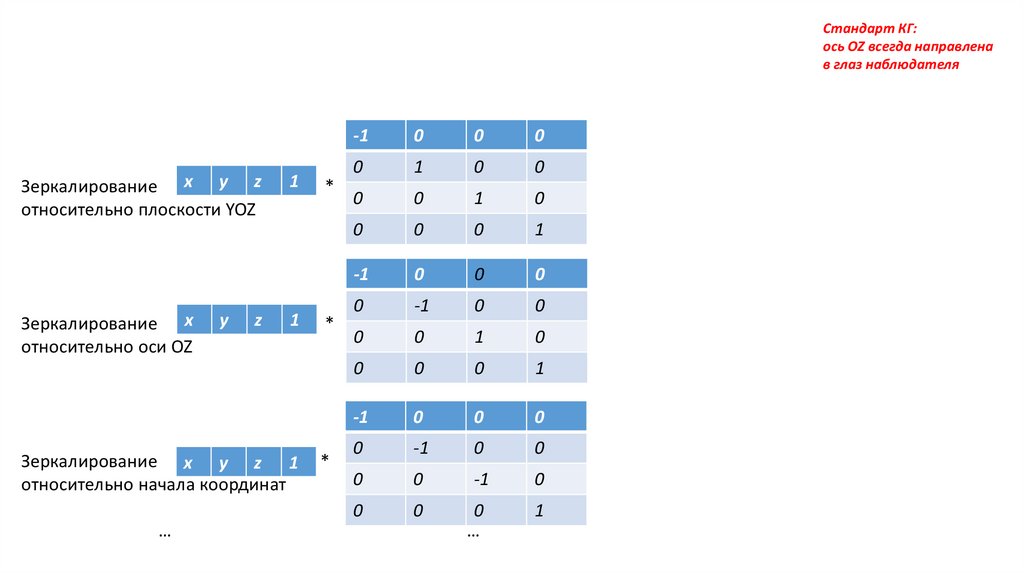
Стандарт КГ:
ось OZ всегда направлена
в глаз наблюдателя
Зеркалирование x y z
относительно плоскости YOZ
Зеркалирование x
относительно оси OZ
y
z
1
1
Зеркалирование x y z 1
относительно начала координат
…
*
*
*
-1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
-1
0
0
0
0
-1
0
0
0
0
1
0
0
0
0
1
-1
0
0
0
0
-1
0
0
0
0
-1
0
0
0
0
…
1

35.

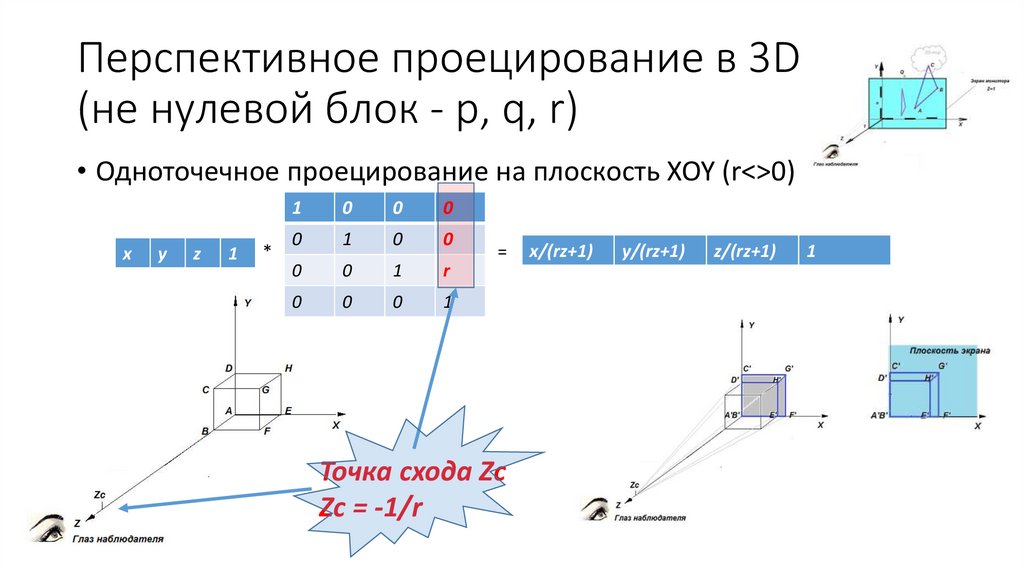
Перспективное проецирование в 3D
(не нулевой блок - p, q, r)
• Одноточечное проецирование на плоскость XOY (r<>0)
x
y
z
1
*
1
0
0
0
0
1
0
0
0
0
1
r
0
0
0
1
=
Точка схода Zc
Zc = -1/r
x/(rz+1)
y/(rz+1)
z/(rz+1)
1

36.

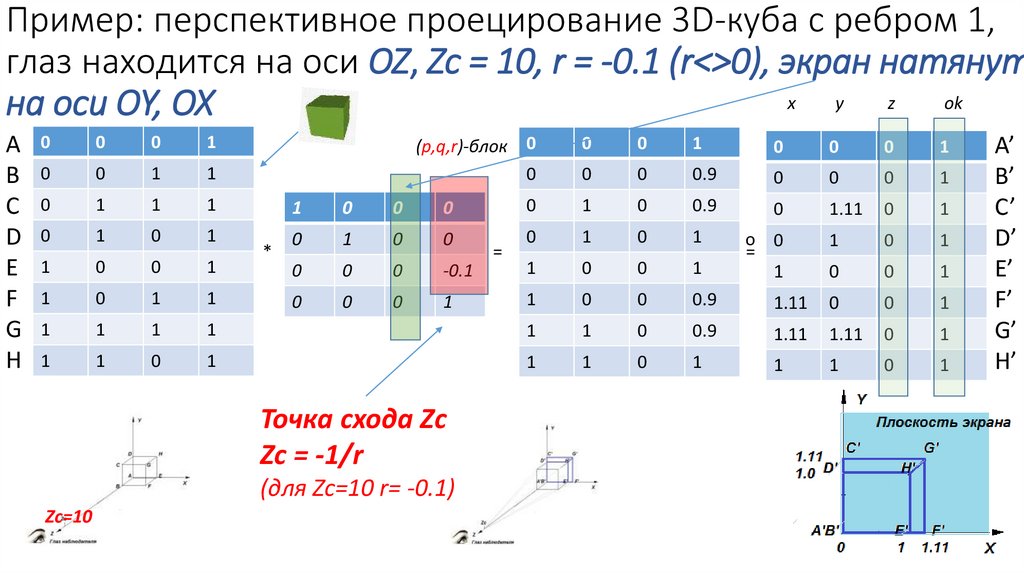
Пример: перспективное проецирование 3D-куба с ребром 1,
глаз находится на оси OZ, Zc = 10, r = -0.1 (r<>0), экран натянут
x
y
z
ok
на оси OY, OX
A
B
C
D
E
F
G
H
0
0
0
1
0
0
1
1
0
1
1
1
0
1
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
0
(p,q,r)-блок 0
0
0
0
1
0
0
0
1
0
0
0.9
0
0
0
1
0
1
0
0.9
0
1.11
0
1
0
1
0
1
1
0
1
1
0
0
1
0
0
1
1
0
0
0.9
1.11
0
0
1
1
1
1
0
0.9
1.11
1.11
0
1
1
1
1
0
1
1
1
0
1
*
1
0
0
0
0
1
0
0
0
0
0
-0.1
0
0
0
1
Точка схода Zc
Zc = -1/r
(для Zc=10 r= -0.1)
Zс=10
=
o 0
=
1
A’
B’
C’
D’
E’
F’
G’
H’

37.

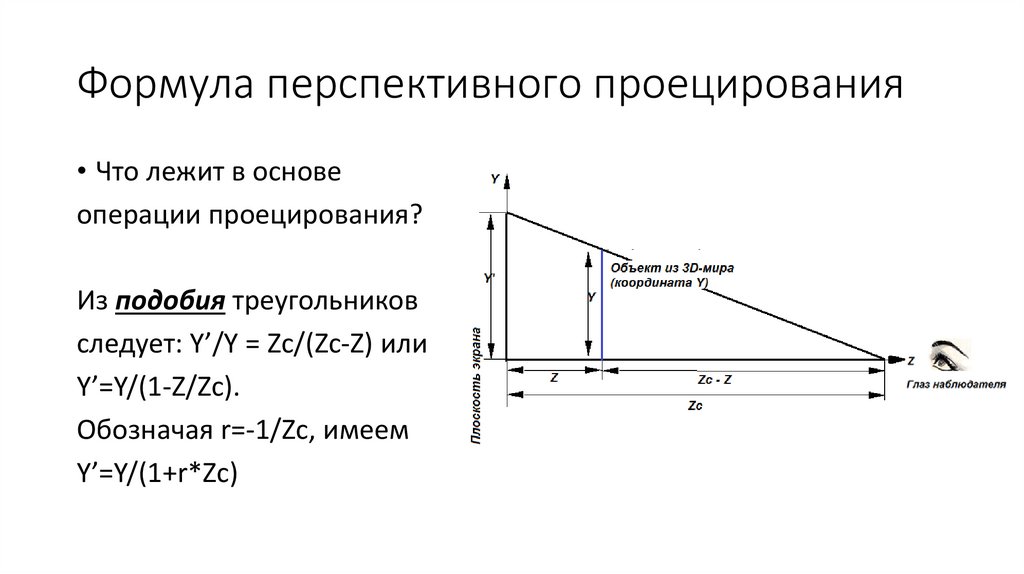
Формула перспективного проецирования
• Что лежит в основе
операции проецирования?
Из подобия треугольников
следует: Y’/Y = Zc/(Zc-Z) или
Y’=Y/(1-Z/Zc).
Обозначая r=-1/Zc, имеем
Y’=Y/(1+r*Zc)

38.

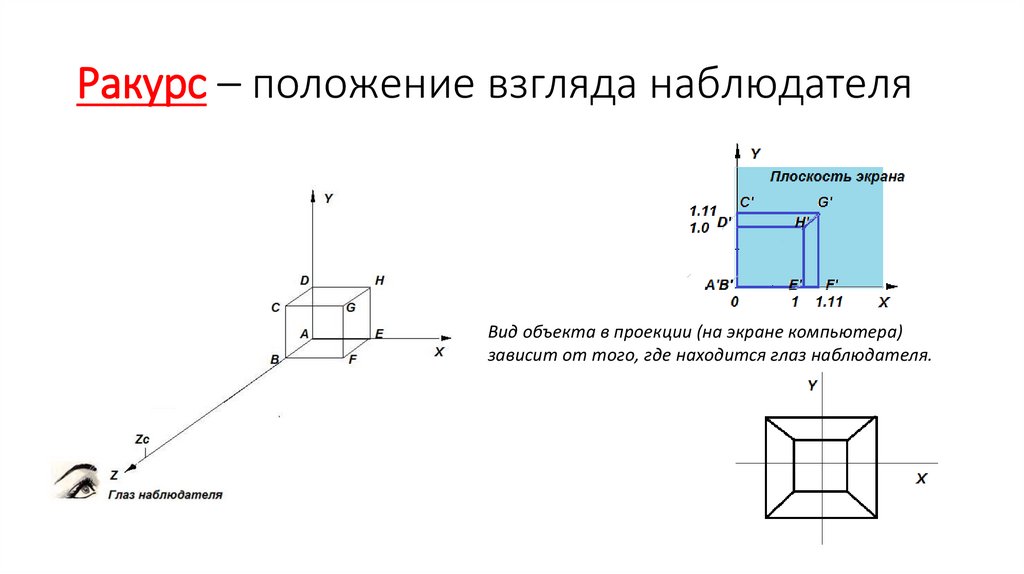
Ракурс – положение взгляда наблюдателя
Вид объекта в проекции (на экране компьютера)
зависит от того, где находится глаз наблюдателя.

39.

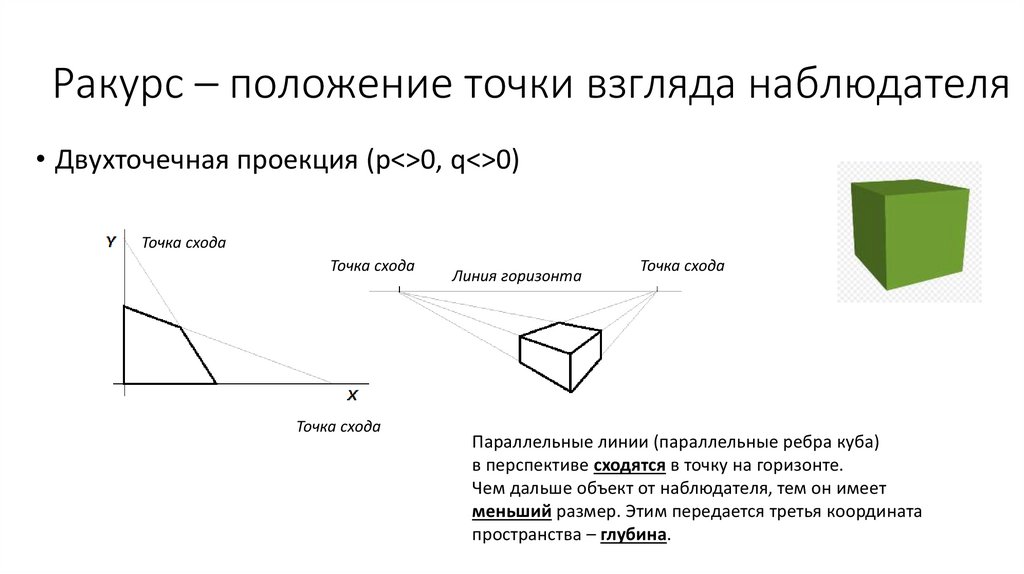
Ракурс – положение точки взгляда наблюдателя
• Двухточечная проекция (p<>0, q<>0)
Точка схода
Точка схода
Точка схода
Линия горизонта
Точка схода
Параллельные линии (параллельные ребра куба)
в перспективе сходятся в точку на горизонте.
Чем дальше объект от наблюдателя, тем он имеет
меньший размер. Этим передается третья координата
пространства – глубина.

40.

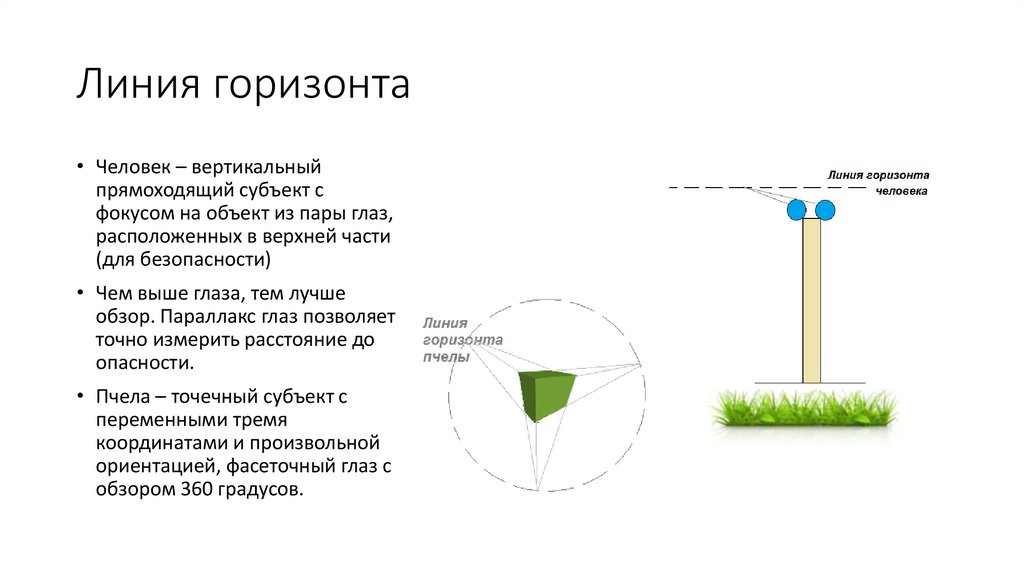
Линия горизонта
• Человек – вертикальный
прямоходящий субъект с
фокусом на объект из пары глаз,
расположенных в верхней части
(для безопасности)
• Чем выше глаза, тем лучше
обзор. Параллакс глаз позволяет
точно измерить расстояние до
опасности.
• Пчела – точечный субъект с
переменными тремя
координатами и произвольной
ориентацией, фасеточный глаз с
обзором 360 градусов.

41.

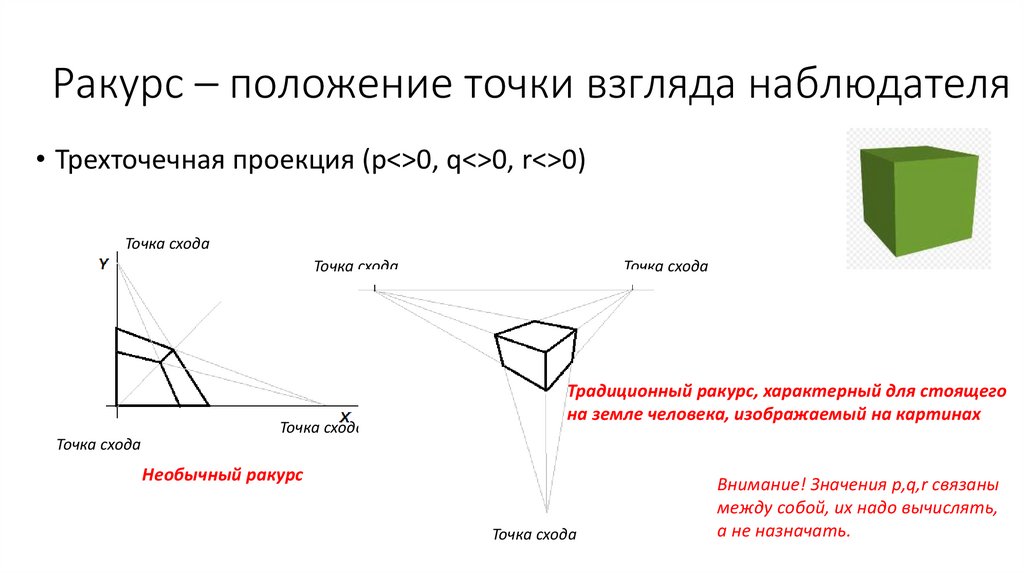
Ракурс – положение точки взгляда наблюдателя
• Трехточечная проекция (p<>0, q<>0, r<>0)
Точка схода
Точка схода
Точка схода
Точка схода
Точка схода
Линия горизонта
Традиционный ракурс, характерный для стоящего
на земле человека, изображаемый на картинах
Необычный ракурс
Точка схода
Внимание! Значения p,q,r связаны
между собой, их надо вычислять,
а не назначать.

42.

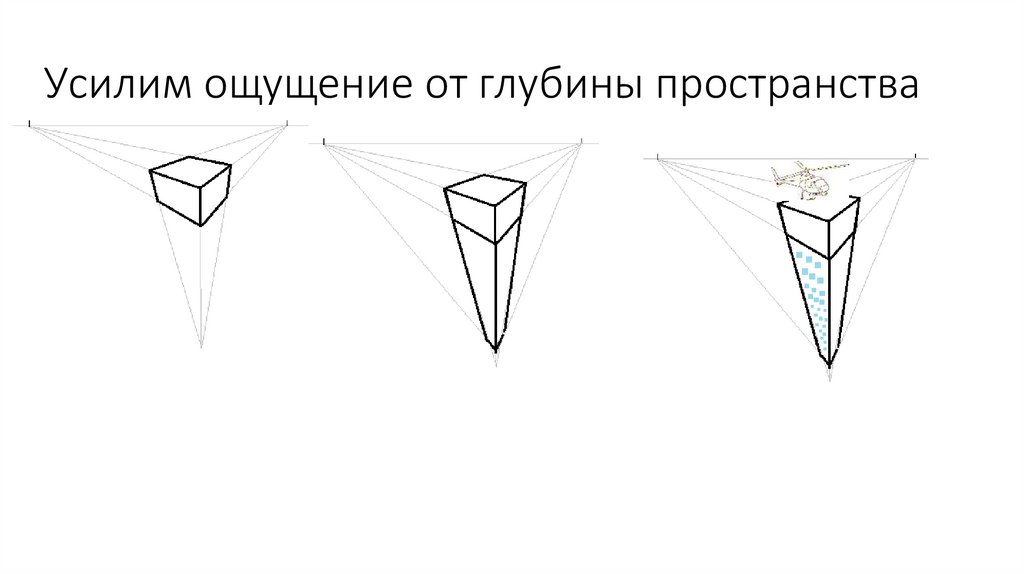
Усилим ощущение от глубины пространства

43.

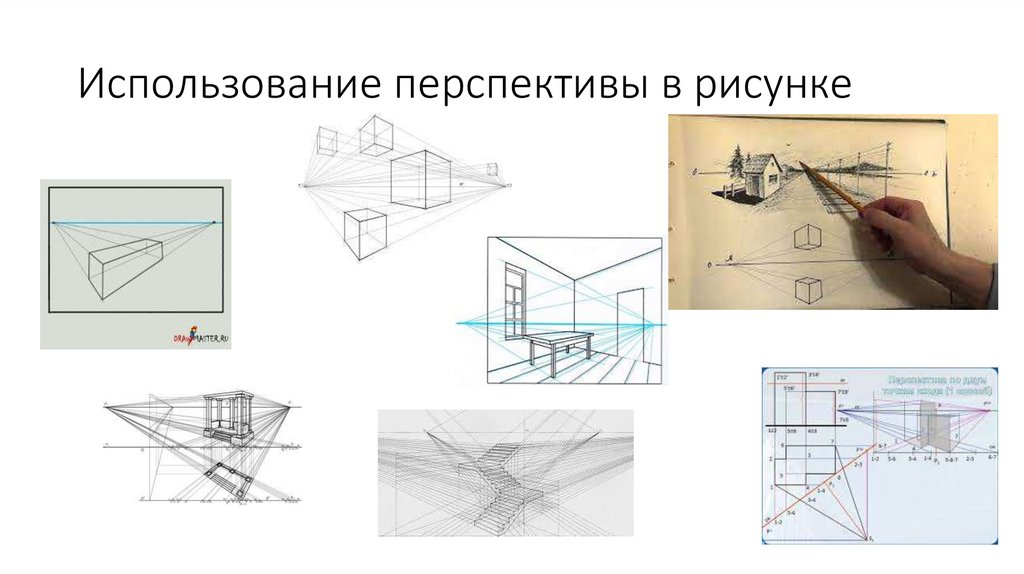
Использование перспективы в рисунке

44.

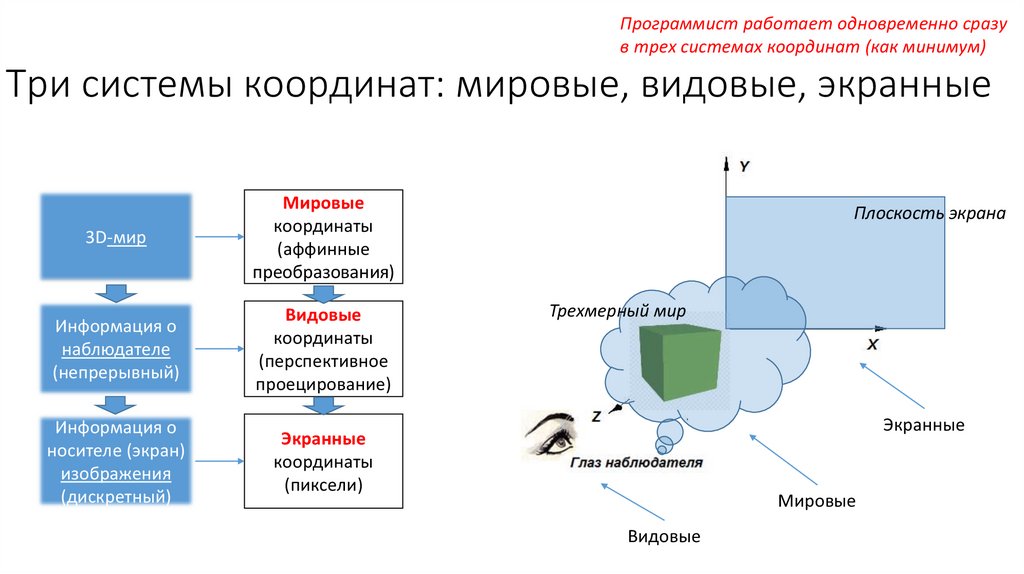
Программист работает одновременно сразу
в трех системах координат (как минимум)
Три системы координат: мировые, видовые, экранные
3D-мир
Мировые
координаты
(аффинные
преобразования)
Информация о
наблюдателе
(непрерывный)
Видовые
координаты
(перспективное
проецирование)
Информация о
носителе (экран)
изображения
(дискретный)
Экранные
координаты
(пиксели)
Плоскость экрана
Трехмерный мир
Экранные
Мировые
Видовые

45.

Экранные координаты
• Задача:
отразить область
(b-a, d-c) в
область на экране
(x2-x1,y2-y1) и
объект (g,h) в его образ на экране с
координатами (x,y)
1. Коэффициенты
масштабирования:
fx=(x2-x1)/(b-a), fy=(y2-y1)/(d-c)
2. F=min(fx,fy)
• fx<>fy – искажение формы
(углов), полное использование
пространства экрана
3D-мир и объект (g,h)
• fx=fy – сохранение формы,
fx
использование части
пространства экрана
3. x=x1+fx*(g-a), y=y1+fy*(h-c) , так как
Плоскость экрана и
образ объекта (x,y)

46.

Были ли американцы на Луне?
Матричный метод - универсальный метод.
Прикладные задачи
• Восстановление трехмерных координат объекта по двум проекциям
(фото) в судебных экспертизах – решение обратной задачи
x
y
z
1
*F=
неизвестные величины
x’
y’
0
1
заданные значения
Найти F
• Тени на фотографиях с Луны
• Проецирование «Бука» и домов на дороге на видео конфликта на
Украине
Является ли видео с ПЗРК «Бук» на дорогах
Донбасса подделкой в деле о сбитом МН17?

47.

Примеры разоблачений фейков специалистами
по графике
Почему на теневой стороне в стекле скафандра видно отражение?
Почему тени направлены в разные стороны?
Почему не совпадают точки схода?
Почему у равных по росту космонавтов длина тени разная?

48.

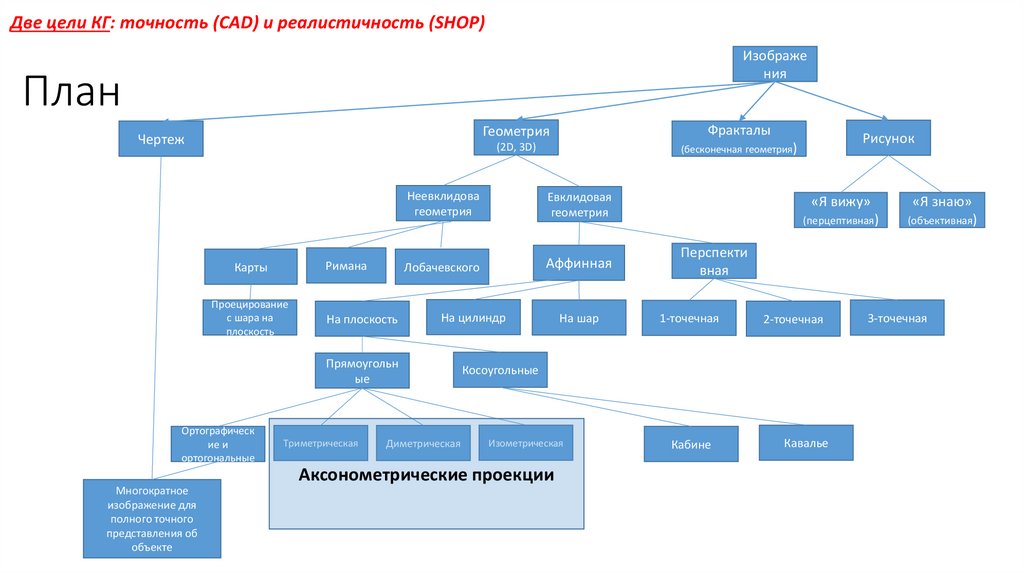
Две цели КГ: точность (CAD) и реалистичность (SHOP)
Изображе
ния
План
Чертеж
Римана
Карты
Проецирование
с шара на
плоскость
На плоскость
Триметрическая
Фракталы
(2D, 3D)
(бесконечная геометрия)
Неевклидова
геометрия
Евклидовая
геометрия
Лобачевского
Аффинная
На цилиндр
Прямоугольн
ые
Ортографическ
ие и
ортогональные
Геометрия
Диметрическая
«Я вижу»
«Я знаю»
(перцептивная)
(объективная)
Перспекти
вная
1-точечная
2-точечная
Кабине
Кавалье
Косоугольные
Изометрическая
Аксонометрические проекции
Многократное
изображение для
полного точного
представления об
объекте
На шар
Рисунок
3-точечная

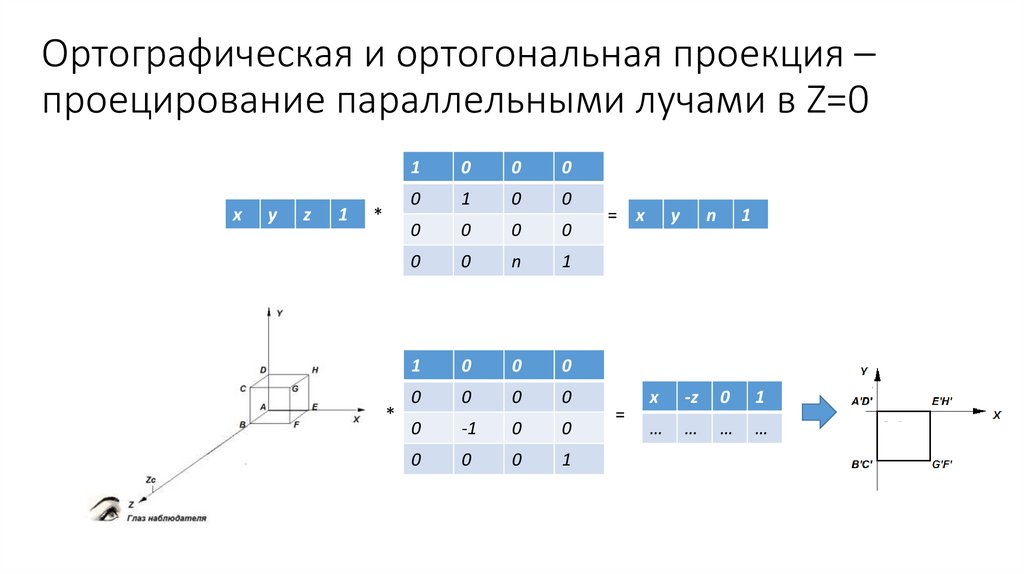
49.

Ортографическая и ортогональная проекция –
проецирование параллельными лучами в Z=0
x
y
z
1
*
*
1
0
0
0
0
1
0
0
0
0
0
0
0
0
n
1
1
0
0
0
0
0
0
0
0
-1
0
0
0
0
0
1
= x
=
y
n
1
x
-z
0
1
…
…
…
…

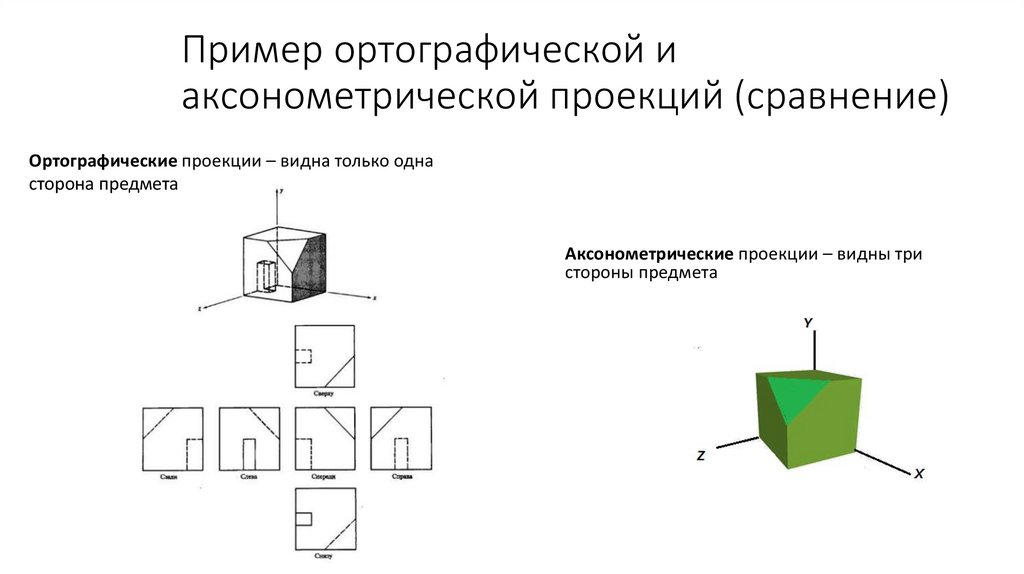
50.

Пример ортографической и
аксонометрической проекций (сравнение)
Ортографические проекции – видна только одна
сторона предмета
Аксонометрические проекции – видны три
стороны предмета

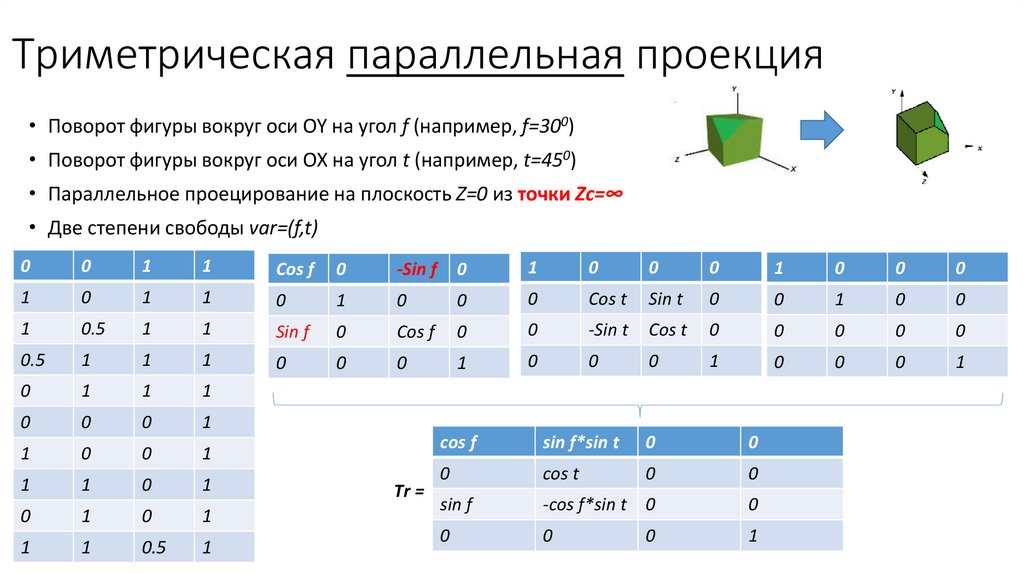
51.

Триметрическая параллельная проекция
• Поворот фигуры вокруг оси OY на угол f (например, f=300)
• Поворот фигуры вокруг оси OX на угол t (например, t=450)
• Параллельное проецирование на плоскость Z=0 из точки Zc=∞
• Две степени свободы var=(f,t)
0
0
1
1
Cos f
0
-Sin f
0
1
0
0
0
1
0
0
0
1
0
1
1
0
1
0
0
0
Cos t
Sin t
0
0
1
0
0
1
0.5
1
1
Sin f
0
Cos f
0
0
-Sin t
Cos t
0
0
0
0
0
0.5
1
1
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
0
0
0
1
1
0
0
1
cos f
sin f*sin t
0
0
1
1
0
1
0
cos t
0
0
0
1
0
1
sin f
-cos f*sin t 0
0
1
1
0.5
1
0
0
1
Тr =
0

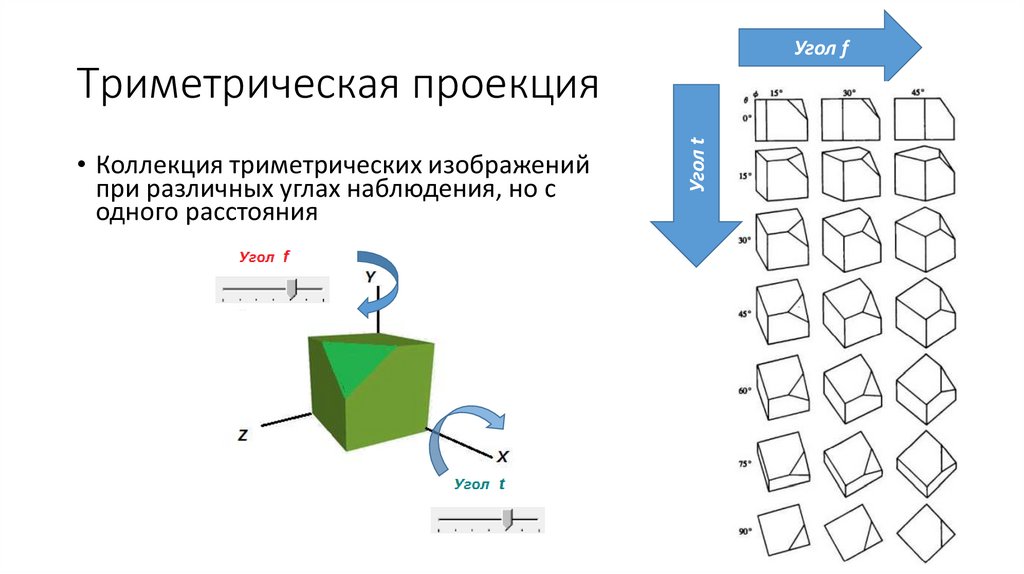
52.

Угол f
• Коллекция триметрических изображений
при различных углах наблюдения, но с
одного расстояния
Угол t
Триметрическая проекция

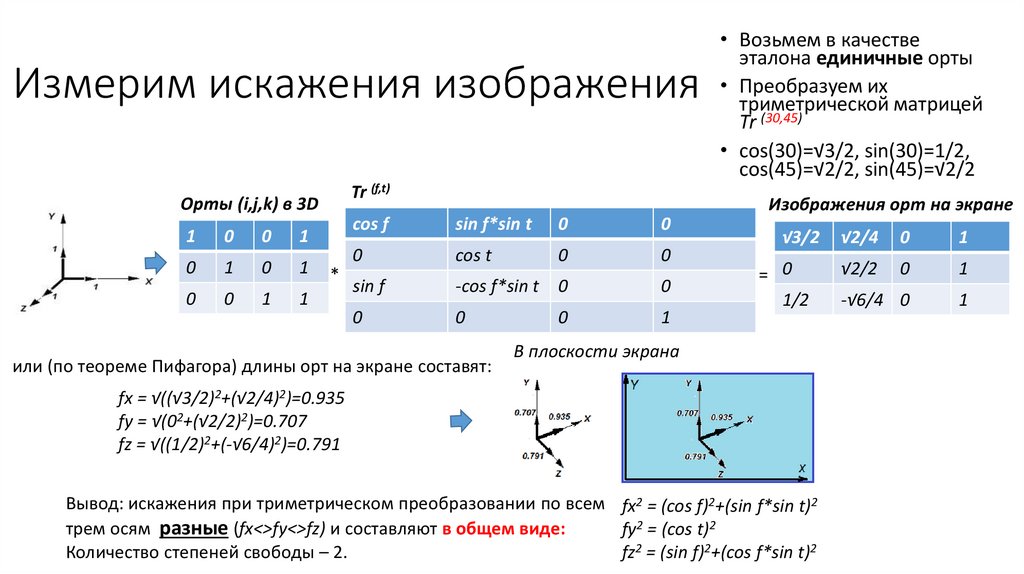
53.

Измерим искажения изображения
Tr (f,t)
Орты (i,j,k) в 3D
1
0
0
1
0
1
0
1
0
0
1
1
*
• Возьмем в качестве
эталона единичные орты
• Преобразуем их
триметрической матрицей
Tr (30,45)
• cos(30)=√3/2, sin(30)=1/2,
cos(45)=√2/2, sin(45)=√2/2
Изображения орт на экране
cos f
sin f*sin t
0
0
0
cos t
0
0
sin f
-cos f*sin t 0
0
0
0
1
или (по теореме Пифагора) длины орт на экране составят:
0
√3/2
√2/4
0
1
= 0
1/2
√2/2
0
1
-√6/4 0
1
В плоскости экрана
fx = √((√3/2)2+(√2/4)2)=0.935
fy = √(02+(√2/2)2)=0.707
fz = √((1/2)2+(-√6/4)2)=0.791
Вывод: искажения при триметрическом преобразовании по всем fx2 = (cos f)2+(sin f*sin t)2
трем осям разные (fx<>fy<>fz) и составляют в общем виде:
fy2 = (cos t)2
Количество степеней свободы – 2.
fz2 = (sin f)2+(cos f*sin t)2

54.

Диметрическая проекция
(искажения по двум осям одинаковы)
• fx2 = (cos f)2+(sin f*sin t)2
• fy2 = (cos t)2
• fz2 = (sin f)2+(cos f*sin t)2
Количество степеней свободы
диметрической проекции равно 1:
fz
f
t
• Теперь допустим, что: fx=fy (ограничение, дополнительное условие)
Тогда: (cos f)2+(sin f*sin t)2 = (cos t)2
sin2f = sin2 t /(1- sin2 t)
fz2=2*sin2 t, fx2=fy2= cos2 t
t=arcsin(±fz/√2) и f=arcsin(±fz/√(2-fz2))
Задавая fz, имеем 4 изображения (f,t), у которых fx=fy.
Например, при fz=0.5 (удобный масштаб!!!) имеем
f=±22.208 град, t=±20.705 град.

55.

Изометрическая проекция
(искажения по всем трем осям равны)
Всего 4 изображения
• fx2 = (cos f)2+(sin f*sin t)2
• fy2 = (cos t)2
• fz2 = (sin f)2+(cos f*sin t)2
• Теперь допустим, что: fx=fy=fz (два дополнительных уравнения, два условия)
Тогда: (cos t)2 = 2(sin t)2
1-sin2 t = 2sin2 t
sin t=±√(1/3), t=±35.26 град.
sin2 f = sin2 t / (1-sin2t); sin2 f = ½; sin f= √2/2, f=±45 град.
fz2 = 2*(sin t)2 = 2/3
Имеем 4 изображения, у которых fx=fy=fz<>1.
Количество степеней свободы равно 0.
fx = fy = fz = √(2/3)
4 изображения, углы фиксированы.
Искажения по всем осям есть,
но они одинаковы (f=0.816)

56.

Триметрическая, диметрическая,
изометрическая проекции
При изменении параметров
проецирования триметрическая,
диметрическая и изометрическая
проекции плавно переходят
друг в друга
Вид проекции
Количество
изображений
Количество
степеней
свободы
Количество
ограничений
Параметры
Коэффициенты
искажения по
осям
Триметрия
∞*∞
2
-
f, t
fx<>fy<>fz<>1
Диметрия
4*∞
1
1
или f, или t
fx=fy<>fz
Изометрия
4
0
2
f=45, t=35.26
fx=fy=fz=0.82
fx2=fy2=fz2=2/3
Суммарное общее искажение изображения 3D-мира на 2D-плоскости равно: F22D=fx2+fy2+fz2=2/3+2/3+2/3=2,
F2D=√2.
В 3D F2=12+12+12=3, F3D=√3
Итого: F2D/F3D=√(2/3)
Вывод: ни при каких ракурсах невозможно изобразить трехмерные предметы на плоскости без искажений.
Суммарное искажение трехмерной сцены на двухмерном плоском изображении равно √(2/3) = 0.82.
Искажения неравномерно (кроме случая изометрии) распределены по изображению.

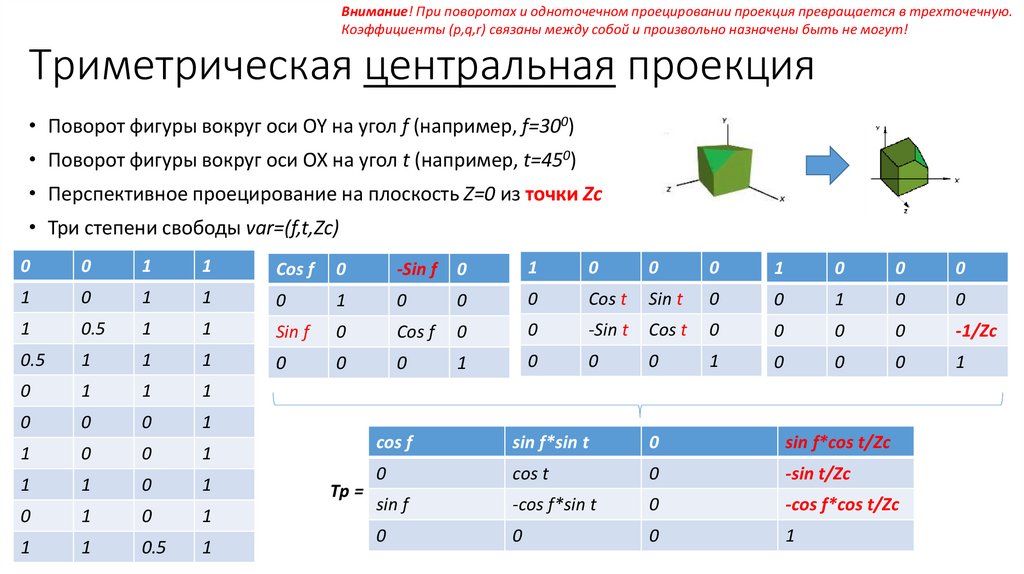
57.

Внимание! При поворотах и одноточечном проецировании проекция превращается в трехточечную.
Коэффициенты (p,q,r) связаны между собой и произвольно назначены быть не могут!
Триметрическая центральная проекция
• Поворот фигуры вокруг оси OY на угол f (например, f=300)
• Поворот фигуры вокруг оси OX на угол t (например, t=450)
• Перспективное проецирование на плоскость Z=0 из точки Zc
• Три степени свободы var=(f,t,Zc)
0
0
1
1
Cos f
0
-Sin f
0
1
0
0
0
1
0
0
0
1
0
1
1
0
1
0
0
0
Cos t
Sin t
0
0
1
0
0
1
0.5
1
1
Sin f
0
Cos f
0
0
-Sin t
Cos t
0
0
0
0
-1/Zc
0.5
1
1
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
0
0
0
1
1
0
0
1
cos f
sin f*sin t
0
sin f*cos t/Zc
1
1
0
1
0
cos t
0
-sin t/Zc
0
1
0
1
sin f
-cos f*sin t
0
-cos f*cos t/Zc
1
1
0.5
1
0
0
0
1
Тp =

58.

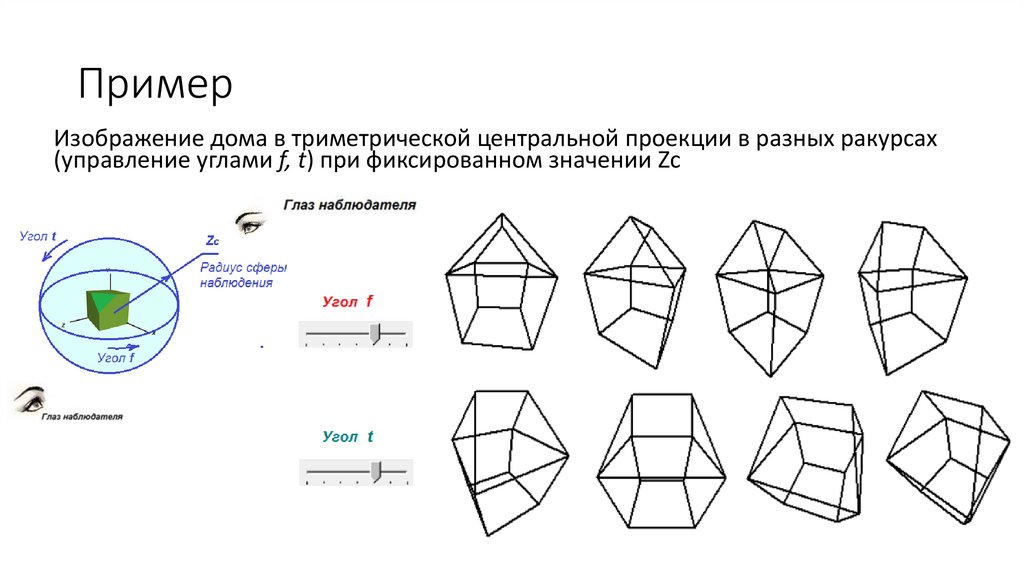
Пример
Изображение дома в триметрической центральной проекции в разных ракурсах
(управление углами f, t) при фиксированном значении Zc

59.

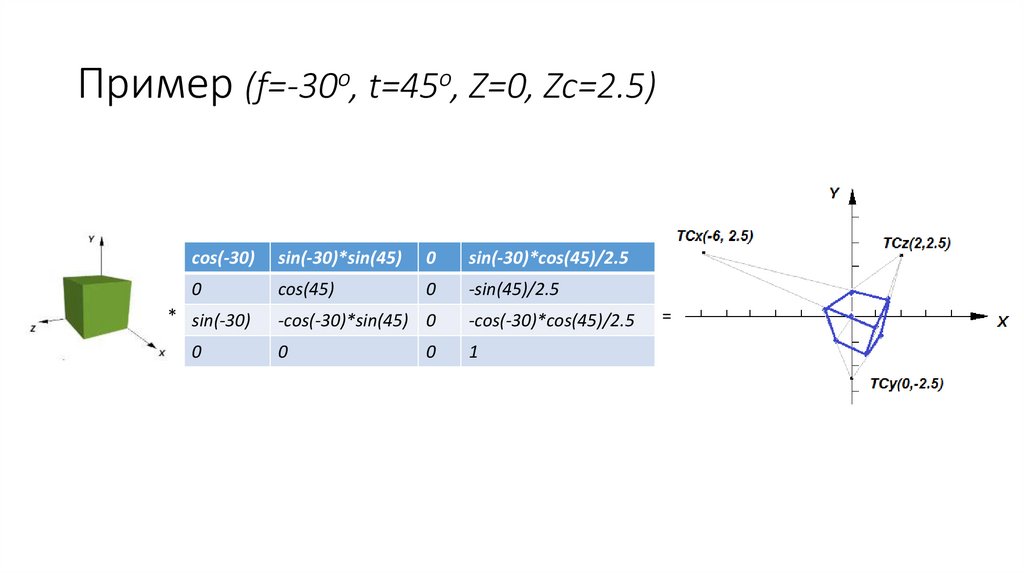
Пример (f=-30o, t=45o, Z=0, Zc=2.5)
cos(-30)
sin(-30)*sin(45)
0
sin(-30)*cos(45)/2.5
0
cos(45)
0
-sin(45)/2.5
* sin(-30)
0
-cos(-30)*sin(45) 0
-cos(-30)*cos(45)/2.5
0
1
0
=

60.

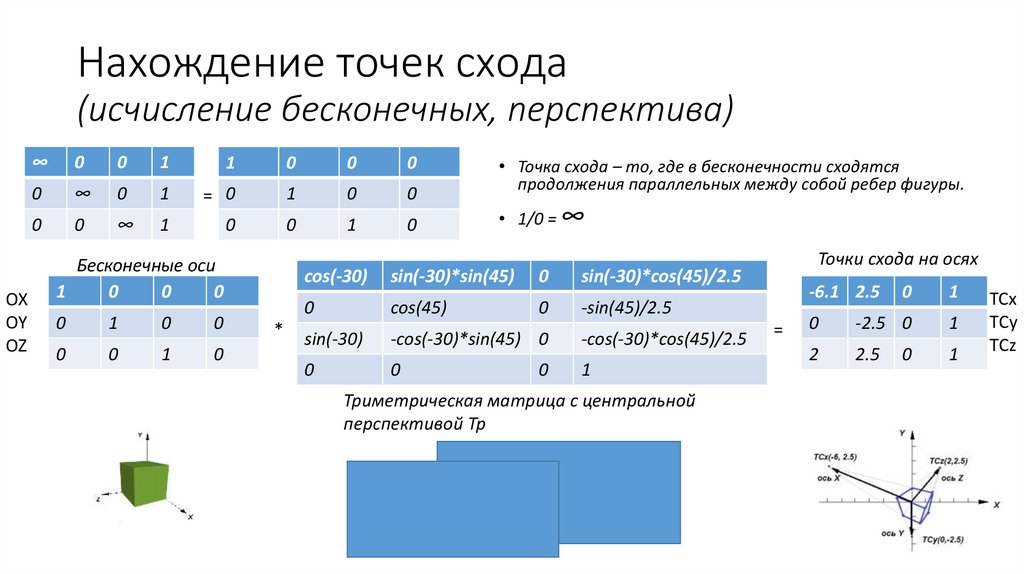
Нахождение точек схода
(исчисление бесконечных, перспектива)
OX
OY
OZ
∞
0
0
1
1
0
0
0
0
∞
0
1
= 0
1
0
0
0
0
∞
1
0
0
1
0
Бесконечные оси
1
0
0
0
0
1
0
0
0
0
1
0
*
• Точка схода – то, где в бесконечности сходятся
продолжения параллельных между собой ребер фигуры.
• 1/0 = ∞
cos(-30)
sin(-30)*sin(45)
0
sin(-30)*cos(45)/2.5
0
cos(45)
0
-sin(45)/2.5
sin(-30)
-cos(-30)*sin(45) 0
-cos(-30)*cos(45)/2.5
0
0
1
0
Триметрическая матрица с центральной
перспективой Tp
Точки схода на осях
-6.1 2.5
=
0
1
0
-2.5 0
1
2
2.5
1
0
ТСх
ТCy
TCz

61.

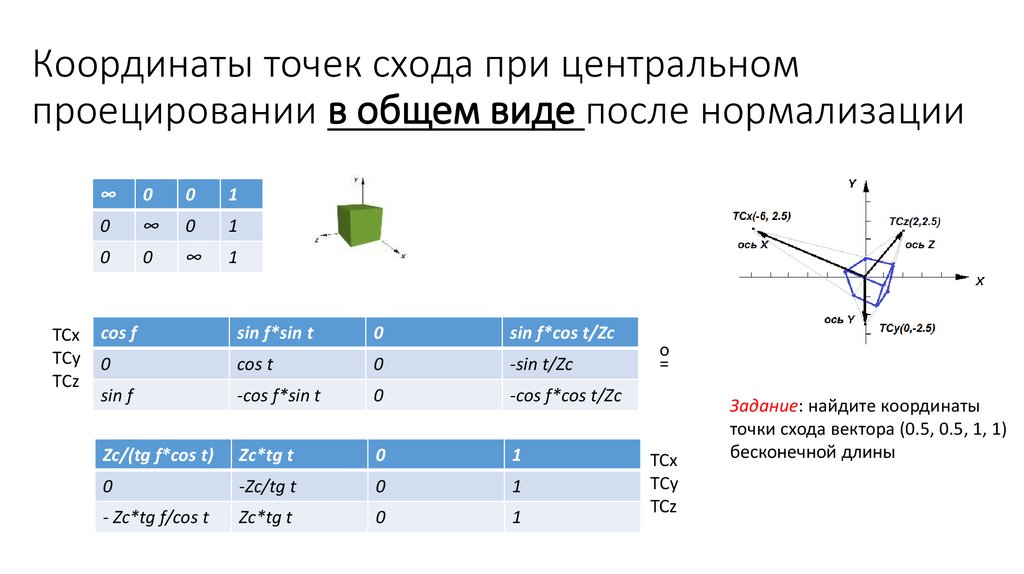
Координаты точек схода при центральном
проецировании в общем виде после нормализации
ТСх
ТCy
TCz
∞
0
0
1
0
∞
0
1
0
0
∞
1
cos f
sin f*sin t
0
sin f*cos t/Zc
0
cos t
0
-sin t/Zc
sin f
-cos f*sin t
0
-cos f*cos t/Zc
Zc/(tg f*cos t)
Zc*tg t
0
1
0
-Zc/tg t
0
1
- Zc*tg f/cos t
Zc*tg t
0
1
о
=
ТСх
ТCy
TCz
Задание: найдите координаты
точки схода вектора (0.5, 0.5, 1, 1)
бесконечной длины

62.

Положение экрана проецирования
Отметим интересную особенность матрицы перспективного проецирования.
Коэффициенты последнего столбца (блок коэффициентов проецирования) –
есть составляющие нормали к плоскости экрана, на который осуществляется
проецирование.
sin f*cos t/Zc *X + (-sin t/Zc)*Y + (-cos f*cos t/Zc)*Z + 1 = 0
или
sin f*cos t *X + (-sin t)*Y + (-cos f*cos t)*Z + Zc = 0.
Например, для случая f=-30o, t=45o, Z=0, Zc=2.5 имеем уравнение экрана:
0.35*X+0.71*Y+0.61*Z-2.5=0.
cos(-30)
sin(-30)*sin(45)
0
sin(-30)*cos(45)/2.5
0
cos(45)
0
-sin(45)/2.5
* sin(-30)
0
-cos(-30)*sin(45) 0
-cos(-30)*cos(45)/2.5
0
1
0
=
sin f*cos t/Zc
-sin t/Zc
-cos f*cos t/Zc
1

63.

Использование ракурса
• Сравните два
изображения Кристины
Орбакайте с разных
ракурсов.
• Обратите внимание на
длину носа.
• Используя ракурс, Вы
существенно можете
скрыть изъяны
изображаемого объекта

64.

Глубина
• Для осознания глубины пространства на его
изображении применяют: тени, штрихи,
окраску, стереоскопическую проекцию
На рис.1 не ясно, как высоко находится вертолет над поверхностью
.
На рис. 2 и 3 тень от объекта дает представление о третьей координате.

65.

Признаки глубины пространства
на плоскости изображения
• Схождение параллельных прямых в точку схода
• Относительные размеры знакомых объектов (дальше меньше)
• Перекрытие ближними предметами дальних
• Дальние предметы выше и правее (обычно)
• При движении глаза наблюдателя ближние предметы
двигаются быстрее, дальние – медленнее (параллакс
движения)
• Тени, штрихи, свет
• Воздушная перспектива (Леонардо да Винчи): вдали
ослабление атмосферного цвета голубым, исчезновение
мелких деталей, неровности контуров; отбрасывание
световых бликов (контрасты)
• Изменение усилия наружной мышцы глаза, вращающей
глазные яблоки

66.

STRATUM.AC.RU
[email protected]
[email protected]
CG
Computer graphics
MUHIN
© 2022, Stratum, О.И. Мухин (ссылка обязательна)