Similar presentations:
Динамика пассивного космического объекта при его бесконтактной транспортировке ионным потоком
1.
Динамика пассивногокосмического объекта при его
бесконтактной транспортировке
ионным потоком
В.С. Асланов,
А.С. Ледков
Самара, 2020
2.
Доклады на конференцияхV.S. Aslanov, A.S. Ledkov, "Chaotic motion of a passive space object during
its contactless transportation by ion beam", ITNT-2020, Samara
V.S. Aslanov, A.S. Ledkov, M. Konstantinov "Influence of space debris
attitude motion on ion beam assisted removal mission costs", IAC-2020,
Dubai
G. Popov, V.S. Aslanov, V. Petukhov, A.S. Ledkov, "Influence of space debris
attitude motion on ion beam assisted removal mission costs", IAC-2020,
Dubai
2
3.
Проблема космического мусораСиндром Кеслера – лавинообразное
увеличение числа обломков КМ
• 2007 – Разрушение Fengyun-1С
• 2009 - Столкновение Iridium 33 и Cosmos-2251
34000 объектов>10 cm
5400 объектов >1m
2000 активных спутников
US Space Surveillance Catalogue
Подходы к активному уделению
космического мусора:
• стыковка или жесткий захват
• захват и тросовая буксировка
• бесконтактная транспортировки
Donald J. Kessler
3
4.
Бесконтактное воздействие на объектБесконтактное взаимодействие:
• Электростатическое
• Гравитационное
• Ионный поток
• Магнитное
• Лазер
Преимущества
• Отсутствие механического
контакта
• Возможность транспортировки
быстро вращающихся
объектов
4
5.
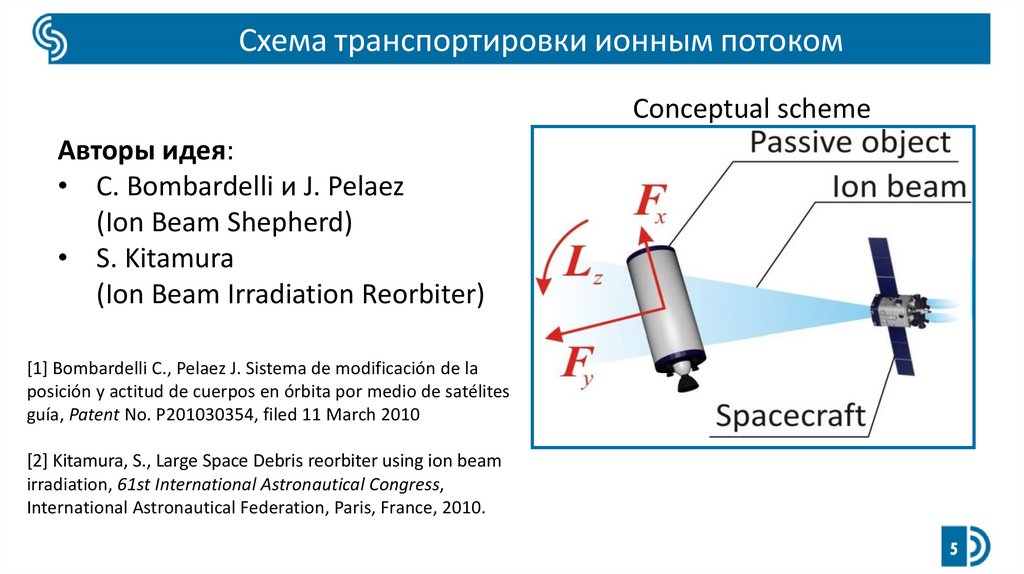
Схема транспортировки ионным потокомConceptual scheme
Авторы идея:
• C. Bombardelli и J. Pelaez
(Ion Beam Shepherd)
• S. Kitamura
(Ion Beam Irradiation Reorbiter)
[1] Bombardelli C., Pelaez J. Sistema de modificación de la
posición y actitud de cuerpos en órbita por medio de satélites
guía, Patent No. P201030354, filed 11 March 2010
[2] Kitamura, S., Large Space Debris reorbiter using ion beam
irradiation, 61st International Astronautical Congress,
International Astronautical Federation, Paris, France, 2010.
5
6.
Вычисление ионных сил и моментовd=15m =0
Fx Fx (d , , ) Fy Fy (d , , ) Lz Lz (d , , )
[3] A.P. Alpatov, S.V. Khoroshylov, A.I. Maslova, Contactless de-orbiting of space debris by the ion beam. Dynamics and
Control. — Кyiv: Akademperiodyka, 2019. — 170 p. DOI: 10.15407/akademperiodyka.383.170. (Chapter 3)
[4] V.S. Aslanov, A.S. Ledkov, Attitude motion of cylindrical space debris during its removal by ion beam, Mathematical
Problems in Engineering. (2017) Article ID 1986374. DOI: 10.1155/2017/1986374.
6
7.
Задачи исследования• Исследовать особенности динамики
пассивного цилиндрического объекта
при его бесконтактной
транспортировке в плоском и
пространственном случае.
• Найти закон управления ионным
потоком, обеспечивающий
стабилизацию транспортируемого
объекта.
• Оценить выигрыш в затратах топлива
при управляемой транспортировке.
7
8.
Математическая модель. Плоское движениеДопущения
• Активный космический аппарат
рассматривается как
материальная точка
• Пассивный объект
рассматривается как цилиндр
• Учитывается влияние только
гравитационного поля Земли, сил
тяги и передаваемых ионным
потоком сил и моментов
8
9.
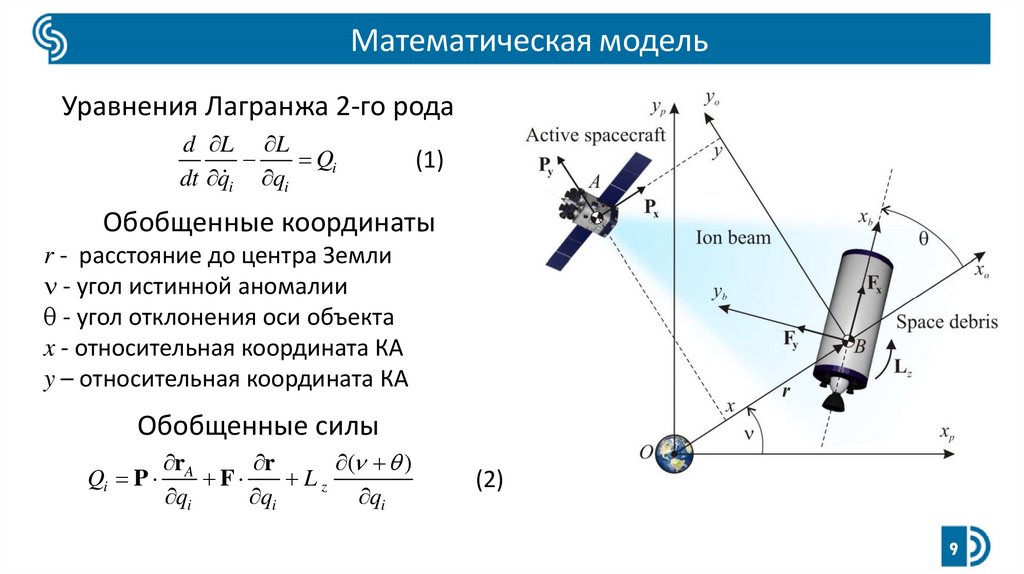
Математическая модельУравнения Лагранжа 2-го рода
d L L
Qi
dt qi qi
(1)
Обобщенные координаты
r - расстояние до центра Земли
- угол истинной аномалии
- угол отклонения оси объекта
x - относительная координата КА
y – относительная координата КА
Обобщенные силы
Qi P
rA
r
( )
F
Lz
qi
qi
qi
(2)
9
10.
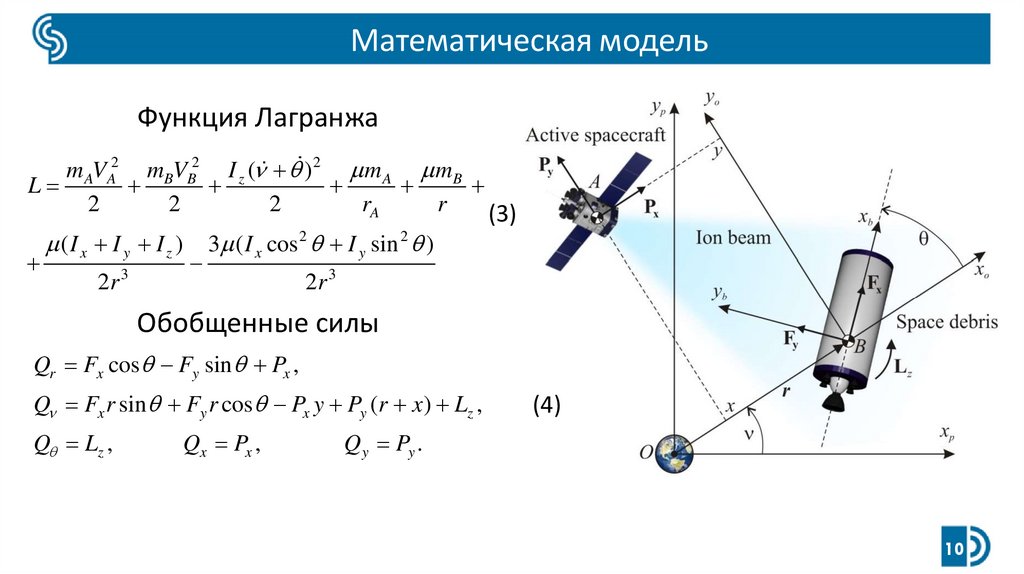
Математическая модельФункция Лагранжа
mAVA2 mBVB2 I z ( ) 2 m A mB
L
2
2
2
rA
r
(3)
( I x I y I z ) 3 ( I x cos 2 I y sin 2 )
3
2r
2r 3
Обобщенные силы
Qr Fx cos Fy sin Px ,
Q Fx r sin Fy r cos Px y Py (r x) Lz ,
Q Lz ,
Qx Px ,
(4)
Qy Py .
10
11.
Уравнения движенияr 2r
r
2
Fx cos Fy sin
mB
3 (3I x cos 2 3I y sin 2 I x I y I z )
2mB r
4
,
2 r Fx sin Fy cos 3 ( I x I y )sin cos
,
5
r
mB r
mB r
Lz 2 r Fx sin Fy cos 3 ( I x I y )sin cos 1
1
,
3
2
Iz
r
mB r
Iz
r
mB r
Px (r x)
2
x y r (r x) 2 y
,
3
mA
rA
y y (r x) 2 (r x)
2
Py
mA
y
rA3
(5)
.
11
12.
Упрощенная математическая модельДопущения: x=const, y=const, 1/r<<1
c r 2
r ( Fx sin Fy cos )
Lz 2cr 3 ( I x I y )sin cos
c 2 Fx cos Fy sin
r 3 2
, c
, 3
. (6)
3
mB
mB
Iz r
r r
Izr
Центр масс движется по Кеплеровой орбите
p
,
p c 2 1
1 e cos
Lz
p4
2e( 1)sin v 3( I x I y )sin 2
2
4
I z c (1 e cos v)
1 e cos v
2 I z (1 e cos v)
r
(7)
(8)
В случае малого эксцентриситета e<<1
Lz c 6 3( I x I y )sin 2
4 Lz c 6 cos v 3( I x I y )sin 2 cos v
e 2( 1)sin v
4
4
2I z
2I z
Iz
Iz
(9)
12
13.
Движение по орбите с малым эксцентриситетомA a0
4 Lz c 6 cos v 3( I x I y )sin 2 cos v
(a j cos j b j sin j ) B sin 2 e 2( 1)sin v
, (10)
4
2I z
Iz
j 1
k
Момент ионного потока
max
Lz Lz a0
6
3( I x I y )
Lmax
c
z
A
, B
4
2I z
Iz
(a j cos j b j sin j )
j 1
k
Невозмущенная система (e=0)
A a0
(a j cos j b j sin j ) B sin 2 0
j 1
k
3
2 Lmax
p
A
z
B 3 ( I x I y )
(11)
(12)
13
14.
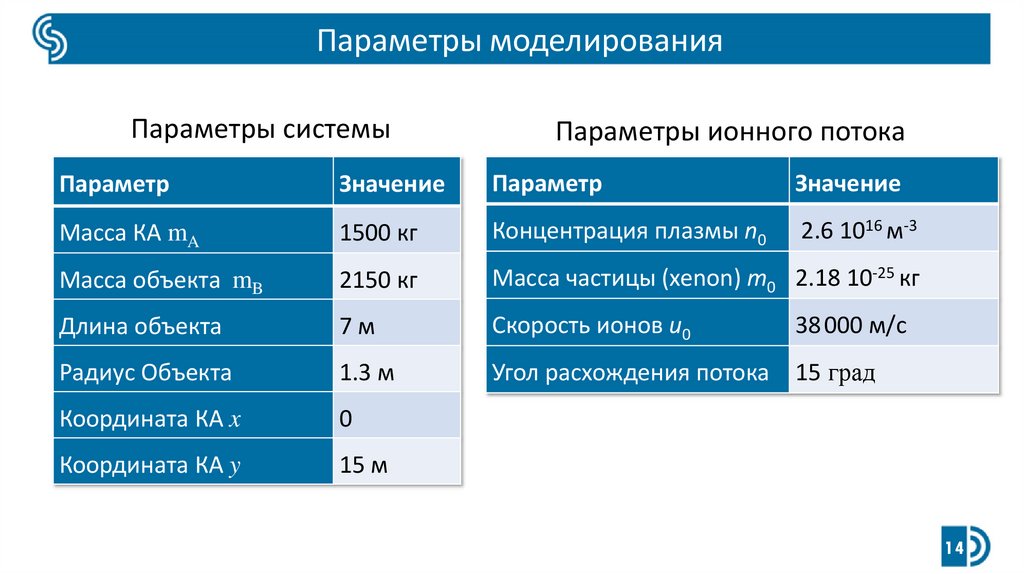
Параметры моделированияПараметры системы
Параметры ионного потока
Параметр
Значение
Параметр
Значение
Масса КА mA
1500 кг
Концентрация плазмы n0
2.6 1016 м-3
Масса объекта mB
2150 кг
Масса частицы (xenon) m0 2.18 10-25 кг
Длина объекта
7м
Скорость ионов u0
Радиус Объекта
1.3 м
Угол расхождения потока 15 град
Координата КА x
0
Координата КА y
15 м
38000 м/с
14
15.
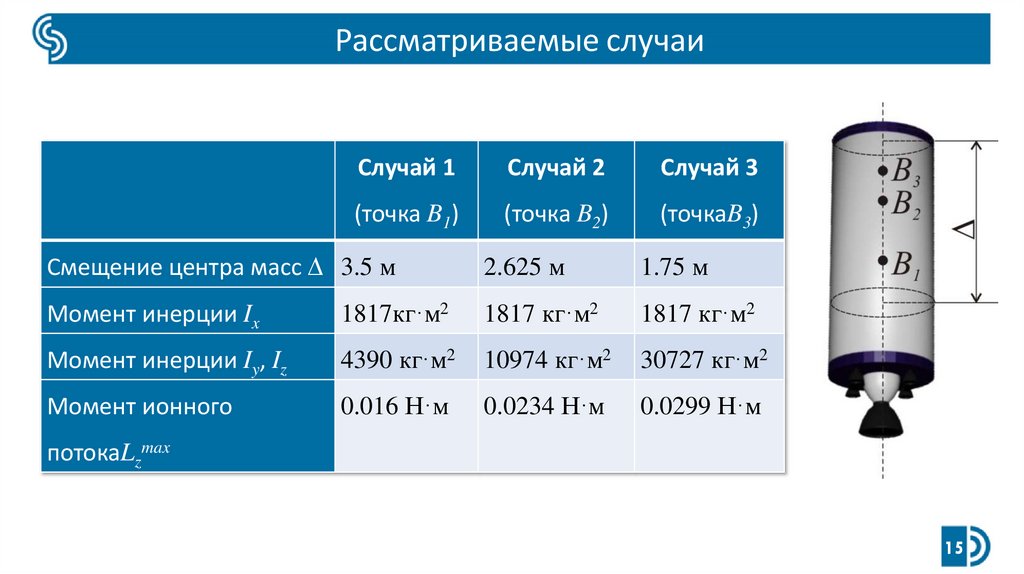
Рассматриваемые случаиСлучай 1
Случай 2
Случай 3
(точка B1)
(точка B2)
(точкаB3)
Смещение центра масс 3.5 м
2.625 м
1.75 м
Момент инерции Ix
1817кг·м2
1817 кг·м2
1817 кг·м2
Момент инерции Iy, Iz
4390 кг·м2
10974 кг·м2
30727 кг·м2
Момент ионного
0.016 Н·м
0.0234 Н·м
0.0299 Н·м
потокаLzmax
15
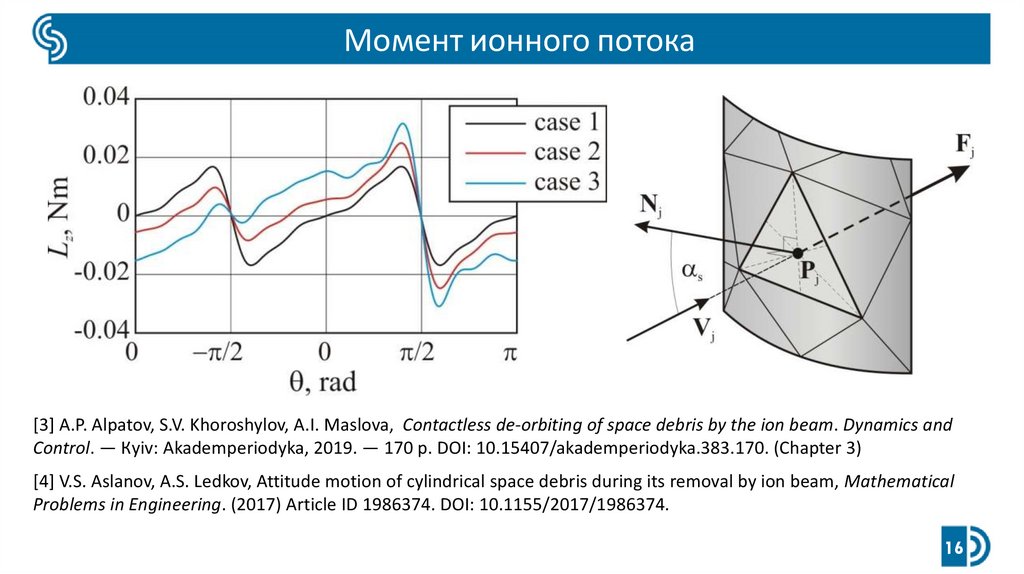
16.
Момент ионного потока[3] A.P. Alpatov, S.V. Khoroshylov, A.I. Maslova, Contactless de-orbiting of space debris by the ion beam. Dynamics and
Control. — Кyiv: Akademperiodyka, 2019. — 170 p. DOI: 10.15407/akademperiodyka.383.170. (Chapter 3)
[4] V.S. Aslanov, A.S. Ledkov, Attitude motion of cylindrical space debris during its removal by ion beam, Mathematical
Problems in Engineering. (2017) Article ID 1986374. DOI: 10.1155/2017/1986374.
16
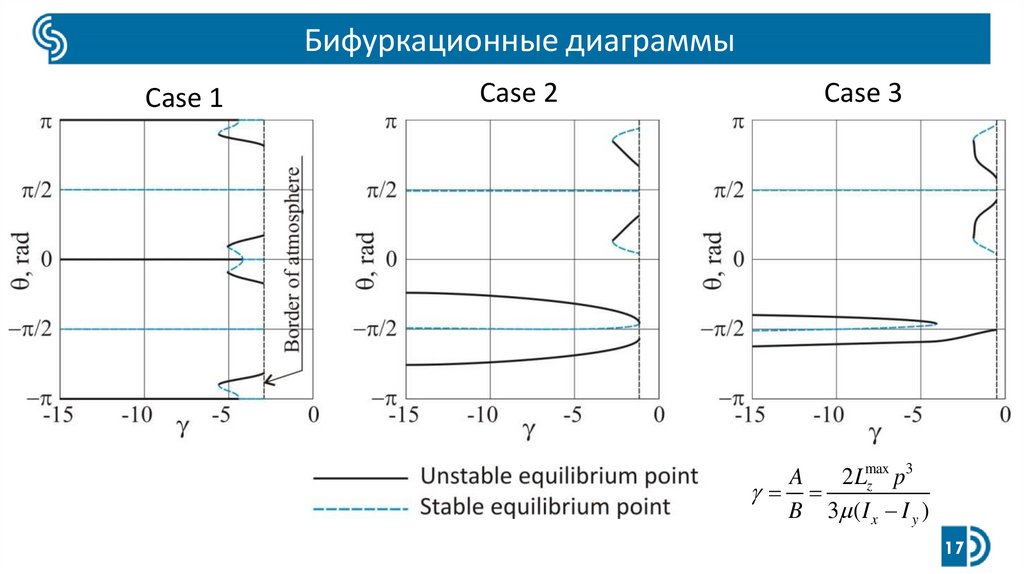
17.
Бифуркационные диаграммыCase 1
Case 2
Case 3
3
2 Lmax
p
A
z
B 3 ( I x I y )
17
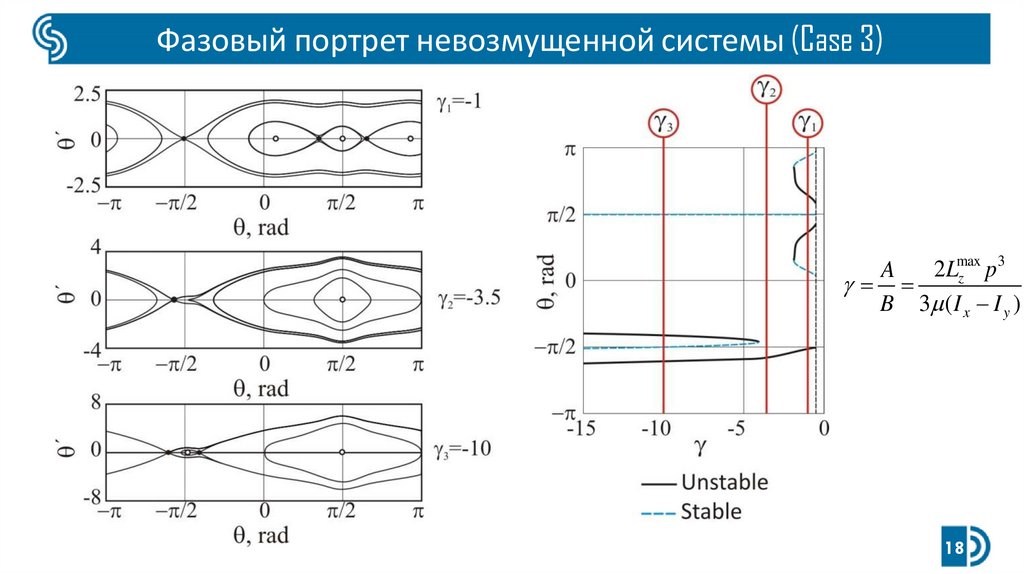
18.
Фазовый портрет невозмущенной системы (Case 3)3
2 Lmax
p
A
z
B 3 ( I x I y )
18
19.
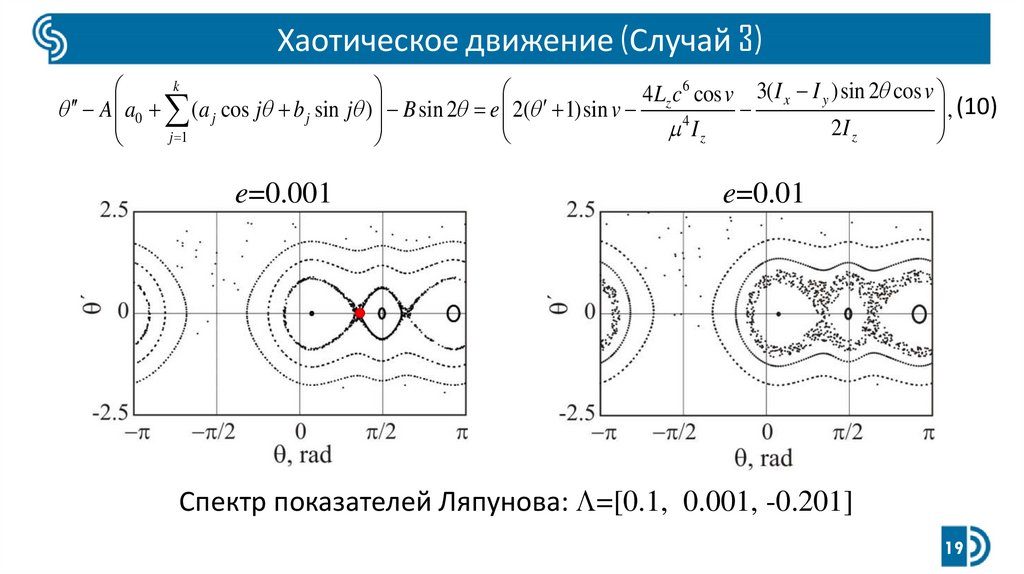
Хаотическое движение (Случай 3)A a0
4 Lz c 6 cos v 3( I x I y )sin 2 cos v
(a j cos j b j sin j ) B sin 2 e 2( 1)sin v
, (10)
4
2I z
Iz
j 1
k
e=0.001
e=0.01
Спектр показателей Ляпунова: =[0.1, 0.001, -0.201]
19
20.
Вывод• Топология фазового пространства может сильно изменяться в процессе
спуска. С увеличением эксцентриситета толщина хаотического слоя
увеличивается.
20
21.
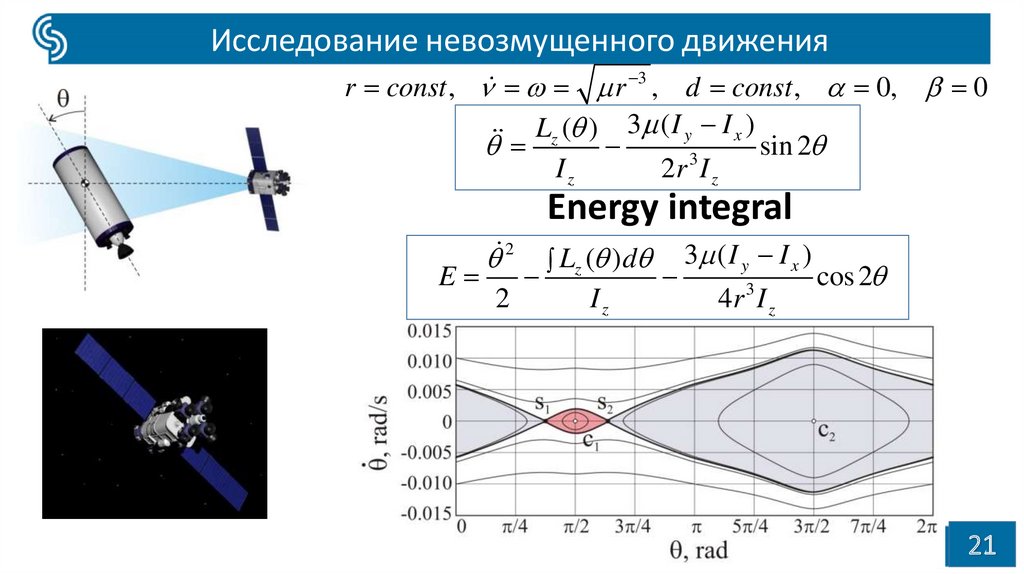
Исследование невозмущенного движенияr const , r 3 , d const , 0, 0
Lz ( ) 3 ( I y I x )
sin 2
3
Iz
2r I z
Energy integral
E
2
2
Lz ( ) d
Iz
3 ( I y I x )
3
4r I z
cos 2
21
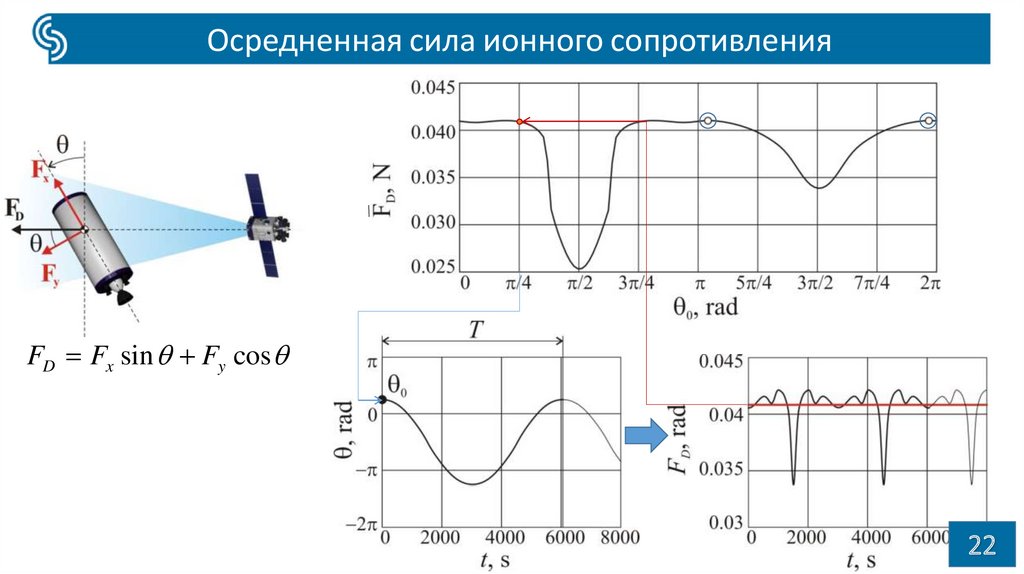
22.
Осредненная сила ионного сопротивленияFD Fx sin Fy cos
22
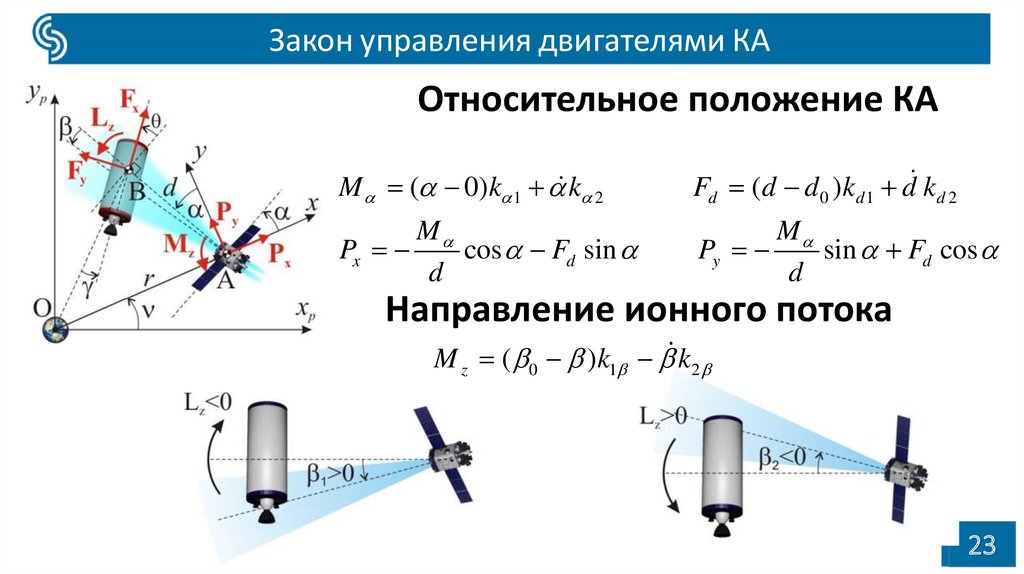
23.
Закон управления двигателями КАОтносительное положение КА
M ( 0) k 1 k 2
Fd (d d 0 )kd 1 d kd 2
M
Px
cos Fd sin
d
M
Py
sin Fd cos
d
Направление ионного потока
M z ( 0 )k1 k2
23
24.
Управление колебаниями объекта( 1 )k1 k2 , when Lz ( , 1 ) ( E* E ) 0,
M z ( 2 )k1 k2 , when Lz ( , 2 ) ( E* E ) 0,
k1 k2 otherwise
24
25.
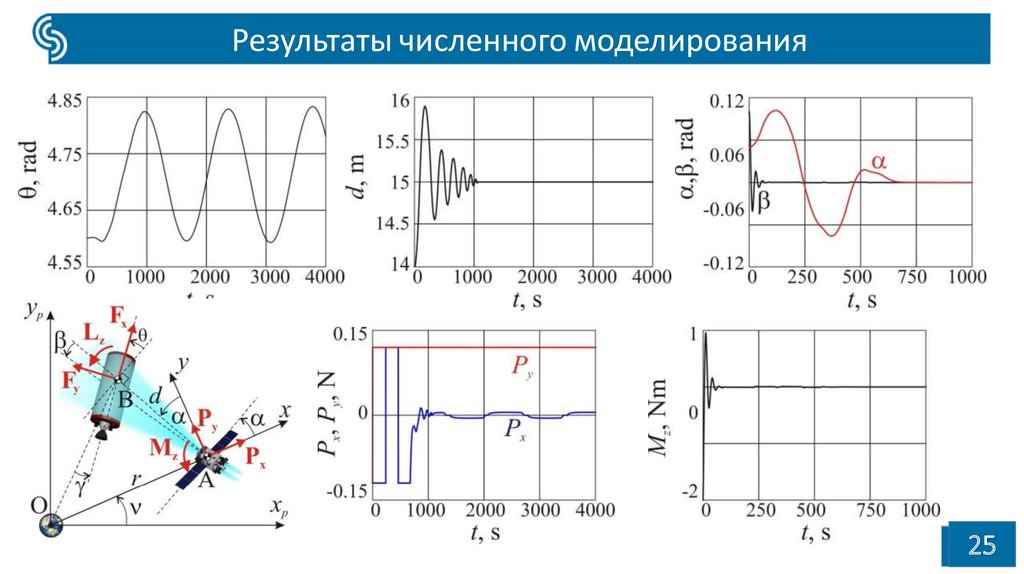
Результаты численного моделированияr0 7371000m, 0 r0 3 , d 0 14m, 0 0.05,
0 4.6, 0.1, r0 d 0 0 0 0 0 0
k 1 103 , k 2 5 104 , kd 1 200, kd 2 500, k1 20, k2 50
25
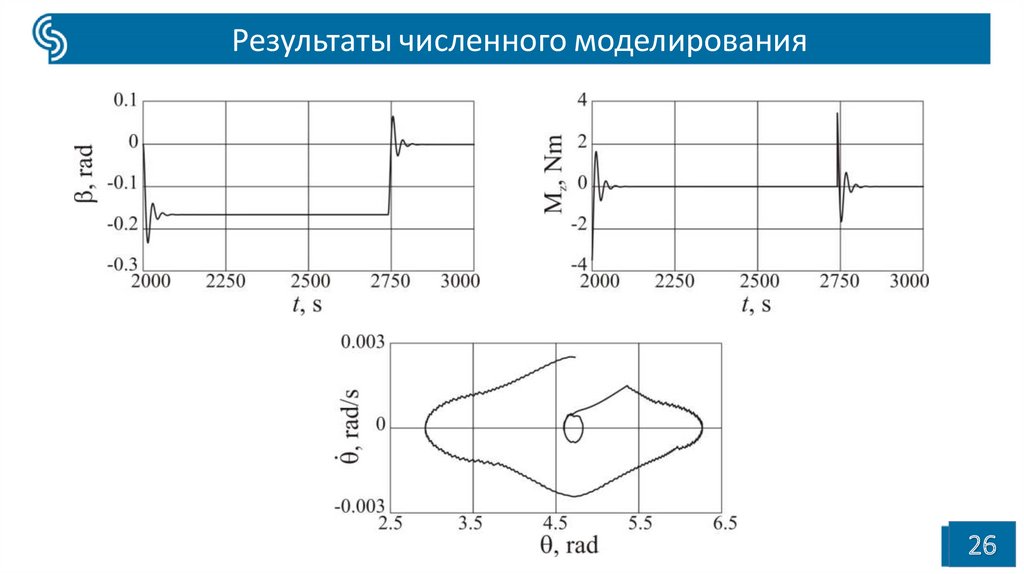
26.
Результаты численного моделирования26
27.
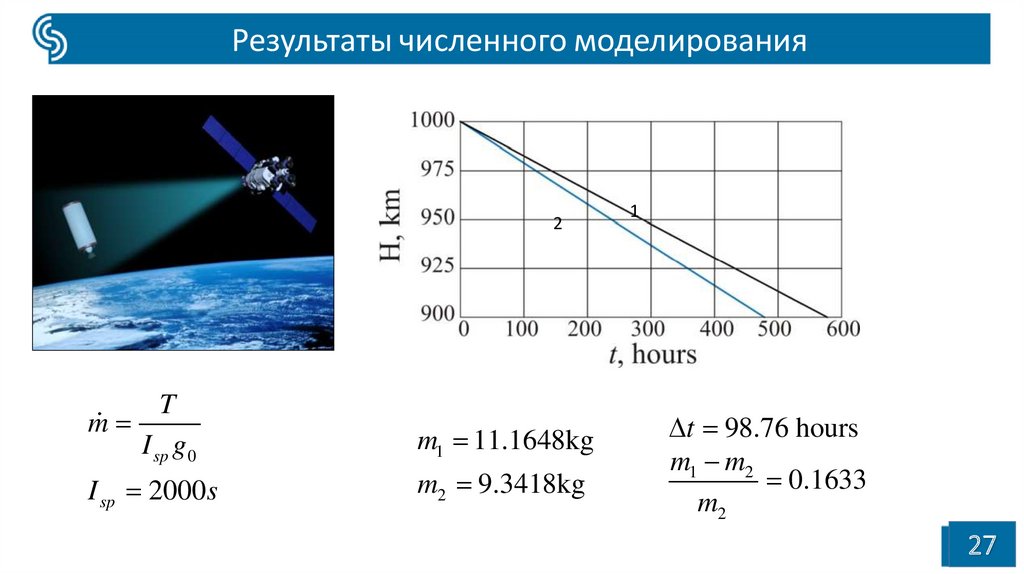
Результаты численного моделирования2
T
m
I sp g 0
I sp 2000 s
m1 11.1648kg
m2 9.3418kg
1
t 98.76 hours
m1 m2
0.1633
m2
27
28.
Вывод• Управление угловым движением объекта при
его транспортировке позволяет существенно
снизить затраты топлива
• Даже без приема во внимание влияния
угловых колебаний объекта,
рассматриваемая технология позволяет
решать задачу бесконтактной
транспортировки
28
29.
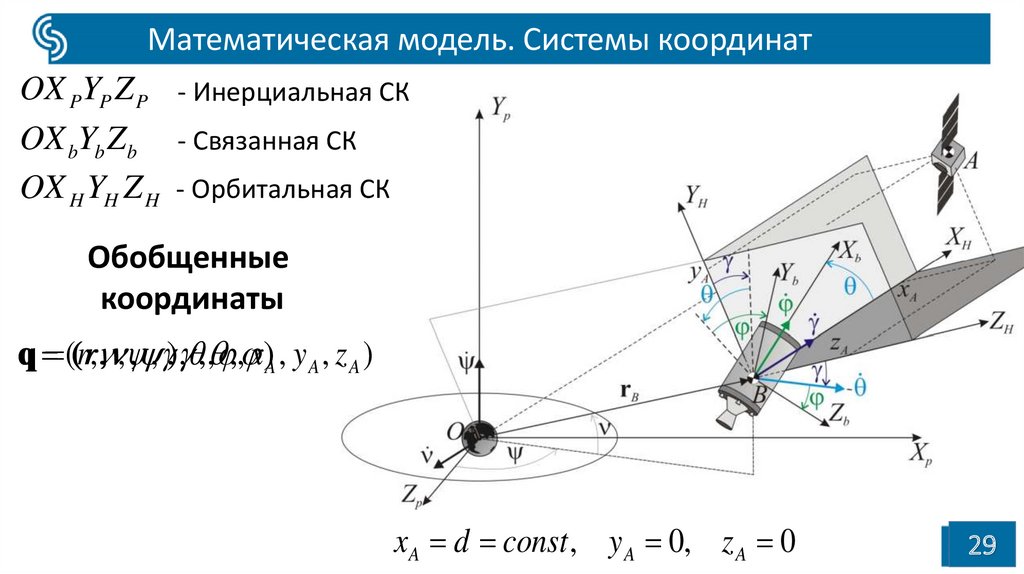
Математическая модель. Системы координатOX PYP Z P - Инерциальная СК
OX bYb Z b - Связанная СК
OX H YH Z H - Орбитальная СК
Обобщенные
координаты
q ((rr, , , , , ), , ,, ,, x)A , y A , z A )
x A d const , y A 0, z A 0
29
30.
Движение центра массmB r G F
p
p
B
p
I
(1)
G Bp mB r p r 3
Гравитационная сила
FiH [ FixH , FiyH , FizH ]T Ионная сила
Уравнения движения
H
Fiz
2
2
2
r r ( cos v ) 2
, (2)
r
mB
FixH
2 sin v 2 r
, (3)
c cos v
r
rmB cos v
H
2 r Fiy
2
sin v cos v
. (4)
r
rmB
30
31.
Движение относительно центра массdH bB
(5)
ωb H bB LbG LbI
dt
b
b
Момент количества движения
H B [I ]ω
[I ]
Тензор инерции
ωb [ x , y , z ]T
Угловая скорость
3 b
b
LG 5 r [I ]r b Гравитационный момент
r
LbI [ LIx , LIy , LIz ]T Ионный момент
ω ν ψ γ θ φ
b
b
b
b
b
b
(6)
31
32.
Рассмотрим движение на GEOR I x x , G R cos ( z sin y cos )sin
Ix Ix / I,
Iy Iz I
Iz
(G R cos )( R G cos ) L ( )
3
sin
I
R L Ix ( ) I 1
1
1
G LIx ( ) I cos LIy ( ) I sin
2
(G R cos )sin
1
2
RI x (G R cos ) cos sin
Ix
L LIx ,
Iz
(7)
(8)
(9)
(10)
(11)
(12)
Iy
L LIy cos LIz sin ,
L LIy sin LIz cos
32
33.
Уравнения движения ЦМ на GEOLIx LIy 0,
u [0,1]
max k
I
j
LIz uL
b j sin j
Control parameter
k
(G R cos )( R G cos ) uLmax
I
b j sin j
3
sin
I j
R const , G const
2
W ( ) E
2
G R 2GR cos uL
W ( )
2
2sin
I
2
2
max
k
I
bj
j
j
(13)
(14)
(15)
cos j (16)
33
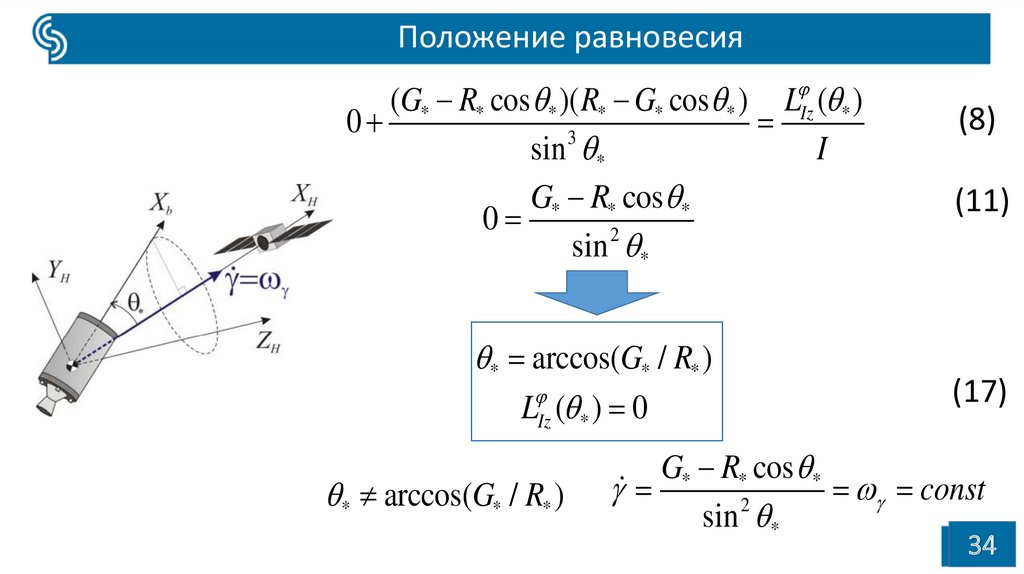
34.
Положение равновесия* Iz
Iz
(G* RRcos
G* cos
)(*R)( R
*G cos
) L) ( L) ( * )
* cos
0
3 3
sinsin *
I I
G* RRcos
* cos *
0
22
sin
sin *
* arccos(G* / R* )
LIz ( * ) 0
* arccos(G* / R* )
(8)
(11)
(17)
G* R* cos *
const
2
sin *
34
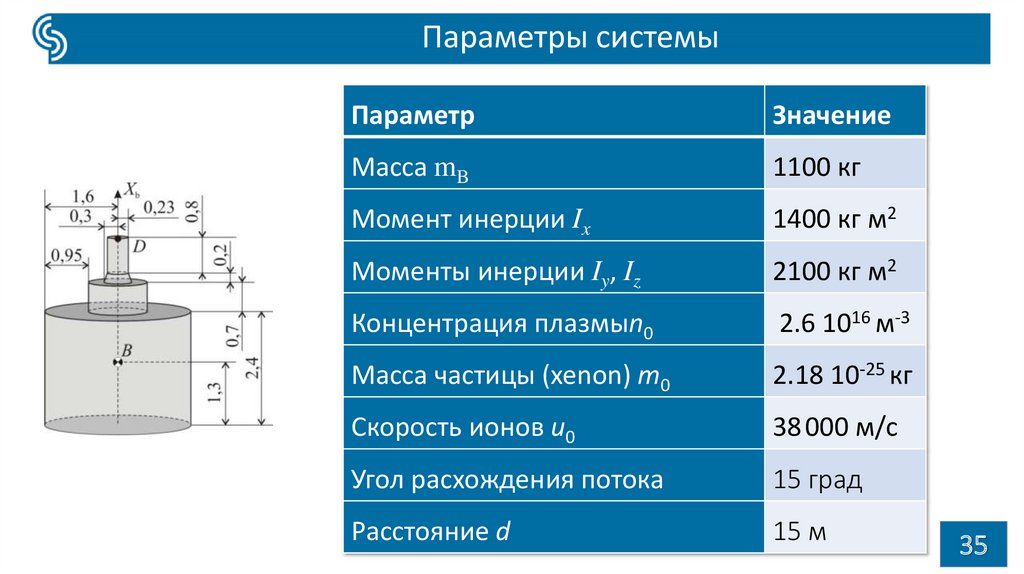
35.
Параметры системыПараметр
Значение
Масса mB
1100 кг
Момент инерции Ix
1400 кг м2
Моменты инерции Iy, Iz
2100 кг м2
Концентрация плазмыn0
2.6 1016 м-3
Масса частицы (xenon) m0
2.18 10-25 кг
Скорость ионов u0
38 000 м/с
Угол расхождения потока
15 град
Расстояние d
15 м
35
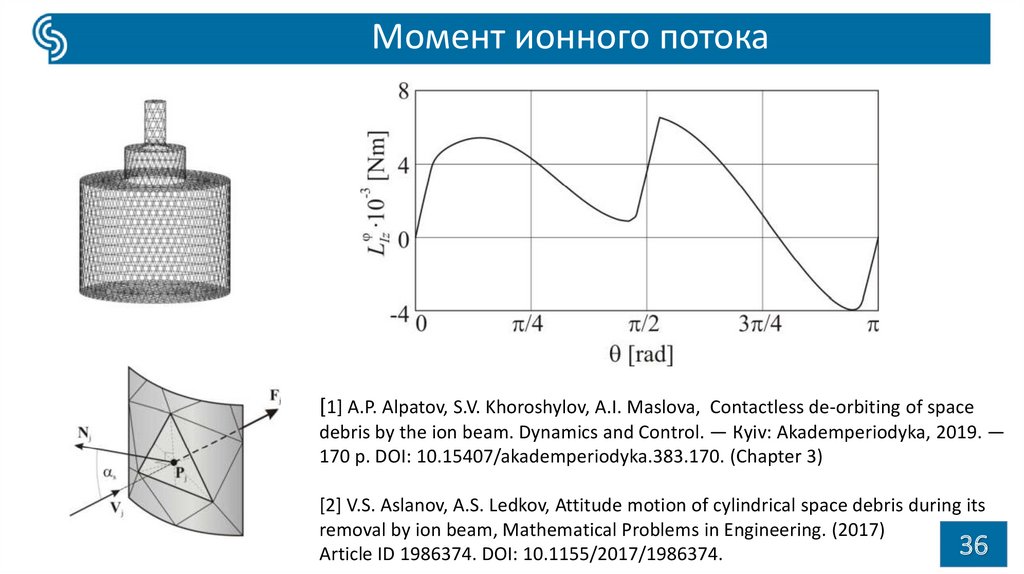
36.
Момент ионного потока[1] A.P. Alpatov, S.V. Khoroshylov, A.I. Maslova, Contactless de-orbiting of space
debris by the ion beam. Dynamics and Control. — Кyiv: Akademperiodyka, 2019. —
170 p. DOI: 10.15407/akademperiodyka.383.170. (Chapter 3)
[2] V.S. Aslanov, A.S. Ledkov, Attitude motion of cylindrical space debris during its
removal by ion beam, Mathematical Problems in Engineering. (2017)
36
Article ID 1986374. DOI: 10.1155/2017/1986374.
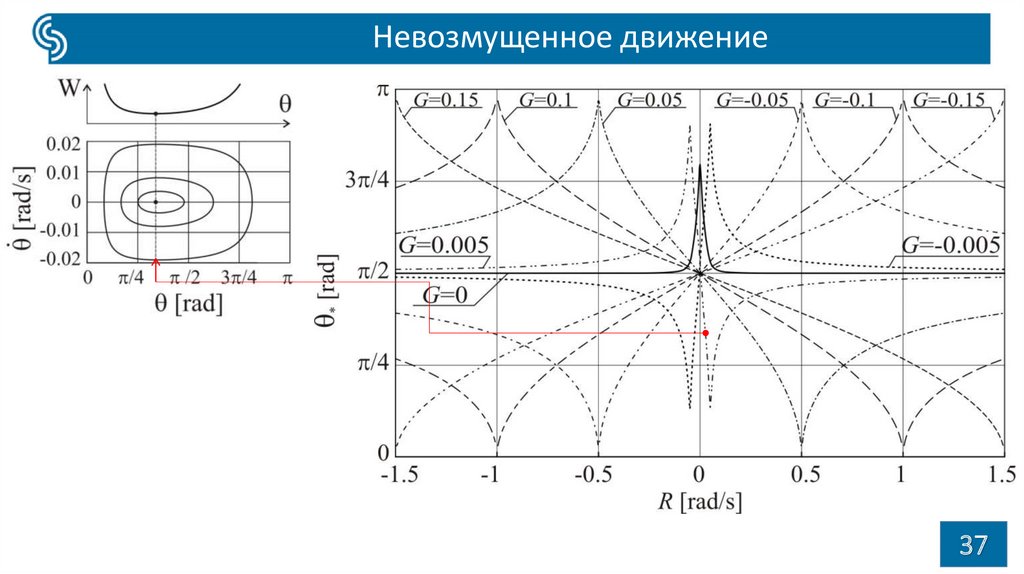
37.
Невозмущенное движение37
38.
Закон управления тягой ионного двигателяmax k
I
j
LIz uL
b j sin j
1 k ( * ) [( * ) ], when k ( * ) 1;
u
when k ( * ) 1;
1,
Функция Хевисайда
H []
1
k
max(| ( * ) |)
Закон управления
[ t T ,t ]
38
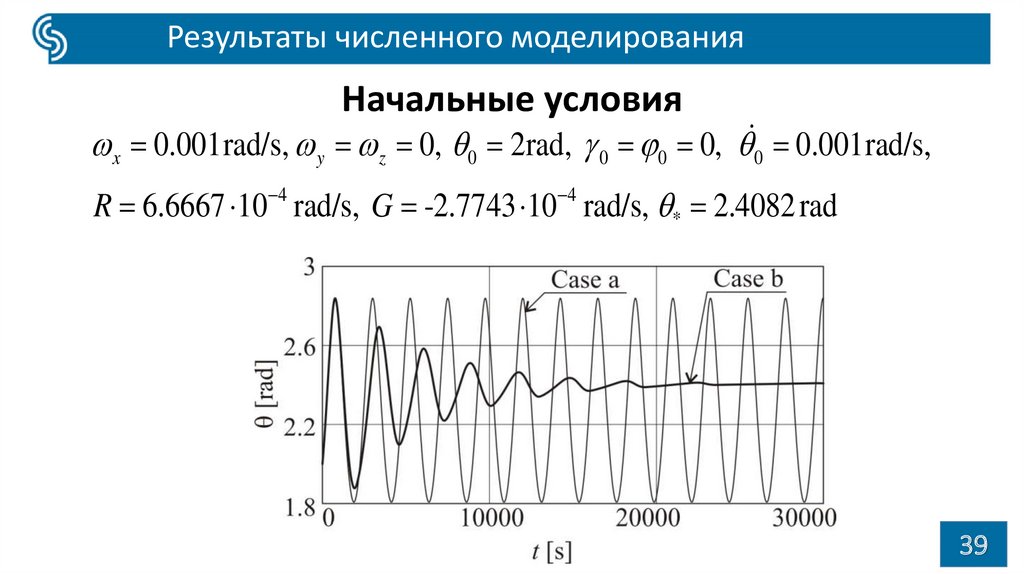
39.
Результаты численного моделированияНачальные условия
x 0.001rad/s, y z 0, 0 2rad, 0 0 0, 0 0.001rad/s,
R 6.6667 10 4 rad/s, G -2.7743 10 4 rad/s, * 2.4082 rad
39
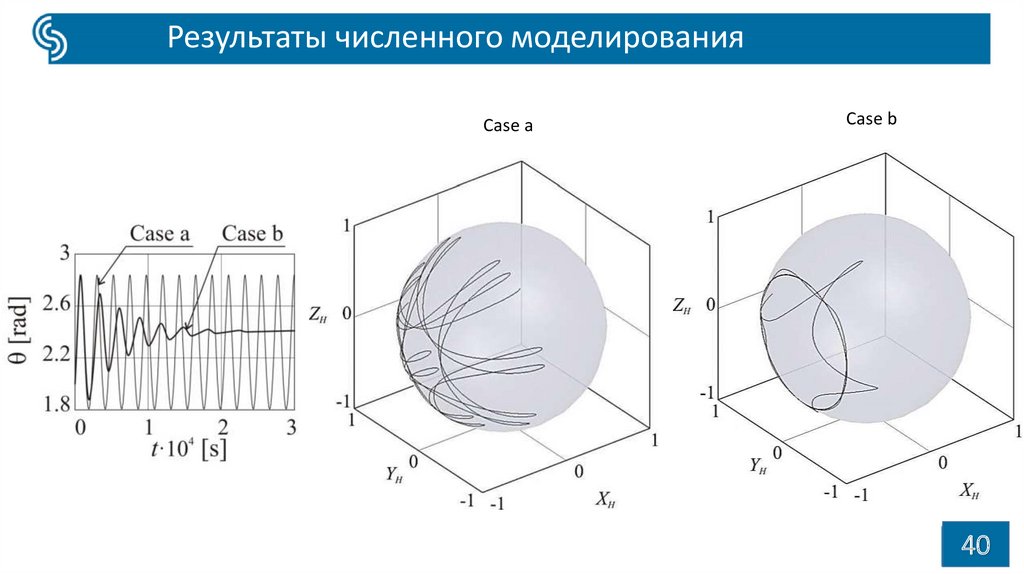
40.
Результаты численного моделированияCase a
Case b
40
41.
Результаты и выводы• Исследовано невозмущенное
движение системы
• Предложен закон управления тягой
ионного двигателя.
• Эффективность закона подтверждаете
результатами численного
моделирования.
41
42.
Спасибо за вниманиеВ.С. Асланов
URL: aslanov.ssau.ru
Email:aslanov_vs@mail.ru
А.С. Ледков
URL: ledkov.com
Email:ledkov@inbox.ru




















 physics
physics








