Основные определения динамики. Лекция 1

1.

Динамика – часть теоретической механики, изучающая движение
материальных объектов в зависимости от сил, вызвавших это движение
Основные положения динамики и аксиомы впервые выдвинуты Ньютоном и Галилеем в XVII веке.
Основные положения динамики сформулированы применительно к материальной точке.
В основе классической динамики лежат два основных допущения:
1. Существование абсолютного пространства:
пространство обладает чисто геометрическими свойствами, не зависящими от материи
и ее движения.
2. Абсолютное время:
время считается независимым.
На основании этих допущений утверждается:
1. Существование абсолютно неподвижной системы отсчета:
2. Независимость изменения времени от движения системы отсчета:
В большинстве задач динамики массы движущихся материальных точек не зависят от
скоростей движения и остаются постоянными при всех обстоятельствах, обусловливающих
движение.

2.

1-й закон Ньютона
Изолированная материальная точка (не подверженная воздействию
других объектов) относительно неподвижной системе отсчета
движется равномерно и прямолинейно ( v = const ) или находится в
покое ( v = 0 )
Такое кинематическое состояние точки называется инерциальным.
Инерциальное кинематическое состояние точки определяется равенством нулю ее ускорения a = 0.
Система отсчета, движущаяся поступательно, равномерно и прямолинейно называется
инерциальной.
Аксиома применима и к инерциальным системам отсчета.

3.

2-й закон Ньютона
Ускорение, сообщаемое материальной точке относительно инерциальной
системы отсчета, прямо пропорционально силе, действующей на точку, и
обратно пропорционально массе этой точки
F ma
a
F
Массой называется физическая характеристика и мера инерционных свойств вещества.
В поле силы тяжести Земли масса может быть определена по формуле:
P
m
g
(P – сила тяжести, g – ускорение свободного падения)
Масса является также мерой и характеристикой гравитационных свойств вещества.

4.

3-й закон Ньютона
Две материальные точки взаимодействуют с силами, одинаковыми по
модулю и действующими по одной прямой, соединяющей точки, в
противоположные стороны
М1
F1
F2
F1 F2
F1 F2
М2

5.

Принцип суперпозиции
Материальная точка, под действием нескольких сил приобретает
ускорение, равное векторной сумме тех ускорений, которые она бы
получила от каждой силы, действующей независимо от других
F3
a3
an
М
an
Fn
a2
a
a1
a a1 a2 a3 ... an
F2 ma F ; ma F ; ma3 F3 ; man Fn ;
1
1
2
2
a3
ma ma1 ma2 ma3 ... man
ma F1 F2 F3 ...F4 ;
a2 F
1
ma Fi
n
i 1

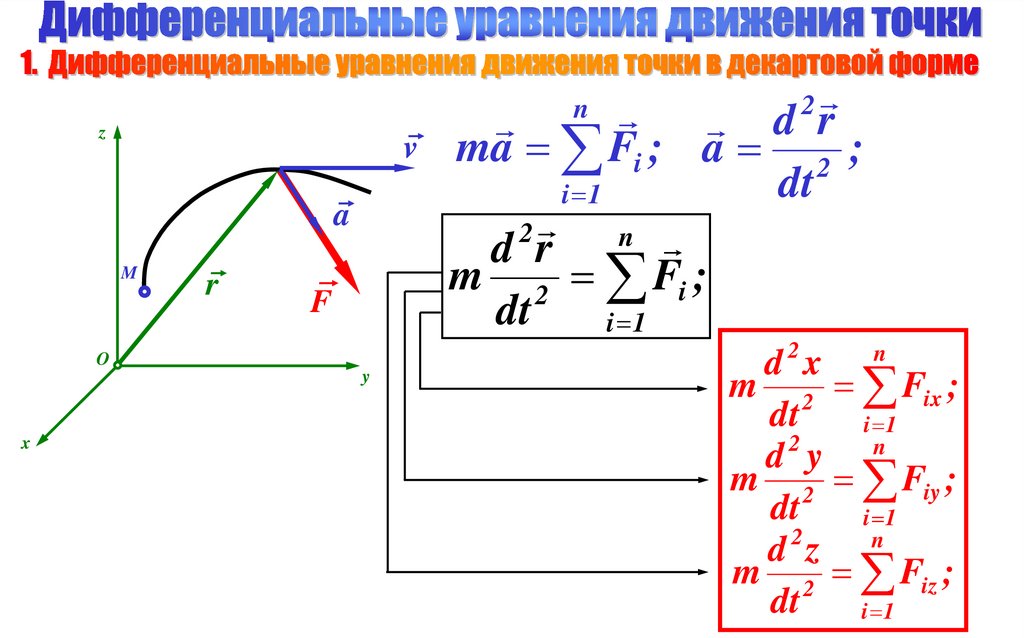
6.

d r
ma Fi ; a 2 ;
dt
i 1
2
n
d r
m 2 Fi ;
dt
i 1
2
n
z
v
a
M
r
F
2
O
y
x
d x n
m 2 Fix ;
dt
i 1
2
n
d y
m 2 Fiy ;
dt
i 1
2
n
d z
m 2 Fiz ;
dt
i 1

7.

b
v τ
S
a
ma Fi
n
i 1
n
n
M
n
F
dv
dv
ma Fi ; a ; m Fi ;
dt i 1
dt
i 1
2
2
n
n
v
v
man Fin ; an ; m Fin ;
i 1
n
mab Fib ; ab 0 ;
i 1
i 1
n
0 Fib ;
i 1

8.

Зная массу точки и закон ее движения
определить действующую на точку силу.
x f1 ( t ); y f2 ( t ); z f3 ( t );
Уравнения движения точки:
Скорость точки:
dy df2
dz df3
dx df1
; vz
;
vx
; vy
dt dt
dt dt
dt dt
2
2
Ускорение точки:
dv y d y
dvz d z
dvx d x
2 ; az
2;
ax
2 ; ay
dt
dt dt
dt
dt
dt
2
Сила:
2
2
2
d y
d z
d x
Fx ma x m 2 ; Fy ma y m 2 ; Fz ma z m 2 ;
dt
dt
dt

9.

По заданной массе и действующей на
точку силе определить движение точки.
Сила: Fx Fx ( t , x , y , z , x , y , z ); Fy Fy ( t , x , y , z , x , y , z ); Fz Fz ( t , x , y , z , x , y , z );
t
dvx
vx
t
Скорость точки: m
Fx ; m dv x Fx dt ; m v x v x 0 x , где x Fx dt ;
t0
vx0
t0
dt
dv y
v
t
t
m
Fy ; m y dv y Fy dt ; m v y v y0 y , где y Fy dt ;
v y0
t0
t0
dt
dvz
t
vz
t
m
Fz ; m dvz Fz dt ; m vz vz 0 y , где y Fy dt ;
t0
vz 0
t0
dt
Уравнения движения точки:
x
t
t
dx
1
mv x x mv x 0 , m x mv x 0 , mdx x mv x 0 dt , m x dx t x dt t mv x 0 dt , x x v x 0 t x0 ,
0
0
0
dt
m
t
где x x dt ;
t0
y
t
t
dy
1
mv y y mv y0 , m y mv y0 , mdy y mv y0 dt , m dy y dt mv y0 dt , y y v y0 t y0 ,
y0
t0
t0
dt
m
t
где y y dt ;
t0
z
t
t
dz
1
mv z z mv z 0 , m z mv z 0 , mdz z mv z 0 dt , m z dx t z dt t mv z 0 dt , z z vz 0 t z0 ,
0
0
0
dt
m
t
где z z dt ;
t0

10.

Сила зависит от времени: F F ( t ); Метод разделения переменных
v
t
t
dv
1
m F t ; m dv F ( t )dt ; m v dv t F ( t )dt ; m v v0 t , где t t F t dt ; v t v0 ;
0
0
0
dt
m
s
t
1 t
ds 1
1
1
t v0 , ds ( t ) v x 0 dt , s ds t t dt t v0 dt , s t v0 t s0 ,
0
0
m 0
dt m
m
m
Сила зависит от скорости: F F ( v ); Метод разделения переменных
v dv
t
dv
dv
dv
m
dt
;
m
v
v
t
t
,
где
v
; v0 const ;
m
dt
;
m F v ;
0
0
v
t
0 F v
0
F v
F( v )
dt
Сила зависит от перемещения: F F ( s ); Метод замены переменных
v
s
dv
v dv
dv ds
m F s ; m F ( s ); m
F ( s ); m vdv F ( s )ds ; m vdv F ( s )dt ;
v0
s0
dt
ds
dt ds
s
2
mv 2 mv02
s v02 ;
s , где s F s ds ; v
s0
m
2
2

11.

Точка, имеющая массу m, движется в плоскости xOy согласно уравнениям
x = a·cos(kt);
y = b ·sin(kt), где a, b, k – постоянные, t – время.
Найти силу, под действием которой точка совершает это движение.
y
Решение: Уравнение траектории:
r
O
x(t)
F
y( t )
x
x a cos kt
y b sin kt
2
2
2
Эллипс
2
x
y
2
2
cos kt sin kt ;
a
b
d2x
Fx m 2 mk 2 a cos kt mk 2 x
dt
2
d y
2
2
Fy m 2 mk b sin kt mk y
dt
Ответ:
2
2
x
y
1
a
b
r x y
2
2
F Fx2 Fy2 mk 2 x 2 y 2 mk 2 r ;
cos F , x Fx F x r ;
cos F , y Fy F y r .
F mk r
2

12.

Точка, имеющая массу m, брошена с поверхности земли со скоростью v0 под
углом α к горизонту в вертикальной плоскости. Сила сопротивления воздуха
направлена против движения и пропорциональна скорости и массе R = kmv.
Найти уравнения движения точки.
Решение: Дифференциальные уравнения движения точки:
y
R
v0
y( t )
α
O
v
x(t)
2
mg
d x
m 2 mkv x ;
dt
2
d y
m 2 mg mkv y ;
dt
ma P R
d2x
m 2 Rx ;
dt
d2 y
m 2 mg Ry ;
dt
x
Понижение порядка дифуравнений:
dx
vx
;
dt
dy
vy ;
dt
dvx
m
mkv x ;
dt
dv y
m
mg mkv y ;
dt
Начальные условия:
При t = 0:
x0 = 0; y0 = 0;
vx0 = v0cosα;
vy0 = v0sinα;

13.

Точка, имеющая массу m, брошена с поверхности земли со скоростью v0 под
углом α к горизонту в вертикальной плоскости. Сила сопротивления воздуха
направлена против движения и пропорциональна скорости и массе R = kmv.
Найти уравнения движения точки.
Решение:
Разделение
переменных:
Интегрирование:
dvx
dt ;
kvx
dv y
dt ;
g kv y
Определение
произвольных
постоянных:
Результат:
dvx
kv dt ;
x
dv y
g kv dt ;
y
C1 v0 cos ;
g
C 2 v0 sin ;
k
ln v x kt ln C1 ;
v x C1e kt ;
g
g
ln v y kt ln C2 ; v y C 2 e kt ;
k
k
Окончательный
результат первого
интегрирования:
v x v0 cos e kt ;
g g
kt
v y v0 sin e ;
k k

14.

Точка, имеющая массу m, брошена с поверхности земли со скоростью v0 под
углом α к горизонту в вертикальной плоскости. Сила сопротивления воздуха
направлена против движения и пропорциональна скорости и массе R = kmv.
Найти уравнения движения точки.
Решение:
Разделение переменных:
dx
kt
kt
v0 cos e ;
dx v0 cos e dt ;
dt
dy
g g
g g
kt
kt
v0 sin e ; dy v0 sin e dt ;
dt
k k
k k
Интегрирование:
dx v0 cos e
kt
dt ;
g
g
kt
dy k dt k v0 sin e dt ;
1
x v0 cos e kt C 3 ;
k
g
1 g
kt
y t v0 sin e C4 ;
k
k k

15.

Точка, имеющая массу m, брошена с поверхности земли со скоростью v0 под
углом α к горизонту в вертикальной плоскости. Сила сопротивления воздуха
направлена против движения и пропорциональна скорости и массе R = kmv.
Найти уравнения движения точки.
Решение:
Определение произвольных
постоянных:
Окончательный результат второго
интегрирования:
Ответ:
1
kt
x v0 cos 1 e ;
k
1
C 3 v0 cos ;
k
1 g
C4 v0 sin ;
k k
1 g
g
kt
y v0 sin 1 e t .
k k
k
1 g
g
1
kt
kt
x v0 cos 1 e , y v0 sin 1 e t .
k
k k
k