Similar presentations:
Собственные функции
1.
Собственные функции1. «Игрушечная» задача. Найти собственные функции оператора чётности
Уравнение на собственные значения
Iˆ I x I I x
Собственные функции?
2.
Собственные функцииСобственные значения
I 1
Уравнение на собственные значения
Iˆ I x I I x I x
Но
Iˆ I x I x I x
Собственные функции – чётные и нечётные функции аргумента
I 1, I x I x ; I 1, I x I x
3.
Оператор координатыПостулат: среднее значение оператора физической величины fˆ в состоянии, описываемом
волновой функцией x , определяется равенством
f dx * x fˆ x
Среднее значение координаты
x dx x x dx * x x x dx * x xˆ x
Оператор координаты в координатном представлении
x̂ x x x
Является ли оператор координаты эрмитовым?
Задача. Волновая функция частицы определяется равенством
p0 x x 2
x C exp i
2
2a
Вычислить
x , x x , p, p p
2
2
4.
Задача: найти собственные значения и собственные функции оператораfˆ pˆ xˆ, * , *
Надо решить уравнение
pˆ xˆ f x f f x
Собственные функции должны быть ограниченными
f x M , M M * , x ] , [
5.
Явный вид уравненияd
x
i dx
f x f f x
Или
d f x
f x
i
f x dx
Решение
i
x2
f x C f exp
fx
2
Какие ограничения необходимо наложить на f ?
6.
Ограничение на собственные заченияf f*
Воспользовавшись условиями ортогональности
*
dx
f x f x f f
полноты
*
df
f x f x x x
и свойствами дельта-функции, найти нормировочный коэффициент
Cf ?
7.
Условие ортогональностиi
dx
x
x
C
C
dx
exp
f
f
x
f
f
f f
f
*
f
Или
2 C f f f f f
2
Cf
1
2
Так как волновая функция определена с точностью до фазового множителя, то
Cf
1
2
8.
Условие полноты*
df
f x f x C f
2
i
i
exp
x 2 x 2 df exp
f x x x x
2
Свойство дельта-функции
f x, x x x f x, x x x f x , x x x
Тогда
2 C f
2
x x x x
Cf
1
2
Так как волновая функция определена с точностью до фазового множителя, то
Cf
1
2
Ответ
i
x2
f x
exp
fx
2
2
1
9.
Собственные функции оператора импульсаВоспользовавшись результатами предыдущей задачи, найти собственные функции
оператора импульса?
10.
Собственные функции оператора импульсаfˆ pˆ xˆ 1, 0 pˆ
Тогда
eipx /
p x
2
11.
Собственные функции оператора координатыКазалось бы, что можно воспользоваться результатами предыдущей задачи
fˆ pˆ xˆ 0, 1 xˆ
но возникает неопределённость
i
x2
f x
exp
fx
2
2
1
Поэтому решим уравнение на собственные значения непосредственно для оператора
координаты!
12.
Уравнение на собственные значенияxˆ x0 x x0 x0 x
Или
x x0 x x0 x0 x
x x0 x x 0
0
Плюс условия ортогональности и полноты
*
dx
x0 x x0 x x0 x0
*
dx
0 x0 x x0 x x x
x0 x ?
13.
Ответx0 x x x0
14.
Трудности интерпретации физического смысла собственных значений оператора снепрерывным спектром (на примере оператора импульса).
Постулат: волновая функция, описывающая состояние физической системы
ДОЛЖНА быть квадратично интегрируема!












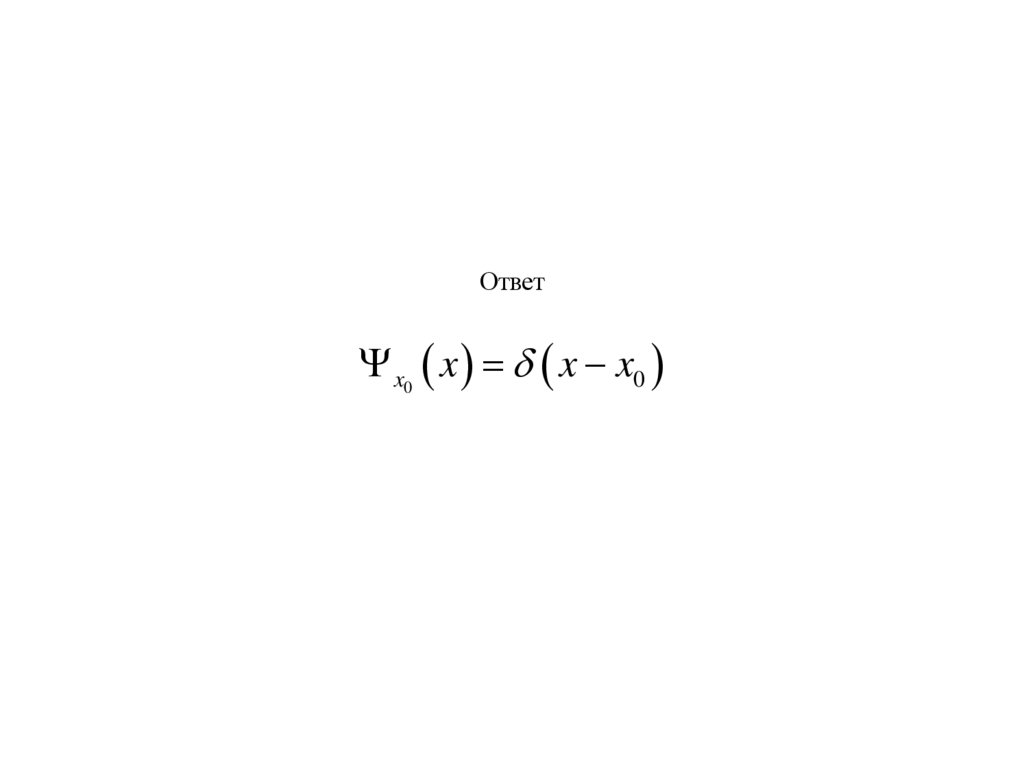

 mathematics
mathematics








