Similar presentations:
Конус
1.
Конус.2.
Определение.Конус – тело, полученное объединением всех
лучей, исходящих из одной точки
(вершины конуса) и проходящих через плоскую
поверхность.
Круглый конус может быть получен вращением
прямоугольного треугольника вокруг одного из
его катетов.
3.
Свойства.Если площадь основания конечна, то объём конуса также конечен и равен
трети произведения высоты на площадь основания.
где S — площадь основания, H — высота. Таким образом, все конусы,
опирающиеся на данное основание (конечной площади) и имеющие
вершину, находящуюся на данной плоскости, параллельной основанию,
имеют равный объём, поскольку их высоты равны.
Центр тяжести любого конуса с конечным объёмом лежит на четверти
высоты от основания.
Телесный угол при вершине прямого кругового конуса равен
где α — угол раствора конуса.
4.
Площадь боковой поверхности такого конусаравна
а полная площадь поверхности (т. е. сумма
площадей боковой поверхности и основания)
где R — радиус основания, l — длина образующей.
Объём кругового конуса равен
Для усечённого конуса (не обязательно прямого и
кругового) объём равен:
где S1 и S2 — площади соответственно верхнего
(ближнего к вершине) и нижнего
оснований, h и H — расстояния от плоскости
соответственно верхнего и нижнего основания до
вершины.
Пересечение плоскости с прямым круговым
конусом является одним из конических
сечений (в невырожденных случаях —
эллипсом, параболой илигиперболой, в
зависимости от положения секущей плоскости).
5.
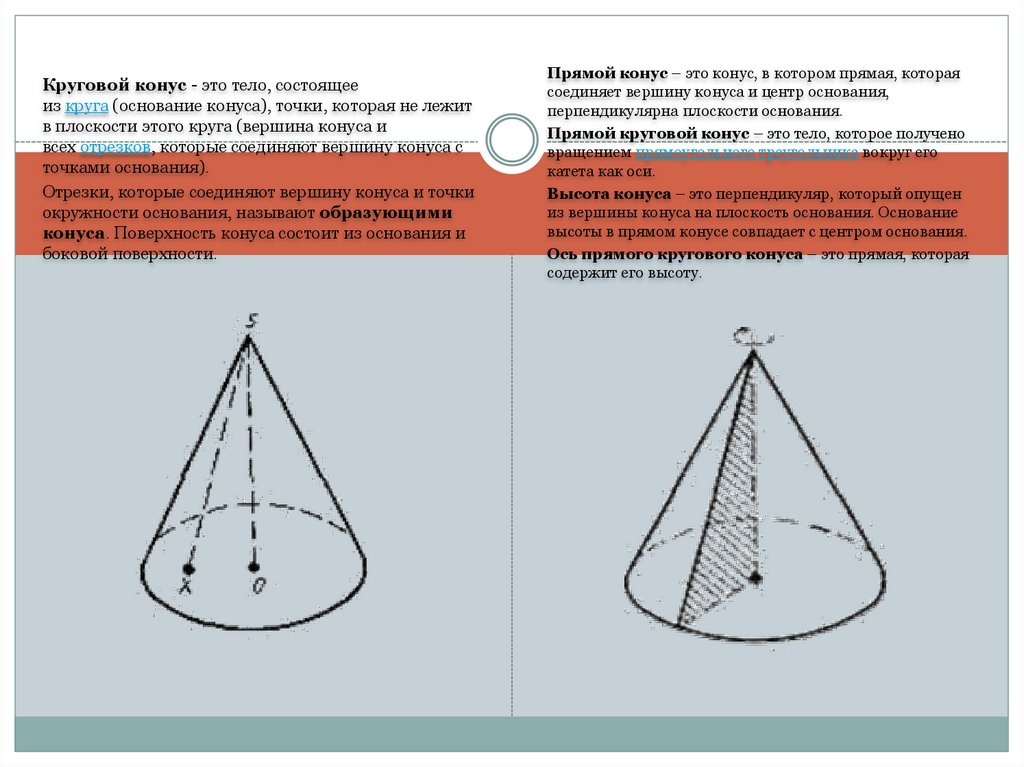
Круговой конус - это тело, состоящееиз круга (основание конуса), точки, которая не лежит
в плоскости этого круга (вершина конуса и
всех отрезков, которые соединяют вершину конуса с
точками основания).
Отрезки, которые соединяют вершину конуса и точки
окружности основания, называют образующими
конуса. Поверхность конуса состоит из основания и
боковой поверхности.
Прямой конус – это конус, в котором прямая, которая
соединяет вершину конуса и центр основания,
перпендикулярна плоскости основания.
Прямой круговой конус – это тело, которое получено
вращением прямоугольного треугольника вокруг его
катета как оси.
Высота конуса – это перпендикуляр, который опущен
из вершины конуса на плоскость основания. Основание
высоты в прямом конусе совпадает с центром основания.
Ось прямого кругового конуса – это прямая, которая
содержит его высоту.
6.
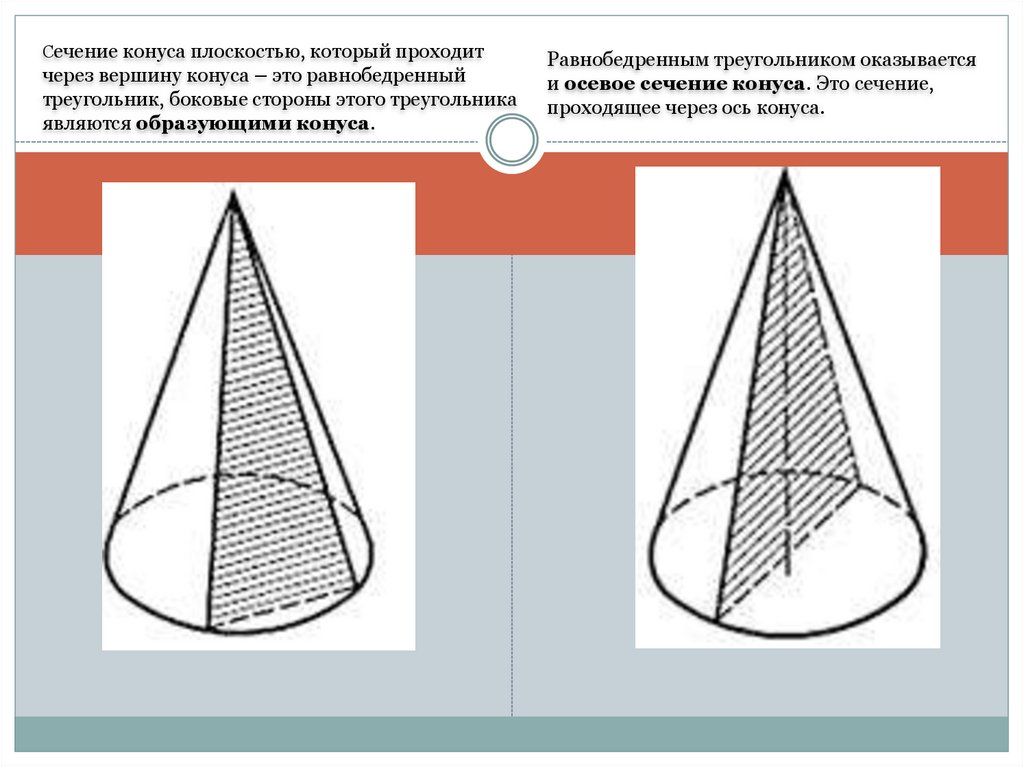
Сечение конуса плоскостью, который проходитчерез вершину конуса – это равнобедренный
треугольник, боковые стороны этого треугольника
являются образующими конуса.
Равнобедренным треугольником оказывается
и осевое сечение конуса. Это сечение,
проходящее через ось конуса.
7.
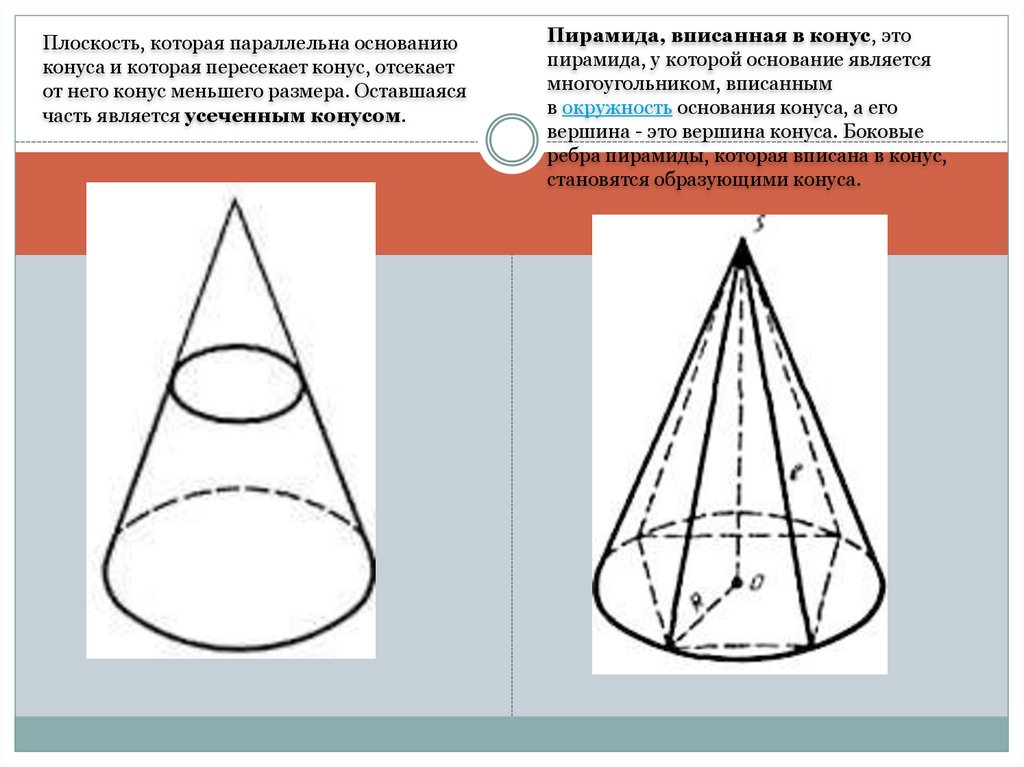
Плоскость, которая параллельна основаниюконуса и которая пересекает конус, отсекает
от него конус меньшего размера. Оставшаяся
часть является усеченным конусом.
Пирамида, вписанная в конус, это
пирамида, у которой основание является
многоугольником, вписанным
в окружность основания конуса, а его
вершина - это вершина конуса. Боковые
ребра пирамиды, которая вписана в конус,
становятся образующими конуса.
8.
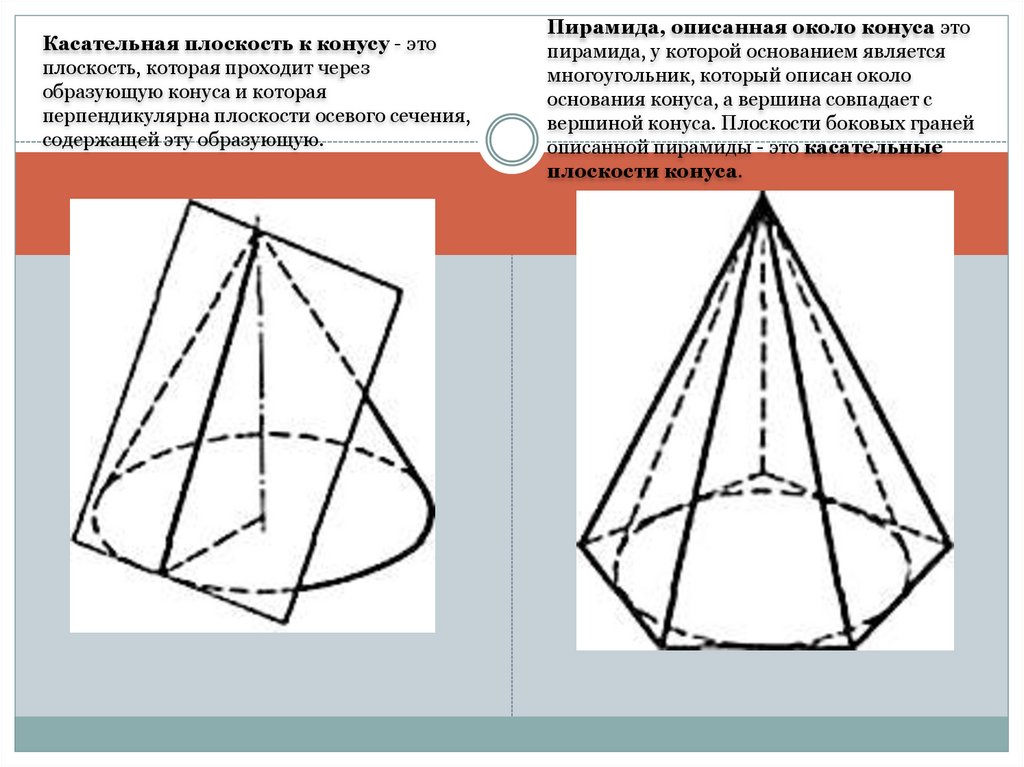
Касательная плоскость к конусу - этоплоскость, которая проходит через
образующую конуса и которая
перпендикулярна плоскости осевого сечения,
содержащей эту образующую.
Пирамида, описанная около конуса это
пирамида, у которой основанием является
многоугольник, который описан около
основания конуса, а вершина совпадает с
вершиной конуса. Плоскости боковых граней
описанной пирамиды - это касательные
плоскости конуса.
9.
Работу выполнила:Исламова Ксения.




 mathematics
mathematics








