Similar presentations:
Конус. Основание конуса
1.
КонусКонусом называется
геометрическое тело, ограниченное конической поверхностью и кругом с
границей.
Конус может быть получен поворотом прямоугольного треугольника вокруг
одного из катетов на 360°.
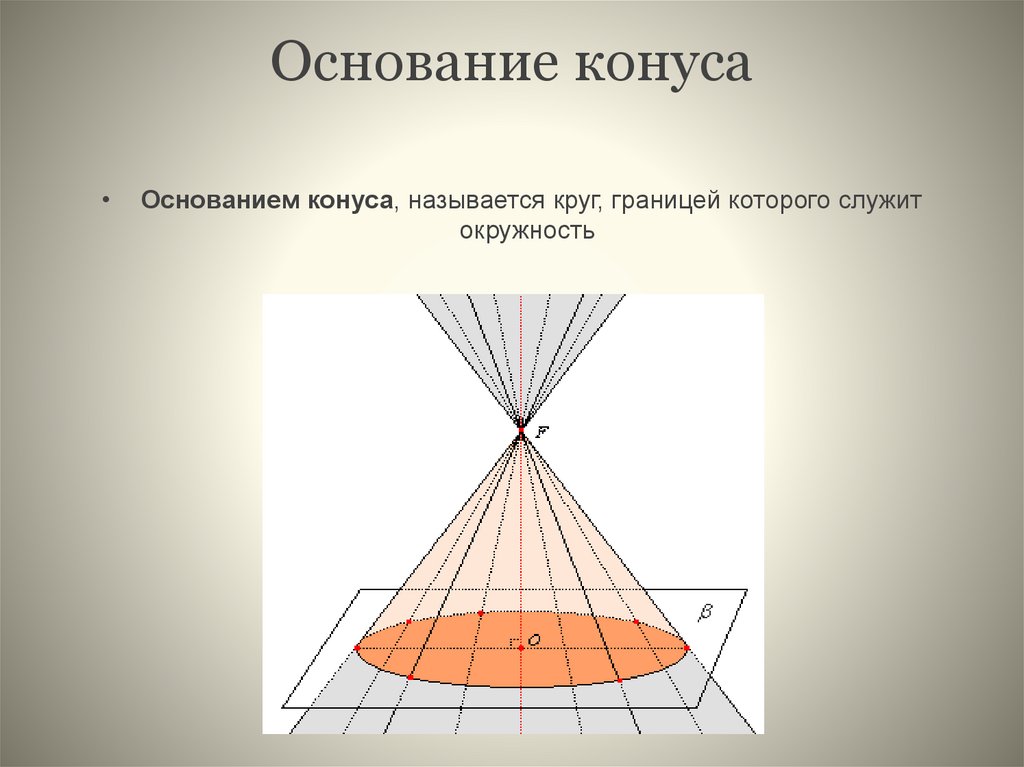
2.
Основание конусаОснованием конуса, называется круг, границей которого служит
окружность
3.
• Образующими конуса называются отрезки коническойповрехности, расположенные между его вершиной и
основанием.
• Вершиной конуса называется вершина F конической
поверхности.
• Высотой конуса называется отрезок FO (или его длина),
где F - вершина конуса, O - центр его основания.
4.
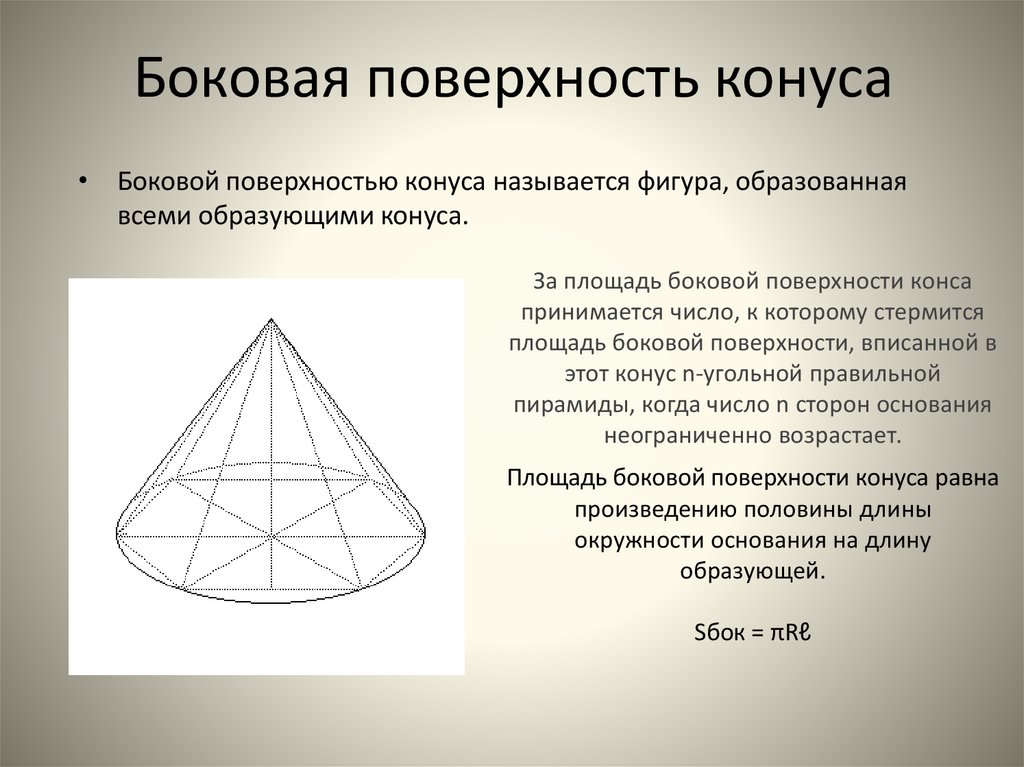
Боковая поверхность конуса• Боковой поверхностью конуса называется фигура, образованная
всеми образующими конуса.
За площадь боковой поверхности конса
принимается число, к которому стермится
площадь боковой поверхности, вписанной в
этот конус n-угольной правильной
пирамиды, когда число n сторон основания
неограниченно возрастает.
Площадь боковой поверхности конуса равна
произведению половины длины
окружности основания на длину
образующей.
Sбок = πRℓ
5.
Сечение конусаЕсли плоскость проходит через высоту
конуса FO, то сечение конуса этой
плоскостью называют осевым и
представляет собой равнобедренный
треугольник, основанием которого является
диаметр основания конуса, а боковыми
сторонами - образующие конуса.
Если плоскость проходит через
внутреннюю точку высоты FO конуса и
перпендикулярна ей, то сечением конуса
является круг, центр которого есть точка
пересечения высоты и этой плоскости.
6.
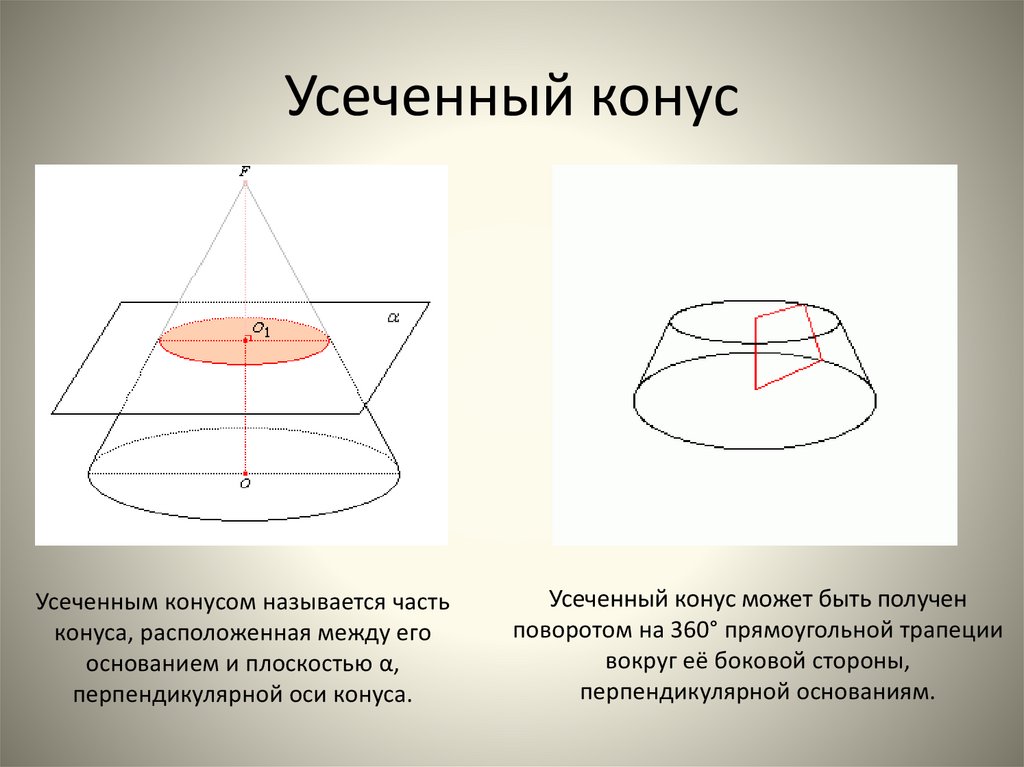
Усеченный конусУсеченным конусом называется часть
конуса, расположенная между его
основанием и плоскостью α,
перпендикулярной оси конуса.
Усеченный конус может быть получен
поворотом на 360° прямоугольной трапеции
вокруг её боковой стороны,
перпендикулярной основаниям.
7.
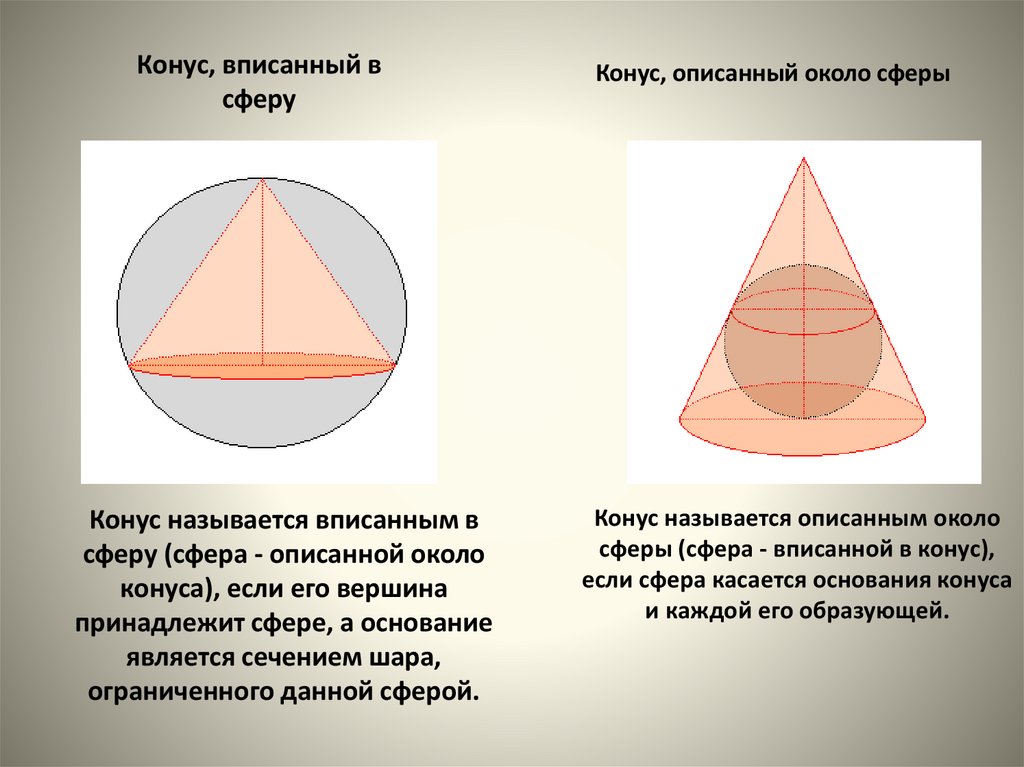
Конус, вписанный всферу
Конус называется вписанным в
сферу (сфера - описанной около
конуса), если его вершина
принадлежит сфере, а основание
является сечением шара,
ограниченного данной сферой.
Конус, описанный около сферы
Конус называется описанным около
сферы (сфера - вписанной в конус),
если сфера касается основания конуса
и каждой его образующей.
8.
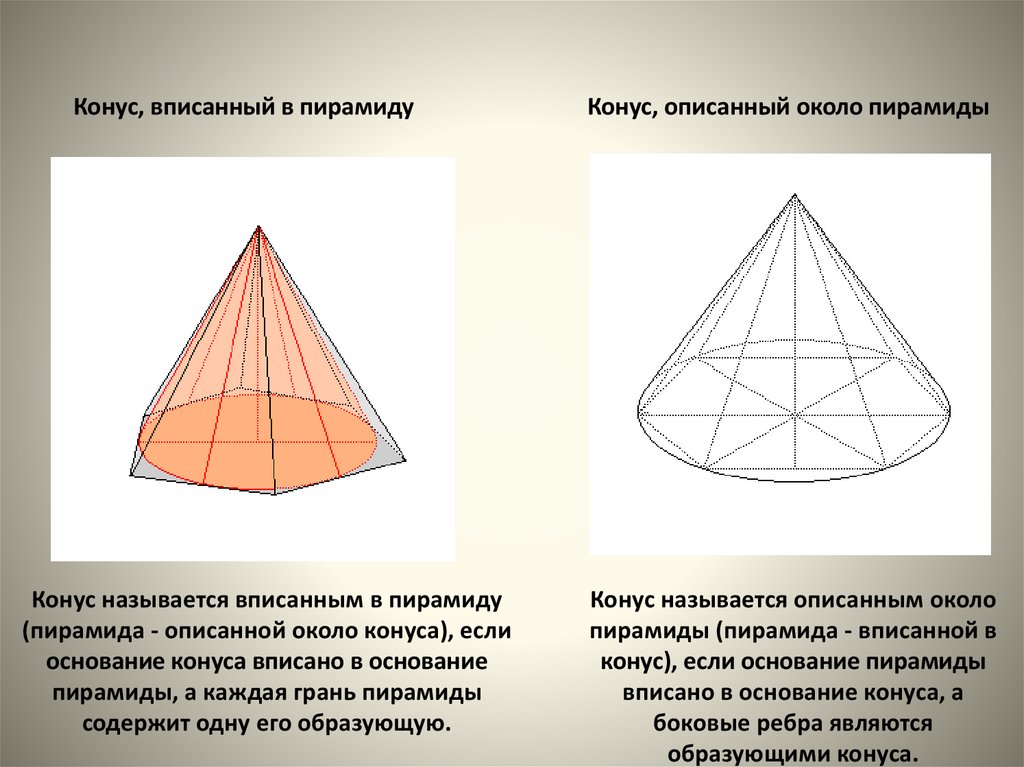
Конус, вписанный в пирамидуКонус называется вписанным в пирамиду
(пирамида - описанной около конуса), если
основание конуса вписано в основание
пирамиды, а каждая грань пирамиды
содержит одну его образующую.
Конус, описанный около пирамиды
Конус называется описанным около
пирамиды (пирамида - вписанной в
конус), если основание пирамиды
вписано в основание конуса, а
боковые ребра являются
образующими конуса.
9.
Объём конусаЗа объём конуса принимается число, к которому стремится
объём правильной пирамиды, вписанной в конус, когда
число сторон основания пирамиды неограниченно
возрастает.
Объём конуса равен одной трети
произведения площади основания на высоту.
V = ⅓ πR2H.




 mathematics
mathematics








