Конус

1. КОНУС

2.

В данной презентации рассмотрены понятия конуса и
его элементов, «поверхность конуса», формула площади
поверхности конуса, сечения конуса плоскостями.
Рассмотрены понятия пирамиды, описанной около
конуса и пирамиды, вписанной в конус (так как данные
комбинации конуса и многогранника часто встречаются в
ЕГЭ).
Задачи взяты из открытого банка заданий для
подготовки к ЕГЭ.
Что должно быть в конспекте по теме «Конус»:
1) определение;
2) чертеж конуса с указанием и обозначением его
элементов;
3) сечения конуса (чертежи);
4) формулы для вычисления площади боковой
поверхности конуса и площади полной поверхности
конуса.

3. Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной отрезками,

соединяющими каждую
точку окружности с вершиной конуса.

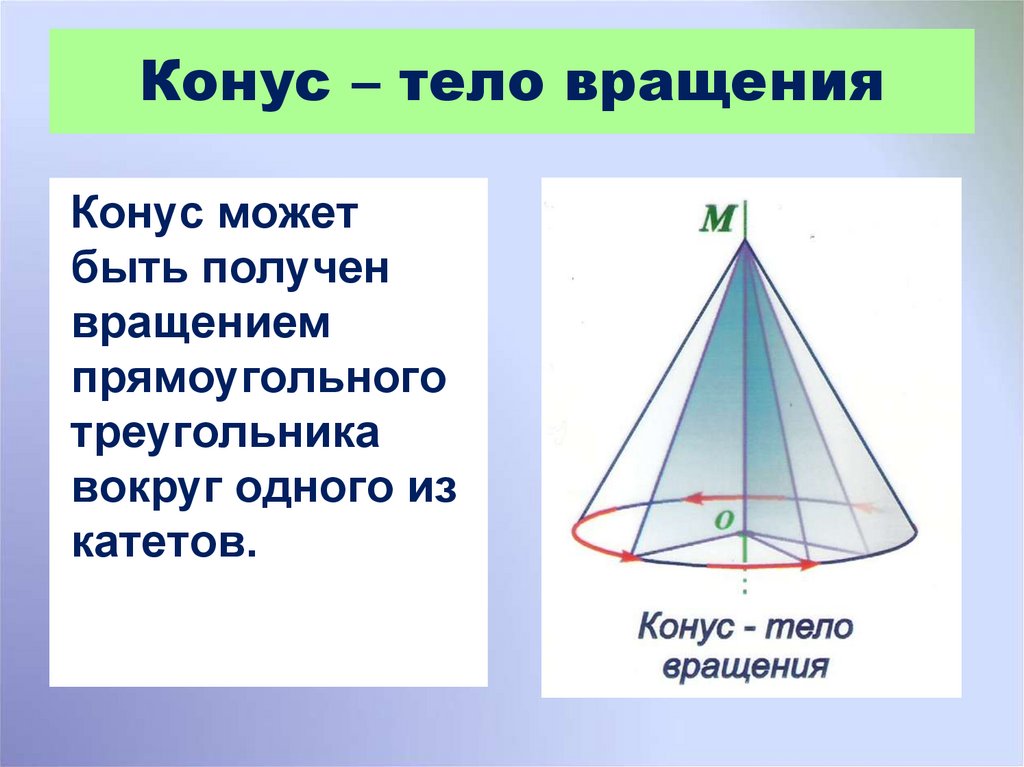
4. Конус – тело вращения

Конус может
быть получен
вращением
прямоугольного
треугольника
вокруг одного из
катетов.

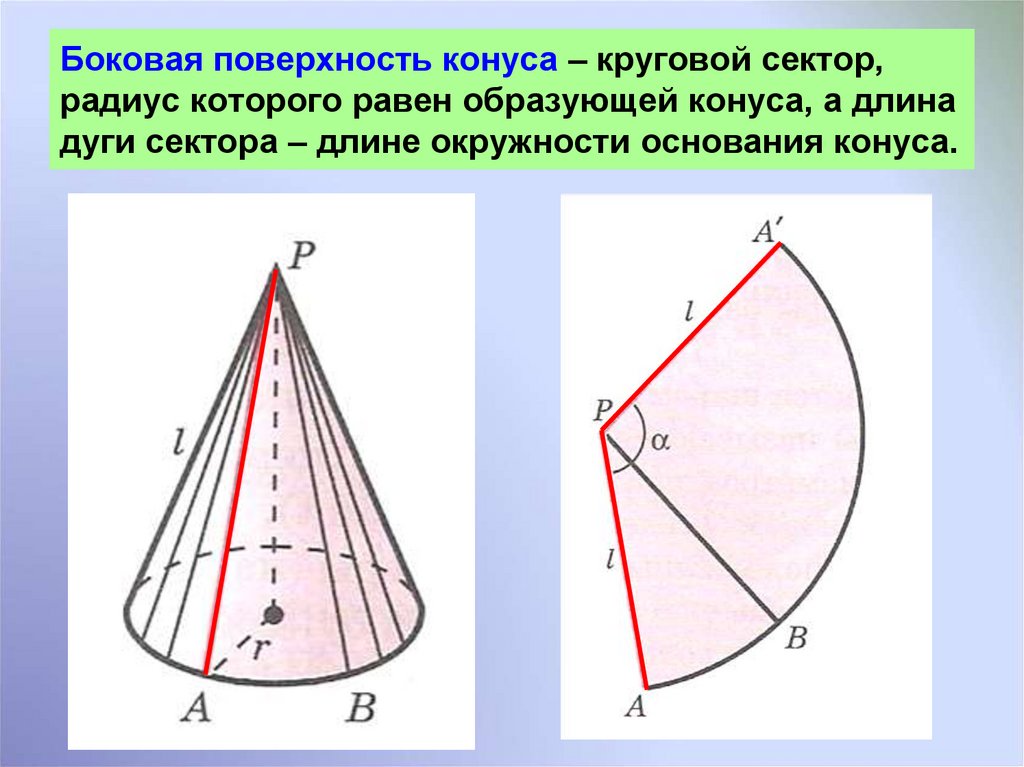
5. Боковая поверхность конуса – круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора – длине окружности

основания конуса.

6.

Боковая поверхность конуса
Площадь боковой
поверхности
конуса равна
произведению
половины длины
окружности
основания на
образующую:
S бок rl

7.

Полная поверхность конуса
Площадь полной
поверхности конуса
равна сумме
площадей боковой
поверхности и
основания:
Sкон. Sосн. Sбок.
Sкон. r rl
2

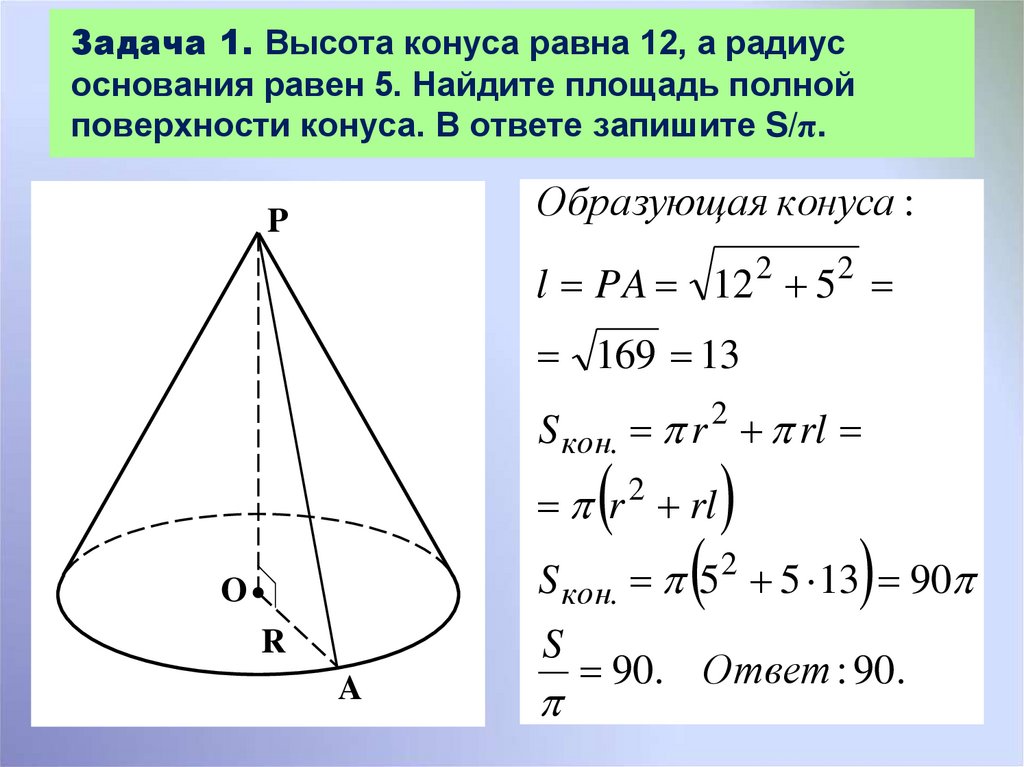
8. Задача 1. Высота конуса равна 12, а радиус основания равен 5. Найдите площадь полной поверхности конуса. В ответе запишите S/π.

Образующая конуса :
P
l PA 12 2 52
169 13
S кон. r 2 rl
r rl
2
S кон. 5 5 13 90
O
S
R
A
2
90. Ответ : 90.

9. Сечения конуса различными плоскостями

Секущая плоскость
проходит через ось
конуса.
Осевое сечение –
равнобедренный
треугольник,
основание которого –
диаметр основания
конуса, а боковые
стороны –
образующие конуса.

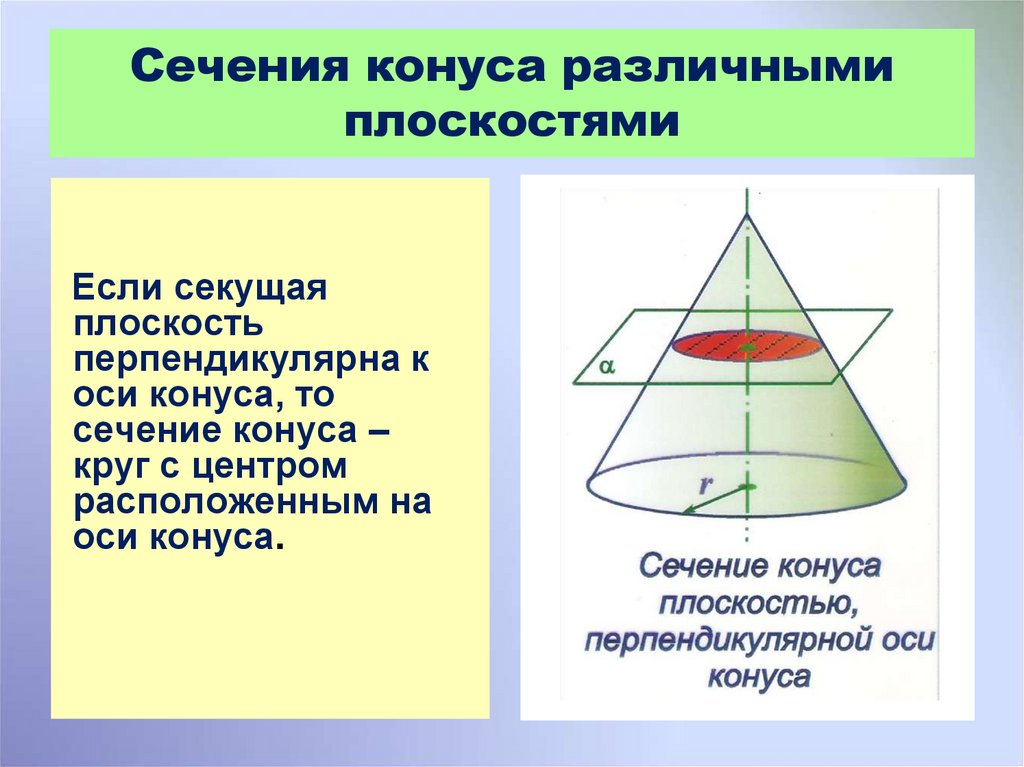
10. Сечения конуса различными плоскостями

Если секущая
плоскость
перпендикулярна к
оси конуса, то
сечение конуса –
круг с центром
расположенным на
оси конуса.

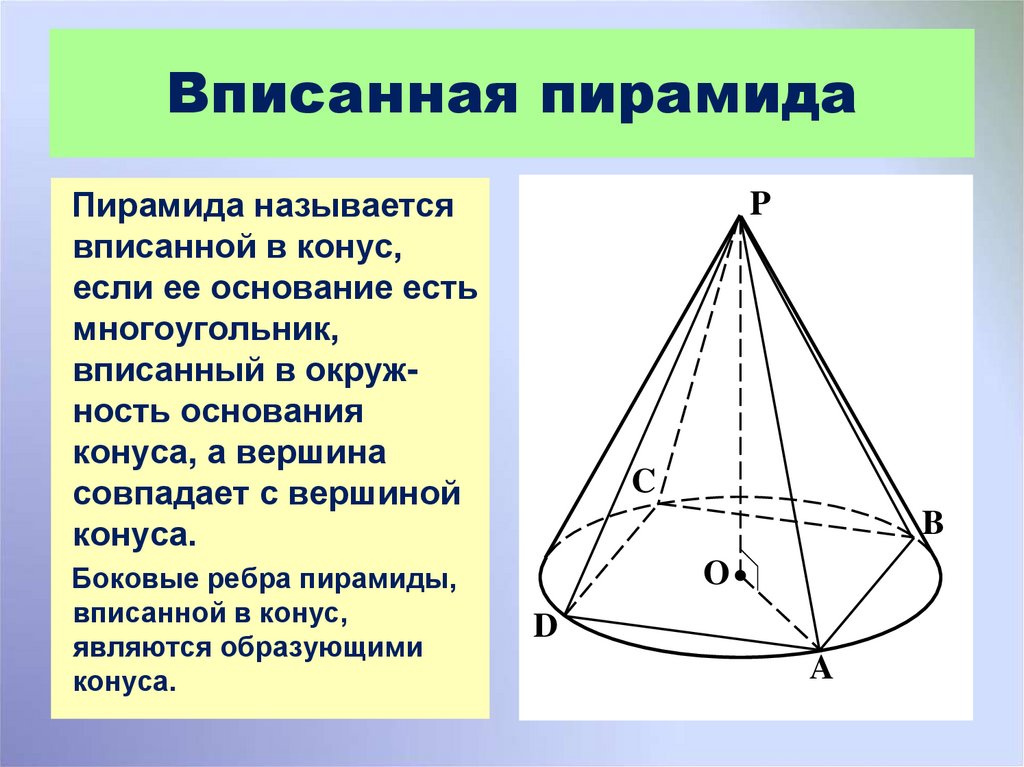
11. Вписанная пирамида

Пирамида называется
вписанной в конус,
если ее основание есть
многоугольник,
вписанный в окружность основания
конуса, а вершина
совпадает с вершиной
конуса.
Боковые ребра пирамиды,
вписанной в конус,
являются образующими
конуса.
P
C
B
O
D
A

12. Описанная пирамида

Пирамида называется
описанной около конуса, если ее основание
есть многоугольник,
описанный около
основания конуса, а
вершина совпадает с
вершиной конуса.
Плоскости боковых граней
описанной пирамиды
являются касательными
плоскостями конуса.
P
C
D
O
B
H
A

13. Задача 2

Вокруг конуса описана правильная
четырехугольная пирамида. Найдите
полную поверхность пирамиды, если
радиус основания конуса равен 6, а
образующая конуса равна 10.

14. Задача 2. Выполняем рисунок

P
C
C
D
B
O
H
O
B
H
A
D
A

15. Задача 2. Решение

Образующая конуса равна
апофеме пирамиды:
P
l PH 10
S пир. S осн. S бок.
a AD 2r 2 6 12
S осн. a 2 12 2 144
C
S бок.
D
O
B
H
A
1
Pосн. l
2
1
4 12 10 240
2
S пир. 144 240 384
Ответ : 384 .

16. Задача 3

В конус вписана правильная
четырехугольная пирамида. Найдите
полную поверхность конуса, если
боковое ребро пирамиды равно 15, а ее
высота равна 9. В ответе запишите S/π.

17.

Задача 3. Выполняем рисунок
P
C
B
O
H
C
B
D
O
D
A
A

18.

Задача 3. Решение
Образующая конуса :
l PA 15
P
Радиус основания
r PA2 OA2 15 2 9 2
144 12
S кон. r 2 rl
C
B
O
r 2 rl
S кон. 12 2 12 15 234
D
A
S
234 . Ответ : 234 .