Конус. Решение задач

1. КОНУС

Решение задач
Автор:
преподаватель математики
Расходова О.Ф.

2.

ТЕОРЕМА ПИФАГОРА: В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов
В прямоугольном треугольнике синус острого угла
равен отношению противолежащего катета к
гипотенузе, косинус угла равен отношению
прилежащего катета к гипотенузе.
В прямоугольном треугольнике катет, лежащий
напротив угла 30° равен половине гипотенузы.
Площадь прямоугольного треугольника равна
половине произведения катетов
Площадь треугольника равна половине произведения
стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения
сторон на синус угла между ними

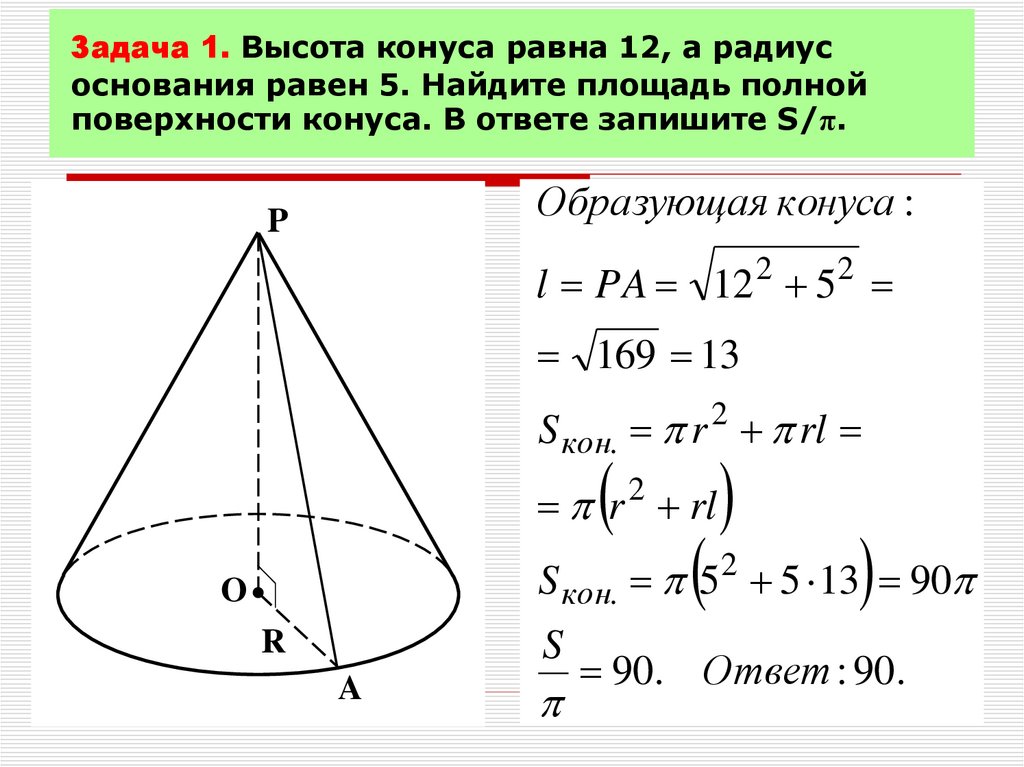
3. Задача 1. Высота конуса равна 12, а радиус основания равен 5. Найдите площадь полной поверхности конуса. В ответе запишите S/π.

Образующая конуса :
P
l PA 12 2 52
169 13
S кон. r 2 rl
r rl
2
S кон. 5 5 13 90
O
S
R
A
2
90. Ответ : 90.

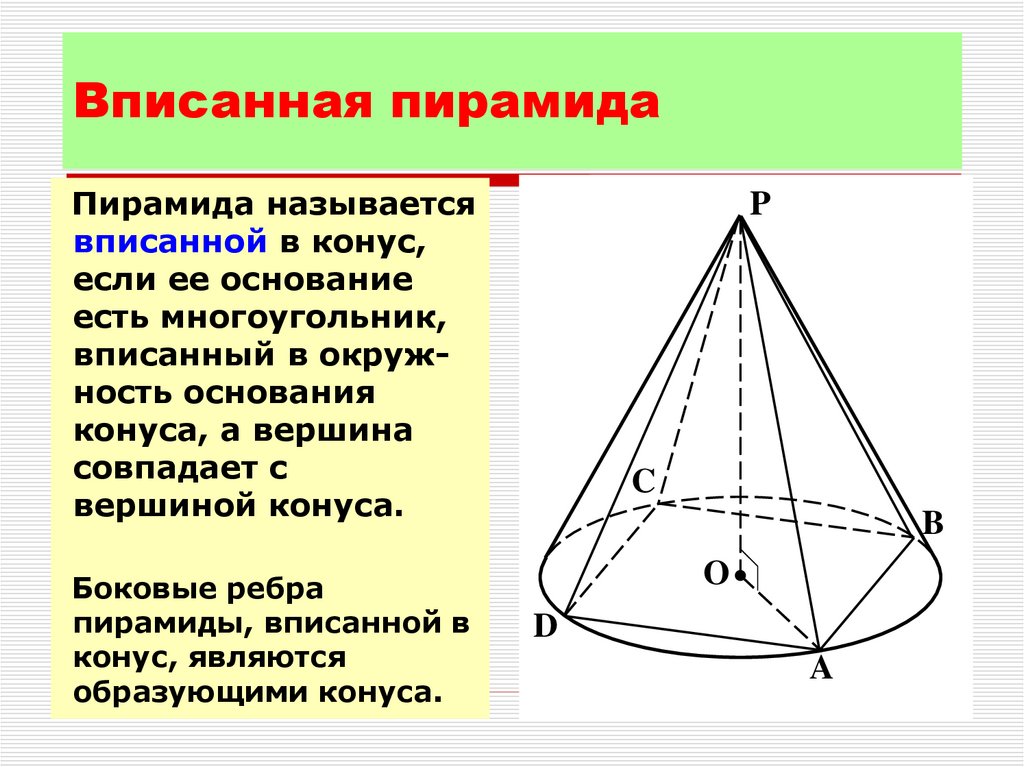
4. Вписанная пирамида

Пирамида называется
вписанной в конус,
если ее основание
есть многоугольник,
вписанный в окружность основания
конуса, а вершина
совпадает с
вершиной конуса.
Боковые ребра
пирамиды, вписанной в
конус, являются
образующими конуса.
P
C
B
O
D
A

5. Описанная пирамида

Пирамида называется
описанной около
конуса, если ее
основание есть
многоугольник,
описанный около
основания конуса, а
вершина совпадает с
вершиной конуса.
Плоскости боковых
граней описанной
пирамиды являются
касательными
плоскостями конуса.
P
C
D
O
B
H
A

6. Задача 2

Вокруг конуса описана правильная
четырехугольная пирамида.
Найдите полную поверхность
пирамиды, если радиус основания
конуса равен 6, а образующая
конуса равна 10.

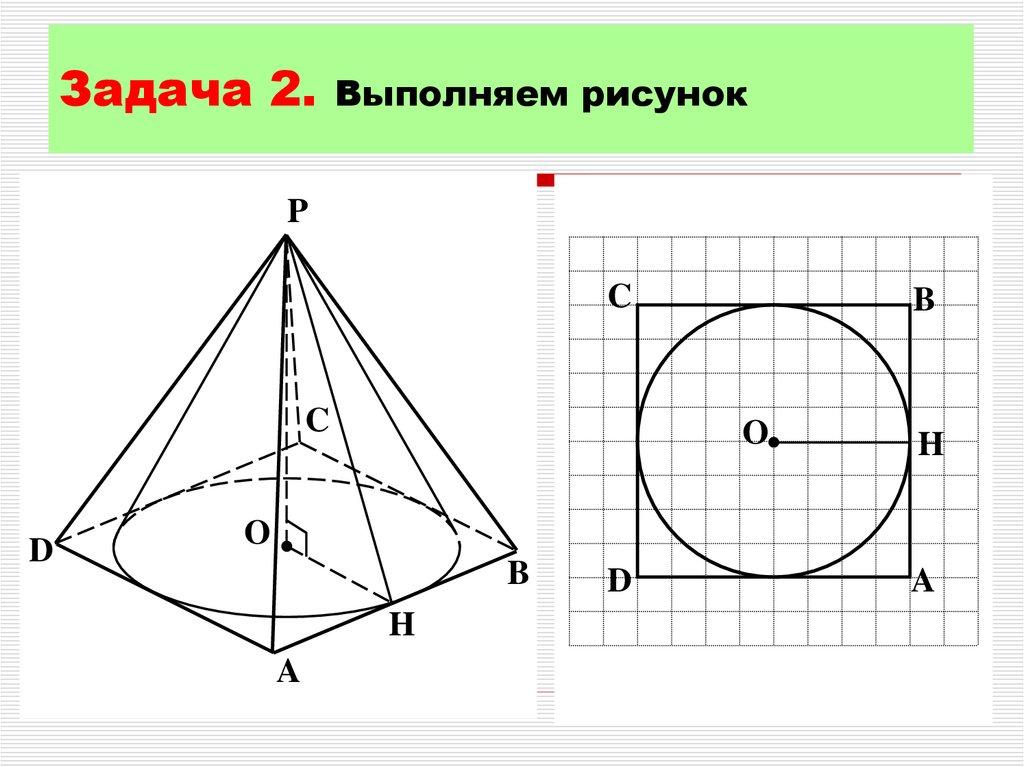
7. Задача 2. Выполняем рисунок

P
C
C
D
B
O
H
O
B
H
A
D
A

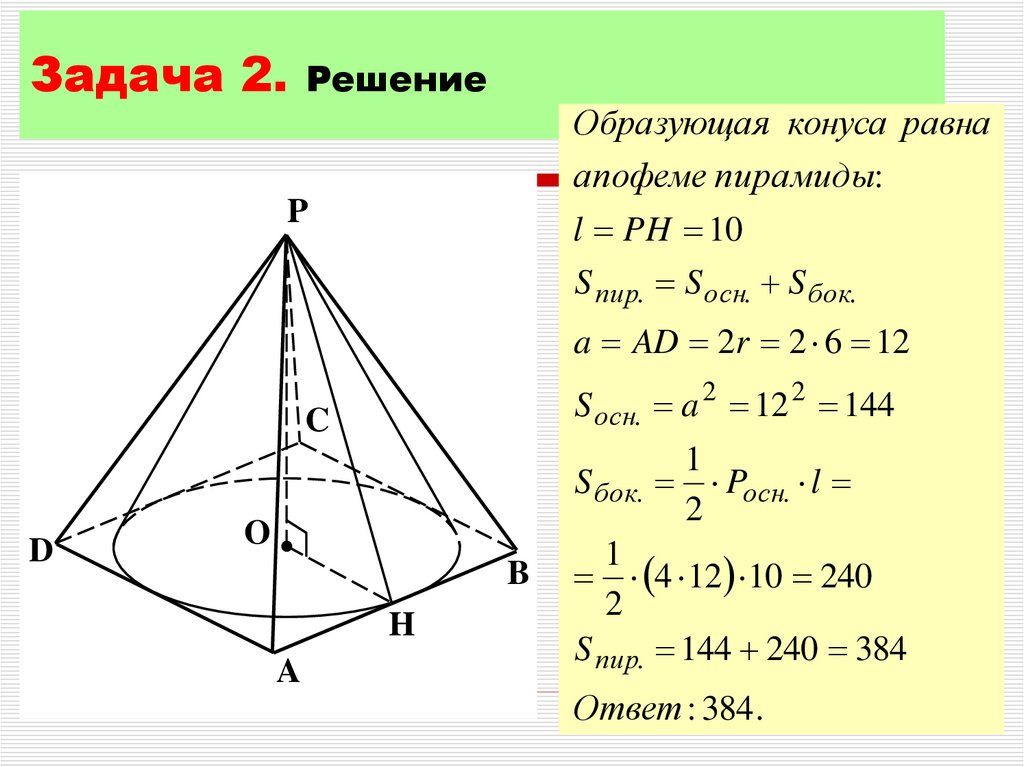
8. Задача 2. Решение

Образующая конуса равна
апофеме пирамиды:
l PH 10
S пир. S осн. S бок.
P
a AD 2r 2 6 12
S осн. a 2 12 2 144
C
D
O
B
H
A
1
S бок. Pосн. l
2
1
4 12 10 240
2
S пир. 144 240 384
Ответ : 384 .

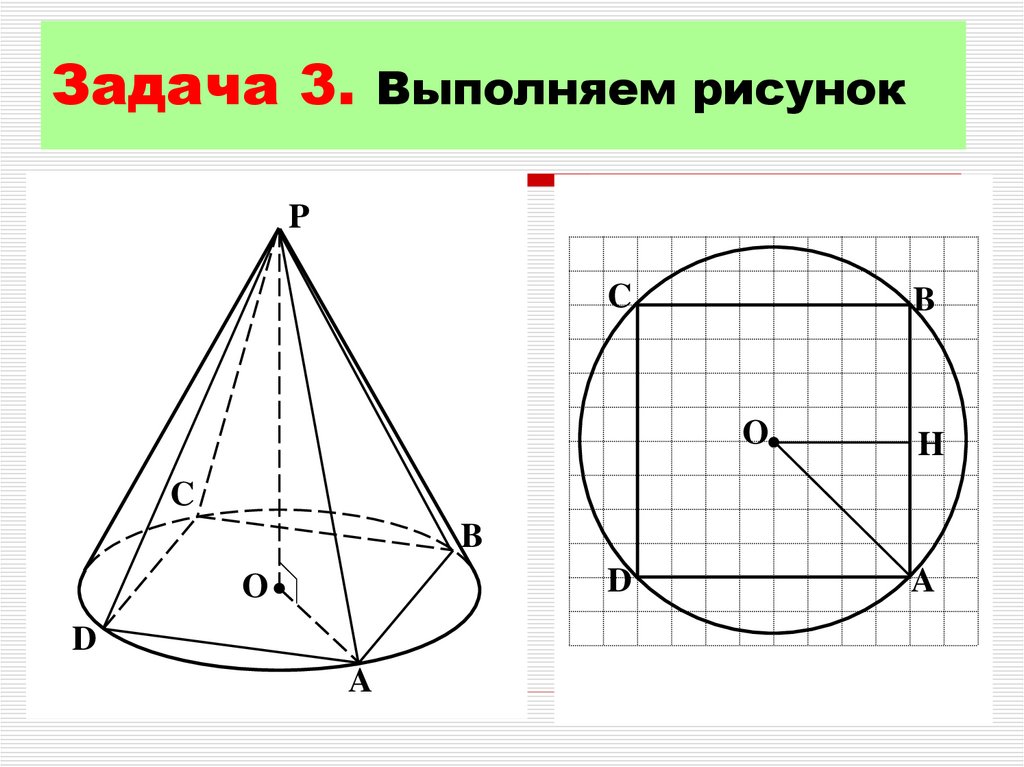
9. Задача 3

В конус вписана правильная
четырехугольная пирамида.
Найдите полную поверхность
конуса, если боковое ребро
пирамиды равно 15, а ее высота
равна 9. В ответе запишите S/π.

10.

Задача 3. Выполняем рисунок
P
C
B
O
H
C
B
D
O
D
A
A

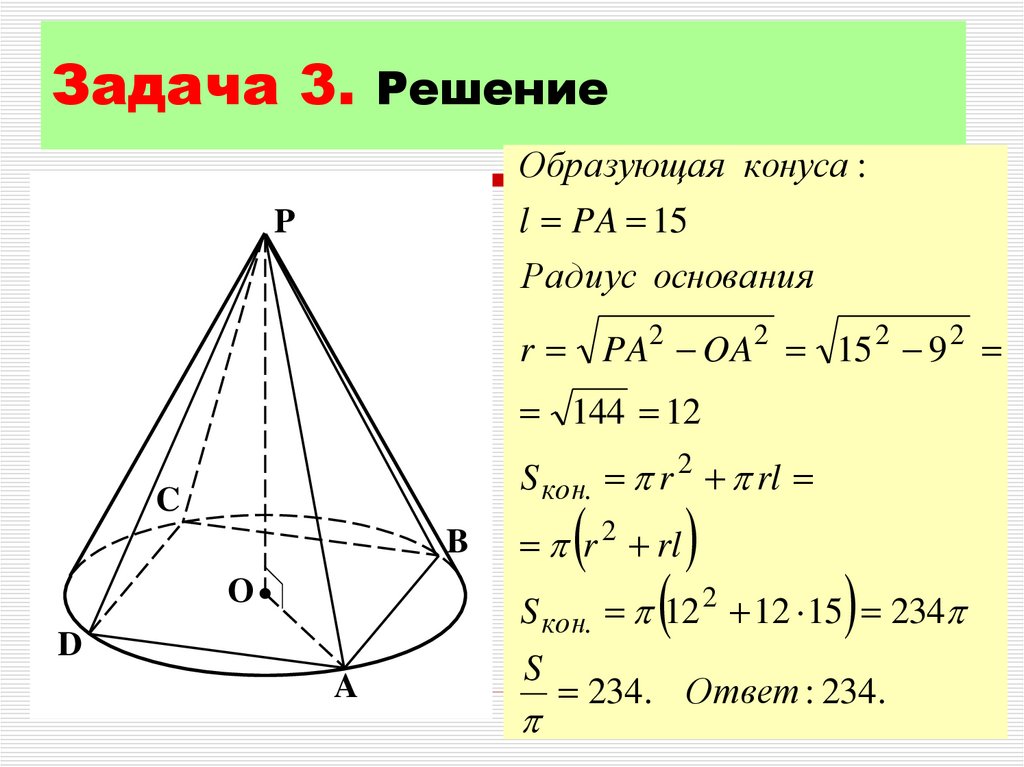
11.

Задача 3. Решение
Образующая конуса :
l PA 15
Радиус основания
P
r PA2 OA2 15 2 9 2
144 12
S кон. r 2 rl
C
B
O
r 2 rl
S кон. 12 2 12 15 234
D
A
S
234 . Ответ : 234 .

12.

Задача 4.
Образующая конуса равна 13 см, а радиус основания – 5 см.
Найдите площадь полной поверхности и объем конуса.
ΔАОВ – прямоугольный, найдем ВО по теореме Пифагора.
BО 2 АВ 2 АO 2
1
V R2 H
3
В
BО 2 132 52
H 12
R 5
Sбок Rl Sбок 5 13
S полн Rl R
Sполн 65 25
13
А
BО 12
l 13
2
5
О
С
1
V 52 12
3

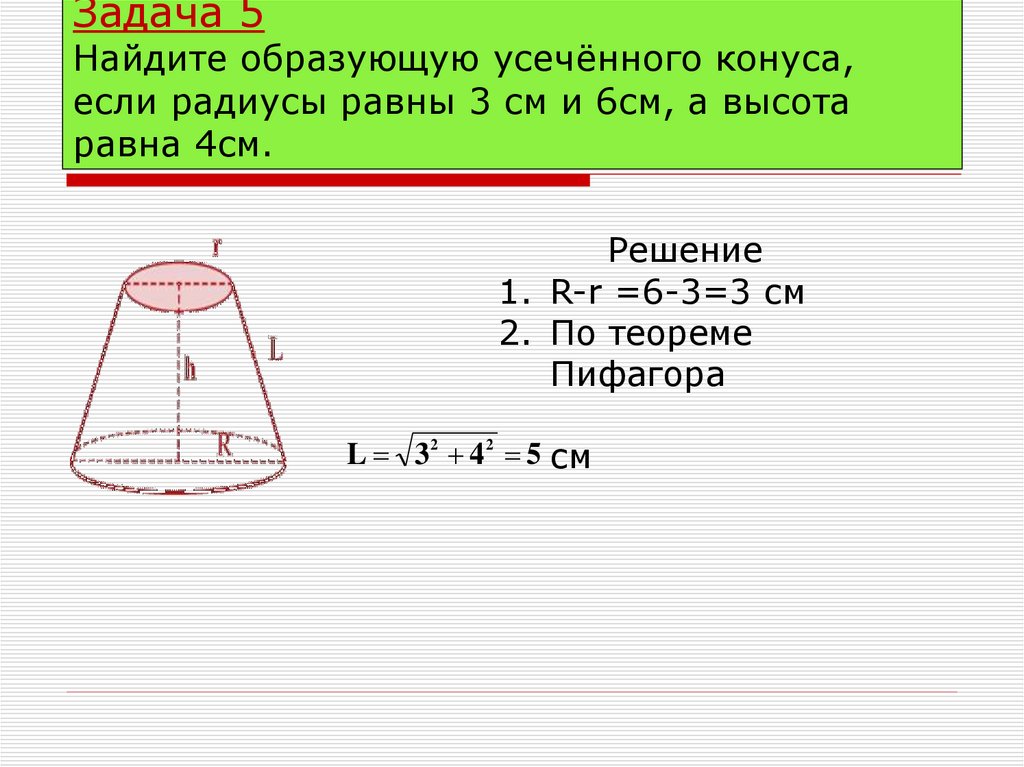
13. Задача 5 Найдите образующую усечённого конуса, если радиусы равны 3 см и 6см, а высота равна 4см.

Решение
1. R-r =6-3=3 см
2. По теореме
Пифагора
L 3 2 4 2 5 см

14. Задача 6. Высота конуса равна 8, а диаметр основания – 30. Найдите образующую конуса.

15. Задача 7. Образующая конуса равна 10, а диаметр основания – 12. Найдите высоту конуса.