Similar presentations:
Прямоугольник, ромб, квадрат
1.
2.
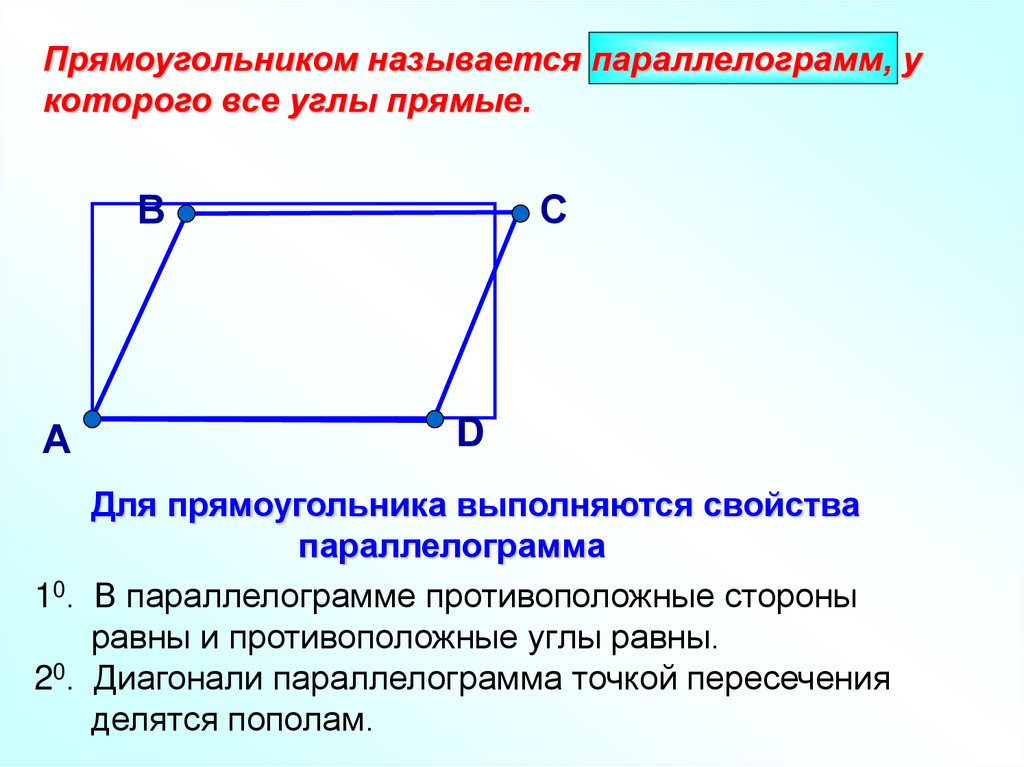
Прямоугольником называется параллелограмм, укоторого все углы прямые.
В
А
С
D
Для прямоугольника выполняются свойства
параллелограмма
10. В параллелограмме противоположные стороны
равны и противоположные углы равны.
20. Диагонали параллелограмма точкой пересечения
делятся пополам.
3.
Особое свойство прямоугольника.Диагонали прямоугольника равны.
С
В
Дано: ABCD
прямоугольник
Доказать: АС = ВD
Доказательство:
D
А
АD – общая сторона
АВ=СD, как противолежащие стороны
АСD = DBA по катетам
Значит, АС = ВD.
4.
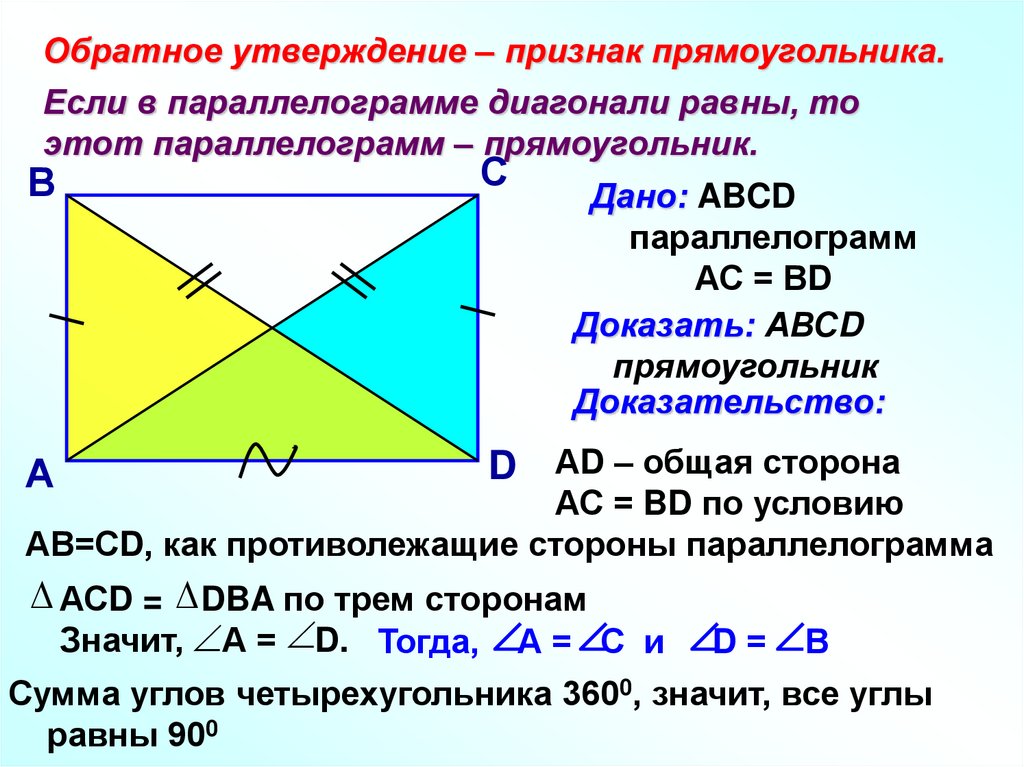
Обратное утверждение – признак прямоугольника.Если в параллелограмме диагонали равны, то
этот параллелограмм – прямоугольник.
В
С
А
D АD – общая сторона
Дано: ABCD
параллелограмм
АС = ВD
Доказать: АВСD
прямоугольник
Доказательство:
АС = BD по условию
АВ=СD, как противолежащие стороны параллелограмма
АСD = DBA по трем сторонам
Значит, А = D. Тогда, А = С и
D= В
Сумма углов четырехугольника 3600, значит, все углы
равны 900
5.
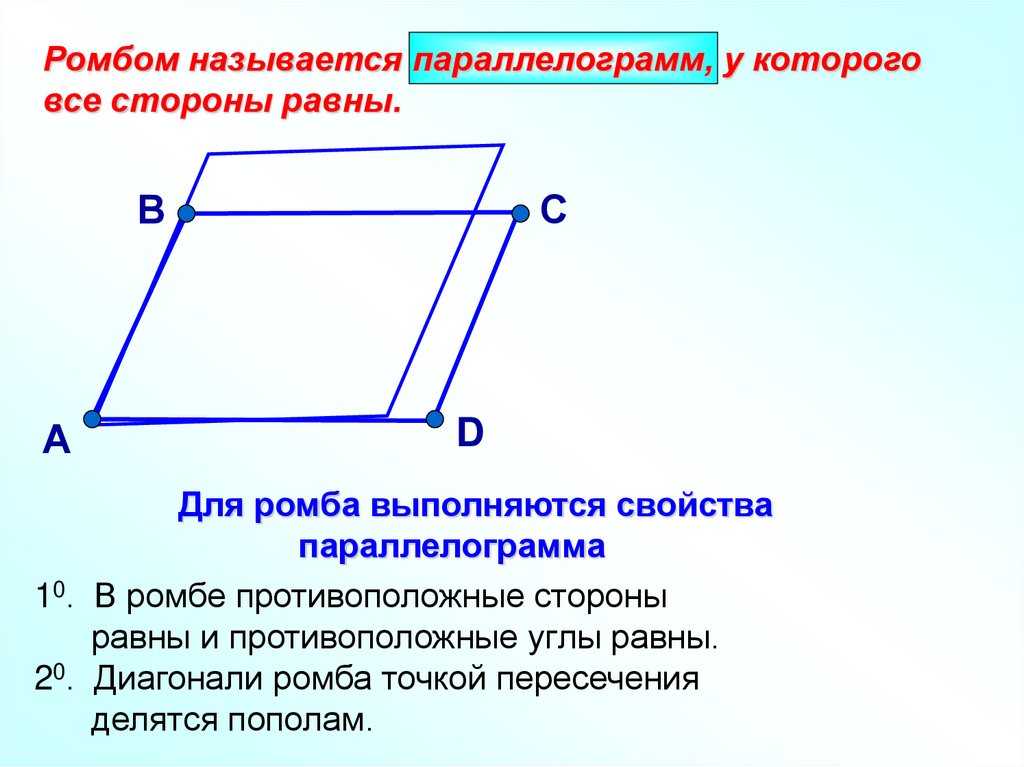
Ромбом называется параллелограмм, у котороговсе стороны равны.
В
А
С
D
Для ромба выполняются свойства
параллелограмма
10. В ромбе противоположные стороны
равны и противоположные углы равны.
20. Диагонали ромба точкой пересечения
делятся пополам.
6.
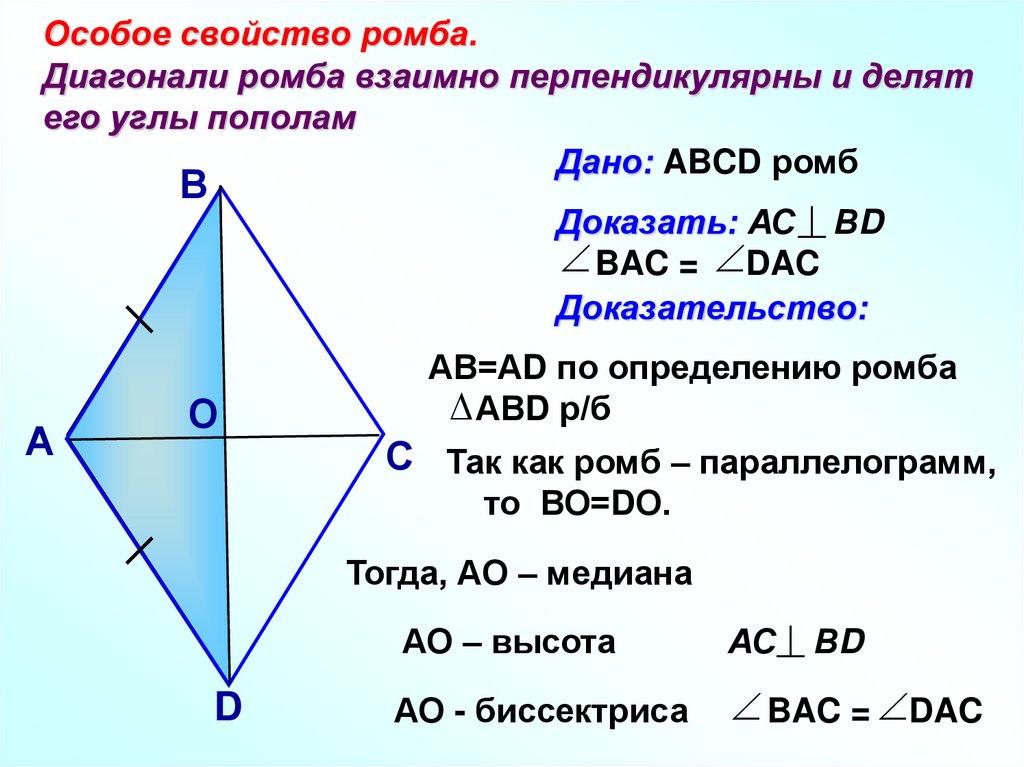
Особое свойство ромба.Диагонали ромба взаимно перпендикулярны и делят
его углы пополам
Дано: ABCD ромб
В
А
Доказать: АС ВD
BAC = DAC
Доказательство:
О
АВ=АD по определению ромба
АВD р/б
С Так как ромб – параллелограмм,
то ВО=DО.
Тогда, АО – медиана
D
АО – высота
АС ВD
АО - биссектриса
BAC = DAC
7.
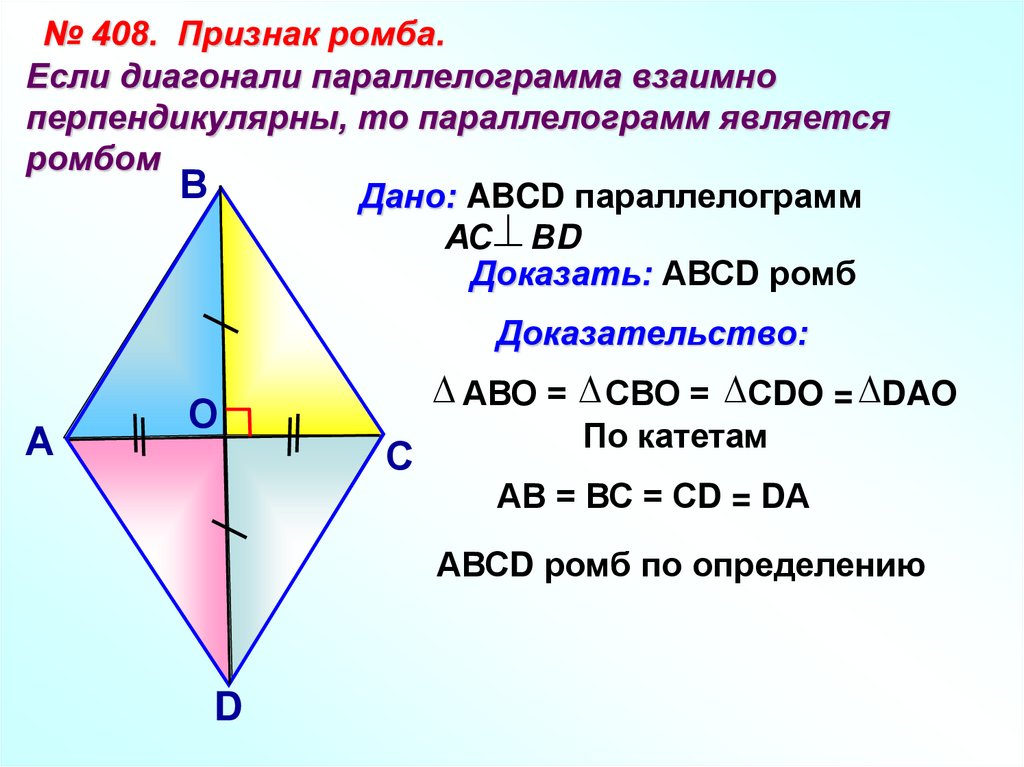
№ 408. Признак ромба.Если диагонали параллелограмма взаимно
перпендикулярны, то параллелограмм является
ромбом
В
Дано: ABCD параллелограмм
АС ВD
Доказать: АВСD ромб
Доказательство:
А
О
АВО = СВО = СDO = DAO
С
По катетам
АВ = ВС = СD = DА
АВСD ромб по определению
D
8.
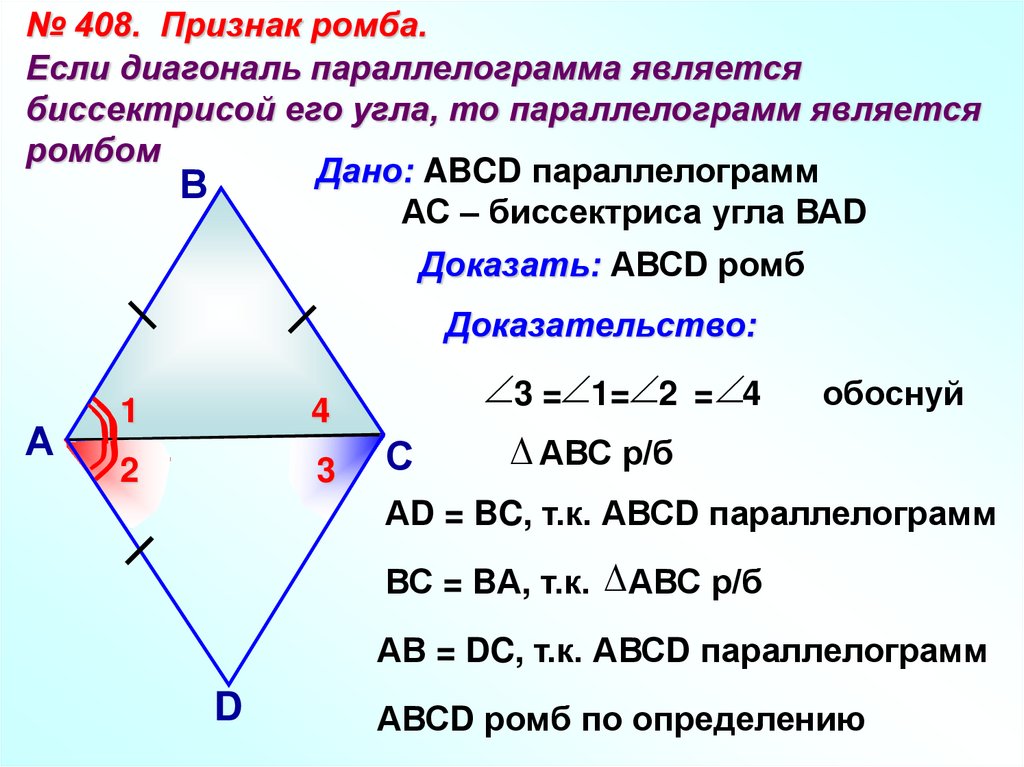
№ 408. Признак ромба.Если диагональ параллелограмма является
биссектрисой его угла, то параллелограмм является
ромбом
Дано: ABCD параллелограмм
В
АС – биссектриса угла ВАD
Доказать: АВСD ромб
Доказательство:
А
1
4
2
3
3 = 1= 2 = 4
С
обоснуй
АВС р/б
АD = BC, т.к. АВСD параллелограмм
ВС = BА, т.к. АВС р/б
АВ = DC, т.к. АВСD параллелограмм
D
АВСD ромб по определению
9.
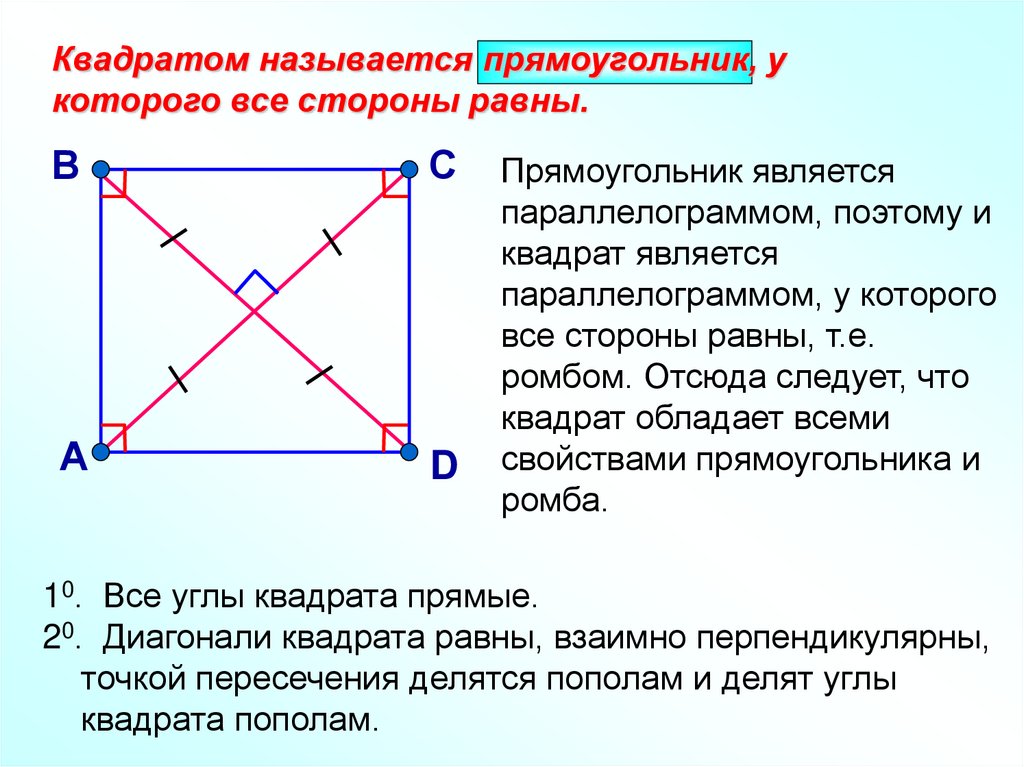
Квадратом называется прямоугольник, укоторого все стороны равны.
В
С
А
D
Прямоугольник является
параллелограммом, поэтому и
квадрат является
параллелограммом, у которого
все стороны равны, т.е.
ромбом. Отсюда следует, что
квадрат обладает всеми
свойствами прямоугольника и
ромба.
10. Все углы квадрата прямые.
20. Диагонали квадрата равны, взаимно перпендикулярны,
точкой пересечения делятся пополам и делят углы
квадрата пополам.
10. Признаки квадрата
• Если в прямоугольнике диагоналиперпендикулярны – это квадрат
• Если в ромбе диагонали равны – это
квадрат
• Если в параллелограмме диагонали
перпендикулярны и равны – это квадрат



 mathematics
mathematics








