Решение уравнения теплопроводности

1.

Решение уравнения
теплопроводности
Чистяков Артём
Фт - 210005

2.

Применение уравнения теплопроводности
Уравнение теплопроводности имеет широкое применение, особенно
в области физики. Вот несколько ключевых применений:
1)Физика материалов: Используется для изучения тепловых
свойств различных материалов и влияния теплопроводности на них.
2)Астрофизика: Применяется для моделирования тепловых
процессов в звездах и межзвездном пространстве.
3)Термодинамика и статистическая физика: Используется для
анализа процессов переноса тепла и для расчетов в рамках
термодинамики и статистической физики.
4)Использование в численных моделях: Уравнение
теплопроводности является основой многих численных методов,
которые применяются для моделирования физических систем, где
происходит перенос тепла.

3.

Уравнение теплопроводности
Уравнение диффузии
Двумерное уравнение
теплопроводности

4.

Краевые условия

5.

Методы решения уравнения теплопроводности
Метод Эйлера:
Первая производная:
Конечная формула:
Вторые производные:

6.

Стабильность
Для того, чтобы решение было устойчивым, нужно соблюдать осторожность при выборе шагов по
времени и пространству, так как слишком длинные временные шаги могут привести к
нестабильности системы
Условие стабильности системы

7.

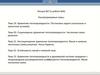
Ошибка по времени в методе Эйлера
dt = 0.1
dt = 0.01

8.

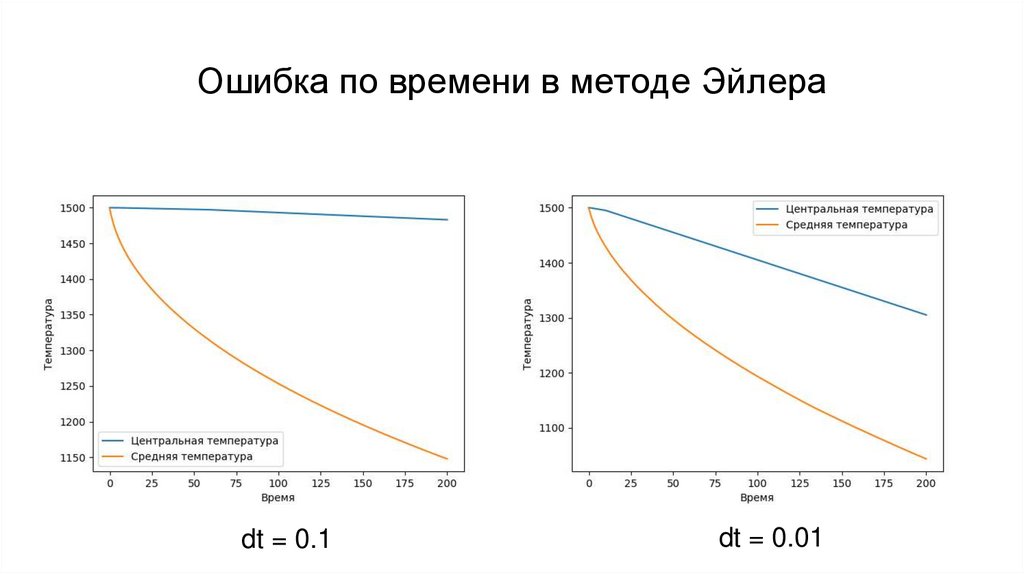
Практическая часть
Распределение температуры по стержню

9.

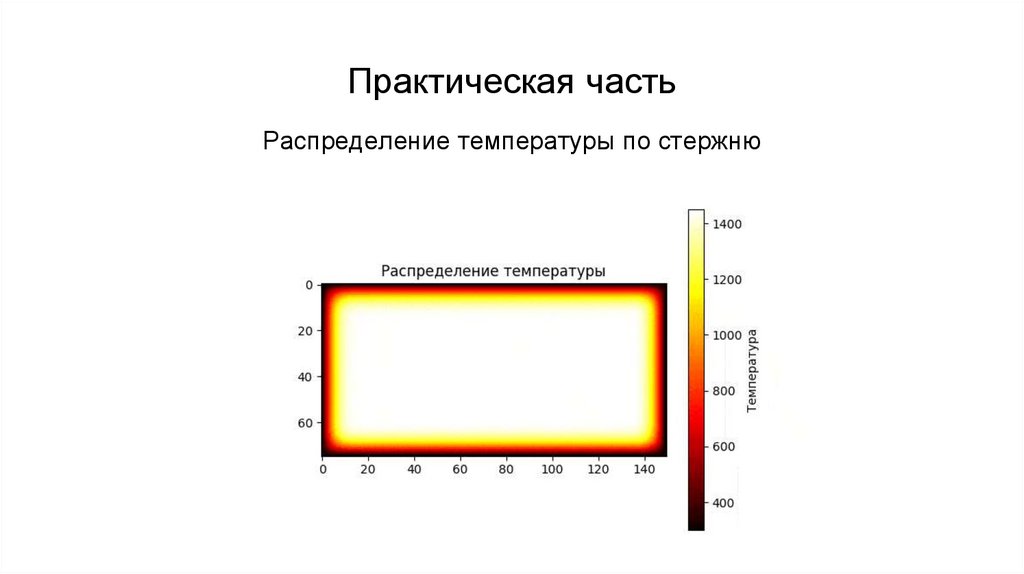
Зависимость температуры от времени

10.

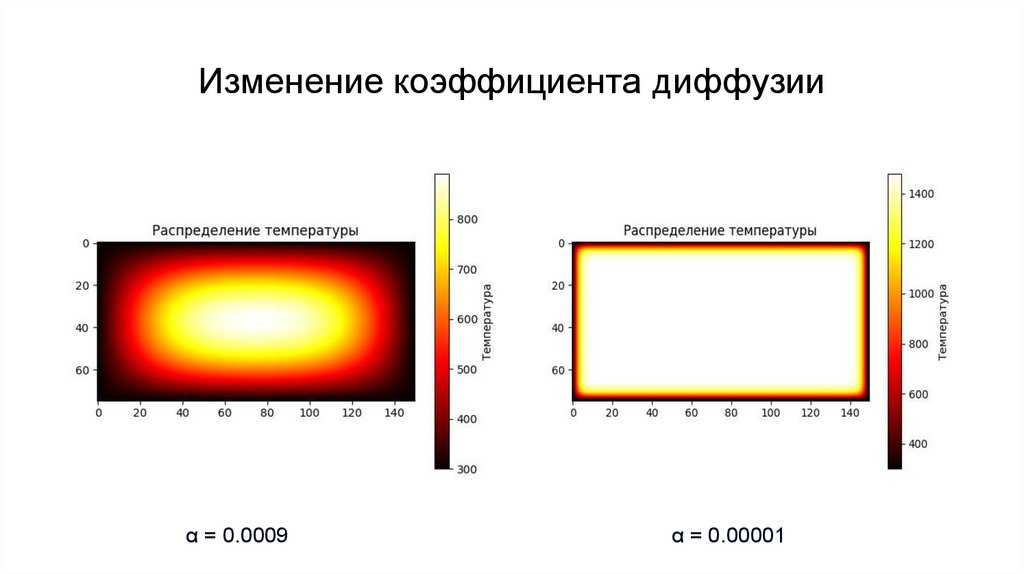
Изменение коэффициента диффузии
α = 0.0009
α = 0.00001

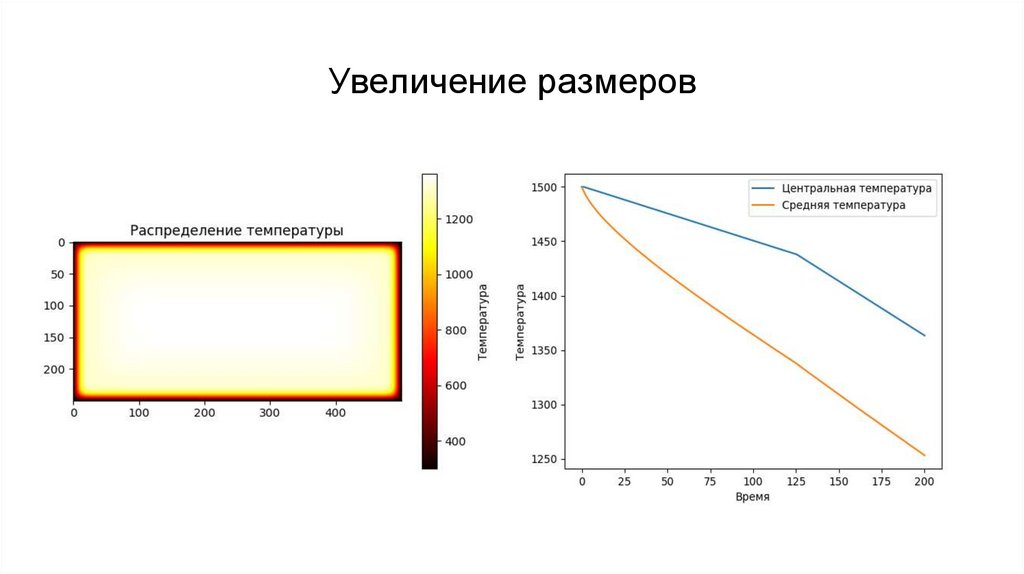
11.

Увеличение размеров

12.

Выводы
1)Решение уравнения теплопроводности с использованием численных
методов, в частности метода Эйлера, позволяет эффективно моделировать
процесс охлаждения стержня. Это подчеркивает важность численных
методов в физическом моделировании.
2)Свойства стержня, такие как коэффициент температуропроводности и
размеры, оказывают значительное влияние на скорость охлаждения и
распределение температуры.