Процессы переноса: диффузия, теплопроводность и вязкость

1. Термодинамика и статистическая физика

2. Лекция № 7

Процессы переноса: диффузия,
теплопроводность и вязкость.
1. Диффузия. Закон Фика. Коэффициент
диффузии. Броуновское движение.
2. Теплопроводность. Закон Фурье.
Коэффициент теплопроводности для газов.
3. Вязкость. Коэффициент вязкости
(внутреннего трения).

3. В процессе диффузии происходит перенос вещества, а при тепло- проводности и при внутреннем трении – перенос энергии. В основе

В процессе диффузии происходит
перенос вещества, а при теплопроводности и при внутреннем
трении – перенос энергии.
В основе этих явлений лежит один
и тот же механизм – хаотическое
движение молекул. Общность
механизма, обуславливающего все эти
явления переноса, приводит к тому,
что их закономерности должны быть
похожи друг на друга.

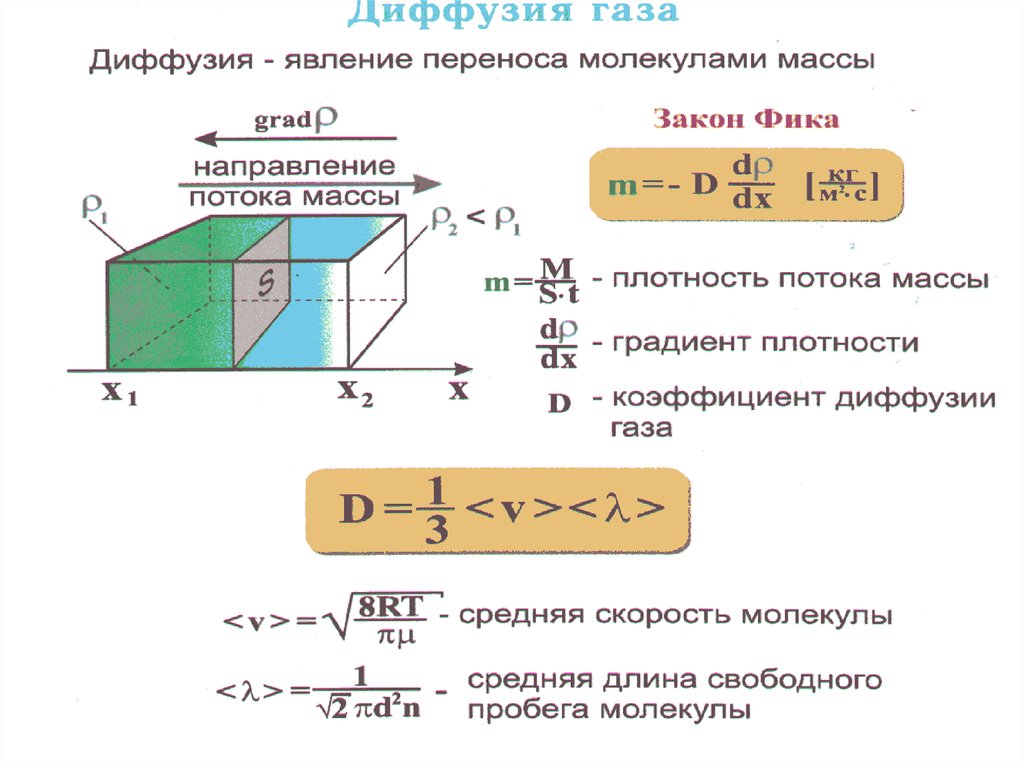
4. Диффузия газов

Диффузия от латинского diffusio –
распространение, растекание взаимное
проникновение соприкасающихся веществ
друг в друга, вследствие теплового
движения частиц вещества.
Диффузия происходит в направлении
уменьшения концентрации вещества и
ведет к его равномерному распределению
по занимаемому объему.

5. Диффузия имеет место в газах, жидкостях и твердых телах. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях,

еще медленнее в твердых
телах, что обусловлено характером
движения частиц в этих средах.
Для газа диффузия
– это
распределение молекул
примеси
от
источника
(или взаимная
диффузия
газа).

6.

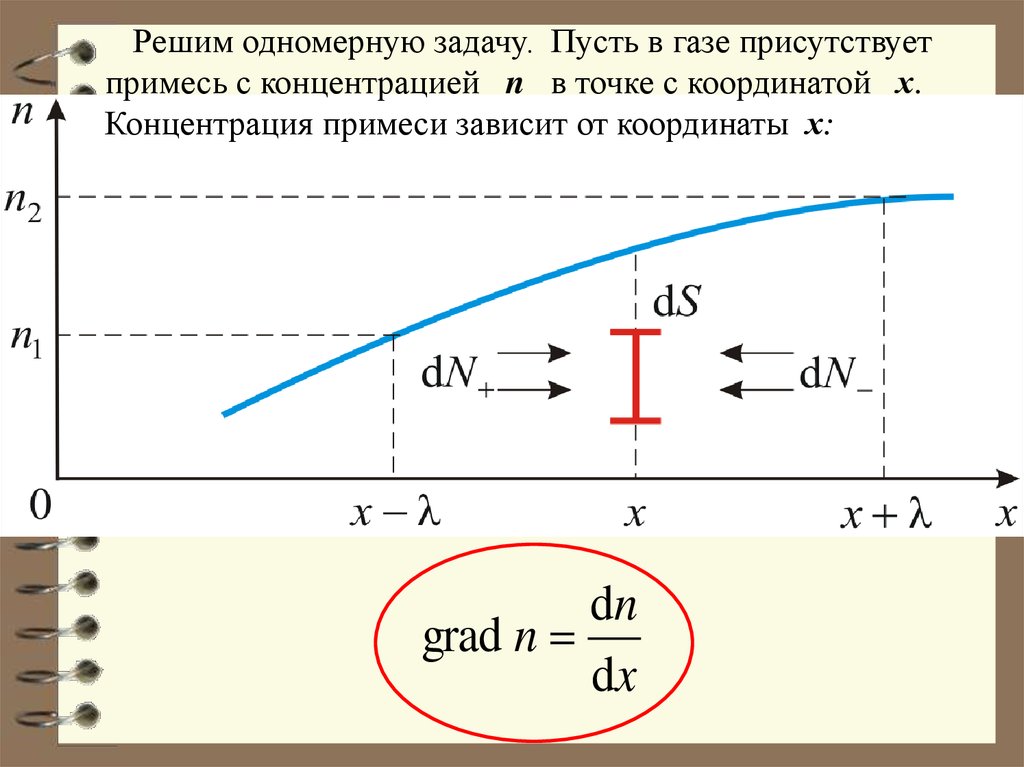
Решим одномерную задачу. Пусть в газе присутствует
примесь с концентрацией n в точке с координатой х.
Концентрация примеси зависит от координаты х:
dn
grad n
dx

7. Градиент концентрации, в общем случае равен: Так как у нас одномер- ная задача, то (модуль): При наличии grad n, хаотическое

Градиент концентрации, в общем случае
равен:
dn dn dn
grad n
i
j k
dx
dy
dz
dn
Так как у нас одномерgrad n
ная задача, то (модуль):
dx
При наличии grad n, хаотическое движение
будет более направленным и возникнет
поток молекул примеси, направленный от
мест с большей концентрацией к местам с
меньшей концентрацией. Найдём этот поток.

8.

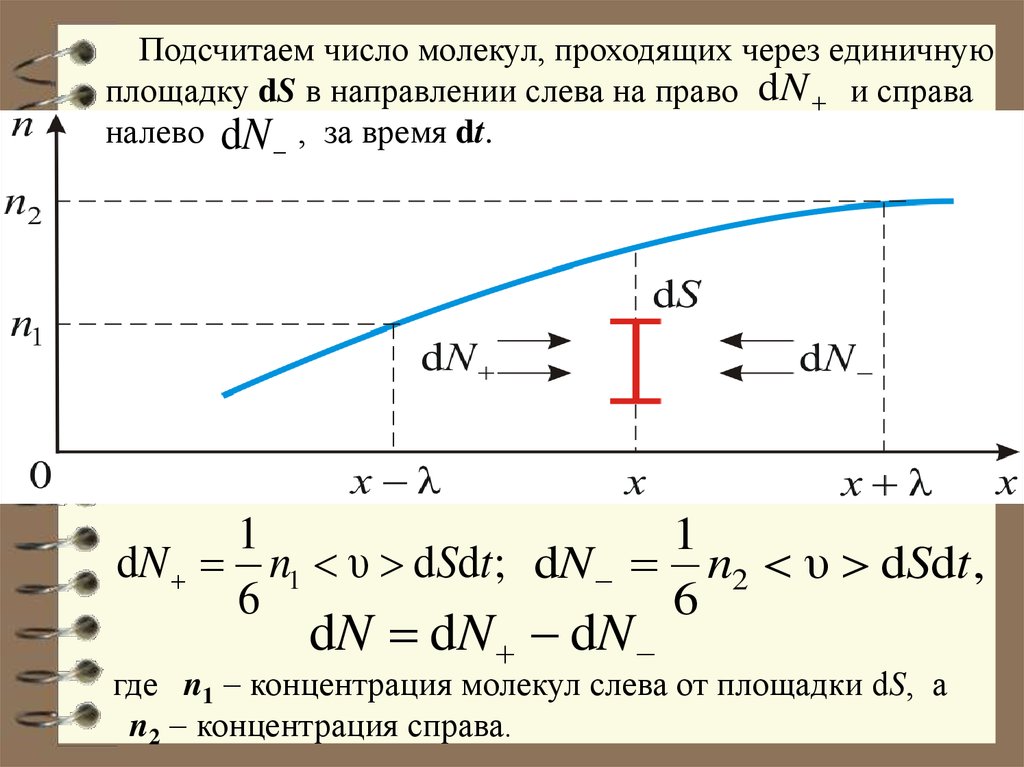
Подсчитаем число молекул, проходящих через единичную
площадку dS в направлении слева на право dN и справа
налево dN , за время dt.
1
1
dN n1 υ dSdt ; dN n2 υ dSdt ,
6
6
dN dN dN
где n1 концентрация молекул слева от площадки dS, а
n2 концентрация справа.

9. Результирующий диффузионный поток через единицу площади в единицу времени: но тогда

dN dN dN
Результирующий диффузионный
поток через единицу площади в единицу
времени:
dN
1
J
dSdt
6
n1 n2 υ
1
n2 n1
J υ
,
3
2
но n2 n 1 dn; 2λ dx, тогда
n2 n1 dn
1
dn
, J υ
3
dx
2
dx

10. Обозначим: – коэффици- ент диффузии. Тогда диффузионный поток будет равен: - закон Фика (одномерный вид) или в общем случае (в

1
Обозначим: D λ υ – коэффици3
ент диффузии.
Тогда диффузионный поток будет
равен:
dn
- закон Фика
J D
dx (одномерный вид)
или в общем случае (в трёхмерный
случай):
J D grad n
- закон Фика
(в общем виде)

11.

Адольф Фик –немецкий учёный XIX
века (1829-1901), приобрел известность в 26 лет (1855 г.) благодаря своей
первой работе в области физики, в которой выдвинул гипотезу о том, что
скорость диффузии газов пропорциональна градиенту их концентрации.
Спустя год он опубликовал монографию
«Die Medizinische Physik», которая на
десятилетия стала энциклопедией по
медицинской физике.
31 год Фик проработал в Вюрцбурге, где создал институт
физиологии, ставший известным во всем мире в качестве
передового центра медицинской науки. Здесь же он
предложил свой метод измерения сердечного выброса,
обессмертивший его имя.

12. Из закона Фика видно, что диффузионный поток, направлен в сторону уменьшения концентрации. При этом коэффициент диффузии D

J D grad n
Из закона Фика видно, что
диффузионный поток, направлен в
сторону уменьшения концентрации.
При этом коэффициент диффузии
D численно равен диффузионному
потоку через единицу площади в
единицу
времени
при
grad n 1
Измеряется
коэффициент
диффузии D в м2/с.

13.

14.

15.

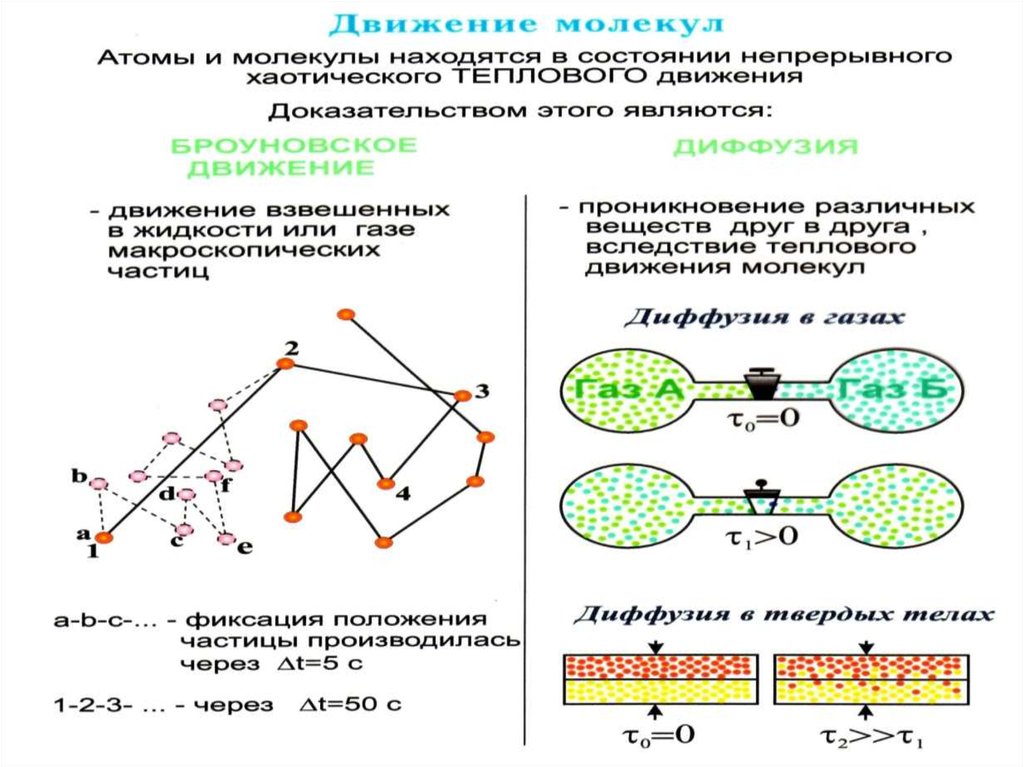
16. Броуновское движение

Броуновское движение в жидкости тем
оживлённее, чем меньше вязкость жидкости. Его едва удаётся подметить в глицерине, а в газах, оно чрезвычайно интенсивно.
Броуновское движение вызывается толчками, испытываемыми взвешенными частицами со стороны окружающих молекул,
совершающих тепловое движение. Под влиянием ударов молекул окружающей среды
скорость броуновской частицы меняется.

17.

Пусть броуновская частица имеет форму
шарика радиуса r . Если небольшой шарик
равномерно движется в жидкости со скоростью υ , то, как показывает опыт и теория,
на него действует сила сопротивления F,
пропорциональная скорости υ. Коэффициент пропорциональности в формуле
В F называется подвижностью
частицы – В.
Подвижность частицы B связана с коэффициентом диффузии соотношеним Эйнштейна:
D kT В

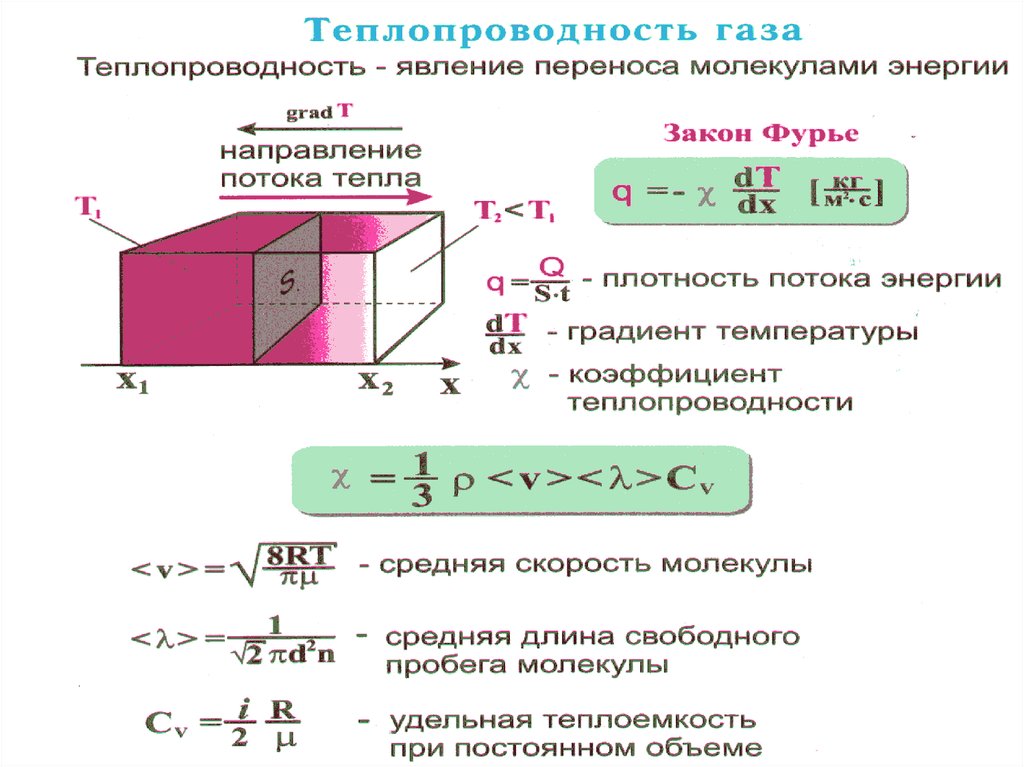
18. Теплопроводность газов

Учение о теплопроводности
начало развиваться в XVIII в. и
получило свое завершение в работах
французского ученого Ж. Фурье
(1768 – 1830), опубликовавшего в
1822 г. книгу «Аналитическая теория
теплоты».

19.

Жан Батист Жозеф Фурье
(1768-1830) — французский
математик и физик,
иностранный почетный член
Петербургской АН (1829).
Труды по алгебре, дифференциальным уравнениям и
математической физике.
В 1807 и 1811 годах он представил Парижской АН свои первые открытия по
теории распространения тепла в твёрдом теле, а в
1822 году опубликовал работу "Аналитическая
теория тепла", сыгравшую большую роль в
последующей истории математики.

20. Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря

хаотическому движению, молекулы в
соседних слоях будут перемешиваться
и, их средние энергии будут
выравниваться. Происходит перенос
энергии от более нагретых слоев к
более холодным.

21. называется теплопроводностью. Поток тепла пропорционален градиенту температуры:

Перенос энергии от более
нагретых слоев к более холодным
называется теплопроводностью.
Поток тепла пропорционален
градиенту температуры:
dT
Q~
dx

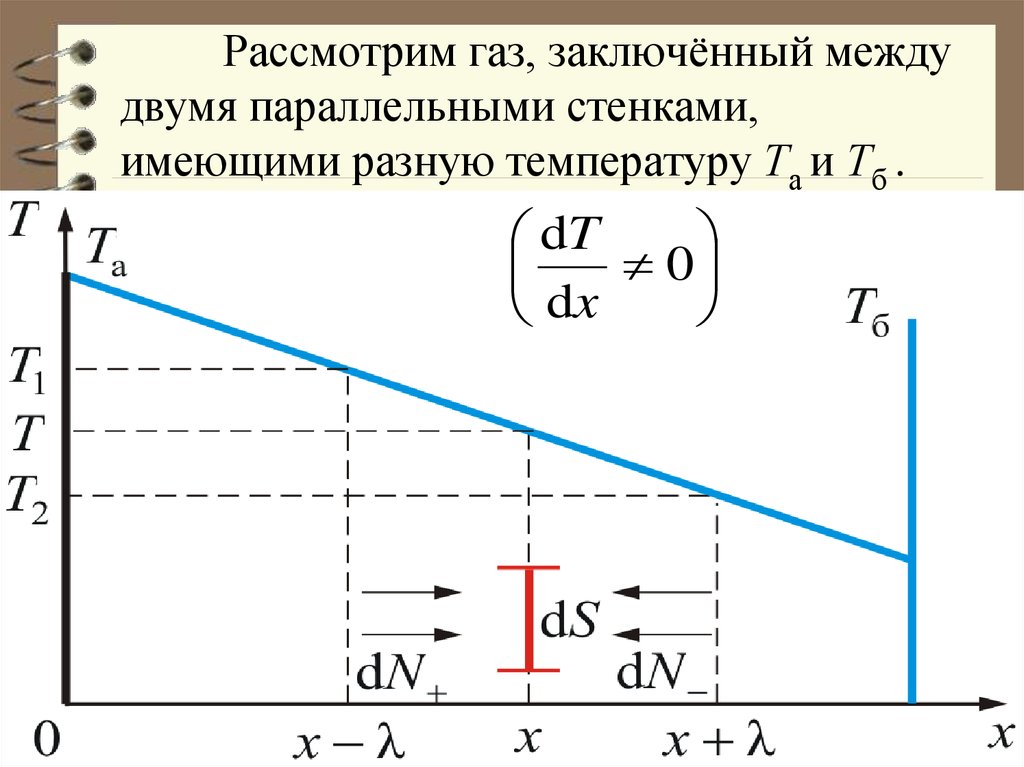
22. Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру Та и Тб .

dT
0
dx

23. Итак, у нас имеется градиент температуры Тогда через газ в направлении оси х будет идти поток тепла. Хаотично двигаясь,

Итак, у нас имеется градиент температуры
dT
0
dx
Тогда через газ в направлении оси х будет
идти поток тепла.
Хаотично двигаясь, молекулы будут
переходить из одного слоя газа в другой, перенося
с собой энергию. Это движение молекул приводит
к перемешиванию молекул, имеющих различную
кинетическую энергию :
m0
i
Е
kT
2
2
2
здесь i – число степеней свободы молекулы.

24.

При подсчёте потока тепла
введём следующие упрощения:
Среднеарифметическая
скорость теплового движения
молекул
υT const
Концентрация молекул в
соседних слоях одинакова, хотя на
самом деле она различается ( что
даёт ошибку 10 %).

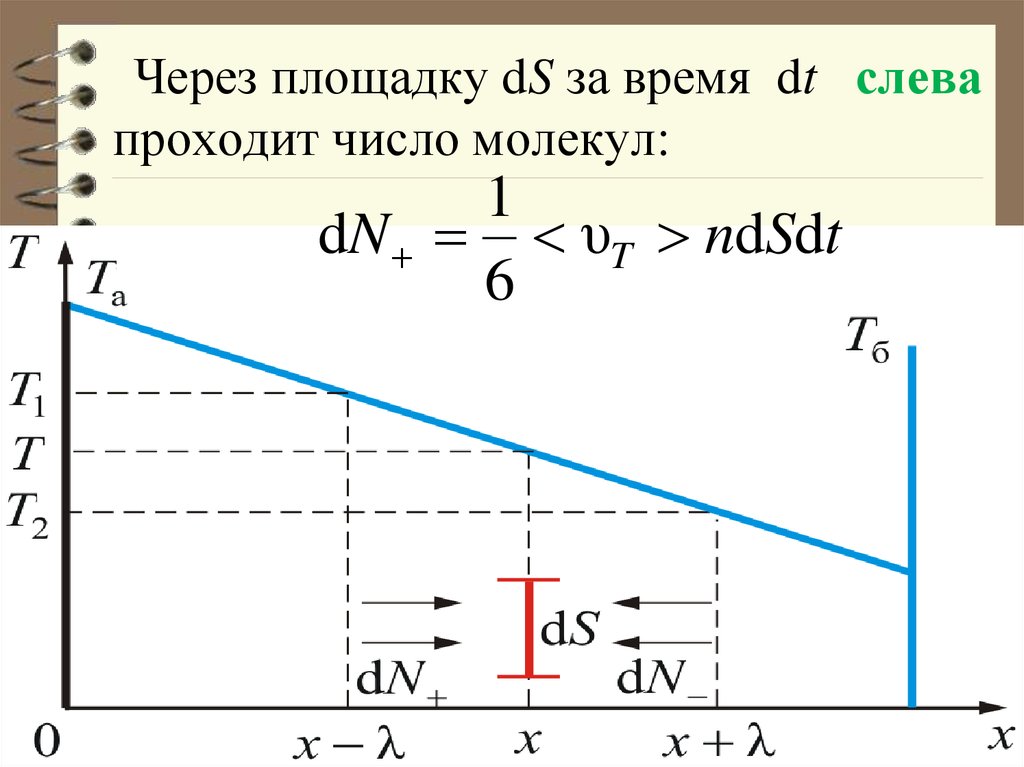
25. Через площадку dS за время dt слева проходит число молекул:

1
dN υT ndSdt
6

26. Средняя энергия этих молекул Е – соответствует значению энергии в том месте, где они испытывают последний раз столкновение. Для

одной молекулы газа:
i
Е1 kT1.
2
Соответственно, справа проходит
1
dN n υT dSdt
6
молекул.
Каждая из этих молекул перенесёт энергию
i
Е2 kT2 .
2

27. Результирующий поток энергии через dS равен разности потоков и , то есть Применяя те же рассуждения, получим: результирующий

Результирующий поток энергии через
dS равен разности потоков dQ и dQ , то есть
1
i
dQ n υT dSdt k (T1 T2 )
6
2
Применяя те же рассуждения, получим:
результирующий поток через единичную
площадку в единицу времени равен q и
направлен он в сторону противоположную
направлению градиента:
dQ
1
i dT
q λ υT n k
dSdt
3
2 dx ,
dT - закон Фурье
q χ
dx (одномерный вид)

28. или – уравнение теплопроводности Ж.Фурье. Здесь q – тепловой поток; χ – коэффициент теплопроводности, равный: или

или
q χ grad T
– уравнение теплопроводности
Ж.Фурье. Здесь q – тепловой поток;
χ – коэффициент теплопроводности,
равный:
1
i
χ λ υT n k
3
2 или
1
χ λ υT ρCVУД
3

29. υТ – тепловая скорость молекул; – удельная теплоемкость при постоянном объеме. Найдем размерность коэффициента

1
χ λ υT ρCVУД
3
υТ – тепловая скорость молекул;
CVуд – удельная теплоемкость при
постоянном объеме.
Найдем размерность коэффициента
теплопроводности:
qdx
Дж м
Вт
2
dT м К с м К

30.

31. Если какое либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже

Внутреннее трение.
Вязкость газов.
Если какое либо тело движется в газе,
то оно сталкивается с молекулами газа и
сообщает им импульс. С другой стороны,
тело тоже будет испытывать соударения со
стороны молекул, и получать собственный
импульс,
но
направленный
в
противоположную
сторону.
Газ
ускоряется, тело тормозиться, то есть, на
тело действуют силы трения.

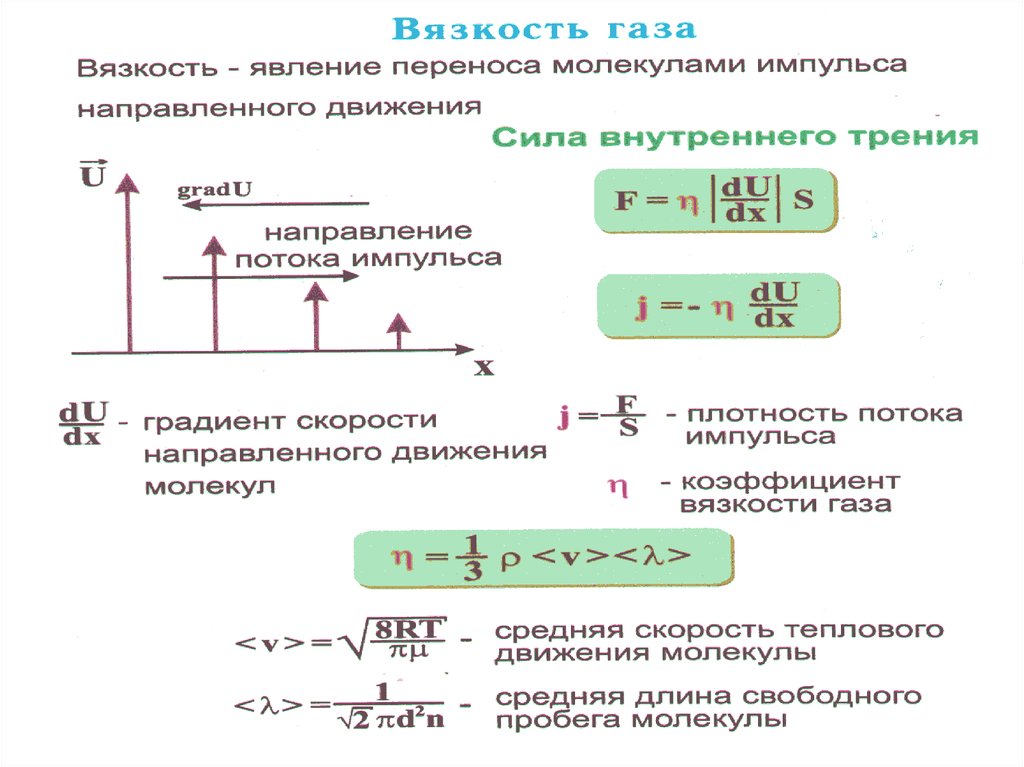
32. Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости:

Такая же сила трения будет действовать
и между двумя соседними слоями газа (или
жидкости), движущимися с разными
скоростями.
Это
явление
носит
название
внутреннее трение или вязкость газа,
причём сила трения пропорциональна
градиенту
скорости:
dυ
Fтр ~
dx

33.

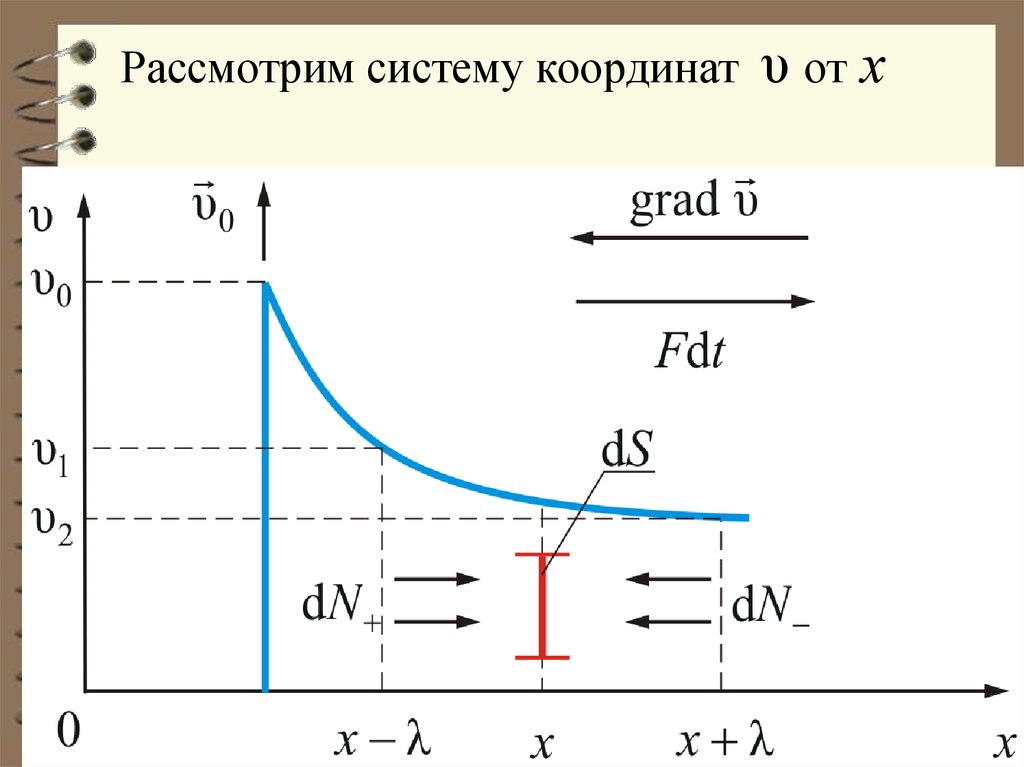
Рассмотрим систему координат
υ от х

34. Пусть в покоящемся газе вверх, перпендикулярно оси х движется пластинка со скоростью υ0, причём (υT – скорость теплового

Пусть в покоящемся газе вверх,
перпендикулярно оси х движется пластинка
со скоростью υ0, причём υ0 υT
(υT – скорость теплового движения
молекул). Пластинка увлекает за собой
прилегающий слой газа, тот соседний слой
и так далее. Весь газ делится, как бы на
тончайшие слои, скользящие вверх тем
медленнее, чем дальше они от пластинки.
Раз слои газа движутся с разными
скоростями, возникает трение.
Выясним причину трения в газе.

35. Каждая молекула газа в слое принимает участие в двух движениях: тепловом и направленном. Так как направление теплового движения

хаотически меняется, то в
среднем вектор тепловой скорости
равен нулю
υT 0
При направленном движении вся
совокупность молекул будет
дрейфовать с постоянной скоростью υ.

36. Средний импульс отдельной молекулы в слое определяется только дрейфовой скоростью υ: Но так как молекулы участвуют в тепловом

Средний импульс отдельной молекулы в слое
определяется только дрейфовой скоростью υ:
p0 m0 υ.
Но так как молекулы участвуют в тепловом
движении, они будут переходить из слоя в слой.
При этом они будут переносить с собой добавочный импульс, который будет определяться
молекулами того слоя, куда перешла молекула.
Перемешивание молекул разных слоёв
приводит к выравниванию дрейфовых
скоростей разных слоёв, что и проявляется
макроскопически как действие сил трения
между слоями.

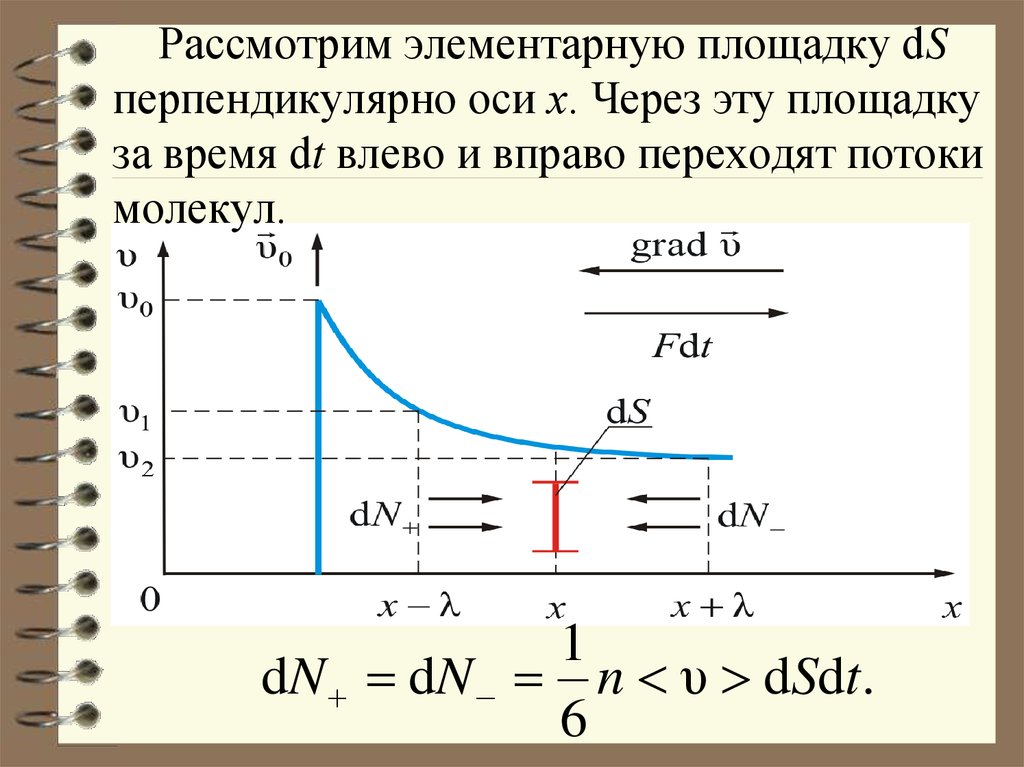
37. Рассмотрим элементарную площадку dS перпендикулярно оси х. Через эту площадку за время dt влево и вправо переходят потоки

молекул.
1
dN dN n υ dSdt.
6

38. Но эти потоки переносят разный импульс: и При переносе импульса от слоя к слою происходит изменение импульса этих слоёв. Это

Но эти потоки переносят разный
m0 υ 2dN
импульс: m0 υ1dN
и
При переносе импульса от слоя к
слою происходит изменение импульса
этих слоёв. Это значит, что на каждый из
этих слоёв действует сила, равная
изменению импульса.
Сила эта есть не что иное, как сила
трения между слоями газа, движущимися с различными скоростями. Отсюда и
название – внутреннее трение.

39. Закон вязкости был открыт И. Ньютоном в 1687 г. Переносимый за время dt импульс равен: или Отсюда получим силу, действующую на

Закон вязкости был открыт И.
Ньютоном в 1687 г.
Переносимый за время dt импульс
равен: d(m0 υ)
или
1
Fdt n υ m0 ( υ1 υ 2 )dS
6
Отсюда получим силу, действующую
на единицу площади поверхности,
разделяющей два соседних слоя газа:
F
1
υ 2 υ1
υ1 υ 2 1
f υ nm0
m0 n
dS
3
2
2 3

40. Сила, действующая на единицу площади поверхности, разделяющей два соседних слоя газа: - уравнение Ньютона Или, в общем виде:

Сила, действующая на единицу площади
поверхности, разделяющей два соседних
слоя газа:
d
f
- уравнение Ньютона
dx
Или, в общем виде:
f grad
уравнение Ньютона.
Здесь η – коэффициент вязкости:
1
1
υ nm0 υ D
3
3
где D – коэффициент диффузии;
ρ – плотность газа.

41. Физический смысл коэффици-ента вязкости η в том, что он численно равен импульсу, переносимому в единицу времени через единицу

1
- коэффициент
υ
вязкости
3
Физический смысл коэффициента вязкости η в том, что он
численно равен импульсу,
переносимому в единицу времени
через единицу площади при градиенте
скорости равном единице.

42.

43. Уравнения и коэффициенты переноса

Сопоставим уравнения переноса
J Dgrad n
dn
J D
dx
Уравнение Фика для диффузии.
1
Коэффициент диффузии D λ υT
3

44. или Уравнение Фурье для теплопроводности. Коэффициент теплопроводности:

q χ gradT
или
dT
q χ
dx
Уравнение Фурье
для теплопроводности.
Коэффициент теплопроводности:
1
χ λ υT ρCуд DρCуд
3

45.

f тр η grad υ
dυ
f тр
dx
- Уравнение Ньютона
для трения.
Коэффициент вязкости:
1
υT D
3