Процессы переноса

1.

ЛЕКЦИЯ 14
ПРОЦЕССЫ ПЕРЕНОСА
1. Диффузия газов. Закон Фика. Коэффициент
диффузии.
2. Теплопроводность газов. Уравнение Фурье.
Коэффициент теплопроводности.
3. Внутреннее трение. Уравнение Ньютона.
Коэффициент вязкости.
4. Сильно неравновесные открытые системы и
процессы

2.

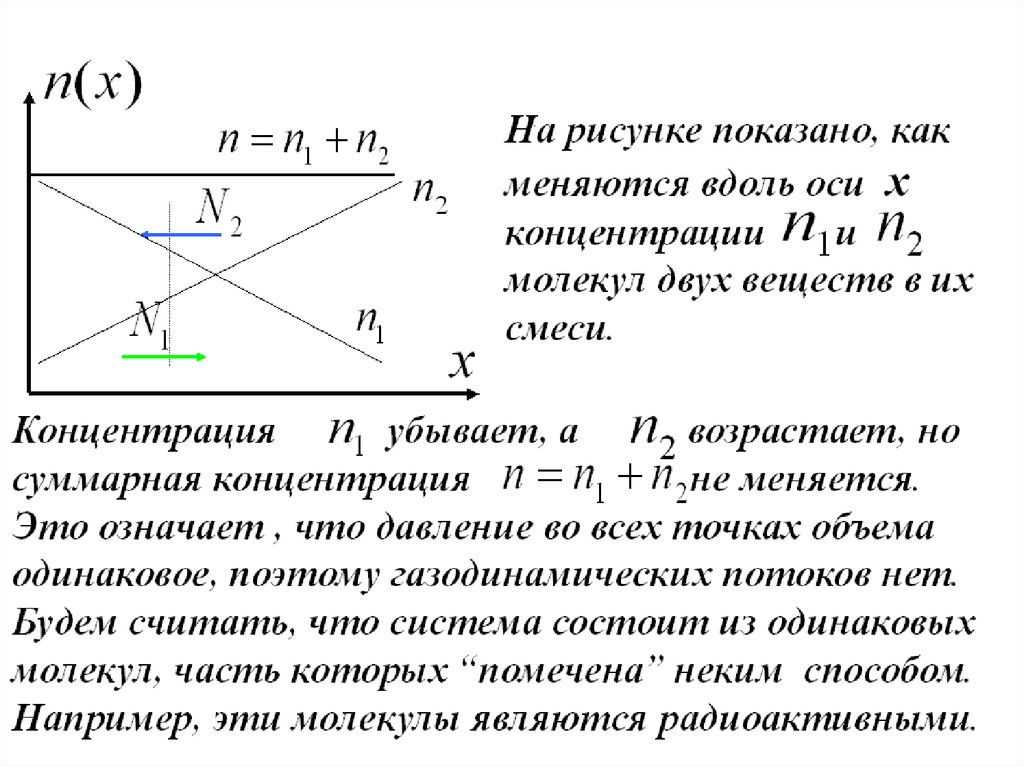
Процессы переноса
При нарушении равновесия в системе возникают процессы переноса энергии (теплопроводность), вещества
(диффузия) или импульса (вязкое трение). Все эти процессы являются необратимыми, так как обусловлены
хаотическим тепловым движением молекул .
Диффузия газов
Диффузия от латинского diffusio –
распространение, растекание взаимное
проникновение соприкасающихся веществ друг в друга,
вследствие теплового движения частиц вещества.
Диффузия происходит в направлении уменьшения
концентрации вещества и ведет к его равномерному
распределению по занимаемому объему.

3.

26.01.2019

4.

26.01.2019

5.

Физический смысл знака “ – “ в этом уравнении:
поток диффузии всегда направлен в сторону
dn
убывания концентрации
получаем
0(при
Jx 0
dx
).
Найдем коэффициент диффузии.
Рассмотрим кубик единичного объема. В нем содержится n одинаковых молекул, которые движутся
хаотично.
Для упрощения будем
предполагать, что в каждом
y 1 6n
из направлений:
+x; -x
1 6n
1 6n
+y; -y
x
+z; -z
z
движется 1 6 n молекул.
1 6n

6.

Поток частиц J : это число молекул,
проходящих через площадку S единичной площади,
перпендикулярную к их скорости, за единицу времени.
Возьмем площадку S в качестве основания
параллепипеда с высотой равной v . Все молекулы,
находящиеся в нем, пролетят через S за 1с. Объем
пар-да численно равен v .Тогда
n
v
S 1
J n v
v
где
n
v
- концентрация молекул;
- средняя скорость теплового движения.

7.

Так как 10 м - очень маленькая величина, то
концентрации n( x ) и n( x ) можно
представить следующим образом:
7
dn
dn
n( x ) n( x ) ; n( x ) n( x ) ;
dx
dx
1
dn
1
dn
J x v [ n( x ) ] v [ n( x ) ]
6
dx
6
dx
1
dn
Jx v
3
dx

8.

Из сравнения выражений:
dn
J x D
dx
1
dn
Jx v
3
dx
находим коэффициент диффузии
D
1
D v
3
Зависимость
D от давления и температуры.
1 8kT
1
1 (kT )3
D
~
3 m0 2 n p
m0
D ~1 p
при T = const и
D~T
3
2
при p = const

9.

Теплопроводность. Закон Фурье.
Если различные части системы имеют разные
температуры (газ неравномерно нагрет), то возникает поток тепла от более нагретой части газа к менее
нагретой. Это явление называют
теплопроводностью.
В реальных процессах T(t) – нестационарный
процесс. Математически легче описать стационарный процесс, когда разность температур не меняется
со временем.
Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру
Та и Тб

10.

Направление
потока тепла
Температура убывает вдоль оси x, то есть
существует градиент температуры dT
0
dx

11.

Экспериментально полученный закон Фурье
показывает, что поток тепла Q через единичную
площадку, перпендикулярную направлению потока,
равен
dT
Q
dx
где - коэффициент теплопроводности. Знак «-»
означает, что поток тепла направлен в сторону
dT
убывания температуры:
Q 0 при
dx
0
Найдем коэффициент теплопроводности .
Рассмотрим поток тепла через площадку dS
единичной площади, расположенную перпендикулярно к направлению потока, за единицу времени.

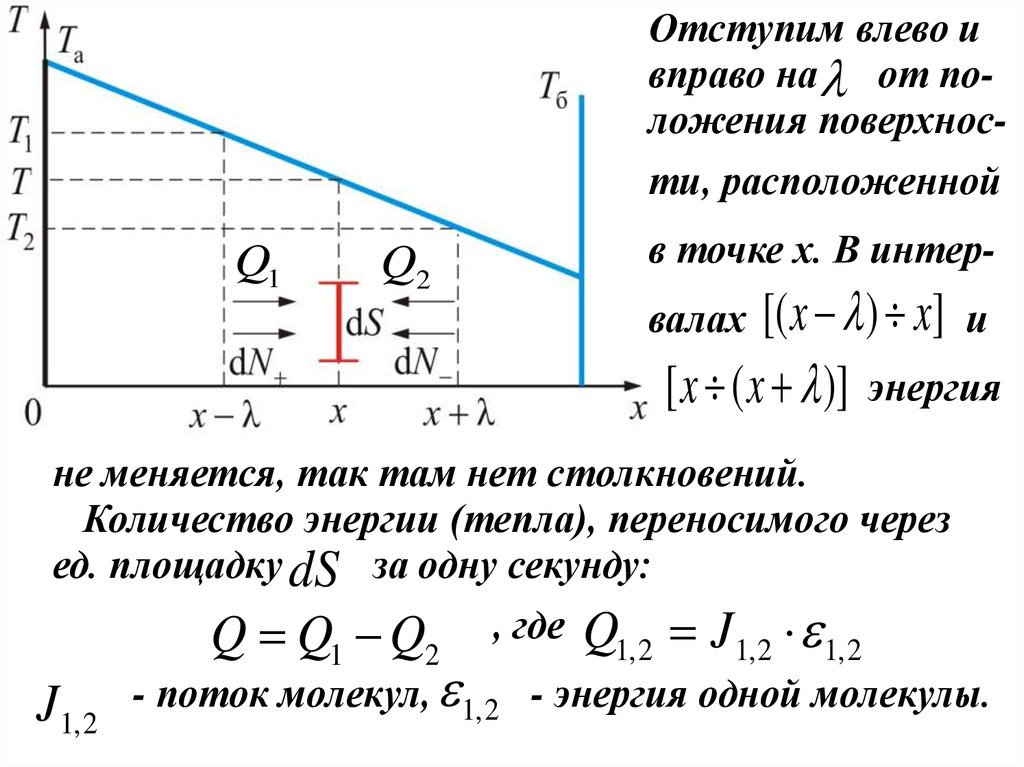
12.

Отступим влево и
вправо на от положения поверхности, расположенной
Q1
Q2
в точке x. В интер-
[( x ) x] и
[ x ( x )] энергия
валах
не меняется, так там нет столкновений.
Количество энергии (тепла), переносимого через
ед. площадку dS за одну секунду:
J1, 2
Q Q1 Q2 , где Q1, 2 J1, 2 1, 2
- поток молекул, 1, 2 - энергия одной молекулы.

13.

Q1
Q2
1
Q1 n v 1 ;
6
1
Q2 n v 2
6
1
Q n v ( 1 2 )
6
Энергия одной молекулы
CV
i
i kN A
iR 1
kT
T
T
T
2
2 NA
2 NA
NA

14.

Так как CV cV , где CV - молярная теплоемкость при V=const, а cV - удельная теплоемкость, то
где
Тогда
CV
T
cV T m0 cV T
NA
NA
m0 - масса одной молекулы.
dT
1 m0 cV T1 ( x ) m0 cV T ( x)
dx
dT
2 m0 cV T2 ( x ) m0 cV T ( x)
dx
dT
1 2 2m0 cV
dx

15.

Окончательно
1
dT
Q m0 n v cV
3
dx
Сравнивая с законом Фурье Q dT , получаем
dx
выражение для коэффициента теплопроводности
1
1
m0 n v cV v cV
3
3

16.

Зависимость
от давления и температуры.
1
1
m0 n v cV v cV
3
3
Подставим значения
8kT
1
и v
m0
2 n
1
8kT
1
2 m0 cV kT
m0 n
cV
3
m0 2 n
3
m0
Из полученного выражения можно сделать вывод, что
не зависит от давления (р). Однако это справедливо, когда L . L - расстояние между пластинами с
разной температурой. Если L (термос, сосуд
Дьюара),
~n~ p .

17.

Внутреннее трение. Вязкость газов
Вязкость газов (жидкостей) – это свойство, благодаря которому выравниваются скорости движения
различных слоев газа. В природе это приводит к
стиханию бурь, смерчей, торнадо.
Пусть в покоящемся газе вдоль оси х движется
пластинка со скоростью u , причём u ( v )
( v – средняя скорость теплового движения
молекул). Пластинка увлекает за собой прилегающий
слой газа, тот увлекает соседний
u
слой и так далее. Весь газ делится на тонкие слои, скользящие
тем медленнее, чем дальше они
от движущейся пластинки.
Вторая пластинка неподвижна.

18.

x
Раз слои газа движутся
с разными скоростями,
u
возникает трение.
u Выясним причину
трения в газе.
2 u 2
v
Каждая молекула газа в
1 u1
слое принимает
участие в двух
z движениях: тепловом
(хаотическом) и
направленном (упорядоченном). Так как направление
теплового движения хаотически меняется, то в
среднем вектор тепловой скорости равен нулю. При
направленном движении все молекулы в слое будут
дрейфовать с постоянной для слоя скоростью u .
z

19.

Средний импульс отдельной молекулы в слое
определяется только дрейфовой скоростью слоя
p0 m0u
u
Но так как молекулы участвуют в тепловом
движении, они будут переходить из слоя в слой. При
этом они будут переносить с собой импульс
упорядоченного движения, что будет приводить к
изменению импульсов обоих слоев. В примере на
рисунке при переходе молекул из слоя 1 в слой 2
суммарный импульс упорядоченного движения слоя 2
уменьшается так как m0u1 m0u 2 Переход
молекул из слоя 2 в слой 1 приводит к увеличению
суммарного импульса упорядоченного движения слоя
1.

20.

Обозначим импульс слоя 1 - p1, слоя 2 ное запишем математически:
dp2
0
dt
dp1
0,
dt
По 2-ому закону Ньютона
Следовательно,
dp1
Fтр1 0
dt
x
u
Fтр1
;
Fтр2
z
p2 . Сказан-
dp
F.
dt
dp2
;
Fтр1 Fтр2
Fтр 2 0
dt
Fтр1 и Fтр2 - силы трения между
слоями газа, движущимися с
разными скоростями. Отсюда и
название – внутреннее трение.

21.

Закон вязкости был открыт И. Ньютоном в 1687 г:
Импульс, переносимый за 1с через площадку единичной
площади, перпендикулярную направлению переноса ,
равен:
du
F
dx
где
F Fтр
- коэффициент вязкости
du
dx
- градиент скорости упорядоченного движения
Рассчитаем коэффициент вязкости.

22.

Коэффициент вязкости.
u
Импульс одной молекулы
u( x )
S
J1
x
x
J2
u( x )
x
чертеж повернут на 900
p0 m0u
Поток импульса упорядоченного движения
через единичную плоx щадку S за единицу
времени:
J1m0u ( x ) J 2 m0u ( x )
1
1
n v m0u ( x ) n v m0u ( x )
6
6

23.

du
Так как u ( x ) u ( x )
;
dx
du
u ( x ) u ( x) ;
dx
1
du
du
F m0 n v ([u ( x) ] [u ( x) ])
6
dx
dx
1
du
F m0 n v
3
dx
Коэффициент вязкости
1
m0 n v
3

24.

Зависимость
от давления и температуры
1
1
m0 n v v
3
3
Подставим значения
1
8kT
и v
m0
2 n
1
8kT
1
2 m0 kT
m0 n
3
m0 2 n 3 m0
Из полученного выражение можно сделать вывод, что
не зависит от давления (р), но зависит от
температуры
12
~T

25.

СИЛЬНО НЕРАВНОВЕСНЫЕ ОТКРЫТЫЕ СИСТЕМЫ
И ПРОЦЕССЫ САМООРГАНИЗАЦИИ
Любая закрытая система стремится к состоянию
термодинамического равновесия, при этом ее энтропия
стремится к максимуму (беспорядок и хаос нарастает).
На основании этого Клаузиус выдвинул гипотезу о
тепловой смерти Вселенной. Но закрытые системы —
это идеализация. Все наблюдаемые системы во
Вселенной — открытые. Во многих сферах вместо
нарастания хаоса мы наблюдаем эволюционные
процессы приводящие к упорядочению и усложнению
организации. Такие процессы рассматривает
термодинамика открытых систем.
Это системы, обменивающиеся с окружающей средой
веществом, энергией или информацией.

26.

Открытая система тоже производит энтропию, как и
закрытая, но в отличие от закрытой эта энтропия не
накапливается в открытой системе, а выводится в
окружающую среду. Использованная энергия рассеивается в окружающей среде и взамен ее из среды извлекается новая энергия (порядок), способная производить
новые структуры. В результате такого взаимодействия
система извлекает упорядоченное вещество, энергию
или информацию из окружающей среды, одновременно
внося туда беспорядок. С поступлением новой энергии,
вещества или информации неравновесность в системе
возрастает. Прежняя взаимосвязь между элементами
системы, которая определяла ее структуру, разрушается. Между элементами системы возникают новые
связи, приводящие к кооперативным процессам, то есть
к коллективному поведению элементов. Так схематически можно описать процессы самоорганизации.

27.

Необходимыми условиями для возникновения
самоорганизации в системах являются следующие:
система должна быть открытой, потому что
закрытая система, в конечном счете, должна прийти в
состояние максимального беспорядка, хаоса,
дезорганизации;
открытая система должна находиться достаточно
далеко от точки термодинамического равновесия. Если
система расположена вблизи от точки
термодинамического равновесия, то со временем она
неизбежно приблизится к ней и, в конце концов, придет
в состояние полного хаоса;
фундаментальным принципом самоорганизации
служит возникновение порядка через флуктуации.
Флуктуации или случайные отклонения системы от

28.

среднего положения в открытых системах благодаря
неравновесности со временем возрастают и, в конце
концов, приводят к “расшатыванию” прежнего
порядка и возникновению нового. Этот процесс
характеризуется как принцип образования порядка
через флуктуации.
Возникновение самоорганизации опирается на
положительную обратную связь. Согласно принципу
положительной обратной связи, изменения
появляющиеся в системе не устраняются, а
усиливаются, накапливаются, что приводит, в конце
концов, к возникновению нового порядка и структуры.
Самоорганизация может начаться лишь при
достижении системой некоторых критических
параметров. Для каждой самоорганизующейся
системы эти критические параметры свои.