Similar presentations:
Молекулярно-кинетическая теория. Тема 4
1. Тема 4. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
Тема 4. МОЛЕКУЛЯРНОКИНЕТИЧЕСКАЯ ТЕОРИЯ4.1. Основные понятия и определения молекулярной физики и
термодинамики
4.2. Давление. Основное уравнение молекулярно-кинетической теории
4.3. Температура и средняя кинетическая энергия теплового движения
молекул
4.4. Законы идеальных газов
4.5. Уравнение состояния идеального газа (уравнение МенделееваКлапейрона)
4.6. Явления переноса в газах
4.7. Число столкновений и средняя длина свободного пробега молекул
в газах
4.8. Диффузия газов
4.9. Внутреннее трение. Вязкость газов
4.10. Теплопроводность газов
4.11. Коэффициенты переноса и их зависимость от давления
4.12. Внутренняя энергия. Работа и теплота
4.13. Применение первого начала
термодинамики к изопроцессам
идеальных газов
2. 4.1. Основные понятия и определения молекулярной физики и термодинамики
• Совокупностьтел,
составляющих
макроскопическую
систему,
называется
термодинамической системой.
• Система может находиться в различных
состояниях. Величины, характеризующие
состояние
системы,
называются
параметрами
состояния:
давление
P,
температура T, объём V и так далее. Связь
между P, T, V специфична для каждого тела и
называется уравнением состояния.
3. Любой параметр, имеющий определённое значение для каждого равновесного состояния, является функцией состояния системы.
Равновесная система - такаясистема, параметры состояния которой
одинаковы во всех точках системы и не
изменяются со временем (при неизменных
внешних условиях). При этом в равновесии
находятся отдельные, макроскопические
части системы.
4. Процесс – переход из одного равновесного состояния в другое. Релаксация – возвращение системы в равновесное состояние. Время
перехода – время релаксации.5. Если равновесие установилось, то система самопроизвольно не сможет выйти из него. Например, если опустить горячий камень в
холодную воду, то, через некотороевремя наступит равновесное состояние:
температуры выровняются. Но обратный
процесс невозможен – температура камня
самопроизвольно не увеличится.
6. Атомная единица массы (а.е.м.) – (mед) – единица массы, равная 1/12 массы изотопа углерода С12 – mC: Атомная масса химического
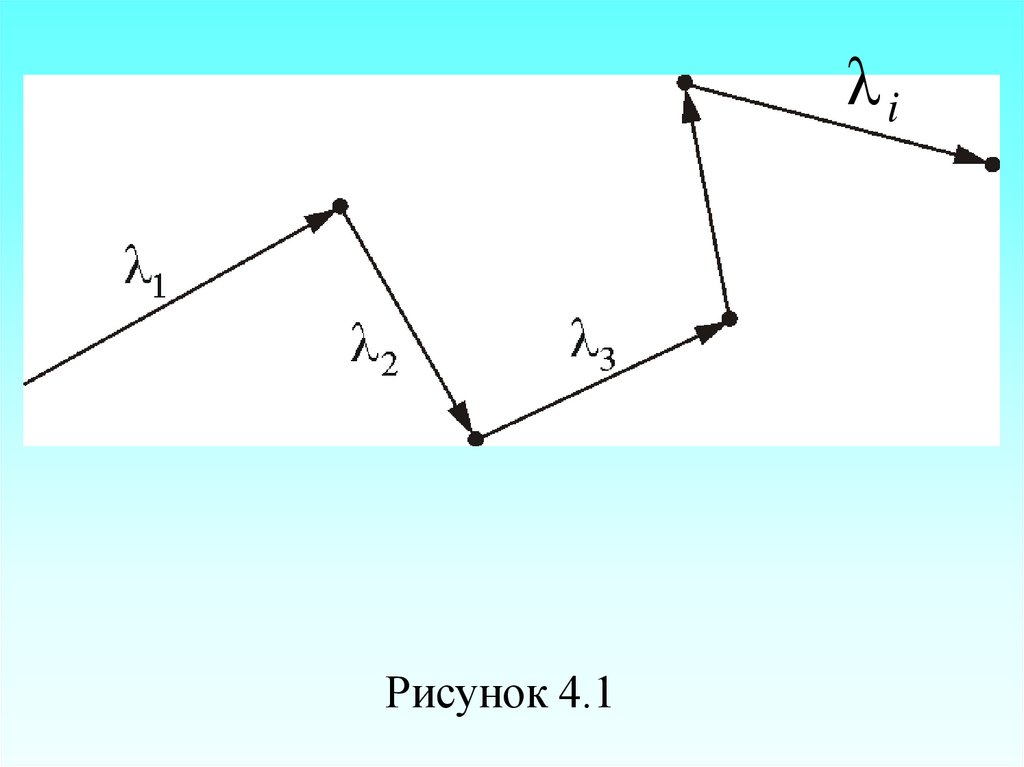
Атомная единица массы (а.е.м.) –(mед) – единица массы, равная 1/12
массы изотопа углерода С12 – mC:
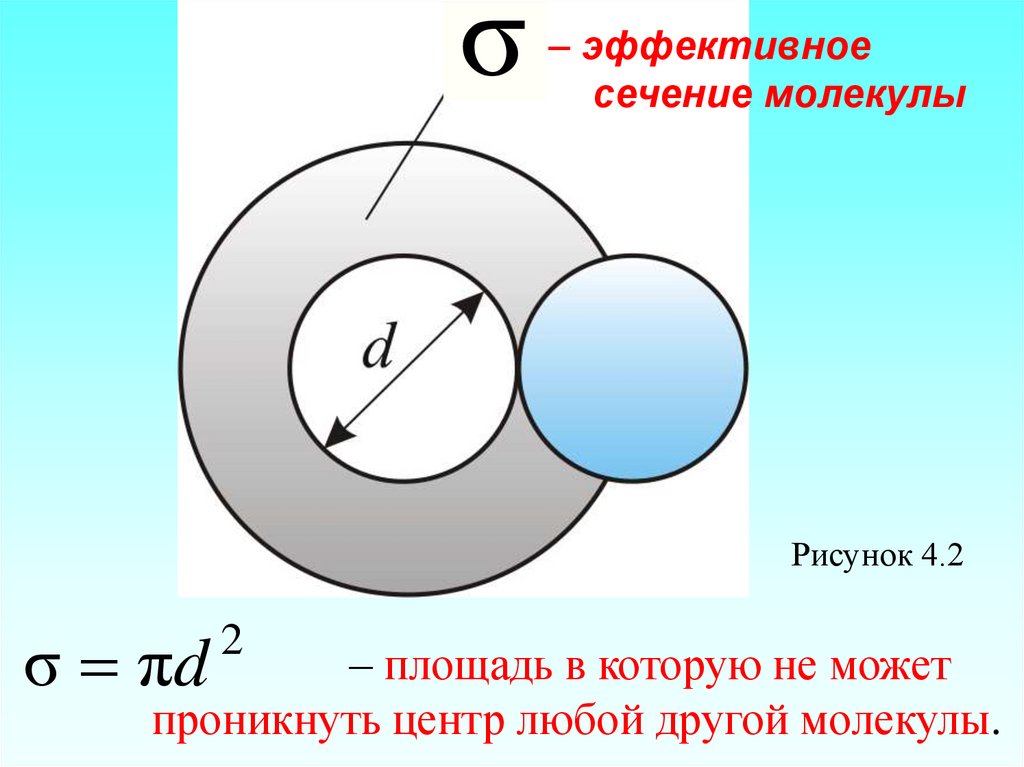
mед (1/ 12)mC 1,66 10
27
кг.
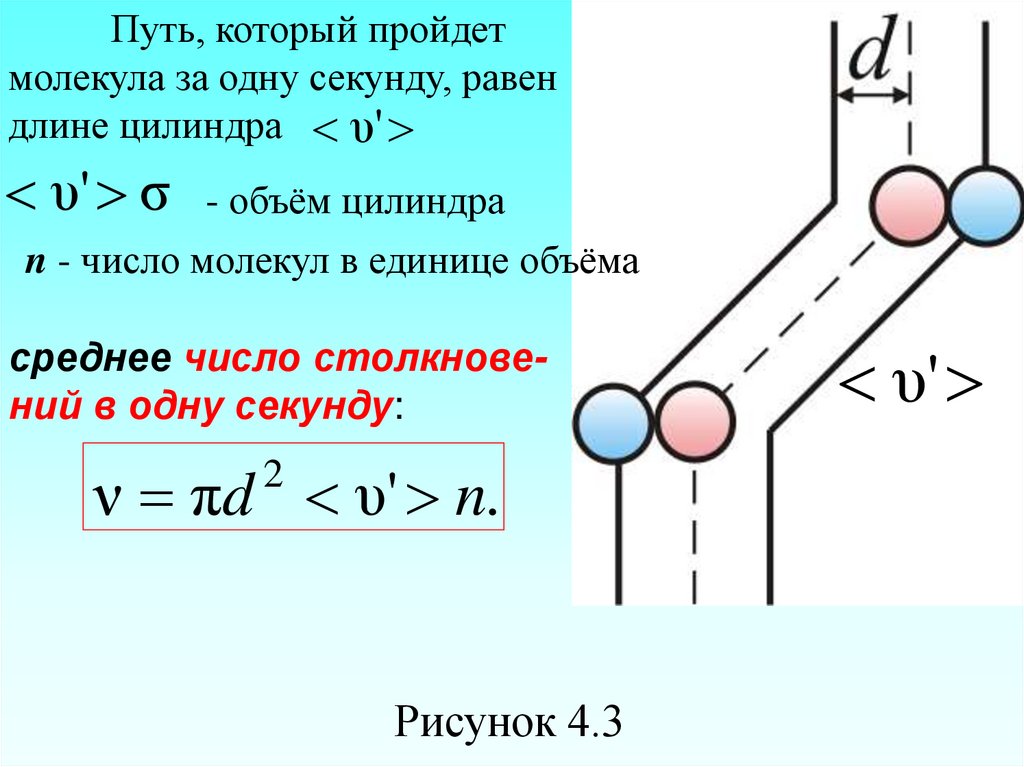
Атомная масса химического элемента
(атомный вес) А, есть отношение массы
атома этого элемента mA к 1/12 массы
изотопа углерода С12
(атомная масса – безразмерная величина).
7. Молекулярная масса (молекулярный вес): Отсюда можно найти массу атома и молекулы в килограммах:
Молекулярная масса (молекулярныйвес):
mM масса молекулы
M
.
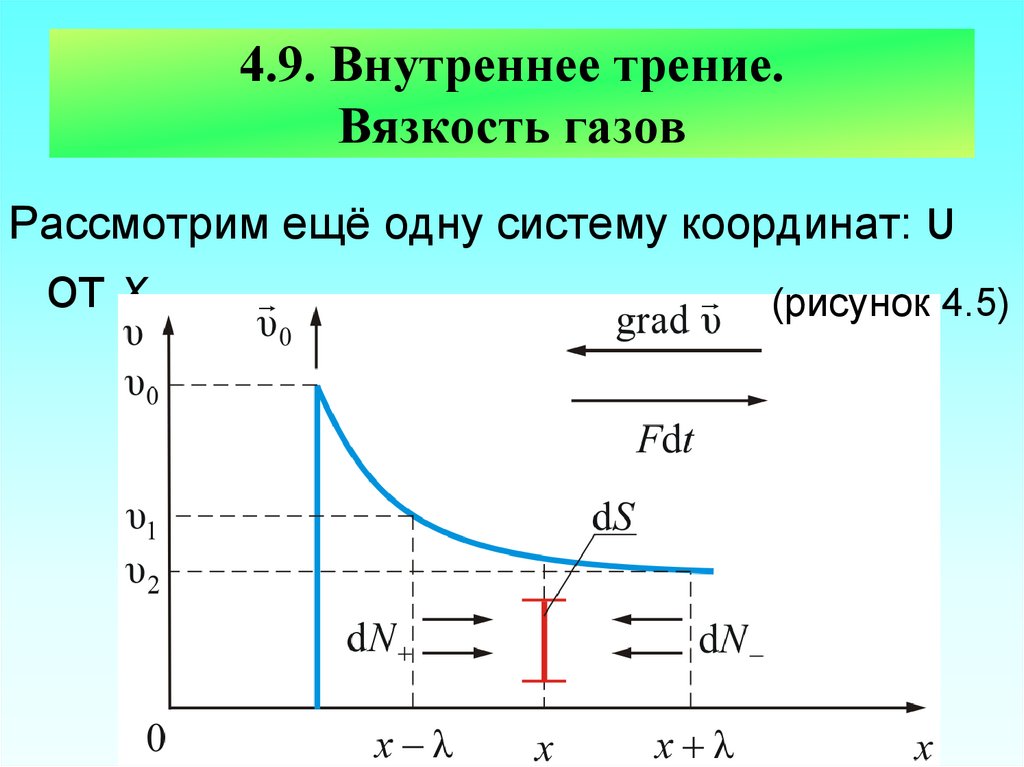
mед
Отсюда можно найти массу атома и
молекулы в килограммах:
mA Amед
mM Mmед
8. В термодинамике широко используют понятия киломоль, моль, число Авогадро и число Лошмидта. Дадим определения этих величин. Моль
– это стандартизированноеколичество любого вещества, находящегося
в газообразном, жидком или твердом
состоянии.
1 моль – это количество грамм
вещества, равное его молекулярной массе.
9. 1 киломоль - это количество килограмм вещества, равное его молекулярной массе.
1 моль – количество грамм вещества,равное его молекулярной массе.
1 киломоль - это количество
килограмм вещества, равное его
молекулярной массе.
μ кг/кмоль г/моль М или А (безразмерн .)
10. В 1811 г. Авогадро высказал предположение, что число частиц в киломоле любого вещества постоянно и равно величине, названной, в
последствии, числом Авогадроμ г/моль
1
1
23
NA
6,022 10
.
M mед г mед
моль
1
N A 6,022 10
.
моль
23
Молярная масса – масса одного моля (µ)
μ Amед N A.
11. При одинаковых температурах и давлениях все газы содержат в единице объёма одинаковое число молекул. Число молекул идеального
газа,содержащихся в 1 м3 при нормальных
условиях, называется числом Лошмидта:
N L P0 / kT0 2,68 10
25
м
3
Нормальные условия: P0 = 105 Па; Т0 = 273 К;
k = 1,38·10 23 Дж/К – постоянная Больцмана
12.
k = 1,38·10 23 Дж/К – постоянная Больцмана13. Под идеальным газом мы будем понимать газ, для которого: 1) радиус взаимодействия двух молекул много меньше среднего расстояния
междуними (молекулы взаимодействуют только
при столкновении);
2) столкновения молекул между собой и со
стенками сосуда – абсолютно упругие
(выполняются законы сохранения энергии и
импульса);
3) объем всех молекул газа много
меньше объема, занятого газом.
14. 4.2. Давление. Основное уравнение молекулярно-кинетической теории
Рассмотрим подробнее, что представляетсобой один из основных параметров
состояния – давление P.
Ещё в XVIII веке Даниил Бернулли
предположил, что давление газа – есть
следствие столкновения газовых
молекул со стенками сосуда.
Именно давление чаще всего является
единственным сигналом присутствия газа.
15. Итак, находящиеся под давлением газ или жидкость действуют с некоторой силой на любую поверхность, ограничивающую их объем. В
этом случае сила действует понормали к ограничивающей объем
поверхности. Давление на поверхность
равно:
ΔF
P
ΔS
где ΔF – сила, действующая на поверхность
площадью ΔS.
16. Внутреннее давление является одним и тем же во всех направлениях, и, во всем объеме независимо от формы сосуда. Этот результат
называется закономПаскаля: если к некоторой части
поверхности, ограничивающей газ или
жидкость, приложено давление P0, то
оно одинаково передается любой части
этой поверхности.
17. Таким образом, мы определили давление, как силу, действующую в единицу времени на единицу площади: (4.2.2)
P dF / dS.или
1
2
P m0 υ x
3
18.
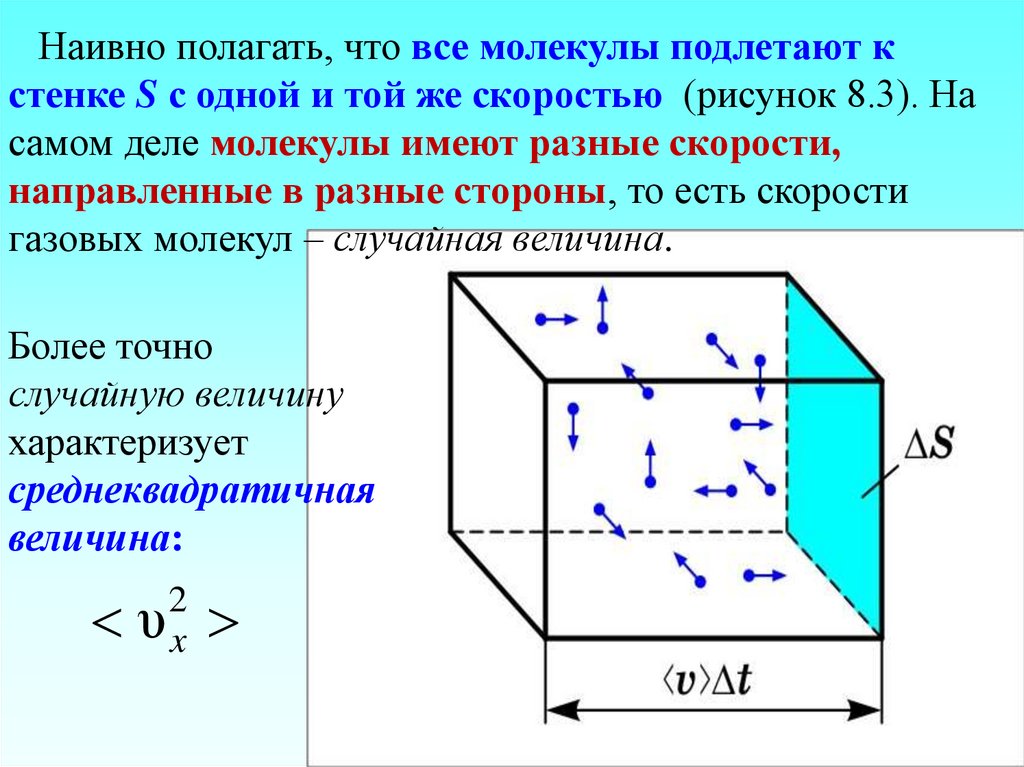
Наивно полагать, что все молекулы подлетают кстенке S с одной и той же скоростью (рисунок 8.3). На
самом деле молекулы имеют разные скорости,
направленные в разные стороны, то есть скорости
газовых молекул – случайная величина.
Более точно
случайную величину
характеризует
среднеквадратичная
величина:
2
υx
19. Под скоростью понимаем среднеквадратичную скорость Вектор скорости, направленный произвольно в пространстве, можно разделить на
2Под скоростью υ x
понимаем
2
среднеквадратичную скорость υ x
Вектор скорости, направленный
произвольно в пространстве, можно разделить
на три составляющих:
υ
2
2
2
2
υ x υ y υ z .
Ни одной из этих проекций нельзя отдать
предпочтение из-за хаотичного теплового
движения молекул, то есть в среднем
2
2
2
υx υ y υz
.
20. Следовательно, на другие стенки будет точно такое же давление. Тогда можно записать в общем случае: или (4.2.3) где – средняя
Следовательно, на другие стенки будет точнотакое же давление. Тогда можно записать в общем
случае:
2
или
1
2 m0 υ
2
P m0 n υ n
,
3
3
2
2
P n Ek
3
(4.2.3)
где E k – средняя энергия одной молекулы.
Это основное уравнение молекулярно-
кинетической теории газов.
Итак, давление газов определяется средней
кинетической энергией поступательного
движения молекул.
21. Единицы измерения давления. По определению, поэтому размерность давления 1 Н/м2 = 1Па; 1 атм.= 9,8 Н/см2 = 98066 Па 105 Па 1
Единицы измерения давления.F
По определению, P , поэтому
S
размерность давления
Н
.
2
м
1 Н/м2 = 1Па;
1 атм.= 9,8 Н/см2 = 98066 Па 105 Па
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па
1 бар = 105 Па;
1 атм. = 0,98 бар.
22. 4.3. Температура и средняя кинетическая энергия теплового движения молекул
Из опыта известно, что если привести всоприкосновение два тела: горячее и холодное, то
через некоторое время их температуры
выровняются. Что перешло от одного тела к
другому?
Раньше, во времена Ломоносова и Лавуазье
считали, что носителем тепла является некоторая
жидкость – теплород.
На самом деле – ничего не переходит, только
изменяется средняя кинетическая энергия –
энергия движения молекул, из которых состоят эти
тела.
23. Именно средняя кинетическая энергия атомов и молекул служит характеристикой системы в состоянии равновесия. Это свойство
позволяет определитьпараметр состояния, выравнивающийся
у всех тел, контактирующих между собой,
как величину, пропорциональную
средней кинетической энергии частиц в
сосуде.
24. Чтобы связать энергию с температурой, Больцман ввел коэффициент пропор- циональности k, который впоследствии был назван его
Чтобы связать энергию стемпературой, Больцман
ввел коэффициент пропорциональности k, который
впоследствии был назван
его именем:
2 m0 υ
T
3k
2
2
где k – постоянная Больцмана
k = 1,38·10 23 Дж·К 1.
25. Величину T называют абсолютной темпе-ратурой и измеряют в градусах Кельвина (К). Она служит мерой кинетической энергии
Величину T называют абсолютной температурой и измеряют в градусах Кельвина (К). Онаслужит мерой кинетической энергии теплового
движения частиц идеального газа. Из (8.3.1)
получим:
m0 υ
2
2
3
kT .
2
Формула (8.3.2) применима для расчетов на
одну молекулу идеального газа.
Обозначим R kNA ,
где R – универсальная газовая постоянная:
Дж
Дж
3
R 8,31
8,31 10
моль K
кмоль К
26. В физике и технике за абсолютную шкалу температур принята шкала Кельвина, названная в честь знаменитого английского физика,
лорда Кельвина.1 К – одна из основных единиц системы СИ
Кроме того, используются и другие шкалы:
– шкала Фаренгейта (немецкий физик 1724 г.) –
точка таянья льда 32 F, точка кипения воды 212 F.
– шкала Цельсия (шведский физик 1842г.) – точка
таянья льда 0 С, точка кипения воды 100 С.
0 С = 273,15 К.
На рис.1.5приведено сравнение разных темп. шкал.
27. 4.4. Законы идеальных газов
В XVII – XIX веках былисформулированы опытные законы
идеальных газов, которые подробно
изучаются в школьном курсе физики.
Кратко напомним их.
Изопроцессы идеального газа –
процессы, при которых один из
параметров остаётся неизменным.
28. 1.Изохорический процесс. V = const. Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение
газа при этом изохорическомпроцессе подчиняется закону Шарля:
P/Т = const:
«При постоянном объёме и
неизменных значениях массы газа и его
молярной массы, отношение давления
газа к его абсолютной температуре
остаётся постоянным».
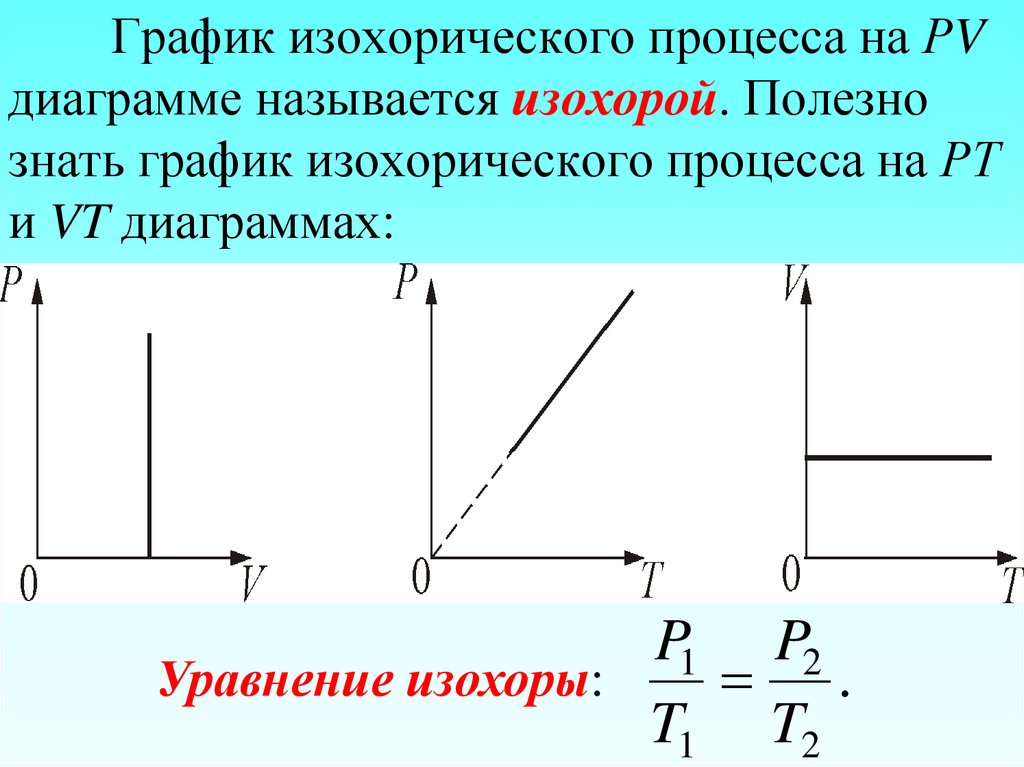
29. График изохорического процесса на РV диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ и VT
диаграммах:P1 P2
Уравнение изохоры:
.
T1 T2
30. Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде (4.4.2) где Р0 –
Если температура газа выражена в градусахЦельсия, то уравнение изохорического процесса
записывается в виде
P P0 1 αt ,
(4.4.2)
где Р0 – давление при 0 С по Цельсию; α
температурный коэффициент давления газа равен
1/273 град 1.
31. 2. Изобарический процесс. Р = const. Изобарическим процессом называется процесс, протекающий при постоянном давлении Р.
Поведение газа при изобарическомпроцессе подчиняется закону ГейЛюссака:
V/T = const
«При постоянном давлении и
неизменных значениях массы газа и его
молярной массы, отношение объёма
газа к его абсолютной температуре
32. График изобарического процесса на VT диаграмме называется изобарой (рис. 4.8). Полезно знать графики изобарического процесса на
РV и РT диаграммах.Уравнение изобары
V1 V2
T1 T2
33. Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде где температурный
Если температура газа выражена в градусахЦельсия, то уравнение изобарического
процесса записывается в виде
V V0 1 αt ,
1
где α 1 / 273 град температурный
коэффициент объёмного расширения.
34. 3. Изотермический процесс. T = const. Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа приизотермическом процессе подчиняется
закону Бойля-Мариотта:
РV = const
«При постоянной температуре и
неизменных значениях массы газа и его
молярной массы, произведение объёма газа
на его давление остаётся постоянным».
График изотермического процесса на РV
– диаграмме называется изотермой.
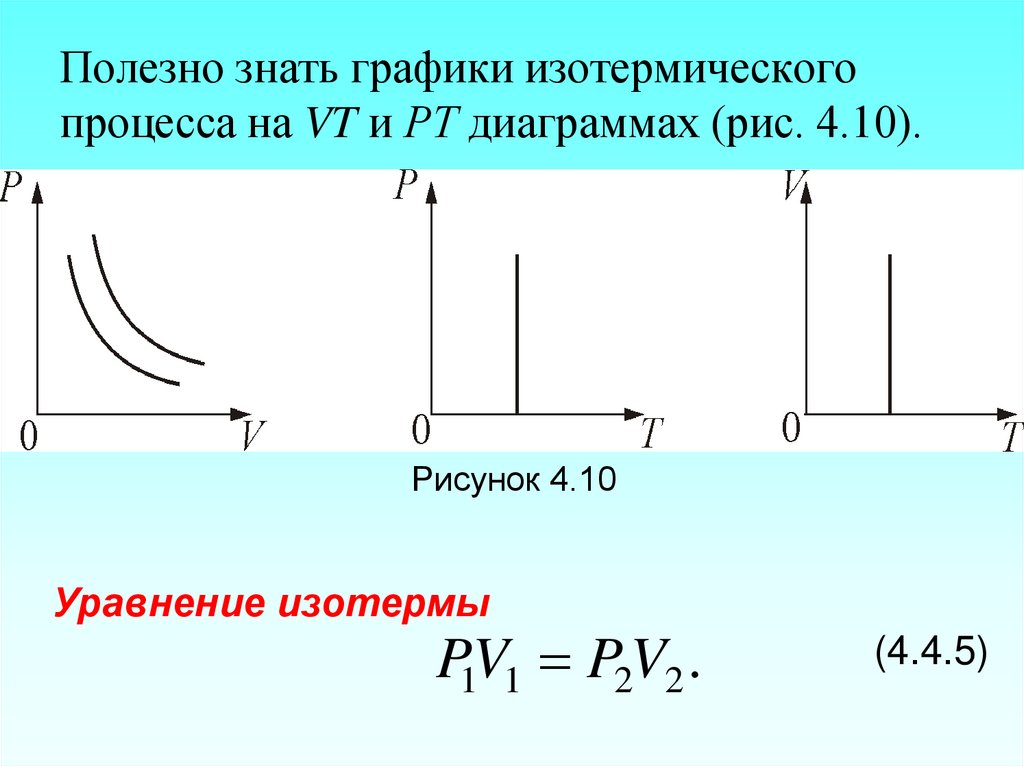
35. Полезно знать графики изотермического процесса на VT и РT диаграммах (рис. 4.10).
Рисунок 4.10Уравнение изотермы
P1V1 P2V2 .
(4.4.5)
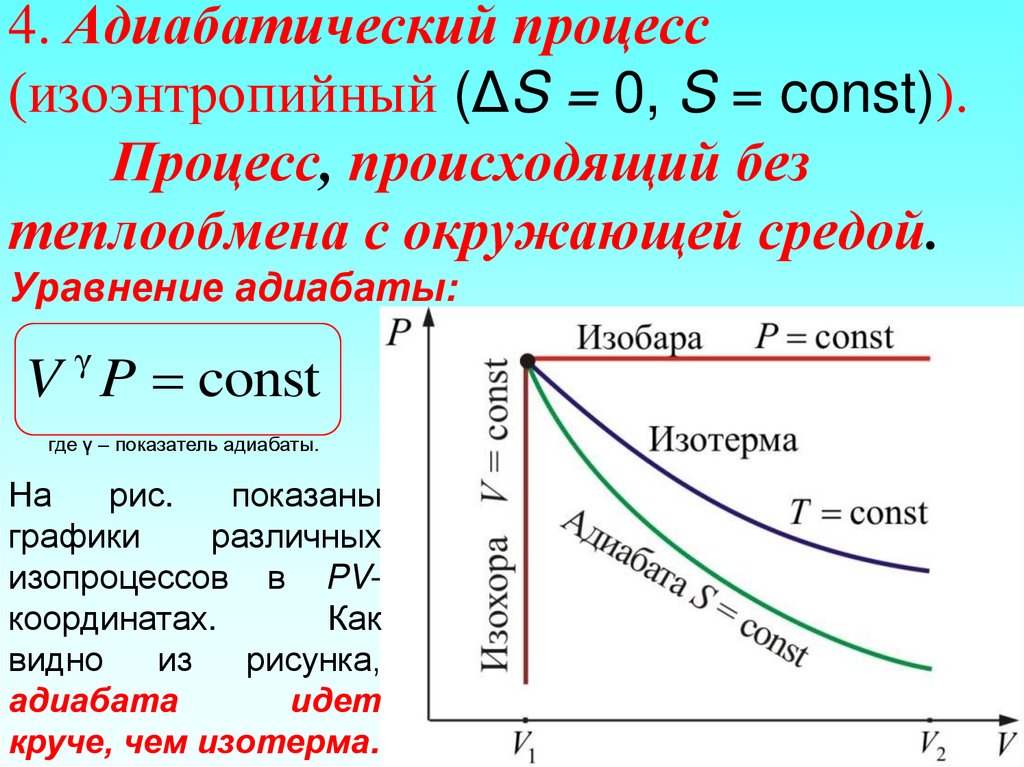
36. 4. Адиабатический процесс (изоэнтропийный (ΔS = 0, S = const)). Процесс, происходящий без теплообмена с окружающей средой.
Уравнение адиабаты:γ
V P const
где γ – показатель адиабаты.
На
рис.
показаны
графики
различных
изопроцессов в PVкоординатах.
Как
видно
из
рисунка,
адиабата
идет
круче, чем изотерма.
37.
5. Политропический процесс.Процесс, при котором теплоёмкость
газа остаётся постоянной.
Политропический процесс – общий
случай всех перечисленных выше
процессов.
38.
6. Закон Авогадро.При одинаковых давлениях и
одинаковых температурах, в равных
объёмах различных идеальных газов
содержится одинаковое число молекул.
В одном моле различных веществ
содержится N A 6,022 10 23
молекул (число Авогадро).
Следствием этого закона является то, что моли
любых газов, при одинаковых температуре и
давлении, занимают одинаковые объемы. При
нормальных условиях объем моля равен:
Vμ = 22,41·10–3 м3/моль.
39. 7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов (Р1 – давление,
7. Закон Дальтона.Давление смеси идеальных газов
равно сумме парциальных давлений Р,
входящих в неё газов
Pсм P1 P2 ... Pn
(Р1 – давление, которое оказывал бы определённый
газ из смеси, если бы он занимал весь объём).
m1RT m2 RT RT m1 m2
Pñì
.
μ1V
μ 2V
V μ1 μ 2
40. 8. Объединённый газовый закон (Закон Клапейрона). В соответствии с законами Бойля - Мариотта (4.4.5) и Гей-Люссака (4.4.3)
можно сделатьзаключение, что для данной массы газа
P1V1 P2V2
или
T1
T2
PV
const.
T
(4.4.7)
Это объединённый газовый закон
Клапейрона.
41. 4.5. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Идеальным газом называют газ, молекулыкоторого пренебрежимо малы, по сравнению
расстояния между ними, и не взаимодействуют
друг с другом на расстоянии.
Все газы, при нормальных условиях, близки
по свойствам к идеальному газу. Ближе всех
газов к идеальному газу – водород.
Уравнение,
связывающее
основные
параметры состояния идеального газа вывел
великий русский ученый Д.И. Менделеев.
42. Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с законом Авогадро. Уравнение, связывающее все эти
законы, называетсяуравнением Менделеева-Клапейрона и
записывается так:
m
PV RT ,
μ
(4.5.1)
m
здесь μ – число молей. Для одного моля
можно записать PVμ RT
43. Если обозначим – плотность газа, то (4.5.2) Если рассматривать смесь газов, заполняющих объём V при температуре Т, тогда,
mρ
Если обозначим V
– плотность газа, то
m
ρ
P
RT RT .
μV
μ
(4.5.2)
Если рассматривать смесь газов,
заполняющих объём V при температуре Т,
тогда, парциальные давления, можно найти,
как:
m1RT
P1
,
μ1V
m2 RT
mn RT
P2
, ….. Pn
μ nV
μ 2V
44. Согласно закону Дальтона: полное давление смеси газа равно сумме парциальных давлений всех газов, входящих в смесь Отсюда, с
Согласно закону Дальтона: полное давлениесмеси газа равно сумме парциальных
давлений всех газов, входящих в смесь
P P1 P2 ... Pn
Отсюда, с учетом вышеизложенного, можно
записать
m1 m2
mn
PV
... RT
(4.5.3)
μn
μ1 μ 2
– это уравнение Менделеева-Клапейрона
для смеси газов.
45. 4.6. Явления переноса в газах
Из прошлых лекций мы знаем, чтомолекулы в газе движутся со скоростью
звука, с такой же скоростью движется пуля.
Однако, находясь в противоположном
конце комнаты, запах разлитой пахучей
жидкости
мы
почувствуем
через
сравнительно
большой
промежуток
времени. Это происходит потому, что
молекулы
движутся
хаотически,
сталкиваются друг с другом, траектория
движения у них ломанная.
46. Рассмотрим некоторые явления, происходящие в газах. Распространение молекул примеси в газе от источника называется диффузией. В
состоянии равновесия температура Т иконцентрация n во всех точках системы
одинакова. При отклонении плотности от
равновесного значения в некоторой части
системы возникает движение компонент
вещества в направлениях, приводящих к
выравниванию концентрации по всему
объему системы.
47. Связанный с этим движением перенос вещества обусловлен диффузией. Диффузионный поток будет пропорционален градиенту
концентрации:dn
J~
dx
48. Если какое либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже
будет испытывать соударения состороны молекул, и получать собственный
импульс, но направленный в противоположную сторону. Газ ускоряется, тело
тормозиться, то есть, на тело действуют
силы трения. Такая же сила трения будет
действовать и между двумя соседними
слоями газа, движущимися с разными
скоростями.
49. Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости: (4.6.1)
Это явление носит название внутреннеетрение или вязкость газа, причём сила
трения
пропорциональна
градиенту
скорости:
dυ
Fтр ~
dx
(4.6.1)
50. Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря
хаотическомудвижению, молекулы в соседних слоях
будут перемешиваться и, их средние
энергии будут выравниваться.
Происходит перенос энергии от более
нагретых слоев к более холодным.
51. называется теплопроводностью. Поток тепла пропорционален градиенту температуры:
Перенос энергии от более нагретыхслоев к более холодным
называется теплопроводностью.
Поток тепла пропорционален
градиенту температуры:
dT
Q~
dx
(4.6.2)
52. В процессе диффузии, при тепло- и электропроводности происходит перенос вещества, а при внутреннем трении – перенос энергии. В
основе этих явлений лежит один и тотже механизм – хаотическое движение
молекул. Общность механизма,
обуславливающего все эти явления переноса,
приводит к тому, что их закономерности
должны быть похожи друг на друга.
53. 4.7. Число столкновений и средняя длина свободного пробега молекул в газах
Обозначимλ i– длина свободного
пробега молекулы.
Медленность
явлений
переноса,
например
диффузии
ароматических
веществ – «распространение запаха»,
при
относительно
высокой
скорости
теплового движения молекул объясняется
столкновениями молекул.
2
3
10 10 м/с
54. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега: – средняя скорость
Расстояние, проходимое молекулой всреднем без столкновений, называется
средней длиной свободного пробега:
λ υср τ,
υ ср – средняя скорость теплового
движения, τ – среднее время между двумя
столкновениями.
Именно λ средняя длина
свободного пробега, нас и интересует
(рисунок 4.1).
55.
λiРисунок 4.1
56. Модель идеального газа – твёрдые шарики одного диаметра, взаимодействую-щие между собой только при столкновении. Обозначим σ –
Модель идеального газа – твёрдыешарики одного диаметра, взаимодействующие между собой только при столкновении.
Обозначим σ – эффективное сечение
молекулы – полное поперечное сечение
рассеяния, характеризующее столкновение
между двумя молекулами (рисунок 4.2).
57.
σ– эффективное
сечение молекулы
Рисунок 4.2
σ πd
2
– площадь в которую не может
проникнуть центр любой другой молекулы.
58. За одну секунду молекула проходит путь, равный средней арифметической скорости За ту же секунду молекула претерпе-вает ν
За одну секунду молекула проходитпуть, равный средней арифметической
скорости υ
За ту же секунду молекула претерпевает ν столкновений.
υ
λ
ν
59. Подсчитаем число столкновений ν. Вероятность столкновения трех и более молекул бесконечно мала. Предположим, что все молекулы
застыли, кроме одной. Её траекториябудет представлять собой ломаную
линию. Столкновения будут только с
теми молекулами, центры которых лежат
внутри цилиндра радиусом d (рисунок
4.3).
60.
Путь, который пройдетмолекула за одну секунду, равен
длине цилиндра υ'
υ' σ - объём цилиндра
n - число молекул в единице объёма
среднее число столкновений в одну секунду:
ν πd υ' n.
2
Рисунок 4.3
υ'
61. На самом деле, все молекулы движутся (и в сторону и навстречу друг другу), поэтому число соударений определяется средней
скоростью движения молекулотносительно друг друга υ
По закону сложения случайных величин:
υ' υ υ 2 υ υ 2.
2
2
2
υ
Так как λ
- средняя длина свободного пробега
ν
Тогда:
1
1
λ
.
2
2nπd
2nσ
62. Из уравнения состояния идеального газа выразим n через давление P и температуру Т Так как , то есть тогда
Из уравнения состояния идеального газавыразим n через давление P и температуру Т
P
Так как P nkT , то есть n
, тогда
kT
λ
kT
kT
.
2
2πd P
2σP
63. Таким образом, при заданной температуре, средняя длина свободного пробега обратно пропорциональна давлению Р: Например: d = 3 Å
Таким образом, при заданной температуре,средняя длина свободного пробега обратно
пропорциональна давлению Р:
1
~
P
Например: d = 3 Å = 3 10 10 м,
7
Р = 1 атм., Т = 300 К,
λ 10 м
3
а, т.к υ 10 м/с
3
10
10 столкновений.
ν 7 10
10
64. 4.8. Диффузия газов
Диффузия от латинского diffusio –распространение, растекание взаимное
проникновение соприкасающихся веществ
друг в друга, вследствие теплового
движения частиц вещества.
Диффузия происходит в направлении
уменьшения концентрации вещества и ведет
к его равномерному распределению по
занимаемому объему.
65. Диффузия имеет место в газах, жидкостях и твердых телах. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях,
ещемедленнее в твердых телах, что обусловлено
характером движения частиц в этих средах.
Для газа диффузия – это распределение
молекул примеси от источника
(или взаимная диффузия газа).
66. Обозначим: – коэффициент диффузии. Тогда диффузионный поток будет равен: (4.7.2) или в общем случае (в трёхмерной системе)
1Обозначим: D λ υ – коэффициент
3
диффузии.
Тогда диффузионный поток будет равен:
dn
J D ,
dx
(4.7.2)
или в общем случае (в трёхмерной системе)
J D grad n
– уравнение Фика.
(4.7.3)
67. Из уравнения Фика видно, что диффузионный поток, направлен в сторону уменьшения концентрации. При этом коэффициент диффузии D
J D grad nИз уравнения Фика видно, что
диффузионный поток, направлен в сторону
уменьшения концентрации.
При этом коэффициент диффузии D
численно равен диффузионному потоку
через единицу площади в единицу времени
при grad n 1
Измеряется коэффициент диффузии D
в м/с2.
68. 4.9. Внутреннее трение. Вязкость газов
Рассмотрим ещё одну систему координат: υот х
(рисунок 4.5)
69. Пусть в покоящемся газе вверх, перпендикулярно оси х движется пластинка со скоростью υ0, причём (υT – скорость теплового
Пусть в покоящемся газе вверх,перпендикулярно оси х движется пластинка
υ0
со
скоростью
υ0, υT
причём
(υT – скорость теплового движения молекул).
Пластинка
увлекает
за
собой
прилегающий слой газа, тот слой – соседний
и так далее. Весь газ делится, как бы на
тончайшие слои, скользящие вверх тем
медленнее, чем дальше они от пластинки.
Раз слои газа движутся с разными
скоростями, возникает трение.
Выясним причину трения в газе.
70. Каждая молекула газа в слое принимает участие в двух движениях: тепловом и направленном. Так как направление теплового движения
хаотически меняется, то всреднем вектор тепловой скорости равен
нулю
υT 0
.
При направленном движении вся
совокупность молекул будет дрейфовать
с постоянной скоростью υ.
71. Средний импульс отдельной молекулы в слое определяется только дрейфовой скоростью υ: Но так как молекулы участвуют в тепловом
Средний импульс отдельной молекулы в слоеопределяется только дрейфовой скоростью υ:
p0 m0 υ.
Но так как молекулы участвуют в тепловом
движении, они будут переходить из слоя в слой.
При этом они будут переносить с собой
добавочный импульс, который будет
определяться молекулами того слоя, куда
перешла молекула.
Перемешивание молекул разных слоёв
приводит к выравниванию дрейфовых
скоростей разных слоёв, что и проявляется
макроскопически как действие сил трения
между слоями.
72. Сила, действующая на единицу площади поверхности, разделяющей два соседних слоя газа: Или, в общем виде Это уравнение Ньютона.
Сила, действующая на единицу площадиповерхности, разделяющей два соседних
dυ
слоя газа:
f η
dx
.
f η grad υ.
Или, в общем виде
Это уравнение Ньютона.
Здесь η – коэффициент вязкости:
1
η λ υ nm0 Dρ, (4.7.3)
3
где D – коэффициент диффузии; ρ – плотность газа
73. Физический смысл коэффициента вязкости η в том, что он численно равен импульсу, переносимому в единицу времени через единицу
1η λ υ nm0 Dρ,
3
Физический смысл коэффициента
вязкости η в том, что он численно равен
импульсу, переносимому в единицу времени
через единицу площади при градиенте
скорости равном единице.
74. 4.10. Теплопроводность газов
Учение о теплопроводностиначало развиваться в XVIII в. и
получило свое завершение в
работах французского ученого Ж.
Фурье (1786 – 1830),
опубликовавшего в 1822 г. книгу
«Аналитическая теория теплоты».
75. или (4.10.1) – уравнение теплопроводности Ж.Фурье. Здесь q – тепловой поток; χ – коэффициент теплопроводности, равный: или
илиq χ grad T
(4.10.1)
– уравнение теплопроводности Ж.Фурье.
Здесь q – тепловой поток;
χ – коэффициент теплопроводности,
равный:
1
i
χ λ υT n k
3
2
1
χ λ υT ρCVУД
3
или
(4.10.2)
(4.10.3)
76. υТ – тепловая скорость молекул; – удельная теплоемкость при постоянном объеме. Найдем размерность коэффициента
1χ λ υT ρCVУД
3
υТ – тепловая скорость молекул;
CVуд– удельная теплоемкость при
постоянном объеме.
Найдем размерность коэффициента
теплопроводности:
qdx
Дж м
кг м
χ
2
3
dT м К с с К
77. 4.11. Уравнения и коэффициенты переноса
Сопоставим уравнения переносаJ Dgrad n
dn
J D
dx
Уравнение Фика для диффузии.
Коэффициент диффузии
1
D λ υT
3
78.
f тр η grad υdυ
или f
Уравнение Ньютона
η
тр
dx
для трения.
Коэффициент вязкости:
1
η λ υT nm0 Dρ.
3
79. 4.12. Внутренняя энергия. Работа и теплота
Наряду с механической энергией любое тело(или система) обладает внутренней энергией.
Внутренняя энергия – энергия покоя.
Она складывается из:
1. теплового хаотического
движения молекул,
2. потенциальной энергии их
взаимного
расположения,
3. кинетической и потенциальной энергии
электронов в атомах, нуклонов в ядрах и т. д.
80. В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы
В термодинамике важно знать неабсолютное значение внутренней энергии,
а её изменение.
В
термодинамических
процессах
изменяется только кинетическая энергия
движущихся молекул (тепловой энергии
недостаточно, чтобы изменить строение
атома,
а
тем
более
ядра).
Следовательно, фактически под
внутренней энергией в термодинамике
подразумевают энергию теплового
хаотического движения молекул.
81. Внутренняя энергия U одного моля идеального газа равна: или Таким образом, внутренняя энергия зависит только от температуры.
Внутренняя энергия U одного моляидеального газа равна:
3
3
U N A K kTN A RT , или
2
2
3
U RT
2
Таким образом, внутренняя энергия зависит
только от температуры.
Внутренняя энергия U является функцией
состояния системы независимо от предыстории
82.
Для идеального газа внутренняя энергиясистемы равна сумме кинетических энергий
ее частиц:
mi
i
i
RT RT
U n K nkT U
2
2
2
Функции состояния – величины, изменение
которых при переходе системы между
состояниями не зависит от способов этих
переходов, т.е. от вида переходных процессов.
83. Понятно, что в общем случае термодинамическая система может обладать как внутренней, так и механической энергией и разные
системы могут обмениваться этимивидами энергии.
Обмен механической энергией
характеризуется совершенной работой
А,
а обмен внутренней энергией –
количеством переданного тепла Q.
84. Итак, работа и теплота не есть особые формы энергии. Нельзя говорить о запасе теплоты или работы. Это мера переданной другой
системемеханической или внутренней энергии. О запасе
этих энергий можно говорить.
Механическая энергия может
переходить в тепловую энергию и обратно.
Например, если стучать молотком по
наковальне, то через некоторое время
молоток и наковальня нагреются (пример
диссипации энергии)
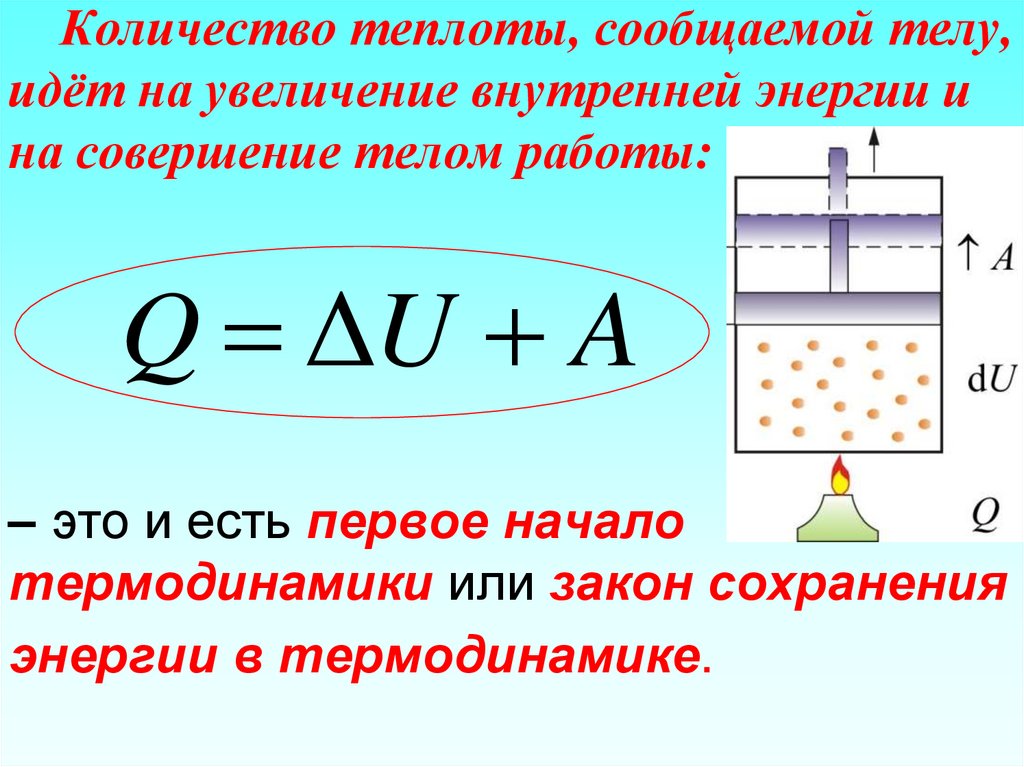
85. Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: – это и есть первое
Количество теплоты, сообщаемой телу,идёт на увеличение внутренней энергии и
на совершение телом работы:
Q ΔU A
– это и есть первое начало
термодинамики или закон сохранения
энергии в термодинамике.
86.
87. Правило знаков: если тепло передаётся от окружающей среды данной системе, при этом Если система производит работу над
Правило знаков: ΔQ 0, если тепло передаётсяот окружающей среды данной системе, при этом
ΔU 0
ΔA 0,
Если система производит работу над
окружающими телами, то: U 0
Учитывая правило знаков, первое начало
термодинамики можно записать в виде:
ΔU Q A
– изменение внутренней энергии тела
равно разности сообщаемой телу
теплоты и произведённой телом работы.
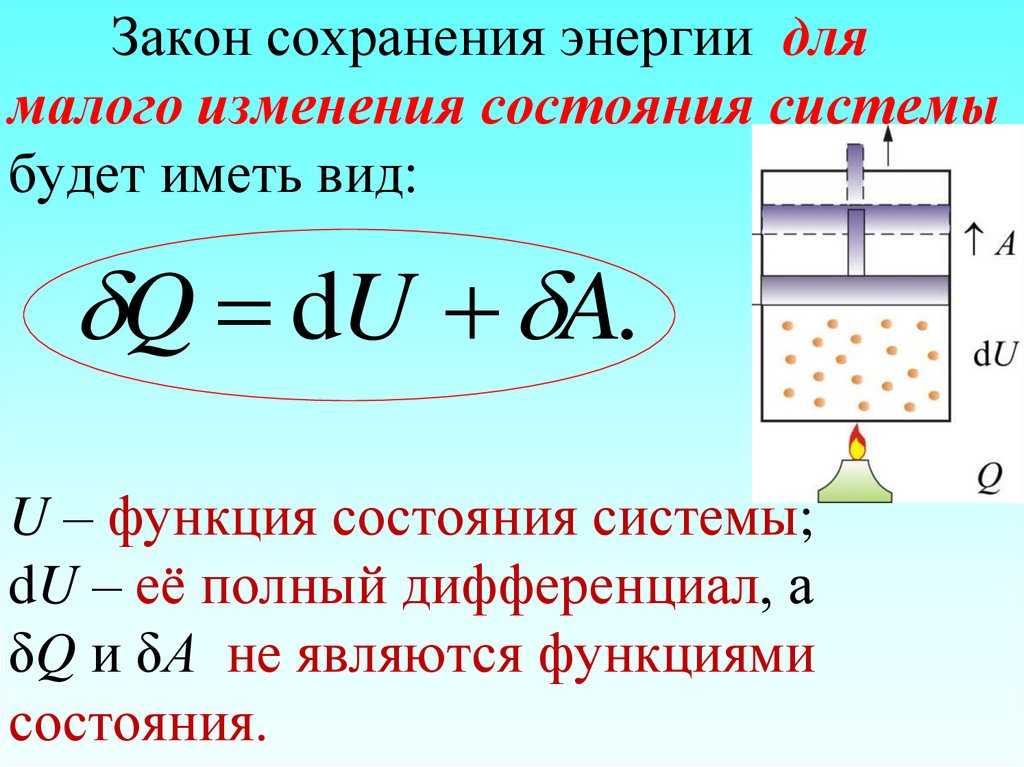
88. Закон сохранения энергии для малого изменения состояния системы будет иметь вид: U – функция состояния системы; dU – её полный
Закон сохранения энергии длямалого изменения состояния системы
будет иметь вид:
Q dU A.
U – функция состояния системы;
dU – её полный дифференциал, а
δQ и δА не являются функциями
состояния.
89.
В каждом состоянии система обладаетопределенным и только таким значением
внутренней энергии, поэтому можно записать
U2
U dU U 2 U 1
U1
Так как U – функция состояния, то
d
U
0
.
Это справедливо для любой функции состояния.
90. Теплота Q и работа А зависят от того, каким образом совершен переход из состояния 1 в состояние 2 (изохорически,
адиабатически), а внутренняя энергия U независит.
При этом нельзя сказать, что система,
обладает определенным для данного
состояния значением теплоты и работы.
Количество теплоты Q выражается в тех
же единицах, что работа и энергия, т.е. в
джоулях [Q] = Дж.
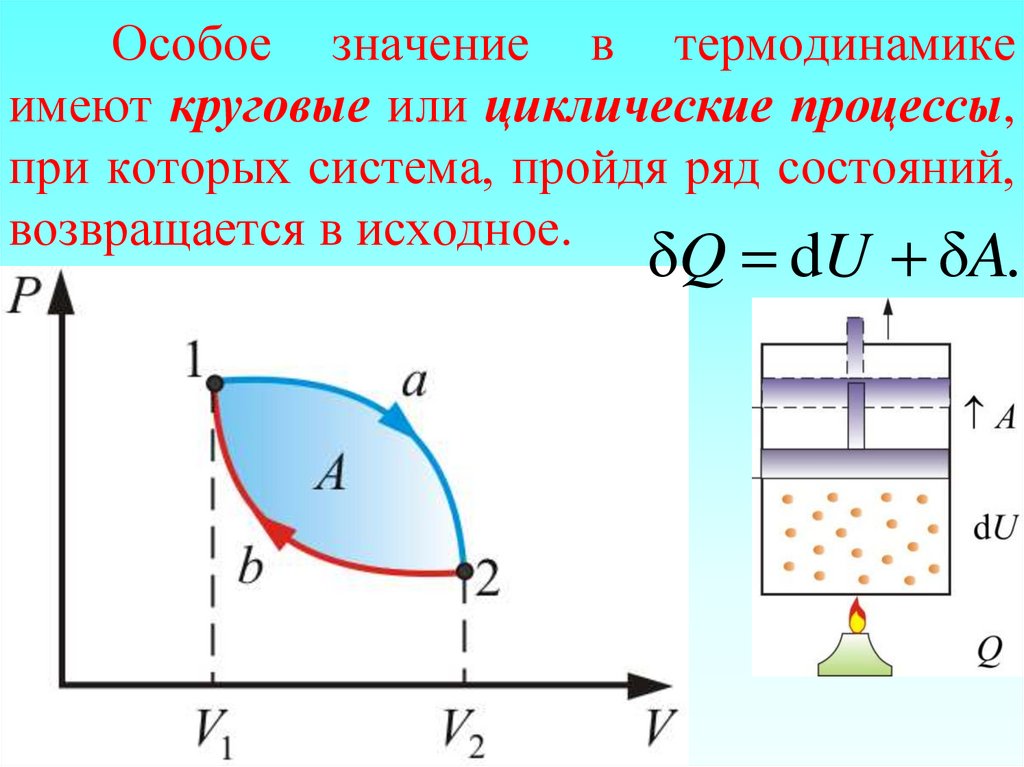
91. Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний,
возвращается в исходное.δQ dU δA.
92. Если то согласно первому началу термодинамики т.е. нельзя построить периодически действующий двигатель, который совершал бы
Если ΔU 0, то согласно первомуA Q,
началу термодинамики
т.е.
нельзя построить периодически
действующий
двигатель,
который
совершал бы бóльшую работу, чем
количество сообщенной ему извне энергии.
Иными словами, вечный
двигатель
первого
невозможен.
рода
Это одна из формулировок первого
начала термодинамики.
93. первое начало термодинамики не указывает, в каком направлении идут процессы изменения состояния.
Недостатки первого начала :первое начало термодинамики
не указывает, в каком направлении
идут
процессы
изменения
состояния.
94. 1. Теплоёмкости одноатомных газов
Теплоёмкости одноатомных имногоатомных газов
1. Теплоёмкости одноатомных газов
Т.к. внутренняя энергия одного моля
dU
3
идеального газа равна U RT , а CV
,
dT
2
то
3
кДж
CV R 12,5
,
2
кмоль К
теплоемкость при постоянном объеме СV –
величина постоянная, от температуры не зависит.
95.
dQ dU dA Учитывая физический смысл Rдля изобарических процессов можно
записать: dQ dU RdT
P
μ
dQP dU
dT
CP
R
dT
dT
dT
3
CP R R
2
Теплоемкость при постоянном
давлении для одноатомных газов:
5
кДж
CP R 20,8
.
2
кмоль К
96. - постоянная адиабаты (коэффициент Пуассона)
СРγ,
СV
- постоянная адиабаты
(коэффициент Пуассона)
20,8
γ
1,67.
12,5
97. Так как Тогда Из этого следует, что (4.3.5) Кроме того , где i – число степеней свободы молекул.
Так какСP CV R
R
γ
1
.
СV
CV
CV
R
γ
1
Тогда
CV
Из этого следует, что
R
CV
.
γ 1
i 2
γ
Кроме того
i ,
(4.3.5)
где i – число степеней свободы молекул.
98. Подставив в выражение для внутренней энергии, получим: а так как , то внутреннюю энергию можно найти по формуле: (4.3.6)
Подставив СV в выражение для внутреннейэнергии, получим: U m C T m R T ,
μ
а так как
PV
m
RT
V
μ γ 1
, то
внутреннюю энергию можно найти по
формуле:
PV
U
.
γ 1
(4.3.6)
99. Теплоемкости многоатомных газов
Опыты с двухатомными газами такими каказот, кислород и др. показали, что
кДж
CV 20,8
.
кмоль К
Для водяного пара и других многоатомных газов
(СН3, СН4, и так далее)
кДж
СV 25
кмоль К
.
То есть молекулы многоатомных газов нельзя
рассматривать как материальные точки
Необходимо учитывать вращательное движение
молекул и число степеней свободы этих молекул. .
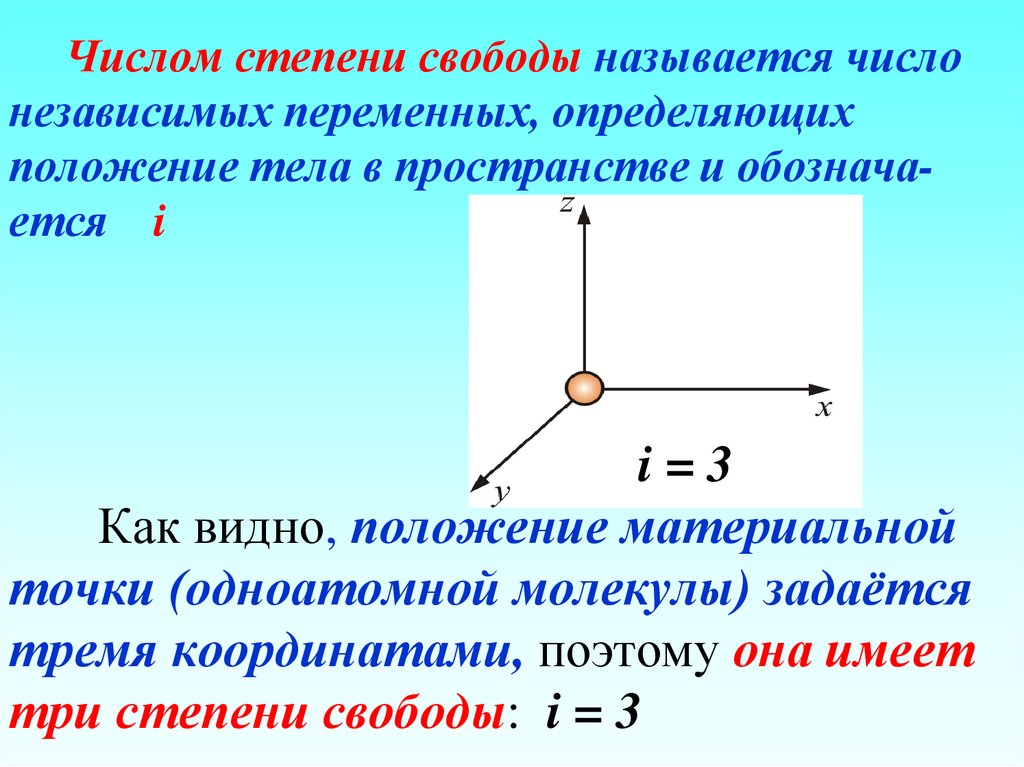
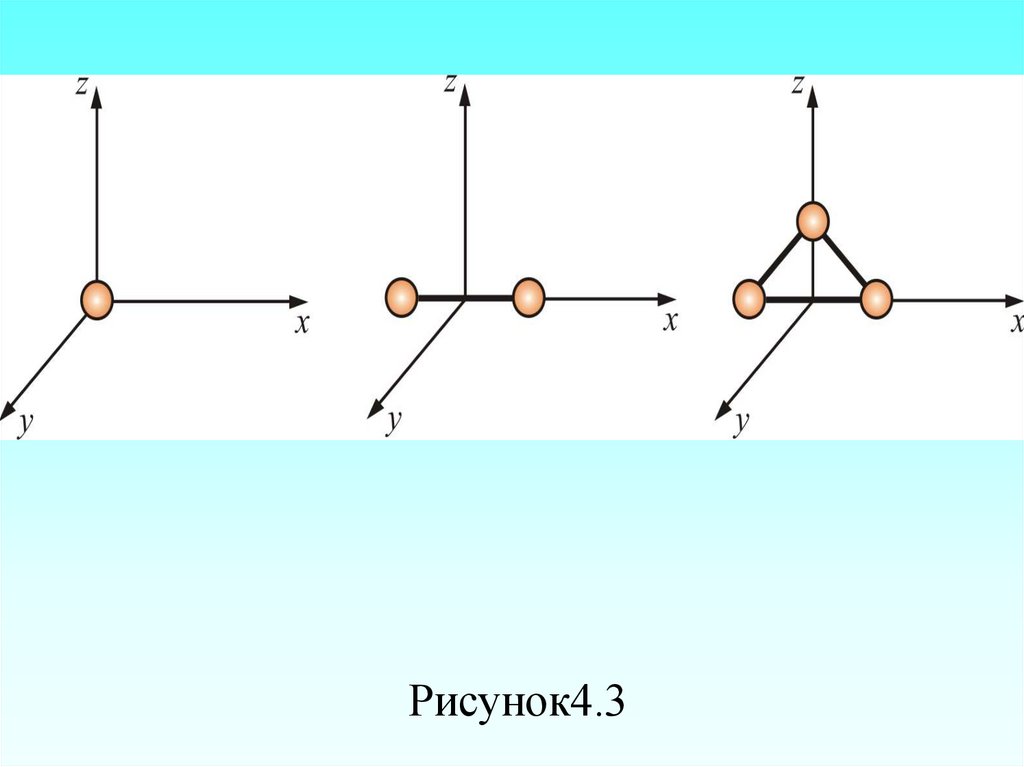
100. Числом степени свободы называется число независимых переменных, определяющих положение тела в пространстве и обознача-ется i i
Числом степени свободы называется числонезависимых переменных, определяющих
положение тела в пространстве и обозначается i
i=3
Как видно, положение материальной
точки (одноатомной молекулы) задаётся
тремя координатами, поэтому она имеет
три степени свободы: i = 3
101. Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два
независимых вращения, алюбое вращение можно разложить на три
вращательных движения вокруг взаимно
перпендикулярных
осей.
Но
для
двухатомных молекул вращение вокруг оси z
не изменит её положение в пространстве, а
момент инерции относительно этой оси
равен нулю (рисунок 9.3).
102.
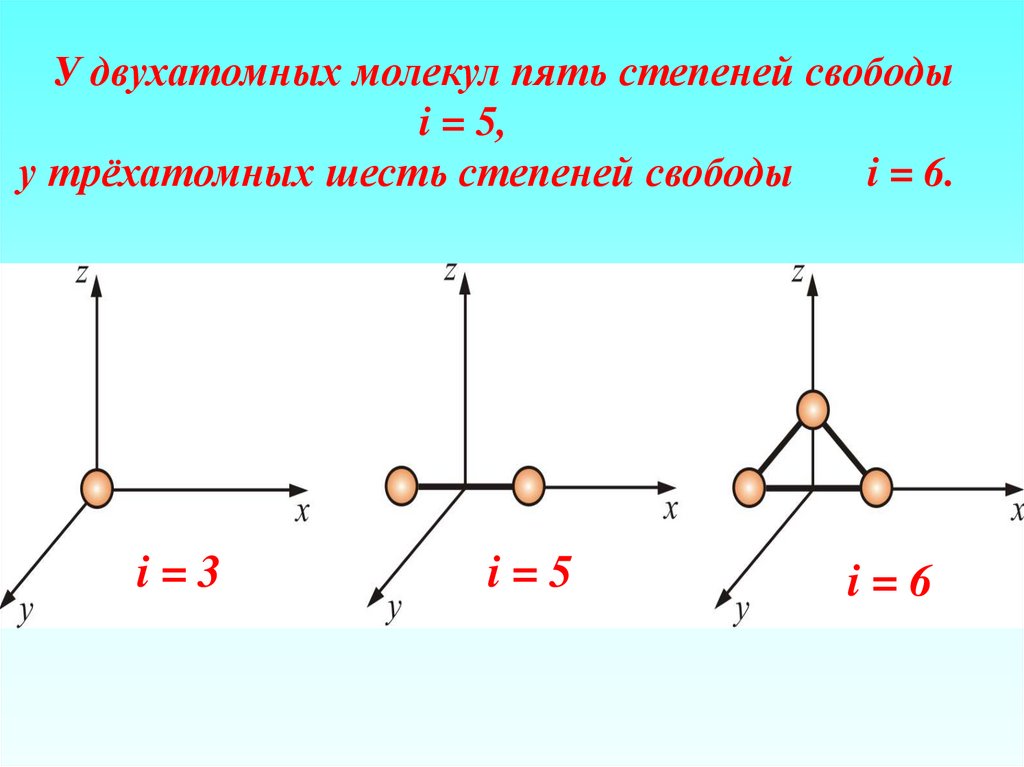
Рисунок4.3103.
У двухатомных молекул пять степеней свободыi = 5,
у трёхатомных шесть степеней свободы
i = 6.
i=3
i=5
i=6
104. Больцман доказал, что, средняя энергия приходящаяся на одну степень свободы равна
Закон о равномерном распределенииэнергии по
степеням свободы
Больцман доказал, что, средняя
энергия
K
приходящаяся на одну степень
свободы равна
1
kT .
2
105.
Итак, средняя энергия приходящаяся наодну степень свободы:
1
K kT .
2
(4.4.1)
106. У одноатомной молекулы i = 3, тогда для двухатомных молекул i = 5 для трёхатомных молекул i = 6
У одноатомной молекулы i = 3, тогда3
K kT ,
2
для двухатомных молекул i = 5
5
K kT ,
2
для трёхатомных молекул i = 6
6
K kT .
2
107. На среднюю кинетическую энергию молекулы, имеющей i-степеней свободы приходится (4.4.5) Это и есть закон Больцмана о
На среднюю кинетическую энергиюмолекулы, имеющей i-степеней свободы
приходится
i
K kT
2
(4.4.5)
Это и есть закон Больцмана о
равномерном распределении средней
кинетической энергии по степеням
свободы.
Здесь
i = iп + iвр + 2iкол
(4.4.6)
108.
i iпост iв ращ 2iколеб109. Для произвольного количества газов: , (4.4.9) (4.4.10) Из теории также следует, что СV не зависит от температуры (рис.).
Для произвольного количества газов:mi
CV
R
μ2
,
mi 2
CP
R.
μ 2
Из теории также следует, что СV не
зависит от температуры (рис.).
(4.4.9)
(4.4.10)
110. 4.13. Применение первого начала термодинамики к изопроцессам идеальных газов
В таблице приводятся сводные данные охарактеристиках изопроцессов в газах.
Изопроцессы
–
процессы,
при
которых
один
из
термодинамических параметров остается постоянным
Здесь используются известные нам формулы:
δQ dU δA – I начало термодинамики
или
закон
сохранения
энергии
в
термодинамике:
111.
Сводные данные о характеристиках изопроцессов в газах.Процесс
Условие
протекания
Первое
начало
Изотермическое
расширение
р 1
Q A
Q 0
2
T const0
Изотермическое p
сжатие
А
0
A 0
0
A 0
V
Q A
1
Q
0
V
2
T const 0
Изохорное
нагревание
U
p
Q U
Q 0
2
V const
1
0
V
U Q
U 0
0
112.
ПроцессИзохорное
охлаждение
Первое
начало
p
Q U U Q
Q 0 U 0
р
1
2 Q U A U Q A
Q 0
p const
0
p
2
U 0
V
1 Q U A U Q A
Q 0
p const
0
А
0
V
0
Изобарное
расширение
Изобарное
сжатие
1
2
V const
U
Условие
протекания
V
U 0
p V2 V1
m
R T2 T1
A 0
p V2 V1
m
R T2 T1
A 0
113.
Адиабатный процесс - процесс, при которомотсутствует теплообмен с окружающей
средой. Q 0
A U
1 начало термодинамики
В случае адиабатного процесса система совершает работу
за счет убыли внутренней энергии
PV const
Уравнение Пуассона:
Cp
γ
CV
γ
показатель адиабаты
Адиабатные процессы применяются в двигателях внутреннего сгорания
(расширение и сжатие горючей смеси в цилиндрах), в холодильных установках.
114. Работа газа в адиабатном процессе
mdQ 0 dU CV dT
μ
m
A CV dT
μ
A P dV
mi
А
R dT
μ 2
p 1
T const
2
Q 0
0
V1
V2
V
V1
m P1V1
1
А
μ γ 1
V2
γ 1
Работа
при
адиабатном
расширении, меньше, чем при
изотермическом: при адиабатном
процессе происходит охлаждение
газа, тогда как при изотермическом
Т = const за счет притока извне
эквивалентного количества теплоты.
115. Сравнение адиабатного и изотермического процессов
γPV
const уравнение
Q 0
адиабаты
p
T const
0
p
V1
V2
T const
Q 0
0 V
1
V2
> 1, поэтому адиабата
V идет круче, чем изотерма.
Причина:
При адиабатном сжатии
(расширении) газ нагревается
(охлаждается) поэтому
увеличение (уменьшение) Р
обусловлено не только
изменением V (как при
V изотермическом процессе),
но и изменением Т.
116. Основная таблица ТД Применение первого начала термодинамики к изопроцессам идеальных газов
117.
Название процессаИзохорический
Условие
протекания
процесса
V = const
Изобарический
Изотермический
P = const
T = const
Закон
Закон Шарля
Гей-Люссака
Связь между
параметрами
состояния
P
const
T
Первое
начало ТД
δQ d U
V
const
T
PdV
m
RdT
μ
Работа в
процессе
A 0
m
A RΔT
μ
V2
A PdV
V1
A P(V2 V1 )
γ
CP i 2
CV
i
PV γ const
PV const
TV γ 1 const
T γ P γ 1 const
δQ dU δA δQ δA
δA PdV
δA 0
Закон Бойля –
Мариотта
Адиабатический
δQ = 0
dU δA
δA = PdV = dU
δA PdV
A
A
А = −∆U = – CVΔТ
m
V
RT ln 2 δA m i RdT
μ
V1
μ 2
m
Р
RT ln 1
μ
Р2
γ 1
P1V1 V1
1
A
γ 1 V2
118.
Количествотеплоты,
сообщённое в
процессе
δQ d U
δQ CV dT
Q CV ΔТ
dU = δQ
Изменение
внутренней
энергии
i
ΔU VΔP
2
Теплоёмкость
Q = СP (T2 T1)
Q
m i
1 R ΔT
μ 2
dU = СV dT
U = СV (T2 T1)
i
ΔU PΔV
2
V
ΔР
γ 1
mi
ΔU
RΔT
μ 2
dU i
R
dT 2
CP
ΔU
CV
δQ = СP dT
δQ = δA
Q=A
δQ = 0
Q=0
dU = δA
dU = 0
U = –A = –СV ΔT
P1V1
ΔU
T1 ( γ 1)
m γR
μ ( γ 1)
m R
CV
μ ( γ 1) C dQ i 1 R
P
dT 2
CТ =
Сад = 0
119. Здесь уместно рассмотреть еще и политропный процесс – такой процесс, при котором изменяются все основные параметры системы,
кроме теплоемкости,т.е.
С = const.
Уравнение политропы
PV const
n
(4.5.1)
или
TV
n 1
const .
Здесь n – показатель политропы.
(4.5.2)
120. С помощью показателя n можно легко описать любой изопроцесс: 1. Изобарный процесс Р = const, n = 0 (4.5.3) 2. Изотермический
С помощью показателя n можно легкоописать любой изопроцесс:
1. Изобарный процесс Р = const, n = 0
γR
C
γCV CP .
γ 1
(4.5.3)
2. Изотермический процесс Т = const, n = 1,
CT .
3. Изохорный процесс V = const,
R
CV
.
γ 1
n
(4.5.4)
121. 4. Адиабатический процесс Q = 0, n = γ, Сад = 0. Во всех этих процессах работу можно вычислить по одной формуле: (4.5.5)
4. Адиабатический процесс Q = 0, n = γ,Сад = 0.
Во всех этих процессах работу можно
вычислить по одной формуле:
V1
P1V1
1
A
n 1 V2
n 1
(4.5.5)












































































































 physics
physics








