Elements of Econometrics. Lecture 24. Revision Time Series 1

1.

Elements of Econometrics.
Lecture 24.
Revision Time Series 1.
ICEF, 2022-2023

2.

Basic Regression Analysis with Time Series Data
• The nature of time series data
• Temporal ordering of observations; may not be arbitrarily reordered
• Typical features: serial correlation/nonindependence of observations
• How should we think about the randomness in time series data?
– The outcome of economic variables (e.g. GDP, Inflation Rates) is uncertain; they
should therefore be modeled as random variables.
– Time series are sequences of random variables (= stochastic processes)
– Randomness does not come from sampling from a population.
– “Sample” = the one realized path of the time series out of the many possible paths
the stochastic process could have taken.

3.

Time Series Data Specifics Essential for Regression Models
• Assumption B.2 is irrelevant (the observations do not look as being taken
randomly from fixed populations): B.2 to be replaced by another assumption
There may be regularities in the time series and in their relationships: trends,
seasonalities, autocorrelations in variables and disturbance terms, lags (fixed
or distributed); to be identified and dealt with
• Some regularities in the data (nonstationarity) may lead to estimation of
spurious regressions: the data/model has to be transformed to provide
desirable estimators’ properties

4.

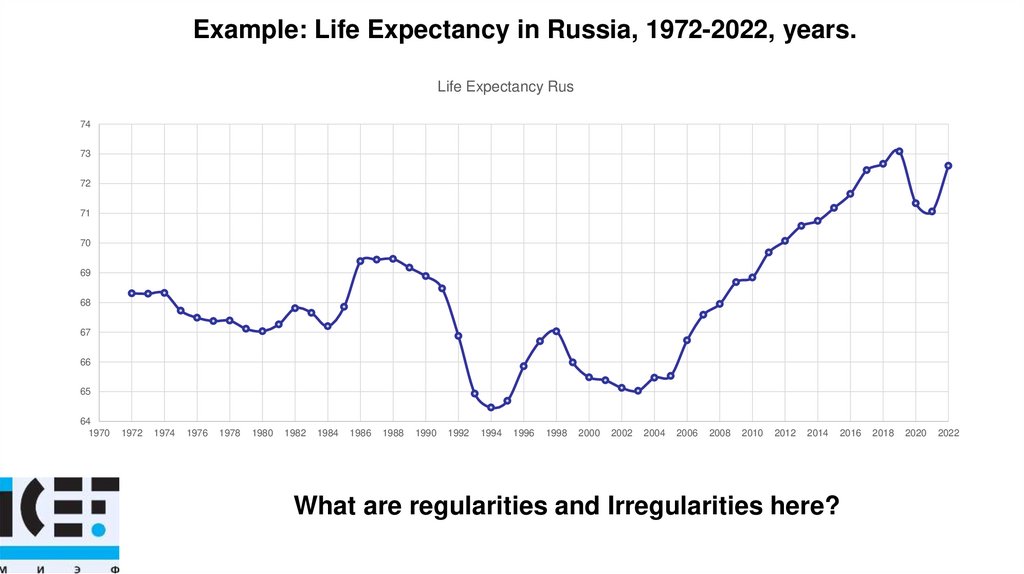
Example: Life Expectancy in Russia, 1972-2022, years.
Life Expectancy Rus
74
73
72
71
70
69
68
67
66
65
64
1970
1972
1974
1976
1978
1980
1982
1984
1986
1988
1990
1992
1994
1996
1998
2000
2002
2004
2006
2008
2010
2012
2014
2016
What are regularities and Irregularities here?
2018
2020
2022

5.

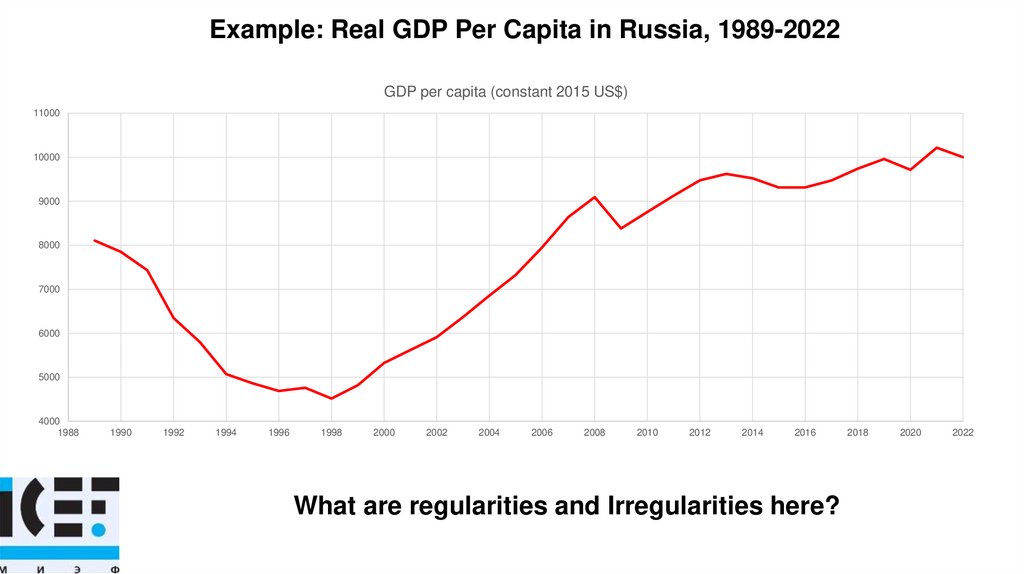
Example: Real GDP Per Capita in Russia, 1989-2022
GDP per capita (constant 2015 US$)
11000
10000
9000
8000
7000
6000
5000
4000
1988
1990
1992
1994
1996
1998
2000
2002
2004
2006
2008
2010
2012
2014
2016
What are regularities and Irregularities here?
2018
2020
2022

6.

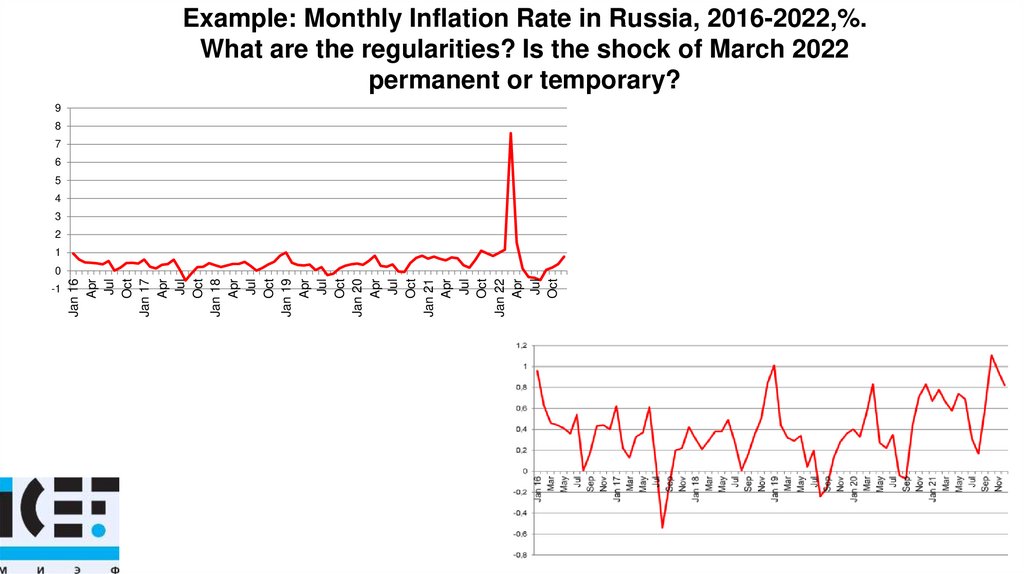
Example: Monthly Inflation Rate in Russia, 2016-2022,%.
What are the regularities? Is the shock of March 2022
permanent or temporary?
9
8
7
6
5
4
3
2
1
-1
Jan 16
Apr
Jul
Oct
Jan 17
Apr
Jul
Oct
Jan 18
Apr
Jul
Oct
Jan 19
Apr
Jul
Oct
Jan 20
Apr
Jul
Oct
Jan 21
Apr
Jul
Oct
Jan 22
Apr
Jul
Oct
0

7.

ASSUMPTIONS FOR MODEL C: REGRESSIONS WITH TIME SERIES DATA
ASSUMPTIONS FOR MODEL C
C.1
The model is linear in parameters and correctly specified
Y = b1 + b2X2 + … + bkXk + u
C.2
The time series for the regressors are (at most) weakly persistent
C.3
There does not exist an exact linear relationship among the regressors
C.4
The disturbance term has zero expectation
C.5
The disturbance term is homoscedastic
C.6
The values of the disturbance term have independent distributions:
ut is distributed independently of ut' for t' ≠ t
The disturbance term is distributed independently of the regressors:
ut is distributed independently of Xjt' for all t' (including t) and j
The disturbance term has a normal distribution
C.7
C.8
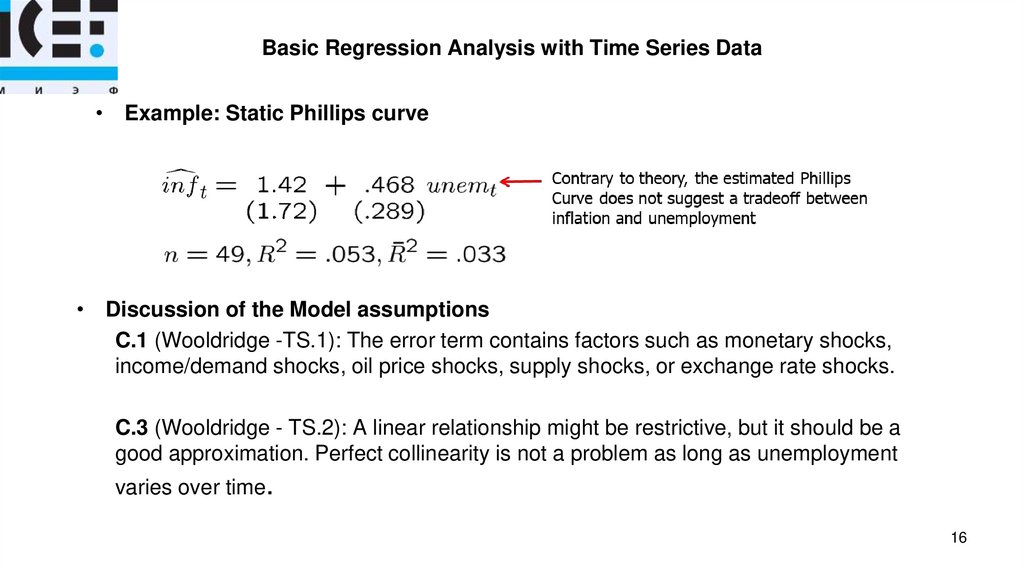
Assumptions C.1, C.3, C.4, C.5, C.6, C.7 and C.8, and the consequences of their violations are
the same as those for Model B. Weak persistency (or weak non-stationarity), C.2: see the
slide below.

8.

Stationary Stochastic Processes
Stationarity (strong stationarity) of a stochastic process Xt is
observed if the joint distribution of Xt1,Xt2,…,Xtm is identical to
the joint distribution of Xt1+t,Xt2+t,…,Xtm+t for any m,t,t1,…,tm.
A stochastic process is weakly stationary (or covariance
stationary) if E(Xt) is constant, Var(Xt) is constant, and for any
t,s ≥ 1, Cov(Xt, Xt+s) depends only on s and not on t
If for a weakly stationary process Cov(Xt,Xt+s) → 0 as s → ∞,
the process is called weakly dependent (or weakly persistent)

9.

ASSUMPTION C.7
ASSUMPTIONS FOR MODEL C
C.7 The disturbance term is distributed independently of the regressors
ut is distributed independently of Xjt' for all t' (including t) and j
(1) The disturbance term in any observation is distributed
independently of the values of the regressors in the same
observation, and
(2) The disturbance term in any observation is distributed
independently of the values of the
regressors in the other observations.
Assumption C.7, like its counterpart Assumption B.7, is essential for both the unbiasedness
and the consistency of OLS estimators. Both parts are required for unbiasedness. However
only the first part is required for consistency (as a necessary, but not sufficient, condition).

10.

UNBIASEDNESS
σ