Виды потенциалов притяжения. Лекция 12

1.

Виды потенциалов
притяжения
Лекция 12
Лектор Исаева Л.Д.

2.

План лекции
• Магнитная масса
• Потенциал диполя
• Потенциал притяжения двойного слоя.

3.

Магнитная масса.
• В качестве магнитных масс рассматриваются
намагниченные тела.
Взаимодействие между двумя
изолированными элементарными магнитными массами
m1 и m2 или заряженными частицами в однородной
изотропной среде происходит согласно закону Кулона:
m1m2
F
r 2
• Магнитное поле от магнитной массы или же от
намагниченного тела рассматривается как поле
элементарных магнитных диполей.

4.

5.

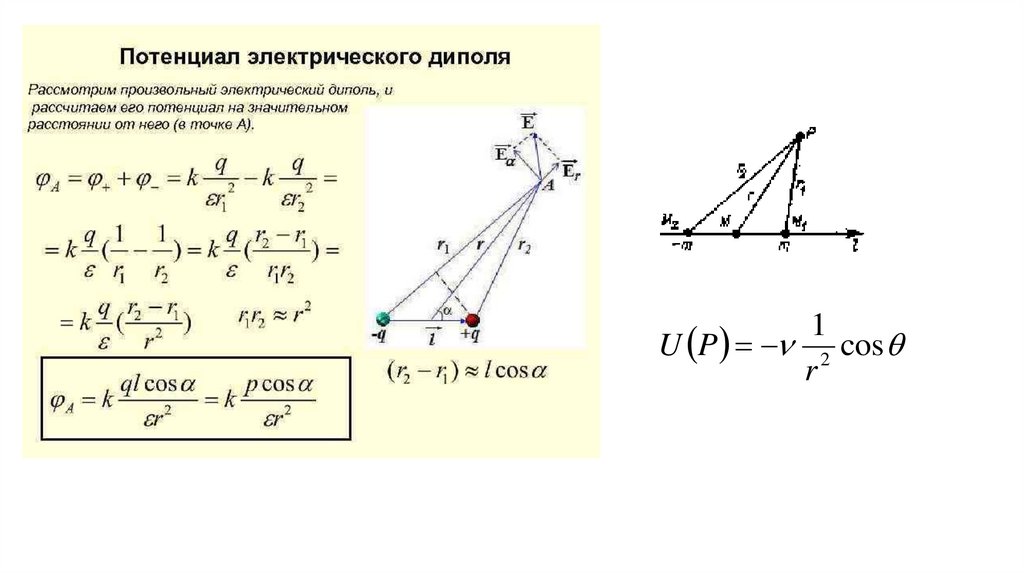
Потенциал диполя
• Пусть заданы две точки М1 и М2 , в которых расположены
равные по величине, противоположные по знаку массы m и –m.
• Линию, соединяющую эти точки, обозначим через - и
называем осью диполя. За положительное направление линии
берем направление от отрицательной массы к положительной.
• Расстояние между двумя точками М1М2 – обозначим через - d
и называем длиной диполя.
• Точка М делит расстояние М1М2 пополам, ее называем
центром диполя.
• Массы m и -m являются- полюсами диполя.
• Плоскость перпендикулярная к линии и проходящая через
точку М – называется экваториальной плоскостью.

6.

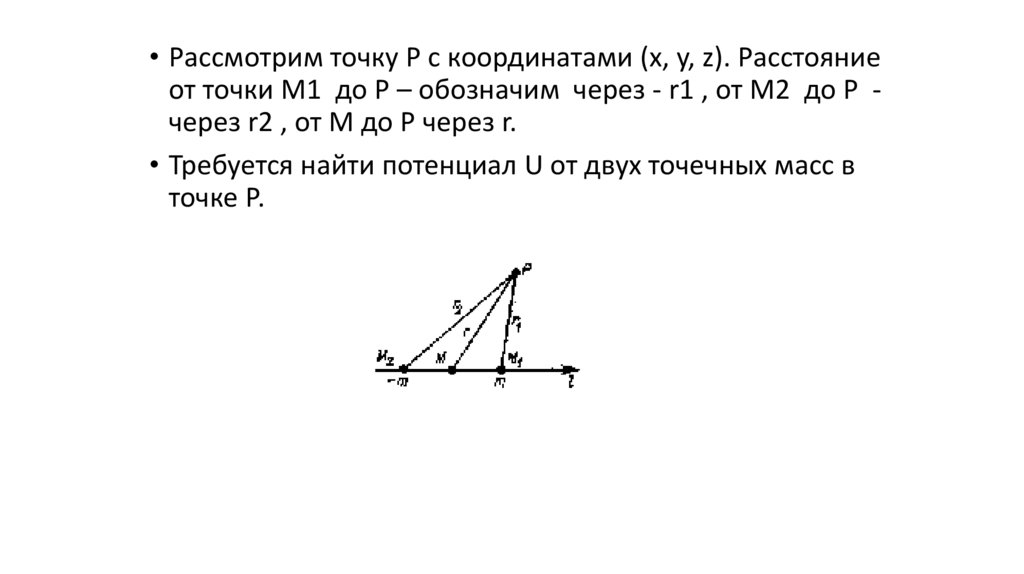
• Рассмотрим точку Р с координатами (x, y, z). Расстояние
от точки М1 до Р – обозначим через - r1 , от М2 до Р через r2 , от М до Р через r.
• Требуется найти потенциал U от двух точечных масс в
точке Р.

7.

• Применяя формулу потенциала от системы точечных масс,
находим:
m m
1 1
U P m
r1 r2
r1 r2
• Разделив и умножив правую часть этого равенства на d,
получим:
U P md
1 1
r1
r2
d
• В пределе, когда d ,0 выражение
1 1
r1
r2 дает
d
значение производной функции 1/r по направлению ; т.к. d
лежит на оси диполя .

8.

1 / r 1
1 / r1 1 / r2
lim d 0
lim
d
r
d 0
преобразуя
данную
следующее выражение:
производную,
получим
1 1 r
1
1
2 cos r , 2 cos
r r r
r
r
.
- угол между r и

9.

• Подставив полученное выражение в первоначальную
формулу, учитывая
, получим выражение
lim md
d 0
потенциала диполя :
1
U P 2 cos
r
Величина ν – называется моментом диполя
Магнитный положительной момент диполя - направлен
.
всегда в сторону массы, абсолютная
величина момента
диполя равна произведению массы положительного
полюса на длину диполя.
Итак, потенциал диполя убывает обратно
пропорционально квадрату расстояния r , зависит
от угла отклонения радиуса – вектора r от
направления момента диполя.

10.

11.

1
U P 2 cos
r

12.

Потенциал притяжения двойного слоя.
• При определении потенциала двойного слоя
гравитационные массы рассматриваются как
положительными, так и отрицательными знаками.
• Сначала рассмотрим устройство двойного слоя.
• Задана некоторая поверхность S, другие поверхности S1 и S2
расположены с обеих сторон от нее на равных расстояниях,
отсчитываемых по нормали к ней.
• Каждой точке М поверхности S на поверхностях S1 и S2
будут соответствовать точки М1 и М2 , находящиеся на одной
нормали n с точкой М .
• Расстояние М1М2 – обозначим через d, точка М делит его
пополам. На поверхности S1 и S2 расположены массы с
плотностями μ1 и μ2, причем μ1 = μ, μ2 =- μ.
• Такая совокупность поверхностных масс, распределенных на
S1 и S2 пределах при , представляет собой так называемый
двойной слой. Расстояние d называется толщиной двойного
слоя.

13.

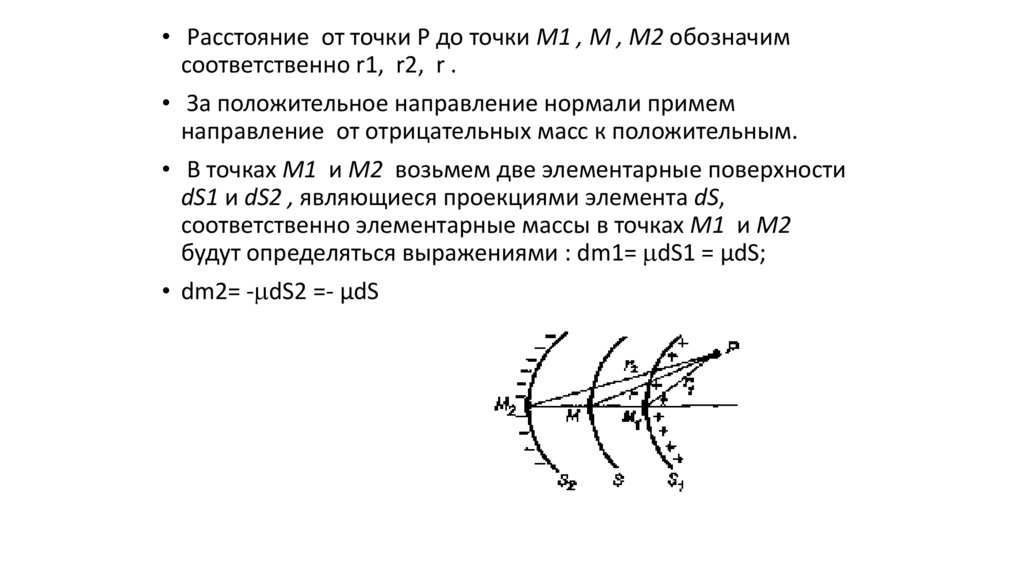
• Расстояние от точки Р до точки М1 , М , М2 обозначим
соответственно r1, r2, r .
• За положительное направление нормали примем
направление от отрицательных масс к положительным.
• В точках М1 и М2 возьмем две элементарные поверхности
dS1 и dS2 , являющиеся проекциями элемента dS,
соответственно элементарные массы в точках М1 и М2
будут определяться выражениями : dm1= dS1 = μdS;
• dm2= - dS2 =- μdS

14.

• Тогда элементы двойного слоя с центром в точке М образуют
- диполь. Момент такого диполя определяется следующим
пределом:
lim d dm lim d dS dS
• lim d плотность двойного слоя, иногда
d 0
d 0
d 0
называют моментом или мощностью двойного слоя S . β –
непрерывна во всех точках поверхности S.
Значение потенциала от рассматриваемого диполя обозначим
dV, умножая ее G – на гравитационную постоянную и
проинтегрировав его по S получим потенциал притяжения
двойного слоя:
1
V G 2 cos r , n dS
r
S

15.

Контрольные вопросы
• Устройство диполя.
• Потенциал притяжения диполя.
• Двойной слой и его потенциал притяжения