Логарифмические потенциалы. Лекция 13

1.

Логарифмические потенциалы
Лекция 13
Лектор Исаева Л.Д.

2.

План лекции
• Логарифмический потенцил притяжения
линейных масс
• Логарифмический потенциал
притяжения объемных масс
• логарифмический потенциал
притяжения простого слоя
• логарифмический потенциал диполя
• логарифмический потенциал двойного
слоя

3.

4.

Логарифмический потенцил притяжения
линейных масс
• Потенцил притяжения линейных масс имеет вид(1):
1
V P G dl
r
L
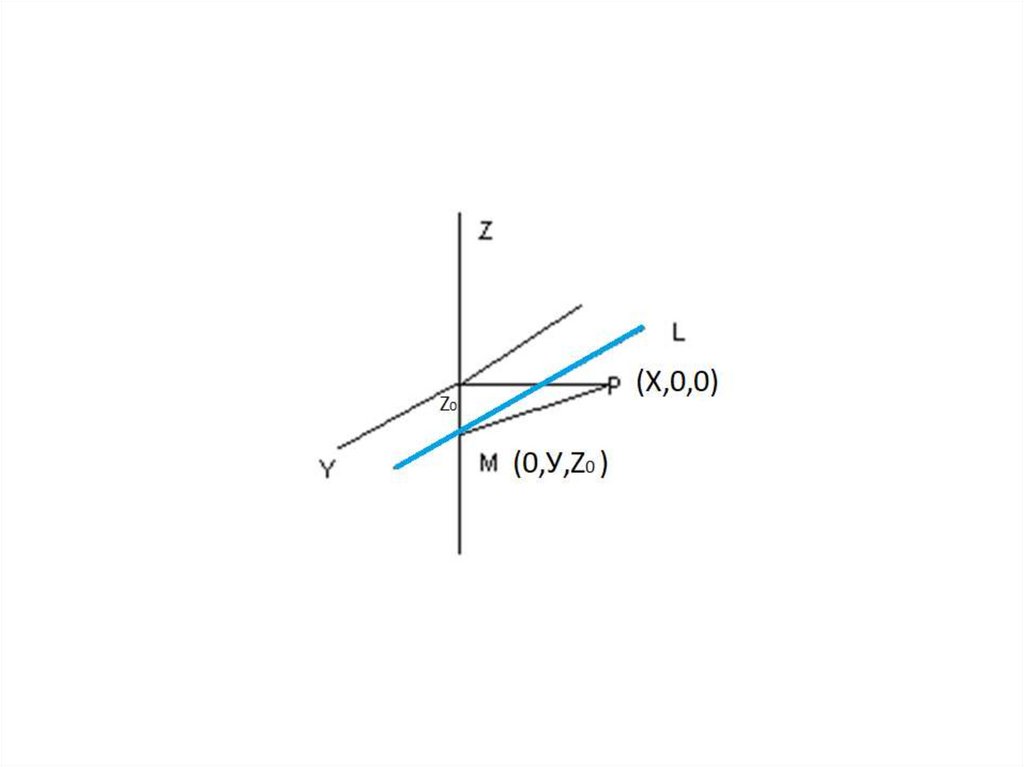
• где L- прямая с постоянной линейной плотностью λ,
залегающая на глубине и проходящая под началом
координат параллельно оси у. Элемент дуги dl=dy
рассмотрим в точке М (о,у,z0) на линии L.
• Определяем
потенциал
для
точки
Р(х,о,о),
находящейся на оси х. Расстояние между точками Р М
определяется радиус-вектором r:
r
x 2 y 2 z0
2

5.

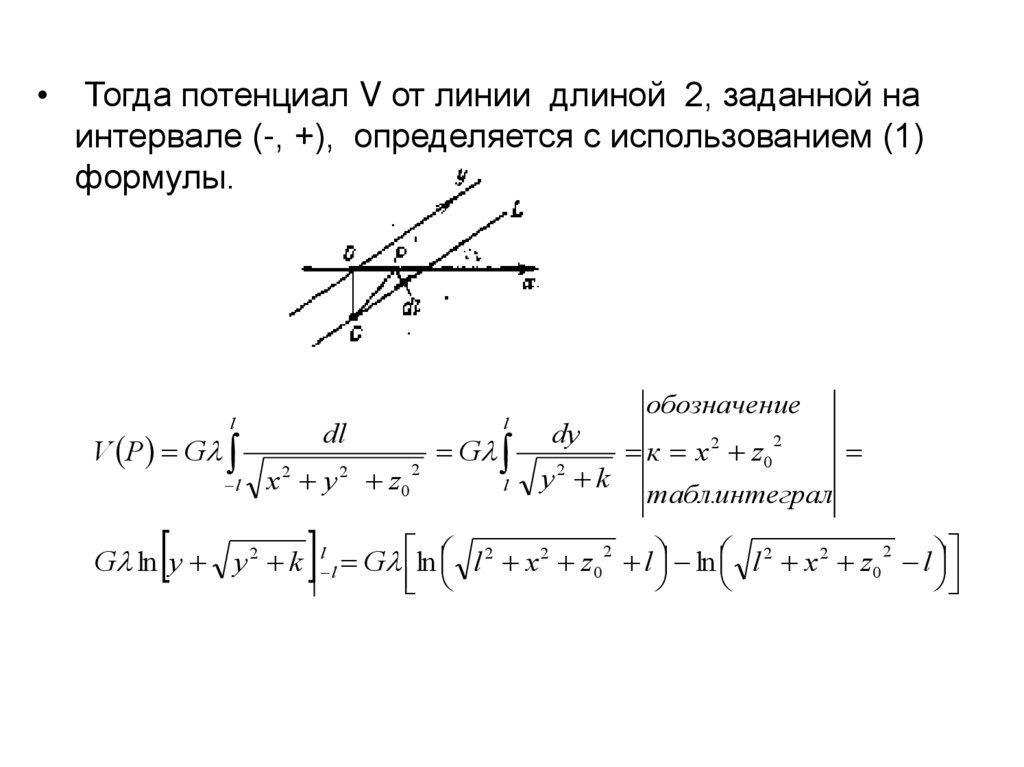
Тогда потенциал V от линии длиной 2, заданной на
интервале (-, +), определяется с использованием (1)
формулы.
l
V P G
l
G ln у
l
dl
x y
2
2
z0
2
G
l
dу
у k
2
обозначение
к х 2 z0
2
табл.интеграл
2
2
у 2 k l l G ln l 2 x 2 z0 l ln l 2 x 2 z0 l

6.

• Итак, потенциал окончательно имеет вид(2):
V P G ln
2
l 2 x 2 z0 l
2
l 2 x 2 z0 l
.
• По (2) формуле можно определить потенциал V в точке Р
от прямой линии конечной длины 2l. Рассмотрим случай
когда, тогда пользуемся приближенным значением корня:
x z0
2
2
2
l x z / 2l
2
2
0
• Тогда (2) формула имеет вид:
2l x z / 2l
V P G ln
G ln
x z / 2l
l x z / 2l l
l x 2 z 0 / 2l l
2
0
2
2
2
2
2
2
0
4l 2 x 2 z0
G ln
2
x 2 z0
2
0

7.

• Учитывая, что l x z - значением под корнем можно
пренебречь, поэтому:
2
2
0
V P G ln
4l 2
x z0
2
2
G 2 ln 2l 2G ln
1
x 2 z0
2
• Здесь при l , величина 2G λln(2l) , она постоянная,
можно ее не учитывать, т.к. практическое значение
имеет не абсолютная величина потенциала, а его
разность и градиент потенциала. Поэтому потенциал
однородной бесконечной линии или однородного
тонкого стержня, проходящего на определенной
глубине, параллельно оси у имеет вид(3):
1
V P 2G ln
r

8.

Логарифмический потенциал притяжения
объемных масс
• Задано двумерное тело с сечением S, простирающeeся
до бесконечности по направлению у. Плотность масс σ
меняется только по сечению S и является непрерывной и
конечной функцией координат точек сечения. Такое тело
можно разделить на множество бесконечных
материальных линий, направление и простирание
которых совпадает с направлением самого тела. Тогда
пологая λ=σdS из (3) получим(4):
1
V P 2G ln dS
r
S
• (4) формула определяет потенциал притяжения
бесконечного двумерного тела сечением S , который
является также логарифмическим потенциалом.

9.

10.

логарифмический потенциал притяжения
простого слоя
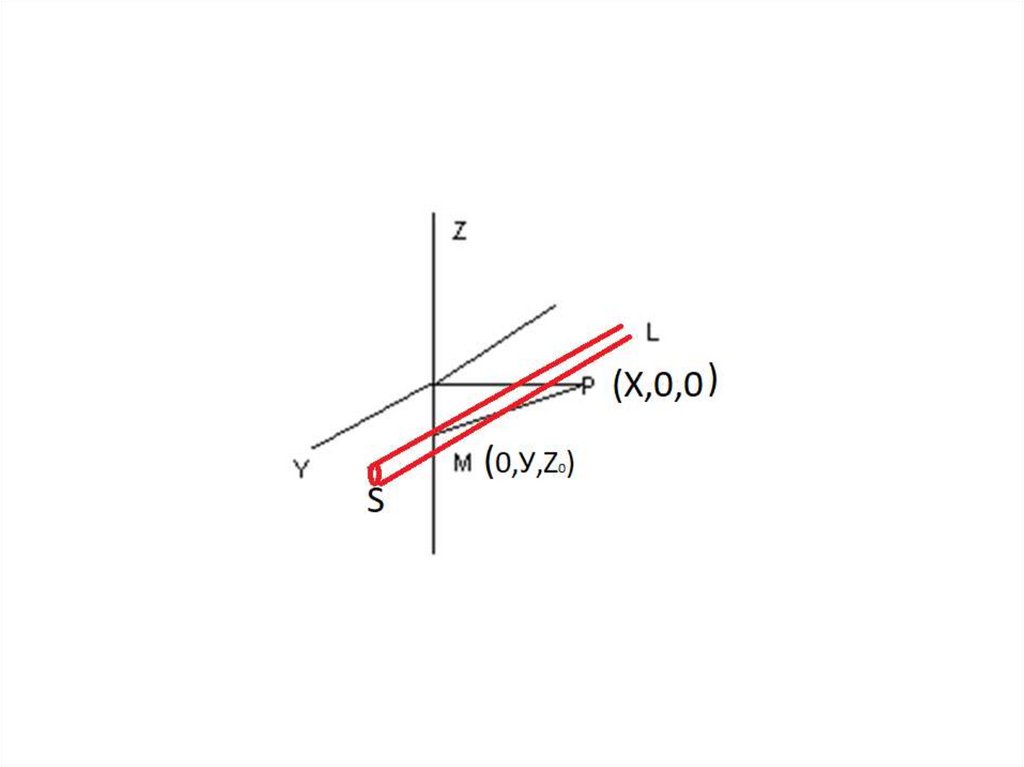
• Для определения потенциала притяжения масс,
расположенных на какой-то цилиндрической
поверхности с плотностью μ, не меняющейся по
направлению образующей, поверхность можно разбить
на полоски шириной dl и рассматривать их, как
бесконечные материальные линии с плотностью λ=μdl,
тогда на основании (3) формулы, получим(5):
1
V P 2G ln d
r
• (5) – формула определяет логарифмический потенциал
притяжения плоского простого слоя. Линия l может быть
не замкнутой . Этот потенциал удовлетворяет уравнению
Лапласа вне и внутри области, ограниченной контуром l.

11.

г)логарифмический потенциал диполя
• Диполь и двойной слой для полей с логарифмическим
потенциалом называют плоскими, в отличие
от
объемных.
Плоский
диполь
образуют
две
расположенные близко друг другу, параллельные линии
1 и 2, с массами разного знака. Потенциал притяжения
точки Р массами линий 1 и 2 в соответствии (3)
формулой имеет вид:
1
1
V P 2G ln ln
r2
r1

12.

• Умножим и делим правую часть выражения на d – длину
диполя, в пределе когда d→0. Найдем:
1
ln 1 / r1 ln 1 / r2
V P 2G lim ( d )
2Gp ln
d 0
d
n r
( d )
• Здесь P lim
-момент диполя, направленный от
d 0
отрицательной линии к положительной или(6):
1 r
1
V P 2Gp ln
2Gp cos
r r n
r
• φ – угол между направлениями r ,n;
• (6) формула определяет логарифмический потенциал
притяжения диполя.

13.

г)логарифмический потенциал притяжения
двойного слоя
• Плоский двойной слой может образоваться из плоских
диполей, если их расположить на цилиндрическую
поверхность таким образом, чтобы положительные
массы оказались с одной стороны поверхности, а
отрицательные – с другой. Тогда элементарную полоску
поверхности можно рассматривать как плоский диполь с
моментом dp=τdl, τ- момент плоской единичной
ширины. Тогда потенциал такого диполя имеет вид:
d
dV 2G cos
r
• Проинтегрировав получим логарифмический потенциал
двойного слоя (7):
1
V 2G cos d
r

14.

Контрольные вопросы
• 1) Логарифмический потенцил
притяжения линейных масс.
• 2) Логарифмический потенциал
притяжения объемных масс
• 3) Логарифмический потенциал
простого слоя.
• 4) Логарифмический потенциал диполя.
• 5) Логарифмический потенциал
двойного слоя.