Виды потенциалов притяжения (лекция 11)

1.

Виды потенциалов притяжения
Лекция 11
Лектор Исаева Л.Д.

2.

План лекции
• Потенциал притяжения точечной массы
• Потенциал притяжения системы
точечных масс.
• Потенциал притяжения объемных масс
• Потенциал притяжения простого слоя.

3.

4.

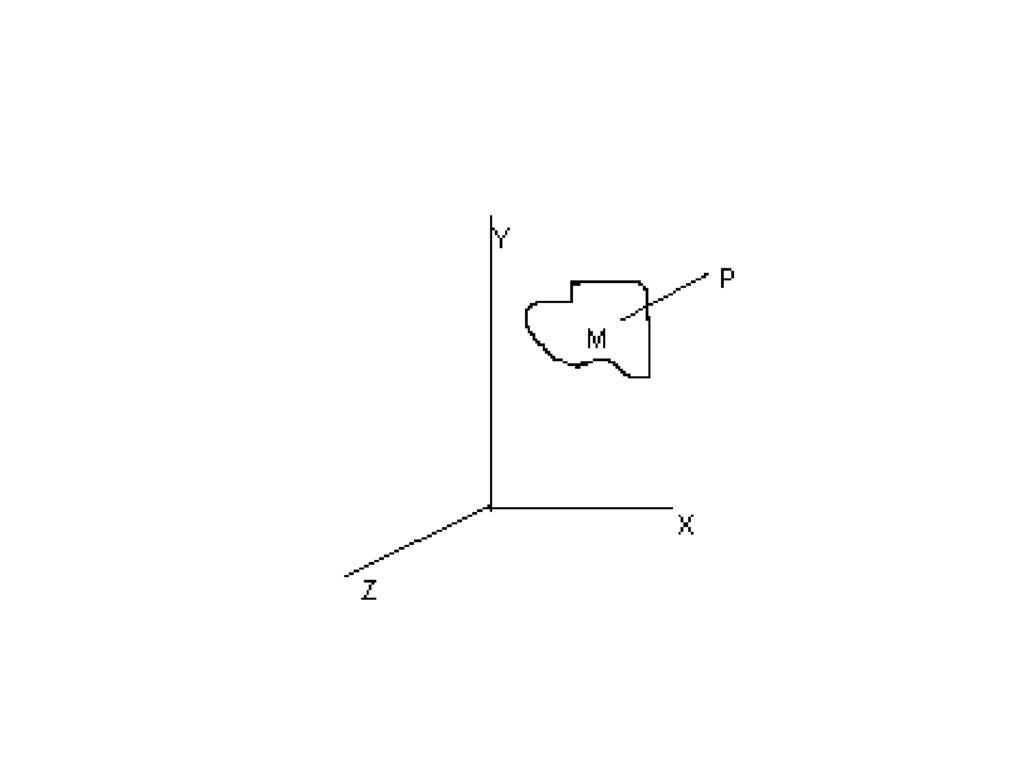
Потенциал притяжения точечной массы
• Пусть задана область пространства V,
ограниченная замкнутой поверхностью S.
Точку с координатами х0, у0, z0 в области V
обозначим через М. Будем считать, что точка
М принадлежит массам и является центром
притяжения, назовем ее притягивающей.
Любая другая точка Р с координатами х, у, z,
подвергается действию сил, тогда она
является притягиваемой. Точка Р может
находиться внутри поверхности, на ней или
вне области.

5.

• Направленный отрезок, соединяющий
точки М и Р, называется радиусвектором.
• За положительное направление радиусвектора r принимается направление от
точки М к точке Р, тогда величина радиус
- векторa определяется выражением:
r
x x0 y y 0 z z 0
2
2
2
r x x0 i y y0 j z z0 k

6.

• Сила притяжения рассматривается как вектор,
приложенный к точке P , и направленный к точке
М. Следовательно, сила притяжения и радиусвектор лежат на одной прямой, но имеют
противоположные направления.
• Косинусы углов между направлениями силы
притяжения и координатных осей
называются направляющими косинусами, и
они определяются следующими выражениями:
x x0
y y0
z z0
cos
, cos
, cos
.
r
r
r

7.

• Если в точке М находится частица с массой m, а
в точке Р единичная масса, тогда на точку Р по
закону Ньютона действует сила, численно
равная (1):
F Gm | r 2
• Знак минус учитывает, что, Fи r направлены по
одной линии, но в противоположные стороны.
• Силовое поле - потенциальное, следовательно,
вектор этого поля определяется
как градиент от
скалярной функции, т.е.(2) F gradV

8.

• Скалярную функцию V называем скалярным
потенциалом поля или потенциалом
притяжения.
• Проекции этих векторов между собой равны:
V
V
V
FX
, FY
, FZ
x
y
z
• Отсюда исходим, что потенциал поля
определяется через проекции силы
притяжения(3):
V FX dx FY dy FZ dz

9.

• Данная формула приведет к определению проекции по
осям координат :
x x0
Gm x x0
FX F cos( F , х) F cos( r x) 2
Gm 3
r
r
r
y y0
Fy Gm 3
r
z z0
FZ Gm 3
r
• Тогда потенциал поля притяжения точечной массы
определяется следующим образом:
V FX dx FY dy FZ dz
=
x x0 d ( x х0 ) ... Gm d x x0 2 y y0 2 z z0 2 Gm dr 2 Gm r 2 dr Gm
Gm
r3
2
r3
2 r3
r

10.

• Следовательно, потенциал точечной массы
определяется выражением(4)
Gm
V
r
• Исходя из этого (4) выражения, приходим к выводу, что
потенциал притяжения точечной массы
является функцией обратно пропорциональной
расстоянию r.
• Этот потенциал соответствует векторному
полю:
mr
F G 2
r r
• Во всем пространстве, за исключением точки М,
функция V удовлетворяет уравнению Лапласа, ΔV=0.

11.

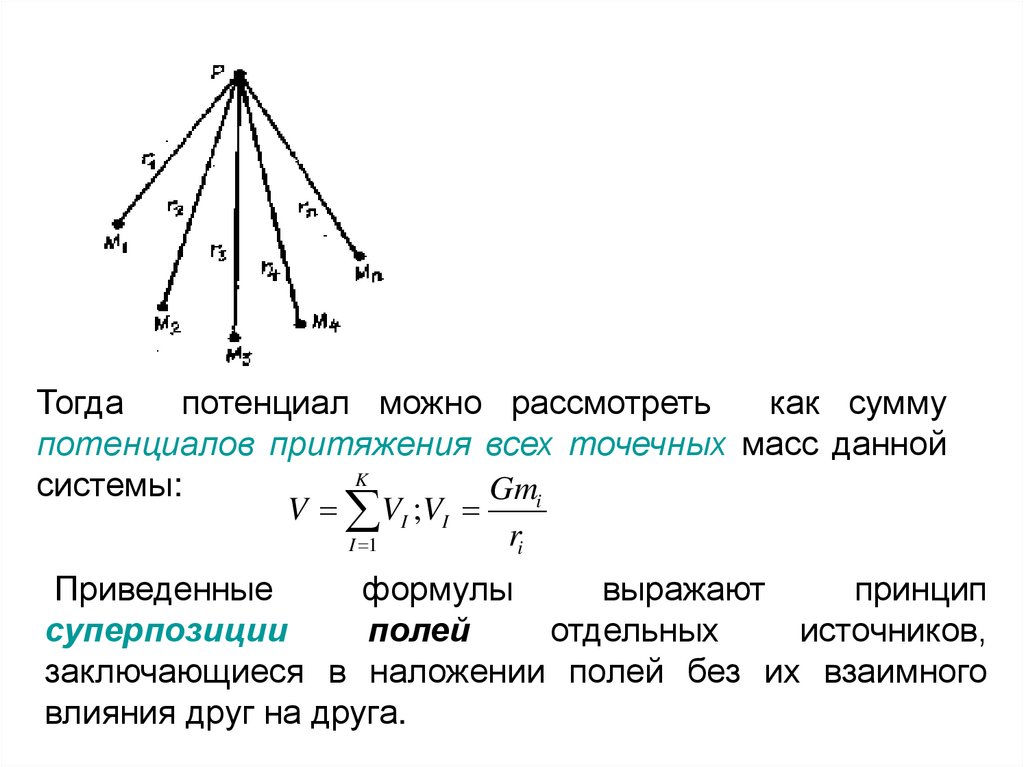
Потенциал притяжения системы
точечных масс.
1. Задано некоторое конечное число к точек M1… Mk с
заключенными в них массами m1, m2 …m k Пусть
также r1 r2… rk - расстояния от некоторой
фиксированной точки Р. В точке Р заключена
единичная масса. Тогда по закону Ньютона от точки
Мi на точку Р действуют силы F1, F2, …F k. По
правилу сложения сходящих сил
равнодействующая этих сил численно равна:
л
F Fi
i 1

12.

Тогда
потенциал можно рассмотреть
как сумму
потенциалов притяжения всех точечных масс данной
K
системы:
Gmi
V VI ;VI
ri
I 1
Приведенные
формулы
выражают
принцип
суперпозиции
полей
отдельных
источников,
заключающиеся в наложении полей без их взаимного
влияния друг на друга.

13.

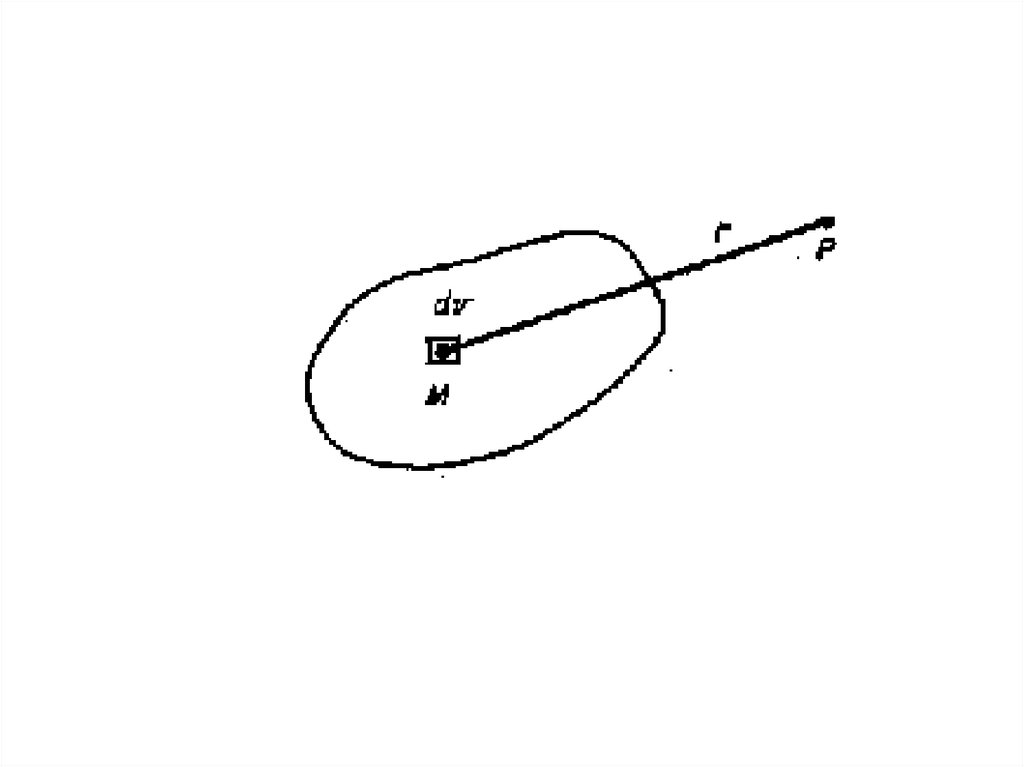
в) Потенциал притяжения объемных масс.
• Рассмотрим случай, когда притягивающая
система состоит из бесконечного множества
материальных точек, т.е. представляет собой
непрерывно протяженное материальное
тело.
• Пусть внутри области и находится сплошное
распределение масс. Плотность масс не
меняется от точки к точке, обозначим через σ.
• Тогда масса, заключенная в объеме dV
определяется выражением: dm = σ dV.

14.

15.

• Принимая элемент объема за материальную
точку, совпадающую с точкой М, обладающей
массой dm, получим потенциал притяжение
элементарного объема:
dm
dV G
r
• Заменив каждый элемент объема материальной
точкой, получим систему неподвижных
материальных точек. Их потенциал в сумме
определяет потенциал притяжения объемных
масс.
dm
d
V P G
G
r
r

16.

г) Потенциал притяжения простого слоя.
• Допустим, что действующие массы сосредоточены на
поверхности S (она может быть замкнутой или не
замкнутой) в виде слоя незначительной толщины h.
Пусть dS – элемент поверхности слоя. Поверхностная
плотность распределения масс на S равна μ. Если к
такому слою можно применить формулу потенциала
притяжения точечной массы и при заданных условиях
получим интеграл по поверхности:
dS
V P G S
r
s

17.

• Эта функция носит название потенциал
притяжения простого слоя, лежащего
на поверхности S. Выражение
потенциала притяжения простого слоя
широко применяется в гравиразведке при
определении силы тяжести от различных
материальных полос.

18.

д) Потенциал притяжения линейных масс.
• Если задано тело, двумя размерами которого можно
пренебречь по сравнению с третьим, массу такого
тела можно считать линейной, т.е. распределенной
вдоль какой-то линии L. В этом случае, где dl –
элемент дуги (линии), плотность масс - , и она
называется линейной плотностью тела.
• Для заданных таким образом масс из выражения
потенциала притяжения точечной массы получим
интеграл по длине линии:
.
dl
V P G
r
r

19.

Контрольные вопросы
• Потенциал притяжения точечной массы.
• Потенциал притяжения системы материальных точек,
принцип суперпозиции.
• Потенциал притяжения объемных масс, их свойства.
• Потенциал притяжения линейной и поверхностной
масс.
• Взаимосвязь потенциала притяжения с проекциями
силы притяжения.