Similar presentations:
Прикладная математика и математическая логика. 1 семестр
1.
Прикладная математика иматематическая логика
1 семестр
каф. МЕН
Аношина О.В.
2.
Основная литература• 1. Шипачев В. С. Высшая математика. Базовый курс: учебник и
практикум для бакалавров [Гриф Минобразования РФ] / В. С.
Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. - Москва :
Юрайт, 2015. - 447 с.
• 2. Шипачев В. С. Высшая математика. Полный курс: учебник для акад.
бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А. Н. Тихонова. - 4е изд., испр. и доп. - Москва : Юрайт, 2015. - 608 с
• 3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в
упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я.
Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.
• 4. Кремер Н. Ш., Путко Б.А., Гришин И.М., Фридман М.Н. Высшая
математика для экономистов [Электронный ресурс]: учебник для
вузов [Гриф Минобразования РФ] / [Н. Ш. Кремер и др.]; под ред. Н.
Ш. Кремера. - 3-е изд. - Электрон. текстовые дан. - Москва: ЮНИТИДАНА: Закон и право, 2015. - 479с.
3.
Отчетность1.
Контрольная работа №1 (рабочая программа, стр. 16-21, задачи с 1
по 6 включительно). Выполняется в соответствии:
Рабочая программа дисциплины «ПРИКЛАДНАЯ МАТЕМАТИКА И
МАТЕМАТИЧЕСКАЯ ЛОГИКА». Рос. гос. проф.-пед. ун-т. Екатеринбург,
2017. 38 с.
Вариант контрольной работы выбирать по последней цифре номера
зачетной книжки.
2.
Дифференцированный зачет
4.
Элементы математической логикиТермин "логика" происходит от древнегреческого logos,
означающего
"слово, мысль, понятие, рассуждение, закон".
Основатели математической логики:
– греческий философ
Аристотеля (384–322 гг. до н.э.);
– немецкий математик Готфрид Вильгельм Лейбниц (1646–1716);
– швейцарский математик Леонард Эйлер (1707–1783);
– чешский математик
Бернард Больцано (1781–1848);
– английский учёный Джордж Буль (1815–1864);
– немецкий математик
Эрнест Шредер (1841–1902);
– американский математик и инженер Клод Шеннон (1916–2001)
и др.
5.
Математическая логика – это наука осредствах и методах математических
доказательств.
Алгебра логики применима к любым переменным, которые могут
принимать только два значения
(0 или 1).
Например, к состоянию контактов:
включено-выключено или напряжению (или току): есть-нет, которыми
представляется информация в ЭВМ.
6.
На практике множество элементарных логическихопераций является обязательной частью набора
инструкций всех современных микропроцессоров и
соответственно входит в языки программирования.
Это является одним из важнейших практических
приложений методов математической логики.
7.
Высказывание – это утверждение о чемлибо, которое может быть либо истинным,либо ложным.
Примеры высказываний:
1. Новгород стоит на Волхове.
2. Париж – столица Англии.
3. Карась не рыба.
4. Число 6 делится на 2 и на 3.
5. Если юноша окончил среднюю школу, то он получает аттестат зрелости.
8.
Истинные и ложные высказывания1. "Все учащиеся русской школы программистов
умеют говорить по-русски".
2. "Основные предметы, преподаваемые в школе
программистов – это, конечно, живопись и
чистописание".
9.
Повелительные, вопросительные, восклицательныеи бессмысленные предложения не являются
высказываниями
-«Уходя, гасите свет!»
- «Да здравствует мыло душистое и полотенце
пушистое!»
- «Который час?»
- «Привет нашим спортсменам!»
10.
Высказывание, представляющее собой одно утверждениепринято называть простым.
Сложное высказывание получается путем объединения
простых высказываний, связанных – союзами И, ИЛИ и
частицей НЕ.
Логическая функция – это функция, устанавливающая
соответствие между одним или несколькими
высказываниями, которые называются аргументами
функции, и высказыванием, которое называется
значением функции.
11.
Булевойфункцией
y=f(x1,x2,…,xn)
от
п
переменных x1,x2,...,xn называется любая функция, в
которой аргументы и функция могут принимать
значение либо 0 либо 1, т.е. булева функция это
правило, по которому произвольному набору нулей
и единиц x1,x2,...,xn ставится в соответствие значение
0 или 1.
12.
Отрицание (инверсия) .Говорят, что имея суждение А, можно образовать новое суждение, которое
читается как «не А» или «неверно, что А».
A
Запись ¬А,
А
A
1
0
0
1
Пример.
Высказывание А : Сегодня по расписанию будут занятия по математике.
Высказывание A
: Сегодня по расписанию не будет занятий по математике
или неверно, что сегодня по расписанию будут занятия по математике.
Высказывание A : Неверно, что сегодня по расписанию не будет занятий
по математике.
13.
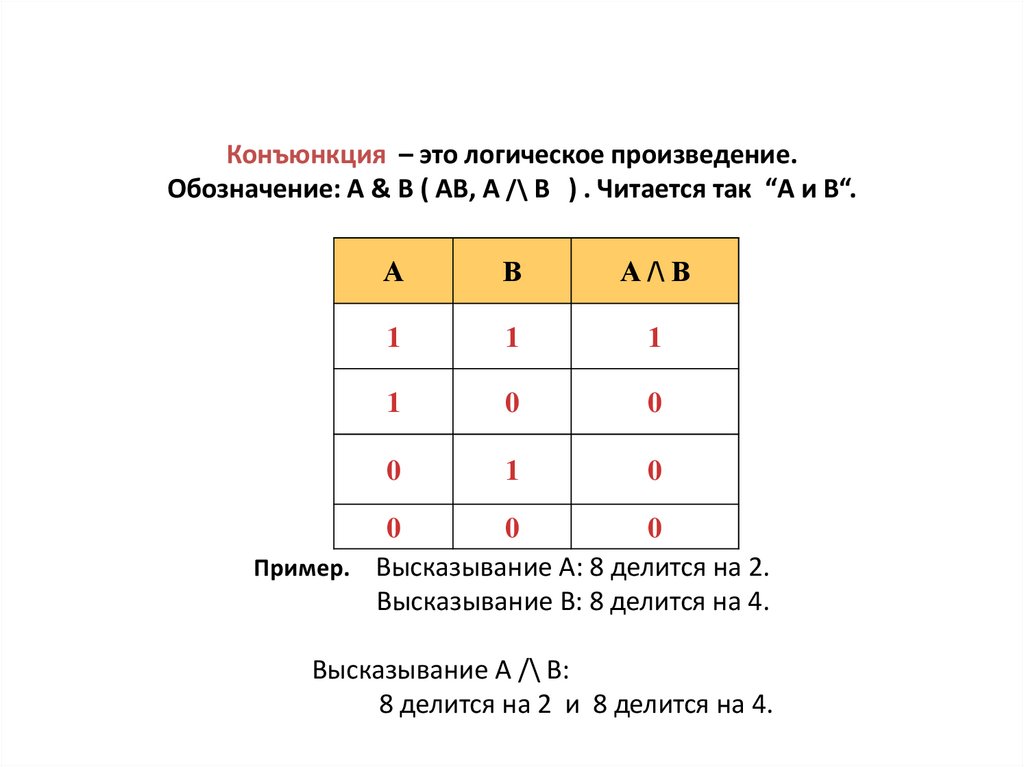
Конъюнкция – это логическое произведение.Обозначение: А & В ( АВ, А /\ В ) . Читается так “А и В“.
А
В
А /\ В
1
1
1
1
0
0
0
1
0
0
0
0
Пример. Высказывание А: 8 делится на 2.
Высказывание В: 8 делится на 4.
Высказывание А /\ В:
8 делится на 2 и 8 делится на 4.
14.
Дизъюнкция – это логическое сложение.Обозначение: А \/ В, ( А + В ). Читается так: “ А или В ”.
А
В
А \/ В
1
1
1
1
0
1
0
1
1
0
0
0
Пример. Высказывание А:
Высказывание В:
Москва – столица России.
Киев
– столица России.
Высказывание А \/ В:
Москва – столица России или Киев – столица России.
15.
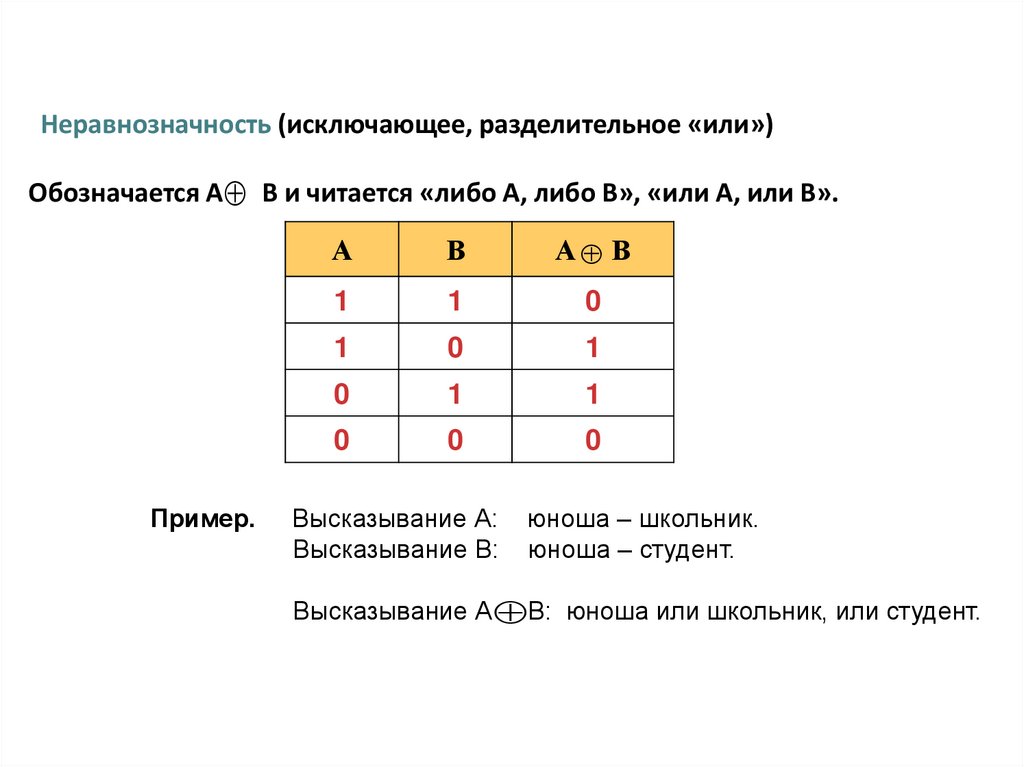
Неравнозначность (исключающее, разделительное «или»)Обозначается А В и читается «либо А, либо В», «или А, или В».
Пример.
А
В
А В
1
1
0
1
0
1
0
1
1
0
0
0
Высказывание А:
Высказывание В:
юноша – школьник.
юноша – студент.
Высказывание А В: юноша или школьник, или студент.
16.
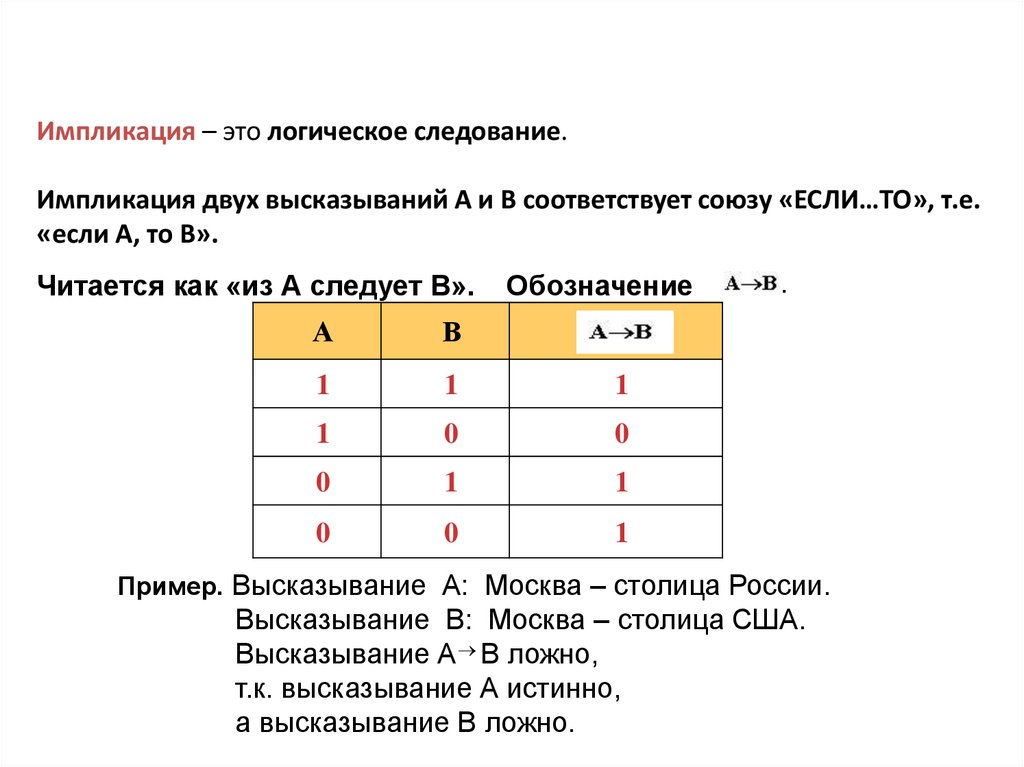
Импликация – это логическое следование.Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО», т.е.
«если А, то В».
Читается как «из А следует В».
Обозначение
А
В
1
1
1
1
0
0
0
1
1
0
0
1
.
Пример. Высказывание А: Москва – столица России.
Высказывание В: Москва – столица США.
Высказывание А В ложно,
т.к. высказывание А истинно,
а высказывание В ложно.
17.
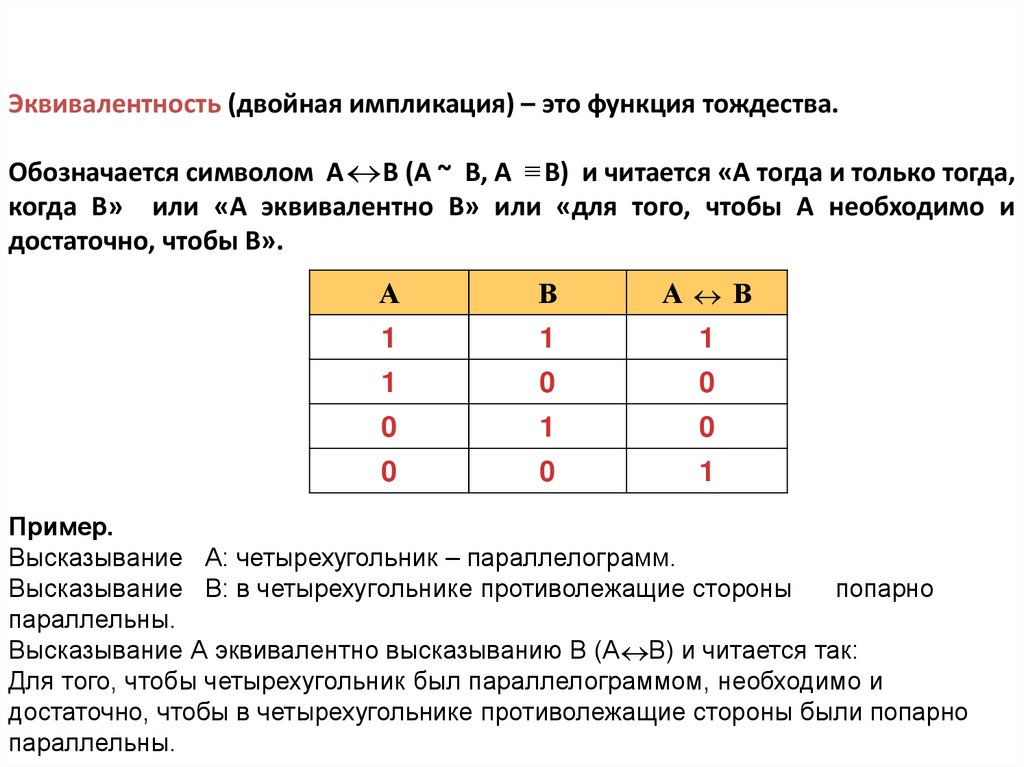
Эквивалентность (двойная импликация) – это функция тождества.Обозначается символом А В (А ~ В, А В) и читается «А тогда и только тогда,
когда В» или «А эквивалентно В» или «для того, чтобы А необходимо и
достаточно, чтобы В».
А
В
А В
1
1
1
1
0
0
0
1
0
0
0
1
Пример.
Высказывание А: четырехугольник – параллелограмм.
Высказывание В: в четырехугольнике противолежащие стороны
попарно
параллельны.
Высказывание А эквивалентно высказыванию В (А В) и читается так:
Для того, чтобы четырехугольник был параллелограммом, необходимо и
достаточно, чтобы в четырехугольнике противолежащие стороны были попарно
параллельны.
18.
С помощью алгебры логики над высказываниями можно выполнятьследующие операции:
1) из заданной совокупности элементарных высказываний строить
различные сложные высказывания;
2) сложные высказывания представлять в виде цепочки элементарных
высказываний;
3) упрощать ложные высказывания с помощью равносильных формул;
4) проверять (доказывать) истинность или ложность цепочек сложных
высказываний.
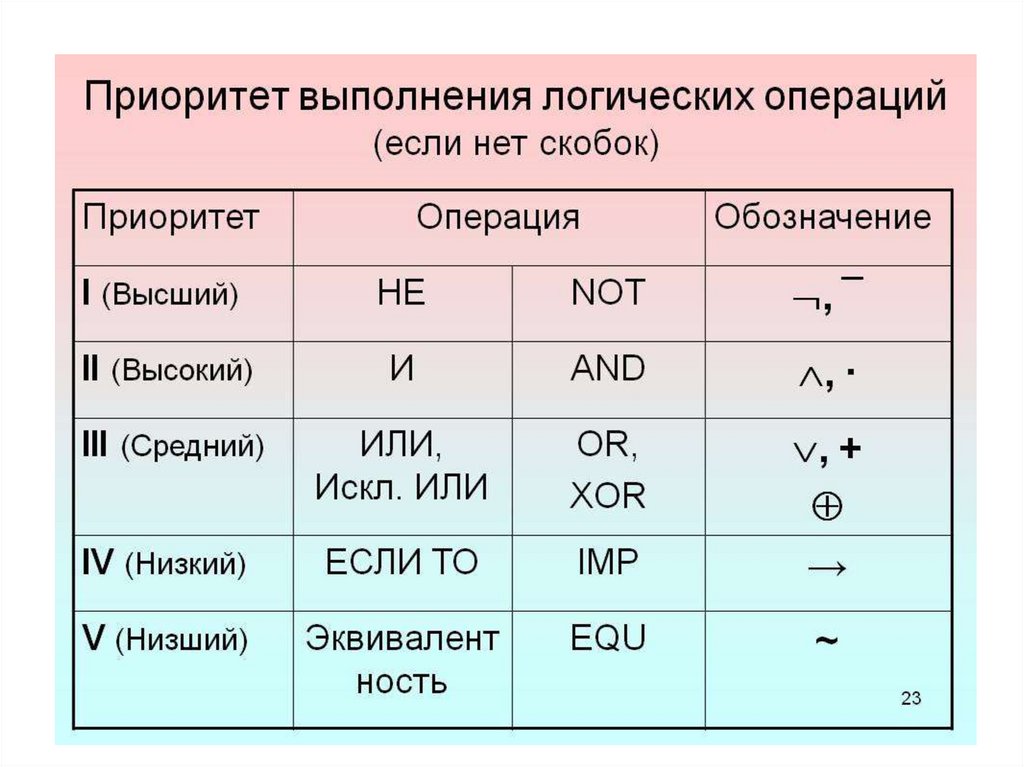
19.
Порядок выполнения операций указывается скобками,которые можно опускать, придерживаясь следующего
порядка действий:
• конъюнкция выполняется раньше, чем все остальные
операции;
•дизъюнкция – раньше, чем импликация и эквивалентность;
• если над формулой стоит знак отрицания, то скобки тоже
опускаются.
20.
СПАСИБОЗА ВНИМАНИЕ!
21.
Пример. Записать логической цепочкой следующее сложное высказывание:«Если спортсмен интенсивно тренируется и
при этом принимает запрещенные стимуляторы, то
он достигает высоких спортивных результатов либо
попадается на допинге».
Решение. Данное сложное высказывание состоит из следующих простых:
А – спортсмен интенсивно тренируется;
В – спортсмен принимает запрещенные стимуляторы;
С – спортсмен достигает высоких спортивных результатов;
D – спортсмен попадается на допинге.
(А /\ В) (С D).
22.
Переведем на язык алгебры логики следующее высказывание:1. «Я поеду в Москву, и если встречу там друзей, то мы интересно проведем
время».
Введем следующие простые высказывания:
М – «я поеду в Москву»;
В – «встречу там друзей»;
И – интересно проведем время».
2. «Если я поеду в Москву и встречу там друзей, то мы интересно
проведем время».
23.
3. «Если будет солнечная погода, то ребята пойдут в лес, а если будетпасмурная погода, то ребята пойдут в кино».
Введем следующие простые высказывания:
С – «солнечная погода»;
Р – «ребята пойдут в лес»;
К – «ребята пойдут в кино».
24.
4. Если у меня будет свободное время и я сдамэкзамены по педагогике и психологии, то я поеду
отдыхать в Крым или на Кавказ.
25.
Интегральное исчислениефункций одной переменной
Первообразная и неопределенный
интеграл
Определение. Функция F x называется
первообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
первообразной функции sin x , так как
cos x sin x .
26.
Очевидно, если F x - первообразнаяфункции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
27.
Определение. Совокупность всехпервообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .
28.
Если F x - некоторая первообразная функцииf x , то пишут f x dx F x C , хотя
правильнее бы писать f x dx F x C .
Мы по устоявшейся традиции будем писать
f x dx F x C .
Тем самым один и тот же символ
f x dx будет обозначать как всю
совокупность первообразных функции f x ,
так и любой элемент этого множества.
29.
Свойства интегралаПроизводная неопределенного интеграла равна
подынтегральной функции, а его дифференциалподынтегральному выражению. Действительно:
1.( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2.d f ( x)dx ( f ( x)dx) dx f ( x)dx.
30.
Свойства интеграла3. Неопределенный интеграл от
дифференциала непрерывно ( x )
дифференцируемой функции равен самой
этой функции с точностью до постоянной:
d ( x) ( x)dx ( x) C ,
так как (x ) является первообразной для (x).
31.
Свойства интеграла4.Если функции f1 x и f 2 x имеют
первообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
32.
Таблица неопределенных интегралов1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
33.
Таблица неопределенных интегралов11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
dx
x
arcsin C ..
a
a2 x2
14.
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
C .
15. 2 2 ln
2
a
a
x
a x
16.
dx
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
19.
dx
thx C .
2
ch x
dx
20. 2 cthx C .
sh x
34.
Свойства дифференциаловПри интегрировании удобно пользоваться
свойствами: 1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3
35.
ПримерыПример . Вычислить cos 5xdx .
Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
36.
ПримерыПример. Вычислить x 3x x 1 dx .
2
3
Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4 x2
3
x C
3
4
2
37.
Независимость от вида переменнойПри вычислении интегралов удобно
пользоваться следующими свойствами
интегралов:
Если f x dx F x C , то
f x b dx F x b C .
Если f x dx F x C , то
1
f ax b dx F ax b C .
a
38.
ПримерВычислим
1
6
(
2
3
x
)
dx
(
2
3
x
)
C
.
3 6
5
39.
Методы интегрированияИнтегрирование по частям
Этот метод основан на формуле udv uv vdu .
Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
40.
ПримерыПример. Вычислить x cos xdx .
Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
41.
ПримерыПример. Вычислить
dx
x2
x 2 dx
x
ln x
=
x ln xdx
2
2
2 x
x
dv xdx, v
2
u ln x, du
x2
1
x2
1 x2
ln x xdx
ln x
C .
=
2
2
2
2 2
42.
Метод замены переменнойПусть требуется найти f x dx , причем
непосредственно подобрать первообразную
для f x мы не можем, но нам известно, что
она существует. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t t dt , где x t , а t - новая
переменная
43.
Интегрирование функций, содержащихквадратный трехчлен
Рассмотрим интеграл
ax b
dx ,
x px q
содержащий квадратный трехчлен в
знаменателе подынтегрального
выражения. Такой интеграл берут также
методом замены переменных,
предварительно выделив в
знаменателе полный квадрат.
2
44.
ПримерВычислить
dx
.
x 4x 5
Решение. Преобразуем x 2 4 x 5 ,
2
выделяя полный квадрат по формуле a b 2 a 2 2ab b 2 .
Тогда получаем :
x2 4x 5 x2 2 x 2 4 4 5
x 2 2 2 x 4 1 x 2 2 1
x 2 t
dx
dx
dt
x t 2
x 2 2 1 dx dt
x2 4x 5
t 2 1
arctgt C arctg x 2 C.
45.
ПримерНайти
1 x
1 t
x t, x t 2 ,
2tdt
1 x dx dx 2tdt
2
1 t
2
tdt
1 t
2
2
t2
1 t
2
dt
d (t 2 1)
t
2
1
2
dt
ln(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln( x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt
46.
Определенный интеграл, его основныесвойства. Формула Ньютона- Лейбница.
Приложения определенного интеграла.
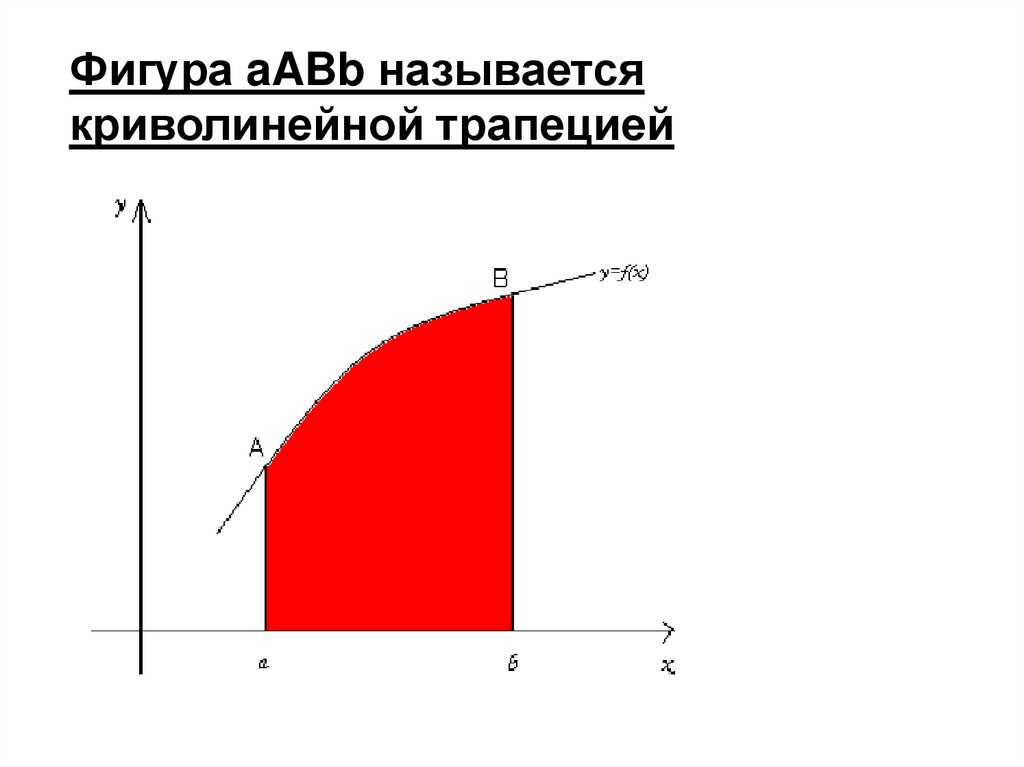
• К понятию определенного интеграла приводит
задача нахождения площади криволинейной
трапеции.
• Пусть на некотором интервале [a,b] задана
непрерывная функция y f ( x ) 0
Задача:
Построить ее график и найти F площадь фигуры,
ограниченной этой кривой, двумя прямыми x = a и x
= b, а снизу – отрезком оси абсцисс между точками
x = a и x = b.
47.
Фигура aABb называетсякриволинейной трапецией
48.
Определениеb
f ( x)dx
Под определенным интегралом
a
от данной непрерывной функции f(x) на
данном отрезке [a;b] понимается
соответствующее приращение ее
первообразной, то есть
F (b) F ( a ) F ( x) /
b
a
Числа a и b – пределы интегрирования, [a;b]
– промежуток интегрирования.
49.
Правило:• Определенный интеграл равен разности
значений первообразной подынтегральной
функции для верхнего и нижнего пределов
интегрирования.
• Введя обозначения для разности
b
F (b) F (a) F ( x) / a
b
f ( x)dx F (b) F (a)
a
Формула Ньютона – Лейбница.
50.
Основные свойства определенногоинтеграла.
1)Величина определенного интеграла не зависит от
обозначения переменной интегрирования, т.е.
b
b
a
a
f ( x)dx f (t )dt
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми
пределами
интегрирования равен нулю
a
f ( x)dx F (a) F (a) 0
a
51.
3) При перестановке пределов интегрированияопределенный интеграл меняет свой знак на обратный
b
a
f ( x)dx F (b) F (a) F (a) F (b) f ( x)dx
a
b
(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число
частичных промежутков, то определенный интеграл,
взятый по промежутку [a;b], равен сумме определенных
интегралов, взятых по всем его частичным промежуткам.
b
c
b
f ( x)dx f ( x)dx f ( x)dx
c
a
a
52.
5)Постоянный множитель можно выноситьза знак определенного интеграла.
6)Определенный интеграл от алгебраической
суммы конечного числа непрерывных
функций равен такой же алгебраической
сумме определенных интегралов от этих
функций.
53.
3. Замена переменной в определенноминтеграле.
b
f ( x)dx f (t ) (t )dt
a
a ( ), b ( ), (t ) [a; b]
где
для t [ ; ] , функции (t ) и (t ) непрерывны на ;
5
Пример:
x 1dx
1
=
4
0
x 1 t
dt dx
=
x 1 5
t 0 4
2 32 4 2
2
16
1
t dt t 0 t t 40 4 2 0
5
3
3
3
3
3
54.
Несобственные интегралы.Определение. Пусть функция f(x) определена на
бесконечном интервале [a; + ) и интегрируется
на любом интервале [a;b], где b < + . Если
существует
b
lim
f ( x)dx,
b
a
то этот предел называется несобственным
интегралом функции f(x) на интервале
[a; + ) и обозначается
f ( x.)dx
a
55.
• Таким образом, по определению,b
f ( x)dx lim f ( x)dx lim ( F (b) F (a))
a
b
a
b
Если этот
предел некоторое
число, то
интеграл
f ( x)dx
a
называется
сходящимся, если предела не существует, или он равен ,
то говорят, что интеграл расходится.
56.
Пример. Интеграл Пуассона:e
x2
a2
dx
• если а = 1, то
e
x2
dx
• Интеграл сходится, и его значение
.
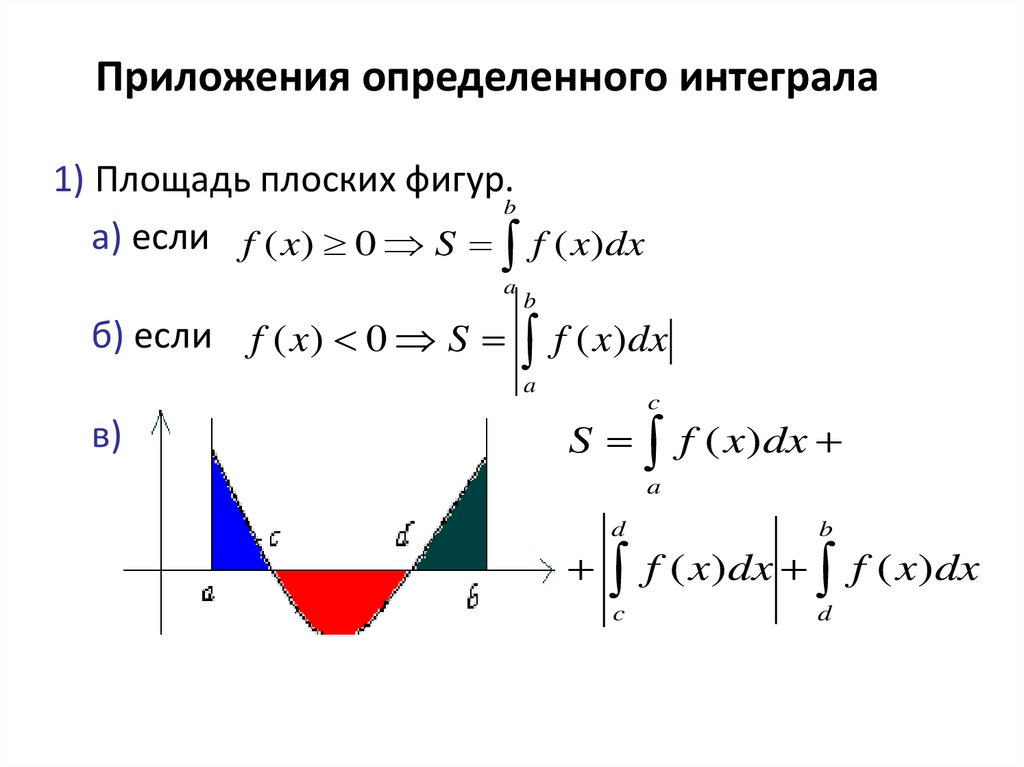
57.
5. Приложения определенного интеграла1) Площадь плоских фигур.
b
а) если f ( x) 0 S f ( x)dx
a
b
б) если f ( x) 0 S f ( x) dx
a
в)
c
S f ( x)dx
a
d
b
c
d
f ( x)dx f ( x)dx
58.
bг) S
f ( x) ( x) dx
a
2) Многие физические величины можно
определить и задать через понятие
интеграла. Например, работа для любой
силы вычисляется как интеграл от величины
b
силы по длине пути.
A F ( x)dx
a
59.
Числовые и функциональные ряды1. Основные определения
Опр. Сумма всех членов последовательности – ряд
∞






































































 mathematics
mathematics








