Similar presentations:
Знаки тригонометрических функций. Урок 3
1.
Урок 32.
3.
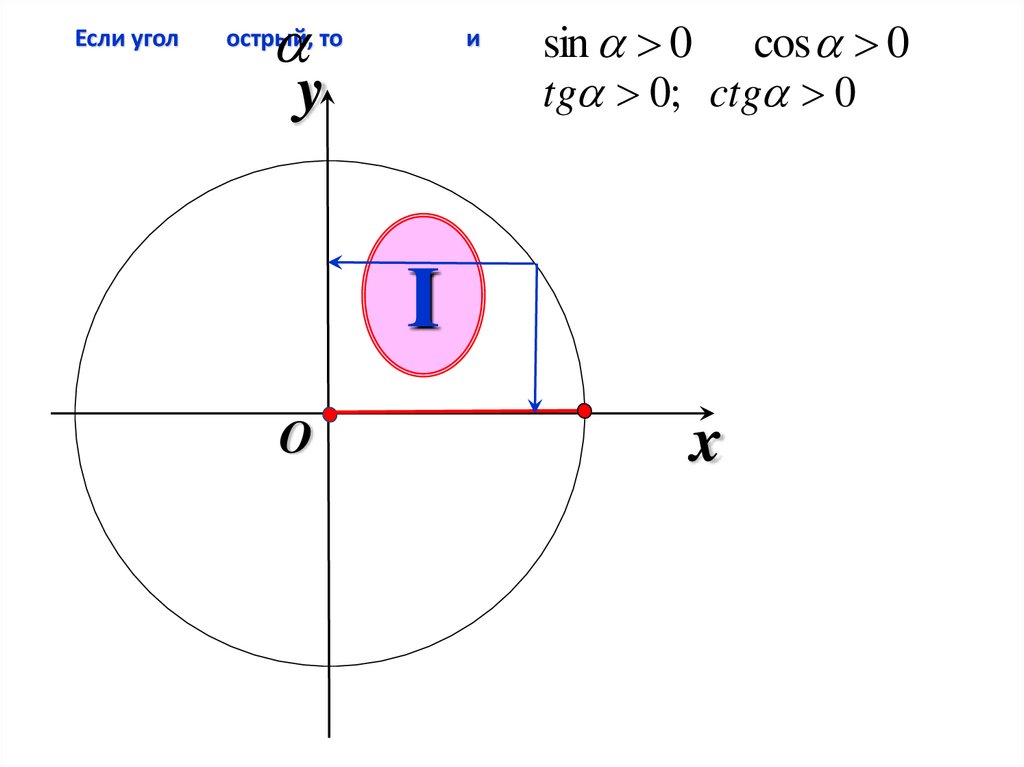
Если уголy
острый, то
и
sin 0 cos 0
tg 0; ctg 0
I
O
x
4.
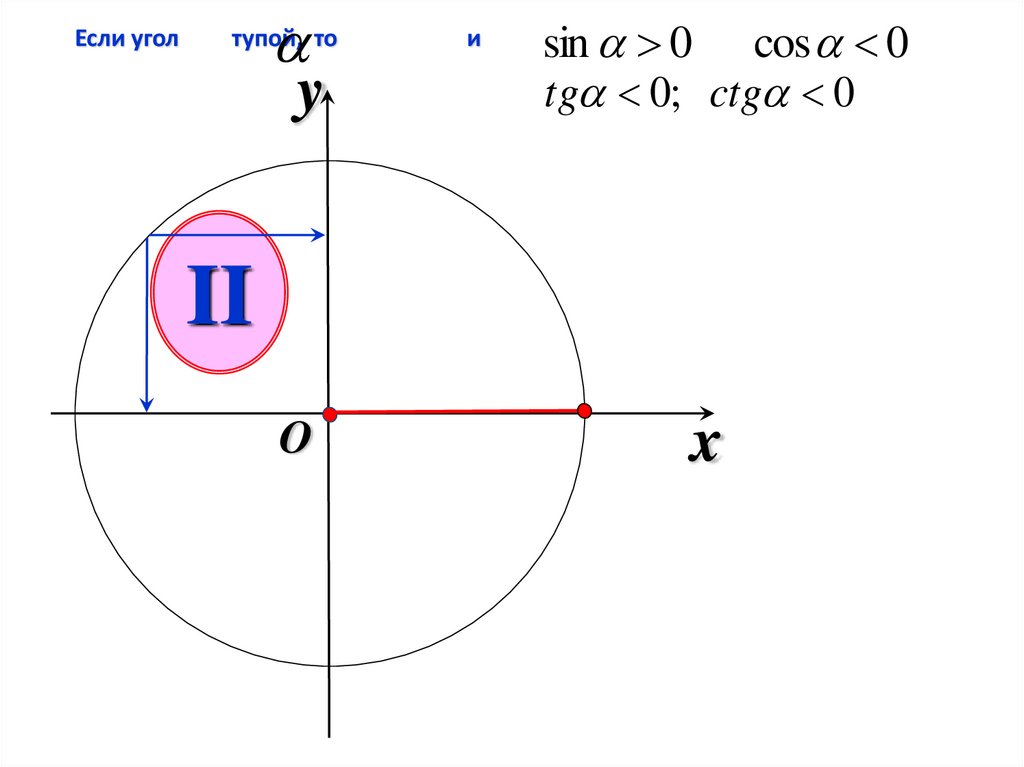
Если уголy
тупой, то
и
sin 0 cos 0
tg 0; ctg 0
II
O
x
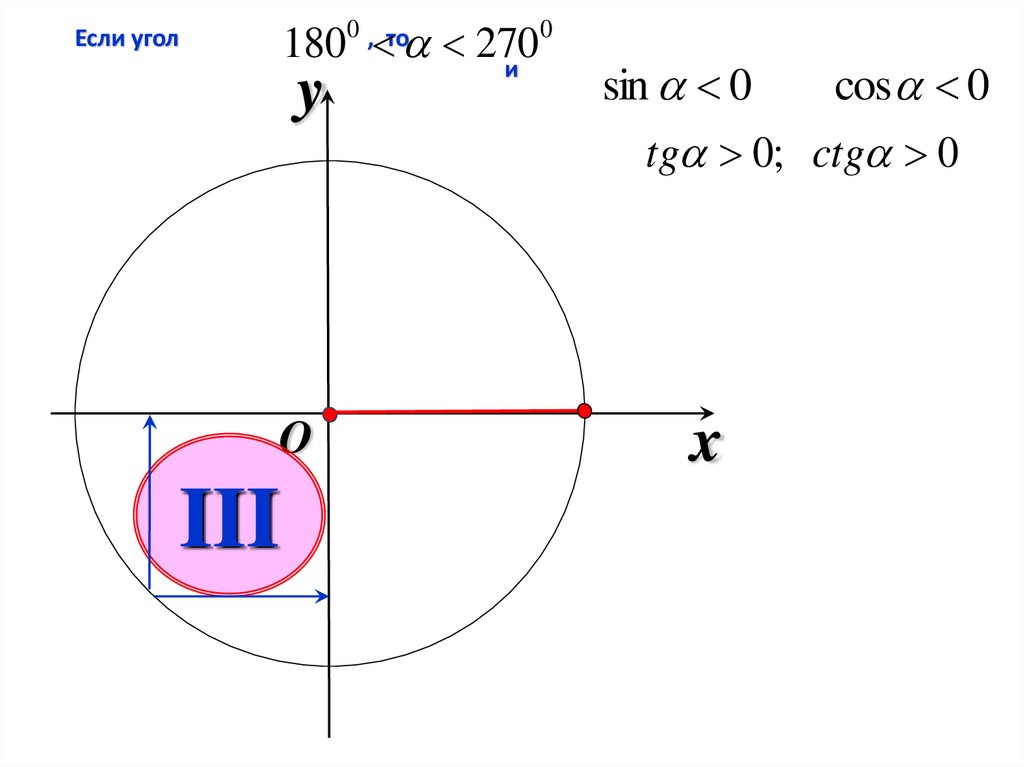
5.
180 270и
0 , то
Если угол
y
O
III
0
sin 0
cos 0
tg 0; ctg 0
x
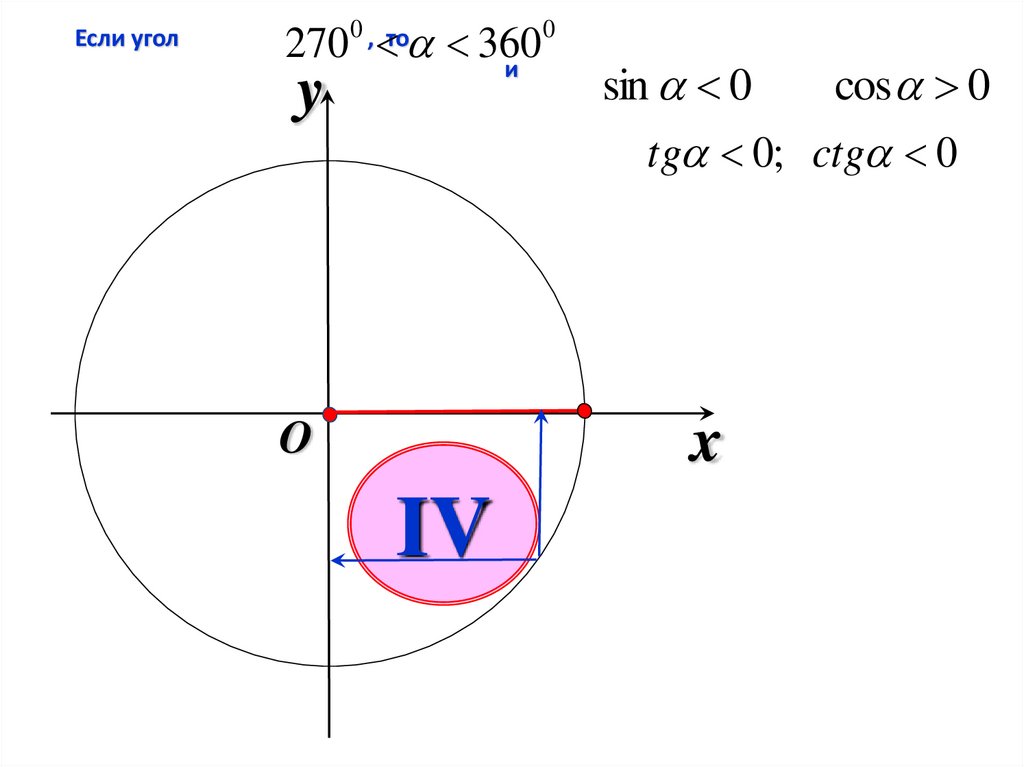
6.
Если угол270 360
и
0 , то
y
0
sin 0
cos 0
tg 0; ctg 0
x
O
IV
7.
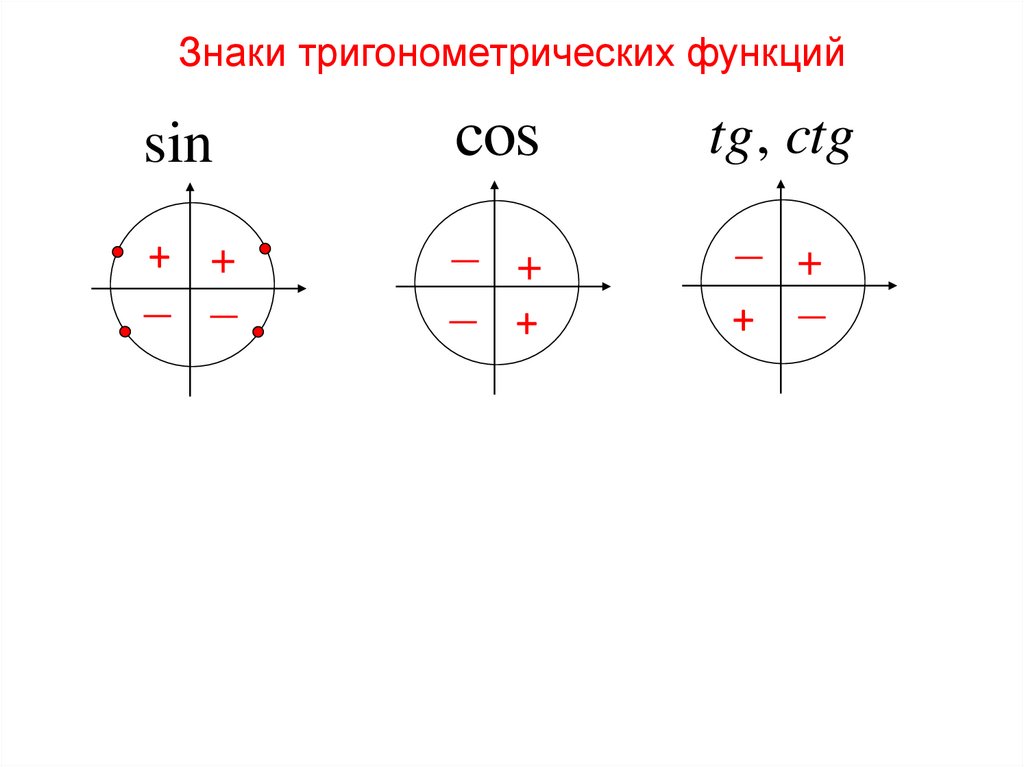
Знаки тригонометрических функцийsin
cos
tg, ctg
+ +
_ _
_
+
_ +
_
+
_
+
8.
Бланк №721 а, б
722,
724
9.
Тригонометрическая функцияЧетверть
Знак
sin 125
cos( 39 )
II
+
IV
+
sin 280
tg405
IV
-
I
+
10.
Тригонометрическая функцияЧетверть
Знак
cos177
II
-
cos( 144 )
III
-
III
ctg189
sin( 179 ) III
+
-
11.
Тригонометрическая функция+
+
sin 100 cos 300
+
sin 190 tg 200
+
+
cos 320 ctg10
Знак
+
-
+
12.
Сравните:1) sin 195 cos ( 100 ) > 0
ΙΙΙ
ΙΙΙ
-
-
ΙΙ
ΙΙ
+
-
2) sin 123 > tg123
3) cos 210 ctg ( 21 ) < 0
ΙΙΙ
ΙV
-
-
13.
Бланк № 72514.
15.
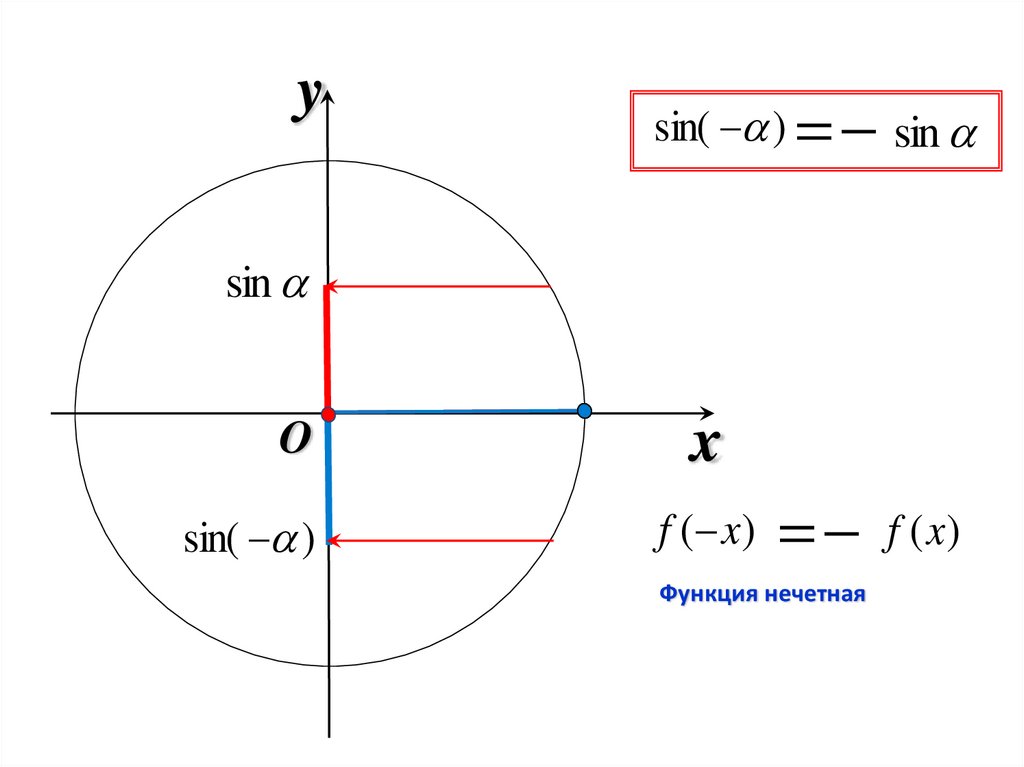
ysin( ) sin
sin
O
sin( )
x
f ( x) f (x)
Функция нечетная
16.
sintg
cos
sin
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x) f (x)
Функция нечетная
tg( ) tg
ctg( ) ctg
17.
f ( x)f (x)
Функция четная
cos( )
f ( x) f (x)
Функция нечетная
cos
sin( ) sin
tg( ) tg
ctg( ) ctg
18.
Вычислить:cos 40
1)
1;
cos 40
sin 40
2)
1;
sin 40
3) tg 65 ctg 65
tg 65 ( ctg 65 )
tg 65 ctg 65 1;
19.
14) tg ( 42 )
tg 42 tg 42
ctg 42
0
5) (cos180 cos 0 ) sin 20
( 1 1) sin 20 0 sin 20
0
20.
Тангенсы углов вычисляются по формуле:sin
tg
cos
Если
cos 0, то тангенс не существует
tg 90 не существует, т.к.
cos 90 0
tg 270 не существует, т.к.
cos 270 0
21.
0sin 180
0
tg 180
cos 180 1
0
tg 0 tg 360 0
1
22.
Котангенсы углов вычисляются по формуле:cos
сtg
sin
Если
sin 0, то котангенс не существует
ctg 180 не существует, т.к.
sin 180 0
ctg 0 не существует, т.к.
sin 0 0
23.
Р (cos ; sin )Вычислить:
у
1 х
2
2
1) cos 45 cos180
(-1) =
2
2
3
3
0=
2) sin 60 sin 360
2
2
sin 30 1
1
3)
:2
4
2
2
24.
уР (cos ; sin )
1 х
4) cos 54 cos 90 cos 54 0 0
2
2
3 2
5) cos 30 sin 45
2 2
2
2
3 2
1
1
4 4
4
25.
33
0
6) tg 30 tg180
3
3
sin 65
7)
tg 65 0
cos 65
26.
Сравните:sin 100 cos100 tg100 ctg100 < 0
+
-
-
-
Укажите наибольшее из чисел:
sin ( 10 )
cos( 10 )
tg ( 10 )
-
+
-
Ответ:
cos( 10 )











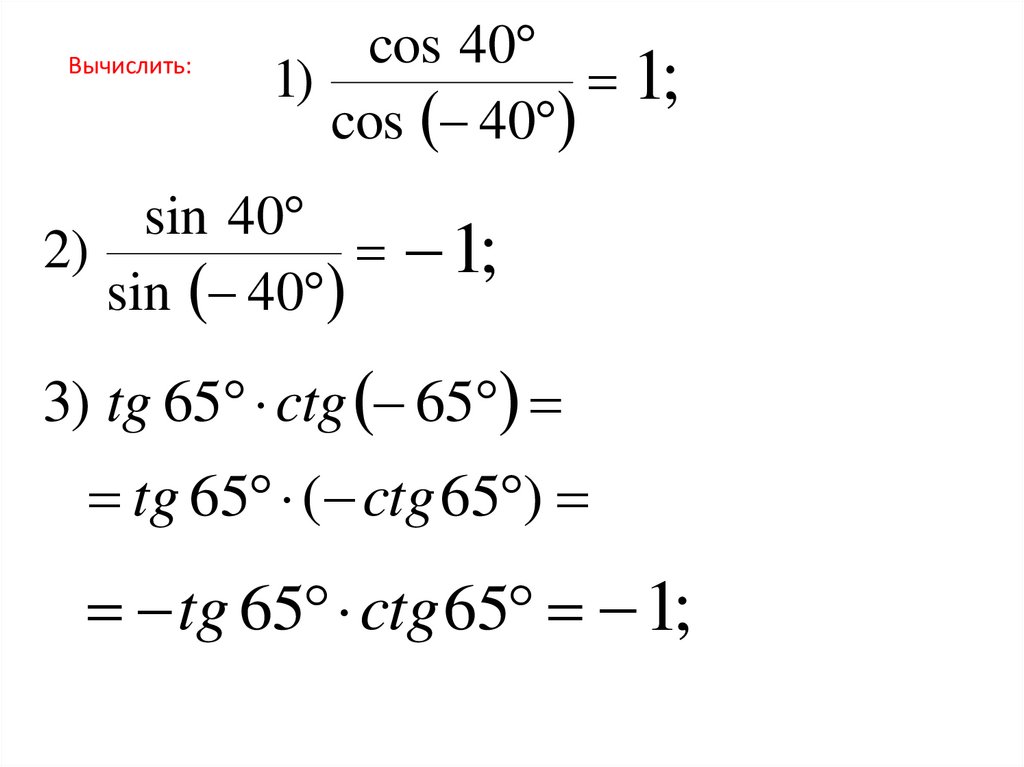
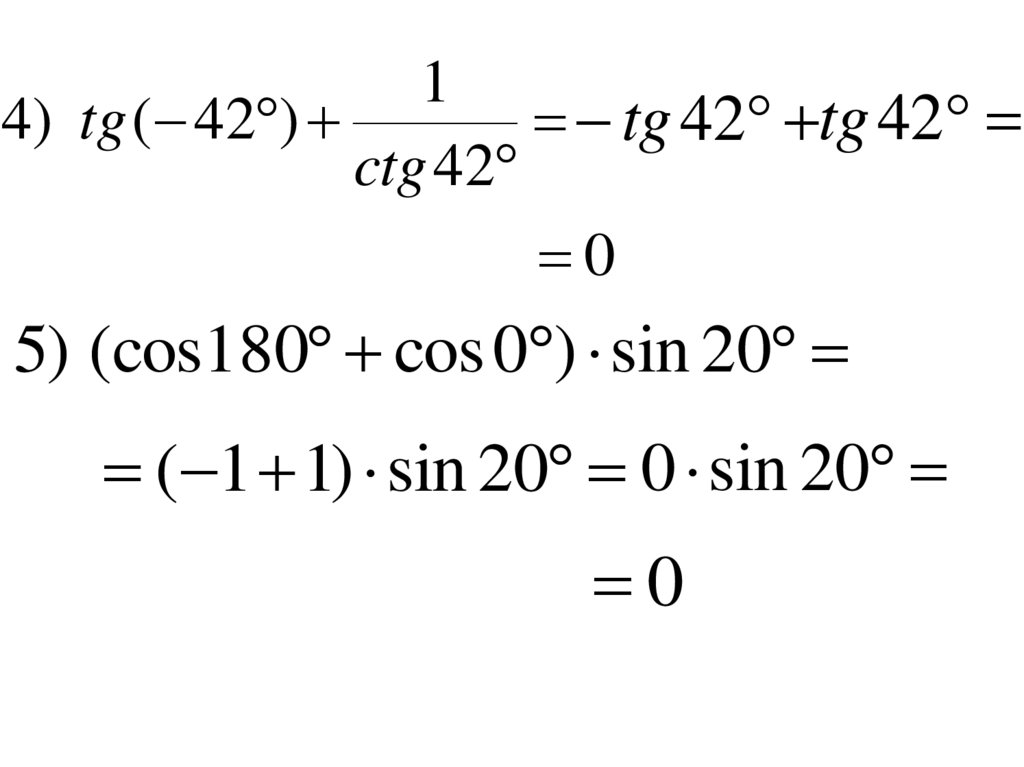

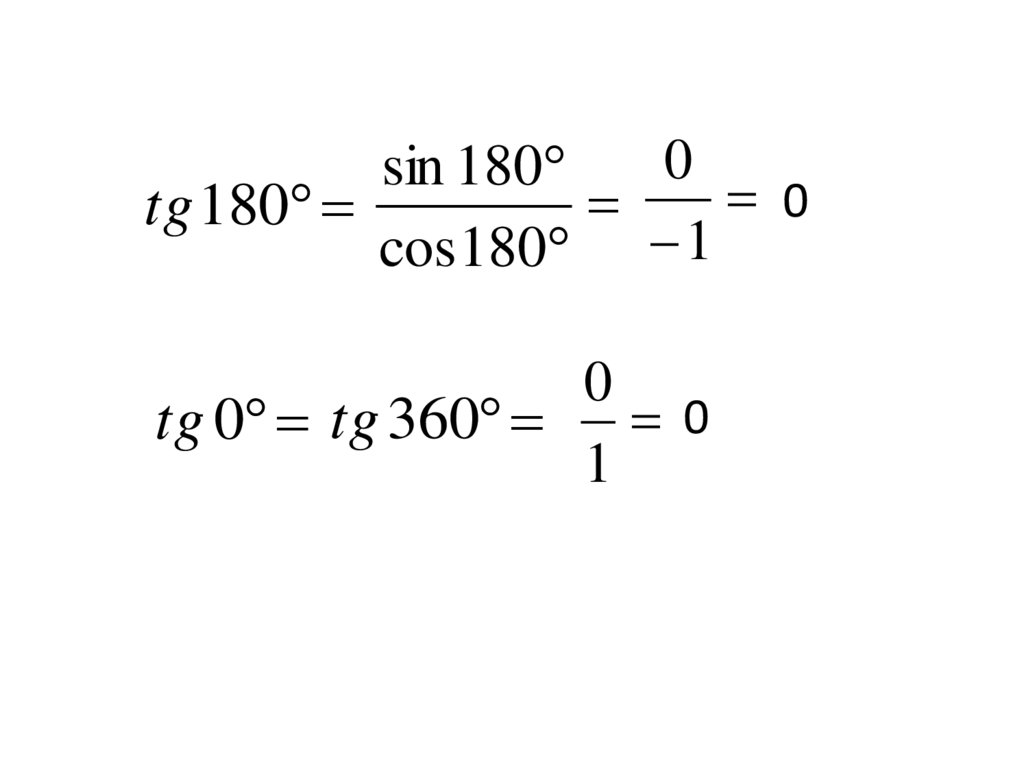


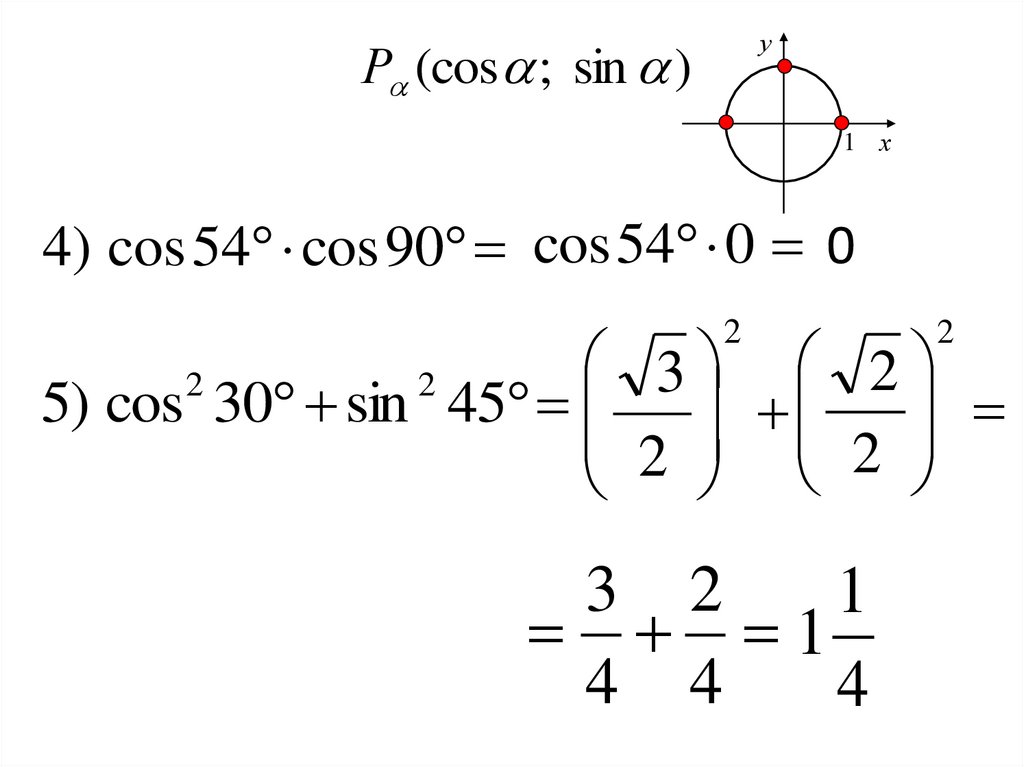
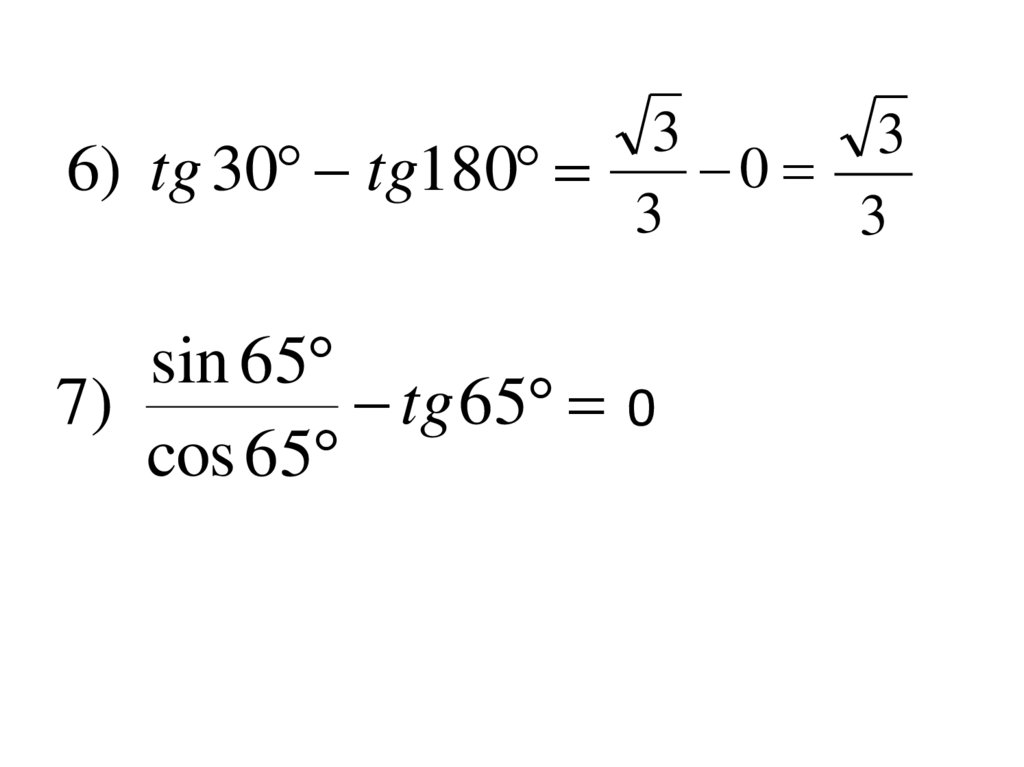
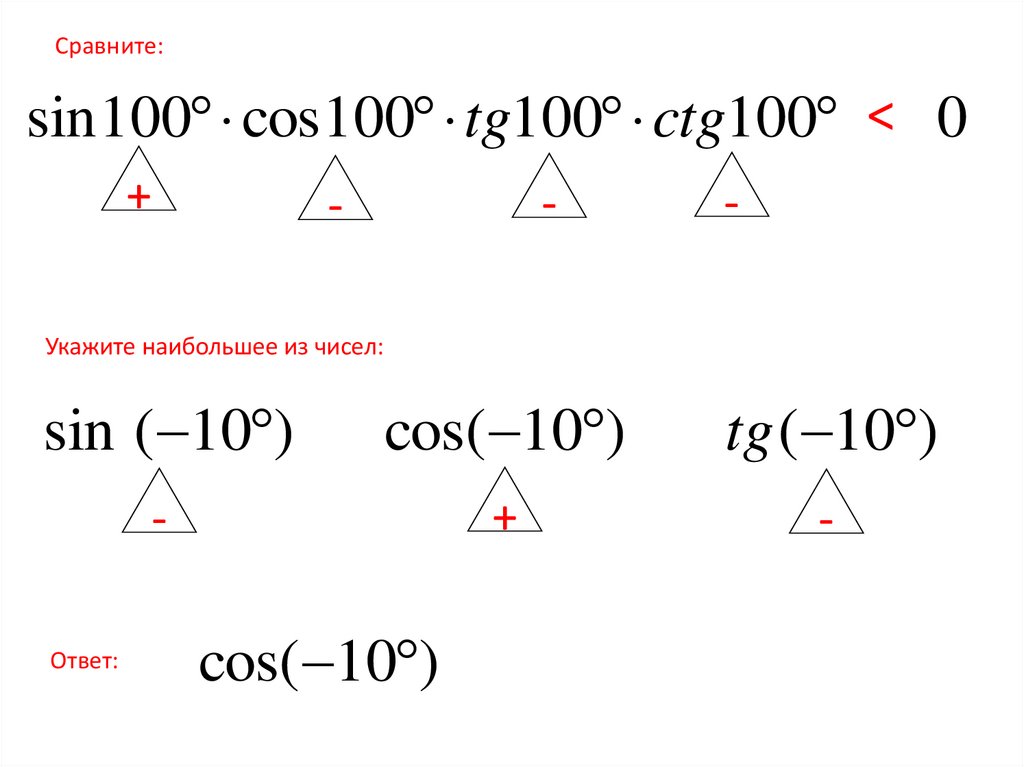

 mathematics
mathematics








