Similar presentations:
Площадь круга и его элементов (сектора и сегмента)
1. Площадь круга и его элементов (сектора и сегмента).
2. Круг – часть плоскости, ограниченная окружностью. Круг радиуса R с центром О содержит саму точку О и все точки плоскости,
находящиеся от точки О, на расстоянии, небольшем чем радиус R.
R
O
3.
Рассмотрим вписанныйправильный многоугольник.
в
окружность
Площадь данного круга будет больше площади
многоугольника, так как он полностью находится в этом круге.
Учтем также, что площадь круга, вписанного в данный
многоугольник, будет меньше площади самого
многоугольника, так как круг полностью находится в самом
многоугольнике.
Следовательно, справедливо следующее неравенство:
S'n < Sn < S (1)
4.
Радиус вписанной в многоугольник окружности рассчитывается по формуле:Предположим, что число сторон многоугольника неограниченно растёт
тогда справедливо будет выражение:
.
,
Таким образом, можно сделать вывод, что радиус вписанной окружности
стремится к радиусу описанной окружности
.
Вывод. При неограниченном увеличении числа сторон правильного
многоугольника вписанная в него окружность стремится к описанной
окружности.
Поэтому и площадь вписанного круга будет стремиться к площади описанного
круга:
при
.
5.
Для вычисления площади круга радиусом R применим формулу площадиправильного n-угольника:
, где Pn – периметр n-угольника A1 A2 An.
Принимая во внимание, что радиус вписанной окружности стремится к радиусу
описанной окружности,
периметр n-угольника также стремится к длине
окружности,
, а площадь вписанной окружности стремится к площади
описанной окружности
при
запишем формулу для вычисления
площади круга с радиусом R:
– площадь круга радиусом R.
6.
Круговой секторКруговым сектором или просто сектором
называется часть круга, ограниченная дугой и двумя
радиусами, соединяющими концы с центром круга.
Дуга, ограничивающая сектор, называется дугой
сектора.
7.
Круговой секторВыведем формулу для вычисления площади
закрашенного сектора круга радиуса R и ограниченного
дугой с градусной мерой .
Площадь всего круга:
.
Площадь кругового сектора, ограниченного дугой в 1° равна
.
Площадь S кругового сектора
с произвольным углом α будет равна:
8.
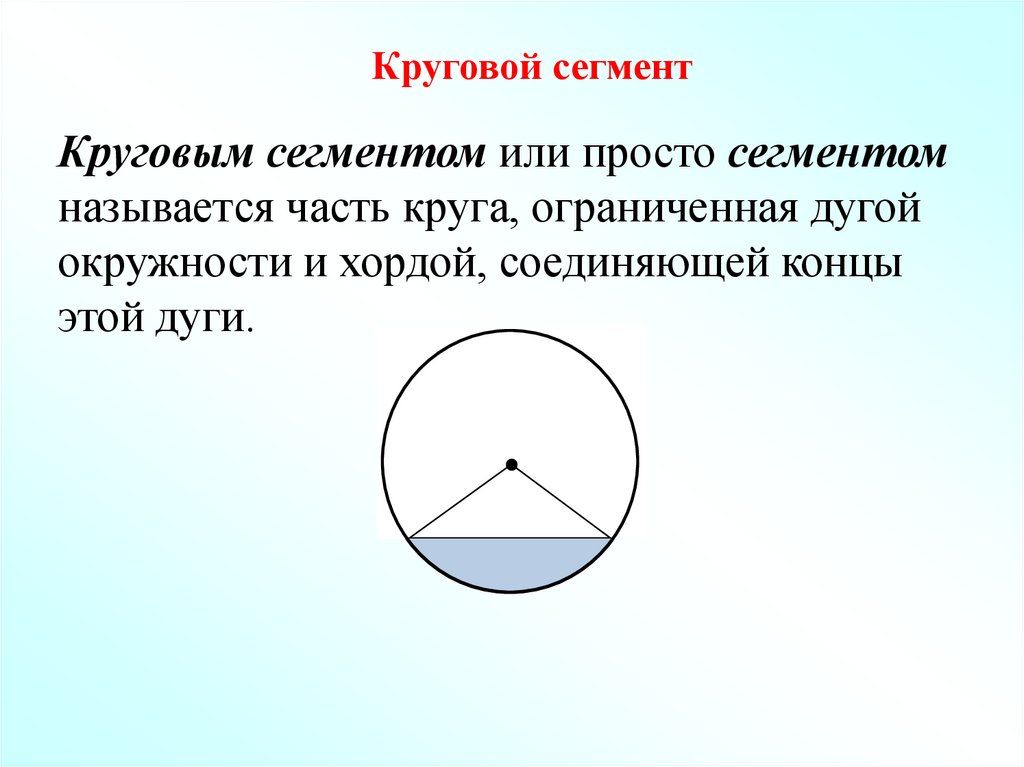
Круговой сегментКруговым сегментом или просто сегментом
называется часть круга, ограниченная дугой
окружности и хордой, соединяющей концы
этой дуги.
9.
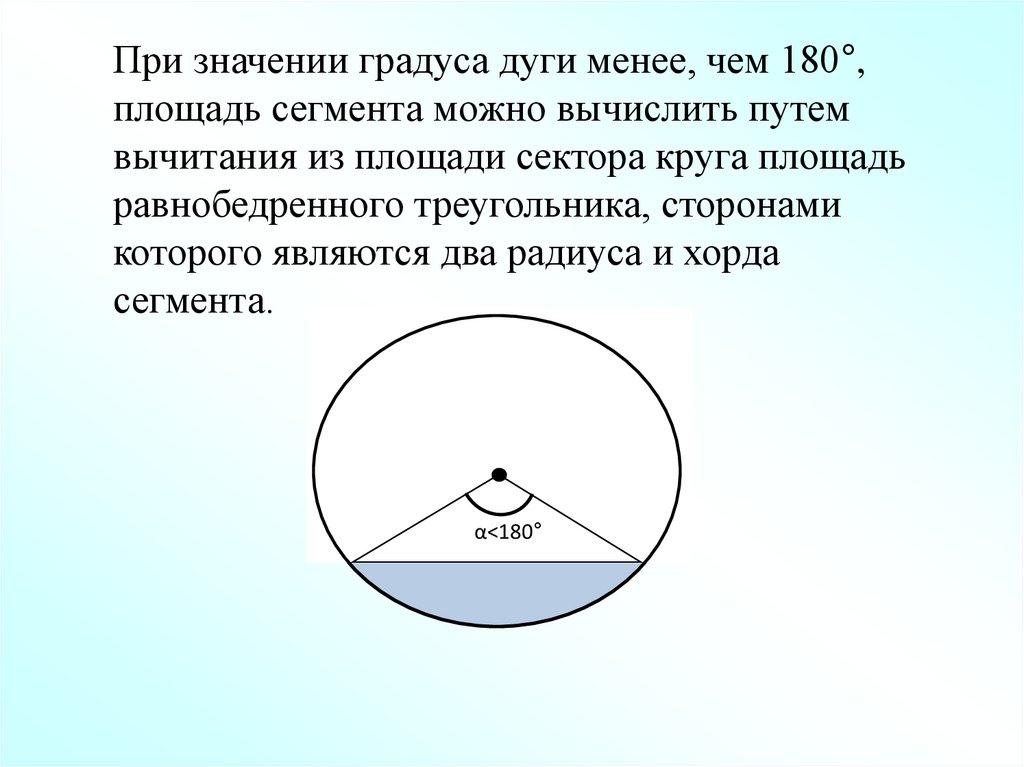
При значении градуса дуги менее, чем 180°,площадь сегмента можно вычислить путем
вычитания из площади сектора круга площадь
равнобедренного треугольника, сторонами
которого являются два радиуса и хорда
сегмента.
α<180°
10. Задание 1. Впишите пропущенное слово:
Кругом называется часть __________, ограниченнаяокружностью.
11. Задание 2. Питон длиной 7 м свернулся в круг. Найдите площадь образуемого им круга.
Задание 2. Питон длиной 7 мсвернулся в круг. Найдите площадь
образуемого им круга.
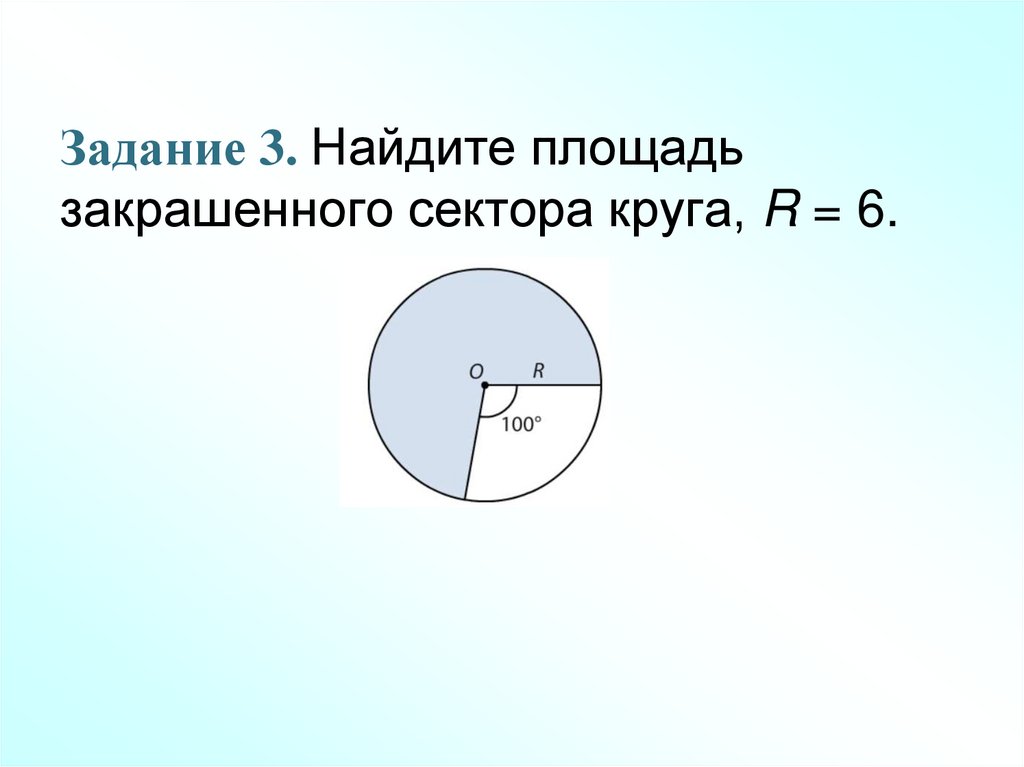
12. Задание 3. Найдите площадь закрашенного сектора круга, R = 6.
Задание 3. Найдите площадьзакрашенного сектора круга, R = 6.
13. Домашнее задание:
ДОМАШНЕЕ ЗАДАНИЕ:Выпишите и выучите формулы
Задание 1. Перепиши в тетрадь предложение, вставив в него
пропущенное слово.
Задание 2. Запиши краткое решение задачи.
Задание 3. Запиши краткое решение задачи.











 mathematics
mathematics








