Простейшие показательные неравенства

1.

02.03.23
Простейшие
показательные
неравенства

2.

Показательные
неравенства
Определение
Простейшие
неравенства
Решение неравенств

3.

Определение
Показательные неравенства –
это неравенства, в которых
неизвестное содержится в
показателе степени.
Примеры:
х
3 ≤ 9;
х
х+1
2 +5⋅ 2 >11

4.

Виды неравенств
Линейное нер-во
2х+7>0
-8х+4<0
Квадратное нер-
во
х^2-4х+3>0

5.

Простейшие
показательные
неравенства – это
неравенства вида:
x
b
x
b
a >a
x
b
a <a
a ≥a
x
b
a ≤a
где a > 0, a 1, b – любое число.

6.

При решении простейших
неравенств используют свойства
возрастания или убывания
показательной функции.
a > a |} ⇔x > b a > a | } ⇔ x < b
x
b
x
b

7.

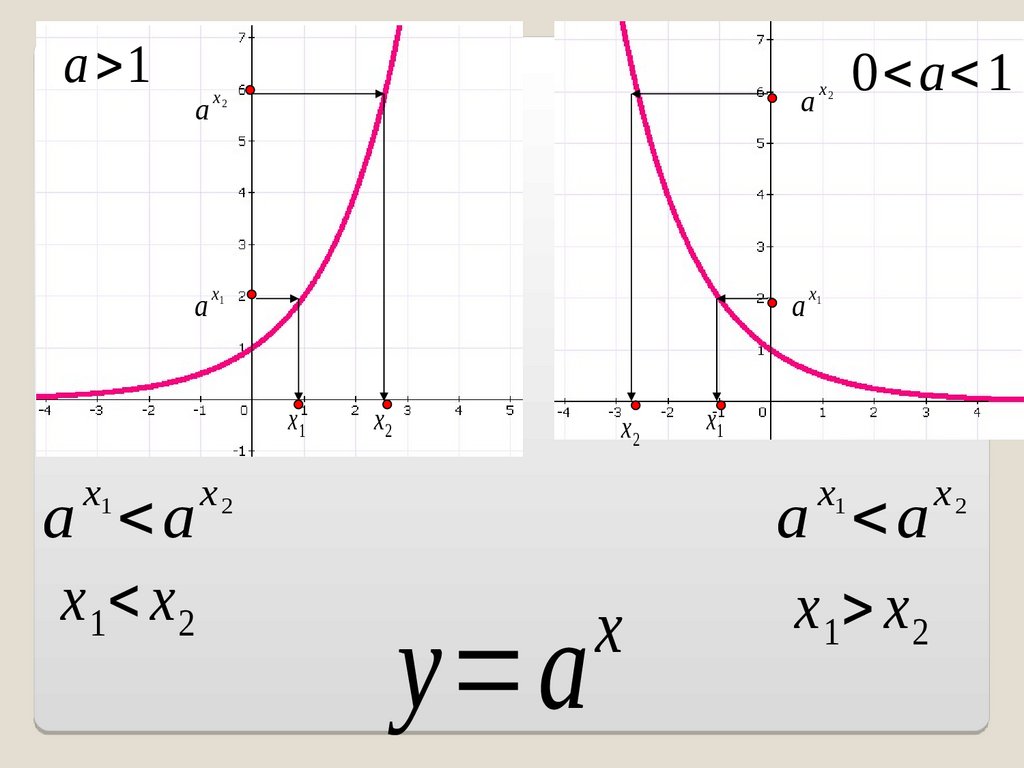
a >1
a
x2
a
x1
0<
a<
1
a
x2
a
x1
x1
a <a
x 1< x 2
x2
x2
x2
x1
x1
x1
y=a
x
a <a
x 1> x 2
x2

8.

Какие из перечисленных функций являются
возрастающими, а какие убывающими?
1¿ y=5
x
возрастающая , т. к .5>1
x убывающая ,т.к .0<0,5<1
2¿ y=0,5
x
возрастающая , т.к .10>1
3¿ y=10
x возрастающая , т. к . π >1
4¿ y=π

9.

Какие из функций являются
возрастающими, а какие убывающими?
()
2
5¿ y=
3
x
6¿ y=49
2
убывающая , т. к . 0< <1
3
−x
1
1
убывающая , т. к . 49 = и 0< <1
49
49
−1

10.

При а>1 функция возрастает
a
x
a
x
x0
a a a
x
x0
x a x0
x
x0
При 0<а<1 функция убывает
x
x
x
x
a
a x0 a
a
0
x
a a
x0
x0
0
x a
x0
x0

11.

Решения показательных
неравенств:
1. Способ Уравнивание оснований правой
и левой части

12.

Решите неравенство:
x
3 >81
x
4
3 >3
x
т . к. 3>1 , то функция y=3 возрастающая
x >4
x0

13.

Решите неравенство:
()()
x
1x
1
0 ≥
2
2
3
2
()
x
1
1
т .к.0< <1 ,то функция y=
убывающая
2
2
3
x≤
2
x∈¿

14.

Решите неравенство:
3x 1
2 ≥ ;
2
3x
−1
2 ≥2 ;
т . к. основание 2 >1 , тофункция возрастающая
3 x≥ −1;
1
x ≥− ;
3
x∈¿

15.

Показательные неравенства
Простейшие показательные неравенства
Неравенства, решаемые вынесением за
скобки степени с меньшим показателем
Неравенства, решаемые введение новой
переменной

16.

Простейшие
показательные неравенства
х
1¿. 3 >9 ⇔ 3 x > 32 ⇔ x >2
Ответ: х >2 .
2¿.
()
х
1 1
> ⇔
2 4
Ответ: х < 2 .
() ()
x
1
1
>
2
2
2
⇔ x <2

17.

Решение показательных неравенств
Способ 2: Вынесение за скобки степени с
меньшим показателем
х− 3 1
х
3 + ⋅ 3 >10
3
3
х− 3
3
3
1 3
(1+ ⋅ 3 )>10
3
х− 3
х− 3
(1+9)>10
⋅ 10>10 : 10
х− 3
>1
х− 3
0
3
3
3 > 1, то
>3
х − 3>0
х >3 .
Ответ: х >3

18.

Решение показательных неравенств
Способ 3: введение новой переменной
х
х
9 −10 ⋅ 3 <−9
2х
х
3 −10 ⋅ 3 +9 <0
х
3 =t (t>0)
(t − 9) ( t − 1) <0
1<t <9
2
t − 10 t+9< 0
D=102 − 4 ⋅ 9=100 −36=64=82
10+8 18
t 1=
= =9
2
2
10 −8 2
t 2=
= =1
2
2
x
1<3 < 9
х
0
3 <3 ; 3 >3 ;
х
2
х <2
3>1, то
х >0 .
Ответ: х < 2. х>0

19.

Показательные неравенства в ЕГЭ(профиль)
ТИП 14 Решите неравенство:
1)
11)
21)
31)
2)
12)
22)
32)
3)
13)
23)
33)
4)
14)
24)
34)
5)
15)
25)
35)
6)
16)
26)
36)
7)
17)
27)
37)
8)
18)
28)
38)
9)
19)
29)
39)
10)
20)
30)
40)

20.

Показательные неравенства в ЕГЭ(база)
ТИП 17 Найдите корень уравнения
1)
8)
2)
9)
3)
4)
5)
6)
7)

21.

Домашняя работа
п.6.4 изучить стр.173 (учебник 10 класс)
Выполнить задания ЕГЭ на решение
простейших логарифмических уравнений
тип 5 (профиль (13 прототипов)) или тип
17(база (9 прототипов))