Показательные неравенства

1.

2.

;
1. Область определения функции
0;
С в о й с т в а показательной функции
2. Область значений функции
у ах , а 1
3. Промежутки сравнения значений
функции с единицей
при x 0, a x 1
при x 0, 0 a x 1
4. Четность, нечетность
у ах , 0 a 1
при x 0, 0 a x 1
при x 0, a x 1
Функция не является ни чётной, ни
нечётной (функция общего вида).
5. Монотонность
монотонно
возрастает на R
6. Экстремумы
Показательная функция экстремумов
не имеет
7. Асимптота
8. При любых действительных значениях х
и у; a>0, a≠1; b>0, b≠1.
монотонно
убывает на R
Ось Ох является горизонтальной
асимптотой
1) а х а у а х у ;
2) a x :а у а х у ;
3) аb а хb х ;
х
х
ах
а
4) х ;
b
b
5) а х
у
а ху ;
6) r Q и a b, то
аr br при r 0
аr br при r 0;
7) r, s Q и r s, то
аr as при а 1
аr as при 0 а 1.

3.

ОПРЕДЕЛЕНИЕ
простейших показательных неравенств:
Пусть а – данное положительное, не
равное единице число и b – данное
действительное число. Тогда неравенства
ax > b (ax ≥ b) и ax < b (ax ≤ b)
называются простейшими
показательными неравенствами.

4.

ЧТО НАЗЫВАЕТСЯ
решением неравенства?
Решением неравенства с
неизвестным х называют число х0, при
подстановке которого в неравенство
получается верное числовое
неравенство.

5.

ЧТО ЗНАЧИТ
решить неравенство?
Решить неравенство –
значит, найти все его решения или
показать, что их нет.

6.

Рассмотрим взаимное расположение графика
функции y=ax, a>0, a≠1 и прямой y=b
y ax , a 1 и b R
y ax , 0 a 1 и b R
y
y
y=b, b>0
y=b, b>0
1
y=b, b=0
y=b, b<0
0
1
х0
x
х0
0
y=b, b=0 x
y=b, b<0

7.

ВЫВОД №1:
При b ≤ 0 прямая y=b не пересекает
график функции y=ax, т.к. расположена
ниже кривой y=ax, поэтому неравенства
ax > b (ax ≥ b) выполняются при x R, а
неравенства ax < b (ax ≤ b) не имеют
решения.
2х 5 справедливо при любых х
2x 0 и 5 0
x
1
4 справедливо при любых х
3
1
0 и 4 0
3
10x 3 решений нет
10x 0 и 3 0
x
x
1
10 решений нет
7
x
1
0 и 10 0
7

8.

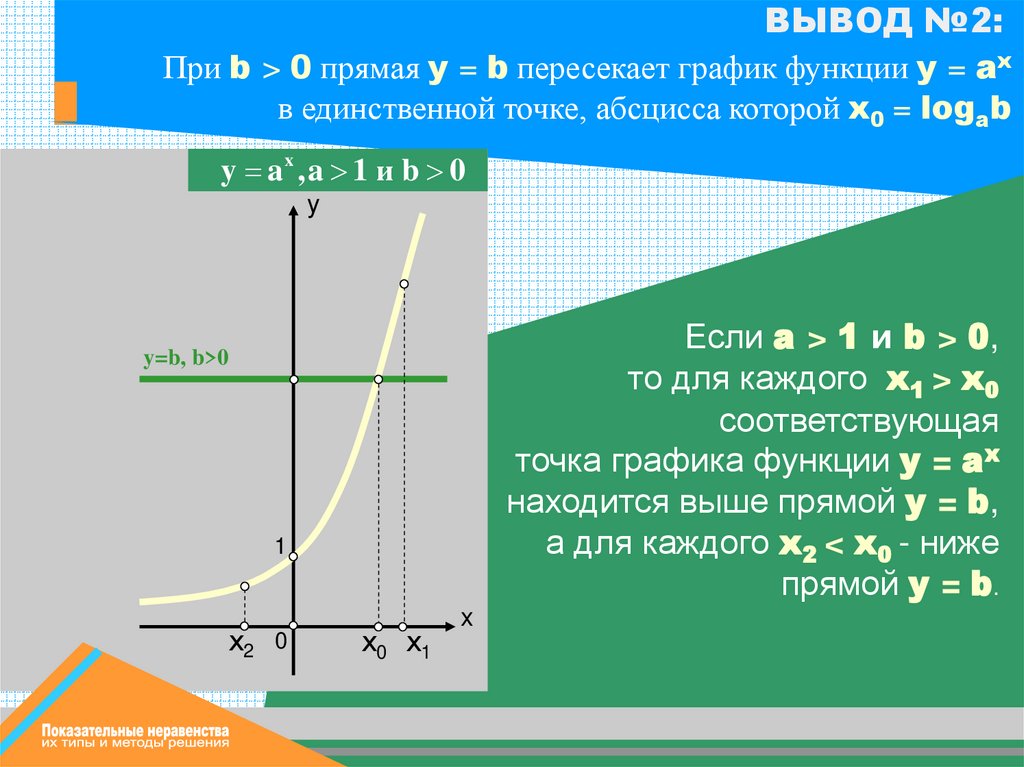
ВЫВОД №2:
При b > 0 прямая у = b пересекает график функции y = ax
в единственной точке, абсцисса которой x0 = logab
y ax , a 1 и b 0
y
Если a > 1 и b > 0,
то для каждого x1 > x0
соответствующая
точка графика функции y = ax
находится выше прямой y = b,
а для каждого x2 < x0 - ниже
прямой y = b.
y=b, b>0
1
х2
0
х0 х1
x

9.

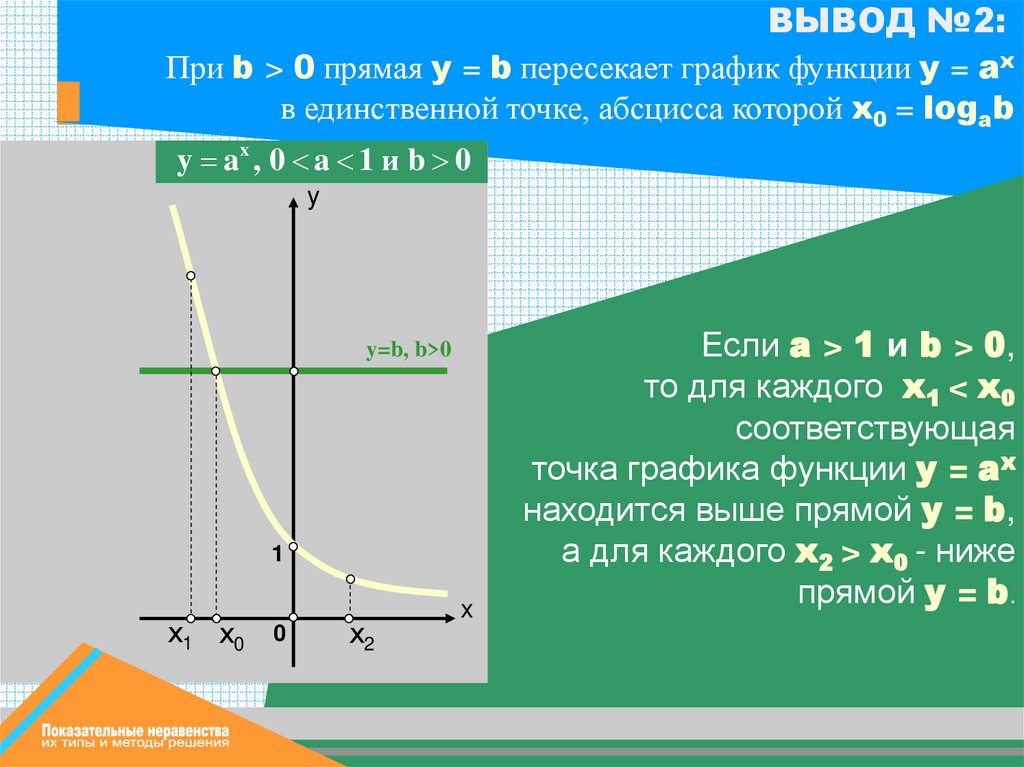
ВЫВОД №2:
При b > 0 прямая у = b пересекает график функции y = ax
в единственной точке, абсцисса которой x0 = logab
y ax , 0 a 1 и b 0
y
y=b, b>0
1
х1 х0
0
х2
x
Если a > 1 и b > 0,
то для каждого x1 < x0
соответствующая
точка графика функции y = ax
находится выше прямой y = b,
а для каждого x2 > x0 - ниже
прямой y = b.

10.

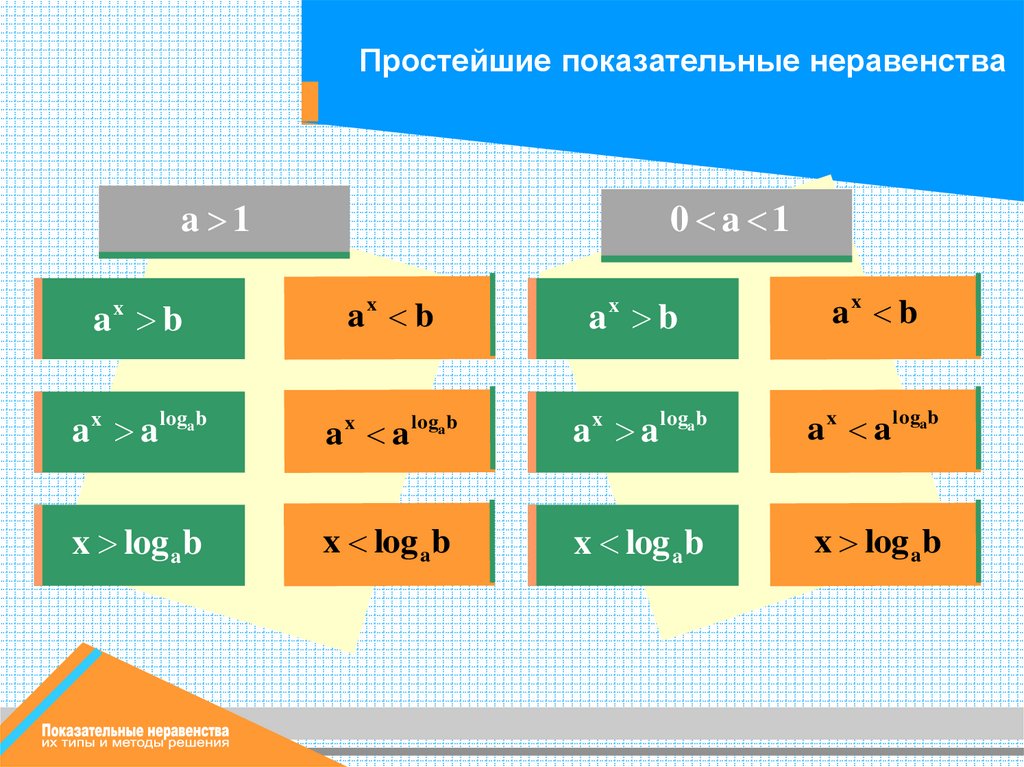
Простейшие показательные неравенства
a 1
a b
x
0 a 1
ax b
a x a logab
a a
x log ab
x log ab
x
loga b
ax b
ax b
a x a logab
a x a logab
x log ab
x log ab