Показательные неравенства и уравнения

1.

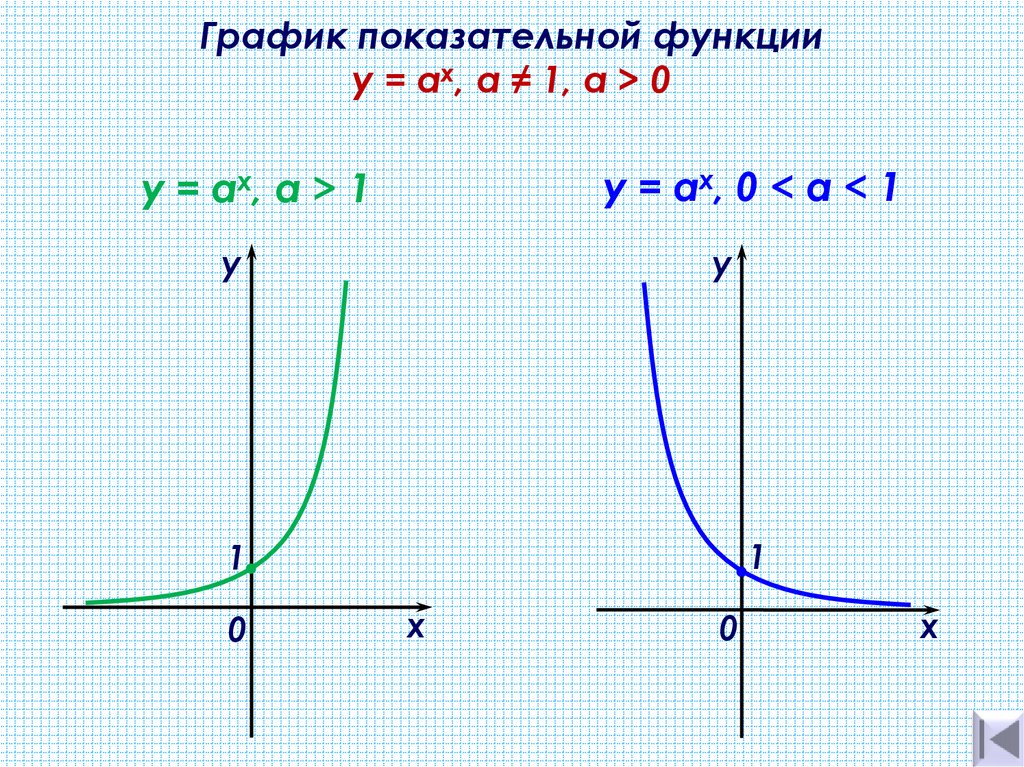
График показательной функции
y = ах, а ≠ 1, a > 0
y = ах, 0 < а < 1
y = ах, а > 1
у
у
1
1
0
х
0
х

2.

Показательные уравнения
Уравнения вида af(x) = аh(х), где а ≠ 1, a > 0
называют показательными уравнениями
⟺
af(x) = аh(х)
f(x) = h(х)
Методы решения показательных уравнений:
1. Функционально-графический метод.
2. Метод уравнивания показателей.
3. Метод введения новой переменной.

3.

Показательные уравнения. Примеры
Пример 1
2x 4
2
64
22x 4 26
2x 4 6
x 5
Ответ : 5
Пример 2
1
3
2 x 3,5
Пример 3
5
1
3
2 x 3,5
1
1
3
3
2x 3,5 0,5
x 2
Ответ : 2
x 2 3 x
5 3 x 8
x 2 3 x 3x 8
0,5
x 2 6x 8 0
x1 2,
x 4
2
Ответ : 2; 4

4.

Показательные уравнения. Примеры
Пример 4
4x 2х 1 24 0
2
2
2 х
2 2х 24 0
х 2
2 2х 24 0
Пусть 2х t , где t 0 тогда
t 2 2t 24 0
t1 6,
t 4
2
t1 6 не уд ет условию t 0
Вернемся к исходной переменной
2х 4
х 2
Ответ : 2

5.

Показательные уравнения. Примеры
Пример 5 (однородное уравнение)
52x 1 13 15 х 54 9 х 1 0
5 5
2x
5 52x
9х
13 15 54
0
9
13 15 х 6 9 х 0
х
Разделим на 9 х , тогда
5 5
9х
2x
5
5
3
2х
13 15
6 9
0
х
х
9
9
х
х
х
5
13 6 0
3
5t 2 13t 6 0
3
t1 5 ,
t 2 2
Вернемся к исходной переменной
х
х
3
5
5
3
х 1
или
5
2
3
х log 5 2
3
х
5
Пусть t , где t 0, тогда
3
Ответ : 1; log 5 2.
3

6.

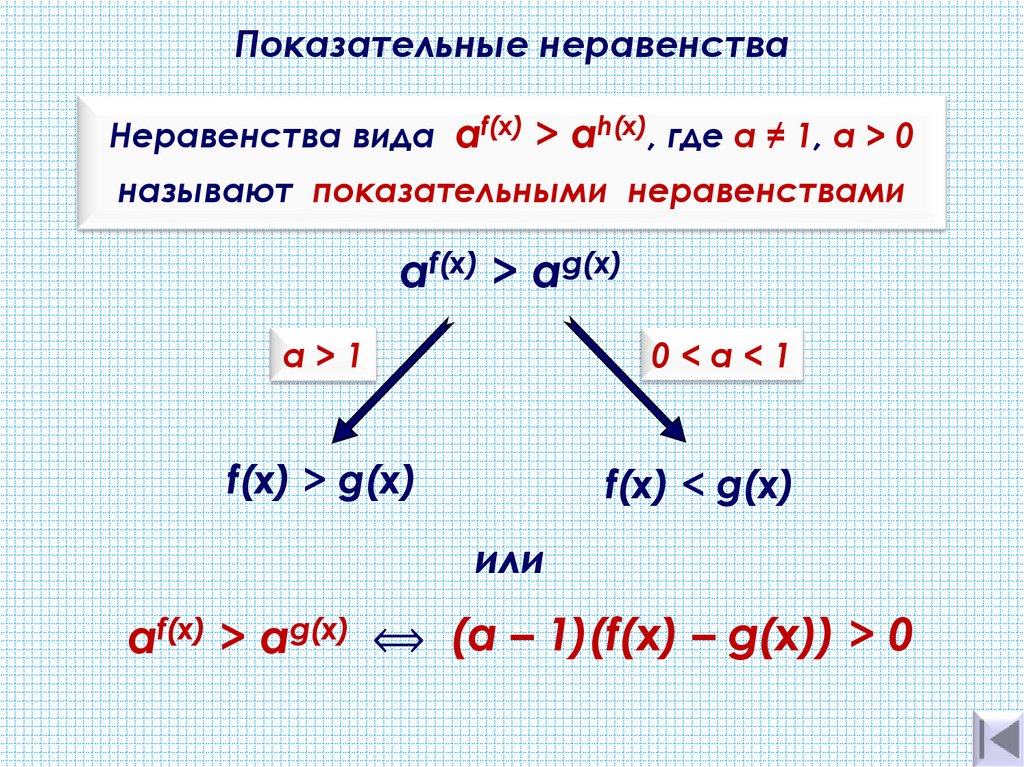
Показательные неравенства
Неравенства вида af(x) > аh(х), где а ≠ 1, a > 0
называют показательными неравенствами
af(x) > аg(х)
а>1
0<а<1
f(x) > g(х)
f(x) < g(х)
или
af(x) > аg(х) ⟺ (а – 1)(f(x) – g(x)) > 0

7.

Показательные неравенства. Примеры
Пример 1
22 x 4 64
22 x 4 26
т.к . функция у 2t монотонно
возрастает на R , то
2x 4 6
x 5
Ответ : 5;
Пример 2
1
3
2 x 3 ,5
1
3
2 x 3 ,5
1
3
1
3
0 ,5
t
1
т.к . функция у
3
монотонно убывает на R , то
2x 3 ,5 0 ,5
x 2
Ответ : 2;

8.

Показательные неравенства. Примеры
Пример 4
8 x 18 х 2 27 x
23 x 2х 32x 2 33 x
: 33 х , т.к . 33 х 0
23 x 2х 32x 2 33 x
3х
3х
3
3
33 х
2
3
3x
x
2
2
3
x
2
Пусть t , где t 0
3
t3 t 2 0
t 3 t 2 t 3 t 1 1 t 3 1 t 1 t 1 t 2 t 2
т.к . t 2 t 2 0 для любых t , то t 1 0
t 1

9.

Показательные неравенства. Примеры
Пример 4
Вернемся к исходной переменной :
x
2
1
3
x
0
2
2
,
3
3
x
т.к . а
2
2
1, то ф ция у убывает на R
3
3
x 0
Ответ : ; 0 .