Логарифмические неравенства

1.

2.

кросс–опрос
Концентрация внимания:
Вклад каждого
учёного в развитие
логарифмов
Ответ
Непер
Изобрёл логарифмы, их название, создал первые таблицы
логарифмов
Бюрги
Создатель таблиц логарифмов параллельно с Непером
Эйлер
Ввёл обозначение числа е и вычислил его с точностью до
23 знаков
Бриггс
Составил таблицы десятичных логарифмов
Оутред
Изобретатель логарифмической линейки
Ламберт
Эрмит
Менголи
Доказал иррациональность числа е (т. е. число е не может быть
квадратом какого-либо числа)
Доказал трансцендентность числа е (т.е. число е не может быть
корнем какого-либо алгебраического уравнения)
Ввёл термин «натуральные логарифмы»
Концентрация внимания равна N.
N = (число верных ответов) х 0,125 х 100%.

3.

С в о й с т в а логарифмической функции
Свойства функции
1. Область определения
2. Область значений
3. Четность, нечетность
4. Нули функции
5. Промежутки
знакопостоянства
6. Экстремумы
7. Промежутки монотонности
при x 0;
8. Асимптота
a 1
0 a 1
0;
;
Функция не является ни четной, ни нечетной
y 0 при x 1
y 0 при х 1;
y 0 при x 0;1
y 0 при х 0;1
y 0 при x 1;
Функция экстремумов не имеет
Функция возрастает
Функция убывает
x 0

4.

Рассмотрим взаимное расположение графика
функции y=logax (a>0, a≠1) и прямой y=b
y=logax (a>1)
y
y=logax (0<a<1)
y
0 х01
y=b, b>0
х0
y=b, b>0
y=b, b=0
х0
x
y=b, b<0
х0
0
y=b, b=0
1
х0
y=b, b<0 x

5.

ВЫВОД:
График функции y=logax (a>0, a≠1) и
прямая y=b пересекаются в единственной
точке, абсцисса которой x0=ab.

6.

ОПРЕДЕЛЕНИЕ:
Пусть a 0, a 1, b R , тогда
неравенства logax > b (logax ≥ b) или
logax < b (logax ≤ b) называются
простейшими
логарифмическими
неравенствами.

7.

Что значит решить неравенство?
Решить неравенство - значит,
найти все его решения или показать,
что их нет.

8.

Что называется решением неравенства?
Решением неравенства
с неизвестным х называют число х0, при
подстановке которого в неравенство вместо х
получается верное числовое неравенство.

9.

ВЫВОД №1:
y=logax (a>1)
y
y=b
х1
0
1
х0
х2
x
Если a 1
для каждого x 2 x 0
соответствующая точка
графика функции y log a x
находится выше прямой
y b
для каждого 0 x 1 x 0
соответствующая точка
графика функции y log a x
находится ниже прямой
y b

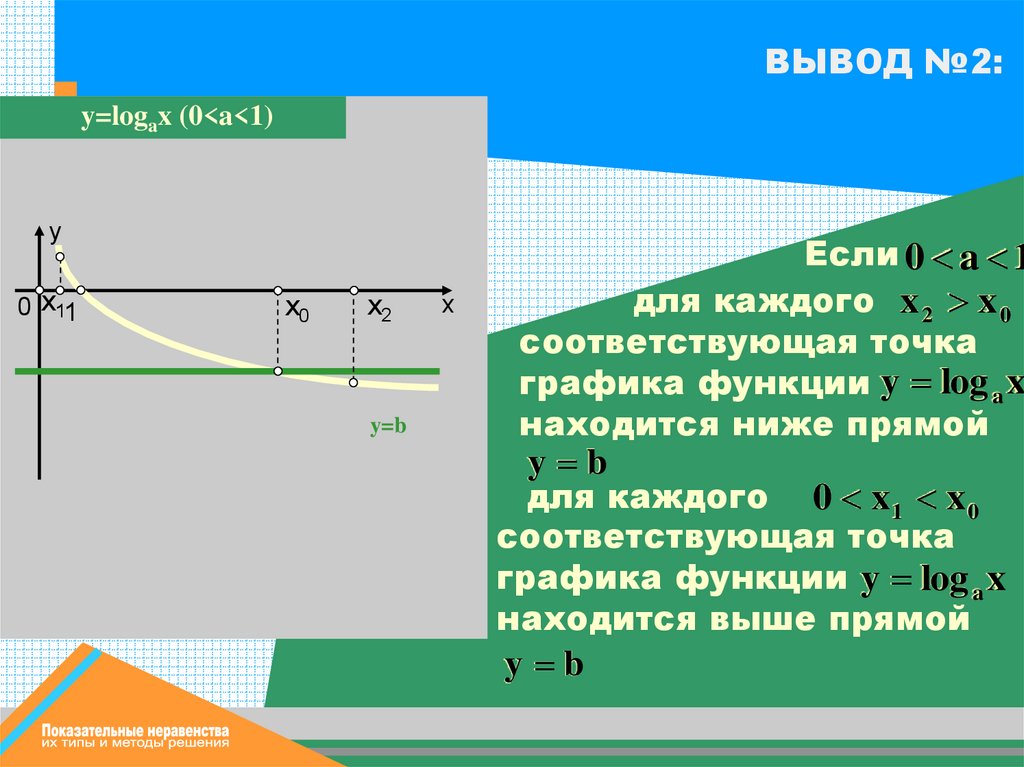
10.

ВЫВОД №2:
y=logax (0<a<1)
y
0 х11
х0
х2
y=b
x
Если 0 a 1
для каждого x 2 x 0
соответствующая точка
графика функции y log a x
находится ниже прямой
y b
для каждого 0 x 1 x 0
соответствующая точка
графика функции y log a x
находится выше прямой
y b

11.

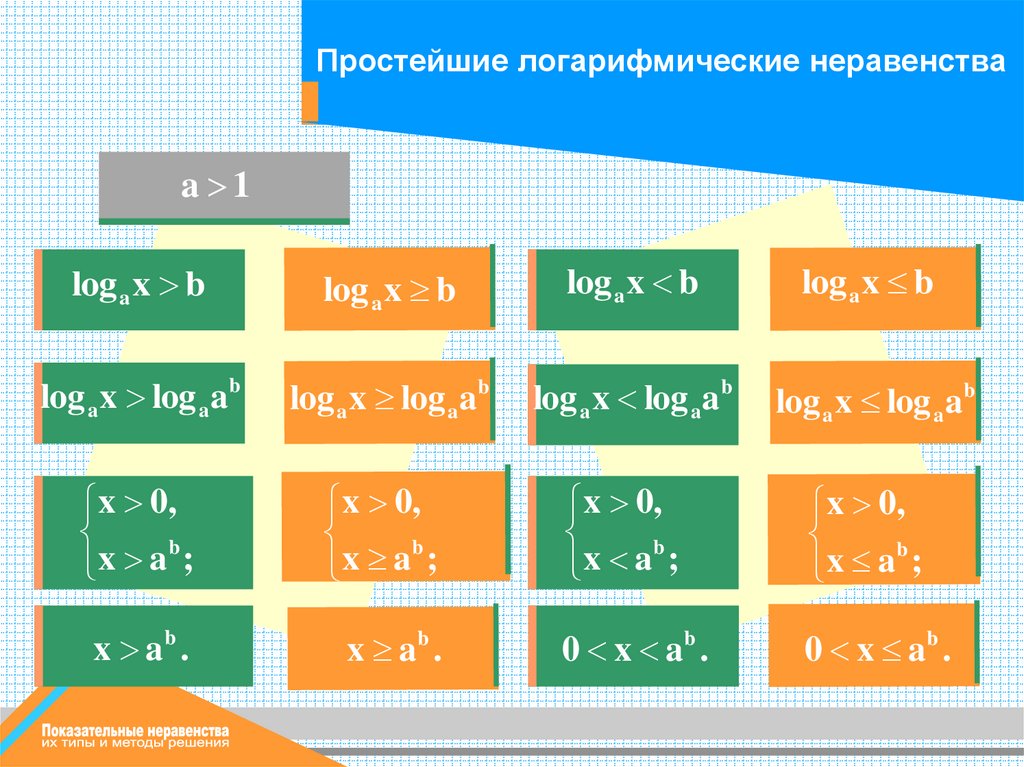
Простейшие логарифмические неравенства
a 1
log a x b
log a x b
log a x b
log a x b
log a x log aab
log a x log aab
log a x log aab
log a x log aab
x 0,
b
x
a
;
x 0,
b
x
a
;
x 0,
b
x
a
;
x 0,
b
x
a
;
x ab .
x ab .
0 x ab .
0 x ab .

12.

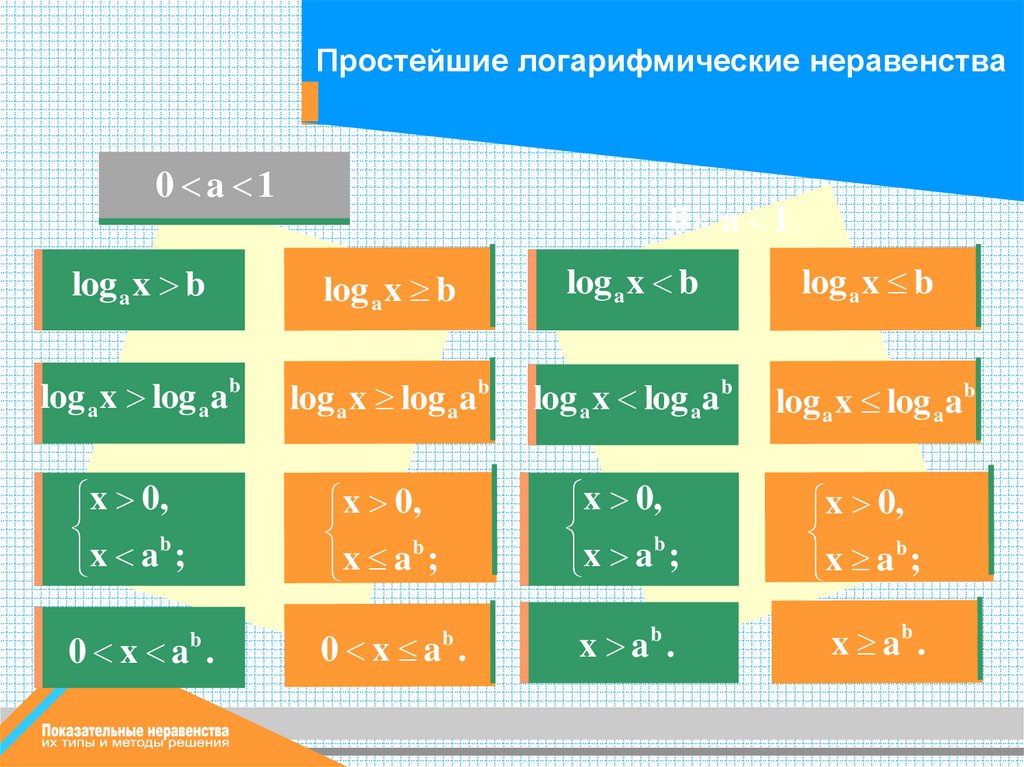
Простейшие логарифмические неравенства
0 a 1
0 a 1
log a x b
log a x b
log a x b
log a x b
log a x log aab
log a x log aab
log a x log aab
log a x log aab
x 0,
b
x
a
;
x 0,
b
x
a
;
x 0,
b
x
a
;
x ab .
x ab .
x 0,
b
x
a
;
0 x a .
b
0 x a .
b

13.

Типы и методы решения логарифмических неравенств
1) Простейшие логарифмические неравенства
Пример №1
log 1 (5x 1) 0
Решение:
3
Т.к. D(log a ) 0; , a 0 , a 1;
1
y log 1 t 0 1 убывает на всей
3
3
области определения и log 1 1 0, то неравенство равносильно системе
3
5x 1 0,
5x 1 1;
x 0,2 ,
x 0,4;
0,2 x 0,4.
Ответ:
(0,2; 0,4)

14.

Типы и методы решения логарифмических неравенств
1) Простейшие логарифмические неравенства
Пример №2
log 0,5 (4x 3) log 0,5 (x 3)
Решение:
Т.к. D(log a ) 0; , a 0 , a 1; y log 0,5 t (0 0,5 1) убывает
на всей области определения, то неравенство равносильно системе
4x 3 x 3,
4x 3 0;
x 2,
x 0,75;
0,75 x 2.
Ответ:
(0,75; 2)

15.

Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим
логарифмическим неравенствам
Решение:
Пример №1
log 5 (3x 1) log 1 (1 x 2 ) 0,
log 5 (3x 1) log 1 (1 x 2 ) 0
5
5
log 5 (3x 1) log 5 (1 x 2 ) 0,
log 5 (3x 1) log 5 (1 x 2 ).
Т.к. D(log a ) 0; , a 0 , a 1 и y log 5t (5 1)
возрастает на всей области
определения, то неравенство равносильно системе
3x 1 1 x 2 ,
1 x 2 0;
3x 1 1 x 2 .
т.к. 1 x 2 0, при x R, то система равносильна неравенству
x 2 3x 2 0,
1 x 2.
Ответ:
1; 2

16.

Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим
логарифмическим неравенствам
Решение:
Пример №2
log 3 x log 3 x log 1 x 6
log 3 x log 3 x log 1 x 6,
3
3
log 3 x 2log 3 x log 3 x 6,
2log 3 x 6,
log 3 x 3.
Т.к. D(log a ) 0; , a 0 , a 1; y log 3t (3 1) возрастает на всей
области определения и
x 0,
x 27;
3 log 3 27, то неравенство равносильно системе
0 x 27.
Ответ:
0;27

17.

Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим
логарифмическим неравенствам
Решение:
Пример №3
log 0,5 (x 0,5) log 0,5 (x 1) 1
log 0,5 (x 0,5) log 0,5 (x 1) 1.
Т.к. D(log a ) 0; , a 0 , a 1;
y log 0,5 t (0 0,5 1) убывает на всей области определения и log 0,5 0,5 1,
то неравенство равносильно системе
x 0,5 0,
x 1 0,
log 0,5 (x 0,5) log 0,5 (x 1) 1;
x 1,
2
x - 1,5x 0;
x 0,5,
x 1,
x 1,
(x 0,5)(x 1) 0,5;
log 0,5 (x 0,5)(x 1) 1;
x 1,
0 x 1,5;
1 x 1,5.
Ответ:
1; 1,5

18.

Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим
логарифмическим неравенствам
Решение:
Пример №4
1 log 5 (x 3) log 5 (x 1)
1 log 5 (x 3) log 5 (x 1).
Т.к. D(log a ) 0; , a 0 , a 1; y log 5t (5 1)
возрастает на всей области определения и 1 log 5 5, то неравенство равносильно системе
x 3 0,
x 1 0,
1 log 5 (x 3) log 5 (x 1);
x 3,
(x 1)(x 3) 5;
x 3,
x 1,
log 5 (x 1) log 5 (x 3) 1;
x 3,
log (x 1)(x 3) 1;
5
x 3,
x 2 2x 8 0;
x 3,
x 2,
x 4;
x 3,
x 2,
x 3,
x 4;
x 4.
Ответ:
4;

19.

Типы и методы решения логарифмических неравенств
3) Логарифмические неравенства, сводящиеся к
неравенствам второй степени
Решение:
Пример №1
2log 21 x 5log 1 x 2 0
2log 21 x 5log 1 x 2 0.
2
2
2
Пусть log 1 x t, тогда 2t 2 5t 2 0,
2
Вернёмся к переменной х
x 0,
log x 0,5 ,
0,5
log 0,5 x 2;
2
t 0,5 ,
t 2.
Т.к. D(log a ) 0; , a 0 , a 1, то
x 0,
log 2 x 0,5 ,
log 2 x 2;
x 0,
log 2 x 0,5 ,
log 2 x 2;
y log 2r (2 1) возрастает на всей области определения, то
x 0,
x 0,
1
1
0
x
,
x
,
1
,
x
4
4
x 0,
1
2
x
.
1
1
2
x
;
x
;
4
2
Ответ:
1 1
;
0;
4 2

20.

Типы и методы решения логарифмических неравенств
3) Логарифмические неравенства, сводящиеся к
неравенствам второй степени
Решение:
3
log 3 log 3 (3x) 4log 3 x 4. Т.к. D(log a ) 0; , a 0 , a 1,
x
то для нахождения области допустимых значений
переменной х составим систему:
Пример №2
3
log 3 log 3 (3x) 4log 3 x 4
x
3
В найденной области допустимых значений переменной х преобразуем
x 0,
неравенство.
log 3 3 log 3 x log 3 3 log 3x 4 1 log 3 x ,
3x 0, x 0.
x 0;
1 log 3x 1 log 3x 4 1 log 3x 0,
1 log 3 x log 3x 3 0,
log 3 x 1,
log 3x 1 log 3x 3 0,
log 3 x 3; y log 3t (3 1)
возрастает на всей области определения и 1 log 3 3, а также 3 log 3 27.
x 3,
С учётом области допустимых значений переменной х получим:
x 27.
x 0,
x 0,
x 3,
0 x 3,
x 3,
x 0,
x 27.
x 27;
x 27;
Ответ:
(0;3) (27; )

21.

Типы и методы решения логарифмических неравенств
4) Логарифмические неравенства, сводящиеся к
рациональным неравенствам
Решение:
Пример №1
2
1
0
lgx lg0,1 lgx
Пусть lgx t и lg0,1 1, тогда
2
1
0,
t 1 t
t 1
0,
t(t 1)
Вернёмся к переменной х
x 0,
1 lgx 0,
lgx 1;
1 t 0,
t 1.
x 0,
0,1 x 1,
x 10;
Т.к. D(log a ) 0; , a 0 , a 1, то
x 0,
y lgr (10 1)
lg0,1 lgx lg1,
lgx lg10;
возрастает на всей
области определения
x 0,
0,1 x 1,
x 0,
x 10;
0,1 x 1,
x 10.
Ответ:
0;1 10;

22.

Типы и методы решения логарифмических неравенств
4) Логарифмические неравенства, сводящиеся к
рациональным неравенствам
Решение:
Пример №2
Т.к. D(log a ) 0; , a 0 , a 1, то x 0,
x 1.
В найденной области допустимых
значений переменной х преобразуем
данное неравенство к виду:
1
5
log 3 x
.
log 3 x 2
1 5
Пусть log 3 x t. Тогда t ,
t 2
2t 2 5t 2
0,
2t
t 2 t 1
2 0,
t
x 0 , x 1,
1 x 3 ,
x 9;
log 1 x log x 3
3
5
2
Вернёмся к переменной х.
1
0
t
,
2
t 2.
1 x 3 ,
x 9.
x 0, x 1,
1
0
log
x
,
3
log x 2; 2
3
y log 3r (3 1)
возрастает на
всей области определения и
1
log 3 3 ,
2
Ответ:
2 log 3 9
1; 3 9;

23.

Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и
под знаком логарифма
Решение:
Пример №1
log 1 3x 3 0
log 1 3x 3 0.
Т.к. log 1 3x 3 0 и 3 1, то
0 1 3x 1,
1 3x 0,
1
0 x .
3
Ответ:
1
0;
3

24.

Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и
под знаком логарифма
Решение:
Пример №2
log x (2x 5) 1
log x (2x 5) 1,
log x (2x 5) log x x.
Т.к. D(log a ) 0; , a 0 , a 1, то
2x 5 0,
0 x 1,
2x 5 x,
x 1
2x 5 x;
x 2,5 ,
0 x 1,
x 5,
x 1,
x 5;
x 2,5 ,
x 1;
x 1.
Ответ:
1;

25.

Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и
под знаком логарифма
Решение:
Пример №3
log x (2x 3) 2
log x (2x 3) 2,
log x (2x 3) log x x 2 .
Т.к. D(log a ) 0; , a 0 , a 1, то
2x 3 0 ,
0 x 1,
2
2x
3
x
,
x 1,
2x 3 x 2 ;
x 1,5 ,
0 x 1,
2
x 2x 3 0,
x 1,
x 2 2x 3 0;
x 1,5 ,
0 x 1,
1 x 3,
x 1,
x 1,
x 3;
x 1,5 ,
0 x 1, 0 x 1 ,
x 3.
x 3;
Ответ:
(0;1) 3;