Similar presentations:
Логарифмические уравнения
1.
2.
Концентрация внимания:кросс–опрос
Вопрос
Ответ
Сформулируйте определение
логарифма
log a b x a x b , a 0 , a 1, b 0
Чему равен логарифм произведения?
log a xy log a x log a y, a 0 , a 1, x 0, y 0
Чему равен логарифм частного?
log a
Чему равен логарифм степени числа?
log a x p plog a x, a 0 , a 1, x 0 , p R
Чему равен логарифм степени основания?
log a q x
Чему равен логарифм степени числа и
основания?
log a q x p
Запишите формулу перехода к логарифму
другого основания
log a b
log c b
a 0, a 1, c 0, c 1, b 0
log c a
Запишите частный случай формулы
перехода к логарифму другого основания
log a b
1
a 0, a 1, b 0, b 1
log b a
x
log a x log a y , a 0 , a 1, x 0 , y 0
y
1
log a x , a 0, a 1, x 0, q 0, q R
q
p
log a x, a 0, a 1, x 0, q 0, q; p R
q
Концентрация внимания равна N.
N = (число верных ответов) х 0,125 х 100%.
3.
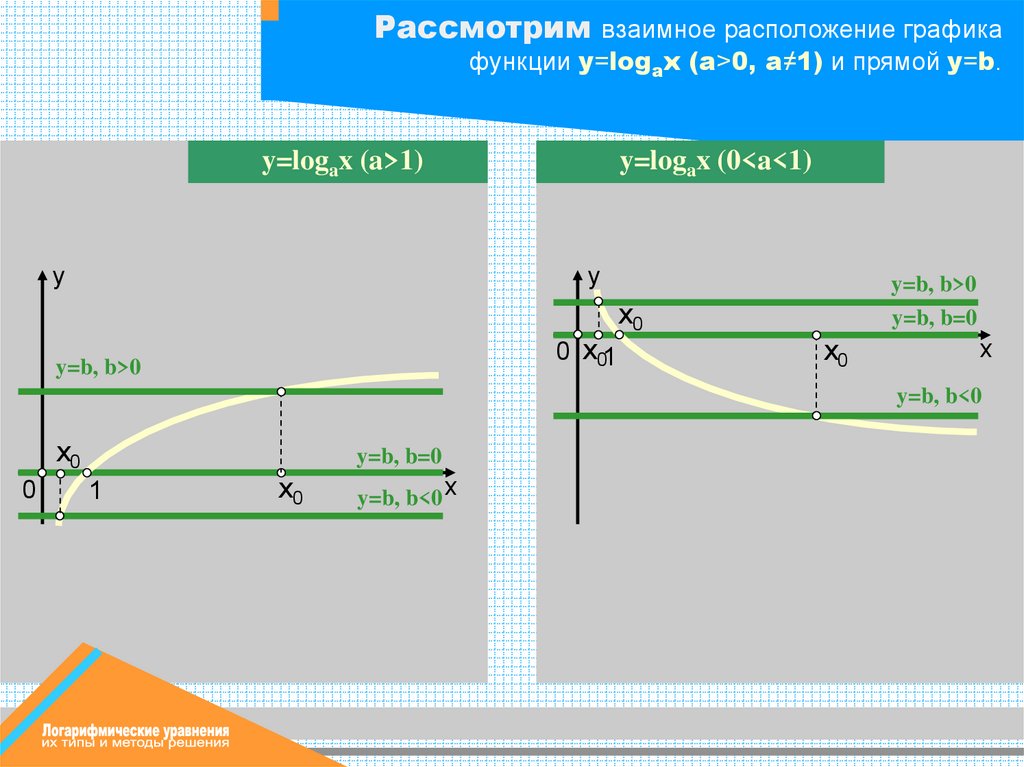
Рассмотрим взаимное расположение графикафункции y=logax (a>0, a≠1) и прямой y=b.
y=logax (a>1)
y
y=logax (0<a<1)
y
0 х01
y=b, b>0
х0
y=b, b>0
y=b, b=0
х0
x
y=b, b<0
х0
0
y=b, b=0
1
х0
y=b, b<0 x
4.
ВЫВОД:График функции y=logax (a>0, a≠1) и
прямая y=b пересекаются в единственной
точке, т.е. уравнение logax=b, a>0, a≠1,
x>0 имеет единственное решение x0=ab.
5.
ОПРЕДЕЛЕНИЕ:Уравнение logax=b, a>0, a≠1, x>0
называется простейшим
логарифмическим уравнением.
Пример:
log 3 x 2;
log 0,5 (2x 1) 1;
log 2x (x 2 3x 4) 2.
6.
Типы и методы решения логарифмических уравнений.ОПРЕДЕЛЕНИЕ:
Логарифмическими называются
уравнения, содержащие неизвестную
под знаком логарифма или в основании
логарифма (или и то и другое
одновременно).
7.
Типы и методы решения логарифмических уравнений.ДОПОЛНЕНИЕ:
При решении
логарифмических уравнений
необходимо учитывать:
область допустимых значений логарифма: под знаком
логарифма могут находиться только положительные величины;
в основании логарифмов - только положительные величины,
отличные от единицы;
свойства логарифмов;
действие потенцирования.
8.
Типы и методы решения логарифмических уравнений.1) Простейшие логарифмические уравнения.
Пример №1
log 2 (3x 2) 3
Решение:
log 2 (3x 2) 3.
Т.к.
D(log a ) 0; , a 0 , a 1 и 3 log 2 8, то
3x 2 0,
3x 2 8;
2
x
,
3
x 3 1 ;
3
1
x 3 .
3
Ответ:
1
3 .
3
9.
Типы и методы решения логарифмических уравнений.2) Логарифмические уравнения, сводящиеся к простейшим
логарифмическим уравнениям.
Решение:
Пример №1
log 16x log 4 x log 2 x 7,
log 16x log 4 x log 2 x 7
log 24 x log 22 x log 2 x 7,
1
1
log 2 x log 2 x log 2 x 7,
4
2
7
log 2 x 7,
4
log 2 x 4. Т.к. D(log a ) 0; , a 0 , a 1, то
x 0,
4
x
2
;
x 0,
x 16;
x 16.
Ответ:
16.
10.
Типы и методы решения логарифмических уравнений.2) Логарифмические уравнения, сводящиеся к простейшим
логарифмическим уравнениям.
Решение:
log
Т.к.
2
Пример №2
4 3x log 2 2 x 0,
log
D(log a ) 0; , a 0 , a 1, то
4 3x 0,
2 x 0,
log 4 3x log
2
2
2 x 0;
1
x
1
,
3
3x 2 10x 7 0;
2
4 3x log 2 2 x 0
3x 4,
x 2,
log 4 3x 2 x 0;
2
1
x
1
,
3
x 2 1 ,
3
x 1;
1
x 1 3 ,
x 1,
x 1 1 ,
3
1
x 2 ;
3
1
x
1
,
3
x 2,
4 3x 2 x 1;
x 1.
Ответ:
1.
11.
Типы и методы решения логарифмических уравнений.2) Логарифмические уравнения, сводящиеся к простейшим
логарифмическим уравнениям.
Решение:
Пример №3
log 3 x 2 log 3 5x 1 1,
log 3 x 2 log 3 5x 1 1
log 3 x 2 1 log 3 5x 1 ,
log 3 x 2 log 3 3 log 3 5x 1 ,
log 3 x 2 log 3 3 5x 1 .
Т.к.
D(log a ) 0; , a 0 , a 1, то
x 2 0,
x 2 3 5x 1 ;
x 2,
x 0,3125;
x 0,3125.
Ответ:
0,3125
12.
Типы и методы решения логарифмических уравнений.2) Логарифмические уравнения, сводящиеся к простейшим
логарифмическим уравнениям.
Решение:
lg 3x 1 lg 6x 3 0.
D(log a ) 0; , a 0 , a 1, то
3x 1 0,
3x 1,
6x
3
0,
6x 3,
lg 3x 1 lg 6x 3 0; lg 3x 1 0,
lg 6x 3 0;
1
x
,
2
2
x .
3
x 2
3;
Т.к.
Пример №4
lg 3x 1 lg 6x 3 0
1
x ,
3
1
x ,
2
3x 1 1,
6x 3 1;
1
x
,
2
2
x ,
3
2
x 3 ;
Ответ:
2
3
13.
Типы и методы решения логарифмических уравнений.3) Логарифмические уравнения, сводящиеся к квадратным
уравнениям.
Решение:
Пример №1
2log 22 x 5log 2 x 3 0
2log 22 x 5log 2 x 3 0.
t 3,
2
1
Пусть log 2 x t, тогда 2t 5t 3 0 и
t
.
2
Вернемся к переменной х.
Т.к.
D(log a ) 0; , a 0 , a 1, то
x 0,
log 2 x 3,
1
log
x
;
2
2
x 0,
x 8,
1
x
;
2
x 0,
x 8,
x 0,
1
x
;
2
x 8,
1
x
.
2
Ответ: 1
2
; 8.
14.
Типы и методы решения логарифмических уравнений.3) Логарифмические уравнения, сводящиеся к квадратным
уравнениям.
Решение:
В
найденной
области
допустимых
переменной x преобразуем уравнение,
свойства логарифмов.
Пример №2
lg(10x) lg(0,1x) lgx 3 3
значений
используя
D(log a ) 0; , a 0 , a 1, то
lg(10x) lg(0,1x) lgx 3 3,
Т.к.
(lg10 lgx) (lg0,1 lgx) lgx 3 3,
10x 0,
0,1x 0,
x 3 0;
(1 lgx) (lgx 1) 3lgx 3,
(1 lgx) (lgx 1) 3(lgx 1),
(1 lgx) (lgx 1) 3(lgx 1) 0,
(lgx 1) (lgx 2) 0,
lgx 1 0, lgx 1,
lgx 2 0; lgx 2;
x 10,
x 100.
x 0,
x 0,
x 0;
x 0.
С учётом области допустимых значений
получим:
х 0,
x 10,
x 100;
x 0,
x 10,
x 0,
x 100;
x 10,
x 100.
Ответ:
10; 100
15.
Типы и методы решения логарифмических уравнений.4) Логарифмические уравнения, сводящиеся к рациональным
уравнениям.
Решение:
Пример №1
1
1
2
2log 3 x 3 log 3 x 1
1
1
2.
2log 3 x 3 log 3 x 1
Пусть
log 3 x t, тогда
1
1
2,
2t 3 t 1
Вернёмся к переменной х
Т.к.
D(log a ) 0; , a 0 , a 1, то
4t 2 13t 10
0,
(2t 3)(t 1)
x 0,
log 3 x 1,25,
log 3 x 2;
x 0,
1,25
x 3 ,
x 3 2 ;
t 1,25,
t 2,
t 1,5 ; t 1;
x 0,
x 4 243 ,
x 0,
x 9;
x 4 243 ,
x 9.
t 1,25 ,
t 2.
Ответ:
4
243; 9.
16.
Типы и методы решения логарифмических уравнений.4) Логарифмические уравнения, сводящиеся к рациональным
уравнениям.
Решение:
Пример №2
2log x 27 log 27x 1.
2log x 27 log 27x 1
D(log a ) 0; , a 0 , a 1, то x 0,
x 1.
В найденной области допустимых значений
Т.к.
переменной х преобразуем данное уравнение и
получим:
2
log 27 x 1.
log 27 x
x 0, x 1,
2
x
27
,
x 0, x 1,
t 2,
t 1.
x 27;
Пусть log 27x t, тогда
2
t 1,
t
t 2 t 2 0,
Вернёмся к переменной х:
x 0, x 1,
log 27 x 2,
log x 1;
27
x 0, x 1,
2
x 27 ,
x 27;
x 27 2 ,
x 27.
Ответ:
27 2 ;27.
17.
Типы и методы решения логарифмических уравнений.5) Логарифмические уравнения с переменной в основании и
под знаком логарифма.
Решение:
log x
2
2
Т.к.
7x 13 log x 2 2 1.
D(log a ) 0; , a 0 , a 1, то
x 2 7x 13 0,
x 2 0,
x 2 1;
x R,
x 2,
x 3;
x 2,
x 3.
В найденной области допустимых значений
переменной х преобразуем уравнение и получим:
log x 2 2 log 2 x
Пример №1
2
7x 13 1,
log x 2 (x 7x 13) 1,
2
x 2 7x 13 x 2,
x 2 8x 15 0,
log x
2
2
7x 13 log x 2 2 1
С учётом области допустимых значений
переменной х получим:
x 2,
x 3,
x 3,
x 5;
x 2,
x 3,
x 3,
x 2,
x 3,
x 5;
x 5.
x 3,
x 5.
Ответ:
5.
18.
Типы и методы решения логарифмических уравнений.5) Логарифмические уравнения с переменной в основании и
под знаком логарифма.
Решение:
Т.к.
Пример №2
log (x
D(log a ) 0; , a 0 , a 1, то
(x 4) 2 0,
x 8x 16 0, x 7,
7 x 0,
x 2 2 ,
3x 8 0,
3x 8 1;
3
x 3;
2
5
2
2 3 x 7,
x 3,
x 4.
2
8x 16) log 3x 8 (7 x) 0
С учётом области допустимых
значений переменной х получим:
В найденной области допустимых значений переменной х
уравнение равносильно совокупности:
log 5 (x 2 8x 16) 0,
log 3x 8 (7 x) 0;
(x 4) 1,
7 x 1;
x 4 1,
x 4 1,
7 x 1;
x 3,
x 5,
x 6.
2
2
2 3 x 7,
x 3,
x 4,
x 3,
x 5,
x 6;
x 5,
x 6.
Ответ:
5;6.


















 mathematics
mathematics








