Similar presentations:
Интегральное исчисление (лекция 1)
1.
Интегральное исчисление1. Понятие первообразной функции.
2. Неопределенный интеграл и его свойства.
3. Таблица основных интегралов.
Попова Виктория Романовна, к.п.н., доцент кафедры
бизнес-информатики и математики
2.
1. Понятие первообразной функции.Начнем изучение темы «Понятие первообразной» с решения следующей
задачи.
Задача. По прямой движется материальная точка, скорость которой в
момент времени t задается формулой v 3t 2. Найдите закон движения.
Решение. Пусть s(t) – закон
движения. надо найти функцию,
2
производная которой равна v 3t . Т.к. v s / t , то s / t 3t 2. Т.е.
s t t 3 .
Эта задача решена верно, но не полно.
Эта задача имеет бесконечное множество решений.
s t t 3
s / t 3t 2
s t t 3 1
s / t 3t 2
s / t 3t 2
s t t 3 5
/
2
1
3
s
t
3t
s t t
2
можно сделать вывод, что любая функция вида
решением данной задачи, где C любое число.
s t t 3 С
является
3.
1. Понятие первообразной функции.При решении задачи, мы, зная производную функции, восстановили ее
первичный образ.
Эта операция восстановления – операция интегрирования.
Восстановленная функция – первообразная (первичный образ функции):
операция
дифференцирования
функция у = F(x) первообразная
функция у = f(x) производная
операция
интегрирования
Определение. Функция F(x) называется первообразной от функции f(х)
на множестве Х, если Fʹ(x) = f(x) или dF(x) = f(x)dx.
Основное свойство первообразной. Если функция F(x) является
первообразной для функции f(x), то F(x) + С, также является
первообразной для функции f(x).
Доказательство. Т.к. функция F(x) является первообразной для функции
f(x), то F(x)ʹ = f(x). Вычислим производную для (F(x) + С)ʹ:
(F(x) + С)ʹ = (F(x))ʹ + (С)ʹ = f(x) + 0 = f(x). Следовательно, F(x) + С –
первообразная функции f(x).
4.
1. Понятие первообразной функции.Теорема. Если две различные функции F(x) и Ф(х) являются
первообразными для функции f(x), то они отличаются друг от друга только
на произвольную постоянную (константу).
Доказательство. Т.к. функции F(x) и Ф(х) являются первообразными для
функции f(x), то F(x)ʹ = f(x) и Ф(x)ʹ = f(x). Вычислим производную для
(F(x) – Ф(х))ʹ:
(F(x) – Ф(х))ʹ = (F(x))ʹ - (Ф(х))ʹ = f(x) – f(x) = 0.
Следовательно, F(x) – Ф(х) = С, т.к. (С)ʹ = 0. Другими словами, F(x) = Ф(х)
+ С.
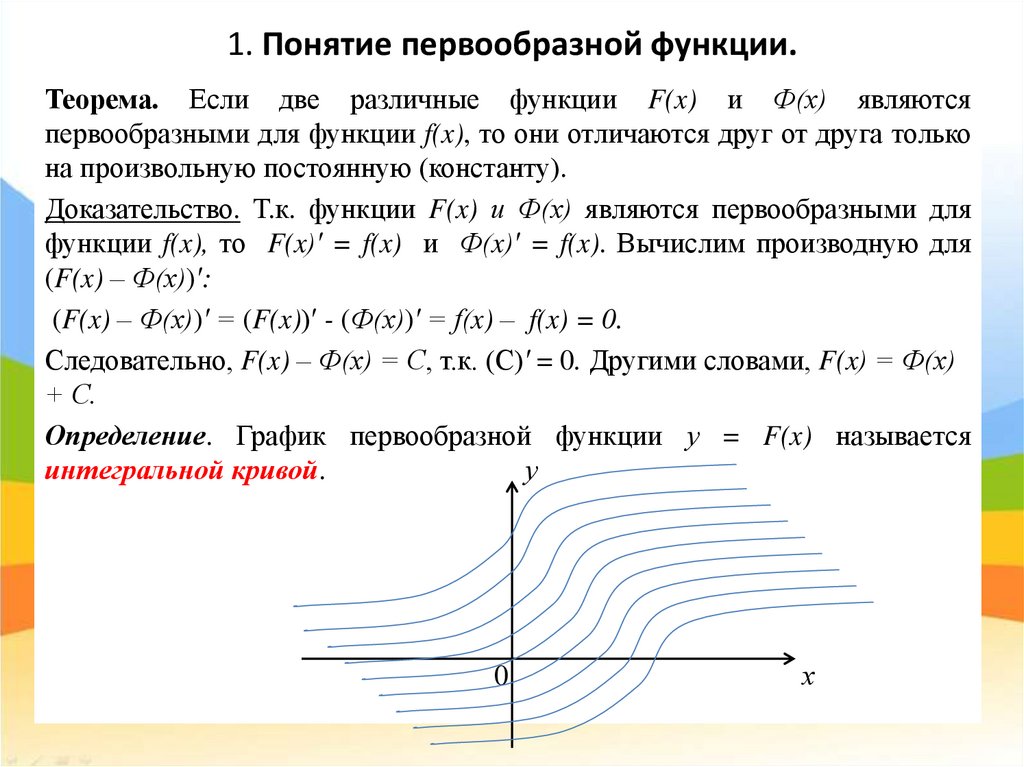
Определение. График первообразной функции у = F(x) называется
интегральной кривой.
у
0
х
5.
1. Понятие первообразной функции.Замечание. Первообразная – это родитель производной: F(x)ʹ = f(x).
Правила вычисления первообразных
Правило 1. Если F(x) есть первообразная для f(x), а G(x) – первообразная
для g(x), F(x) + G(x) есть первообразная для f (x) + g(x).
Правило 2. Если F(x) есть первообразная для f(x), а k-постоянная, то
функция kF(x) – первообразная для kf(x).
Правило 3. Если F(x) есть первообразная для f(x), а k и b – постоянные ,
причем k не равно 0, то 1 F kx b есть первообразная для f(kx+b).
k
Замечание. Вычисление первообразной заключается в нахождении
неопределенного интеграла, а сам процесс называется интегрированием.
6.
2. Неопределенный интеграл и его свойства.Определение. Совокупность всех первообразных функций F(x) + C для
функции f(x) называется неопределенным интегралом функции у = f(x) и
обозначается f x dx F x C .
знак интеграла
f x подинтегральная функция
f x dx подинтегральное выражение
Определение. Операция отыскания неопределенного интеграла некоторой
функции называется интегрированием.
Основные свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному
выражению:
d f ( x )dx f ( x )dx
2. Производная неопределенного интеграла равна подынтегральной
функции:
f ( x)dx f ( x).
Замечание. Таким образом, правильность интегрирования проверяется
дифференцированием.
7.
2. Неопределенный интеграл и его свойства.3. Неопределенный интеграл от дифференциала некоторой функции равен
сумме этой функции и произвольной постоянной:
dF ( x) F ( x ) C .
4. Постоянный множитель можно выносить за знак интеграла:
af ( x)dx a f ( x)dx.
5. Неопределенный интеграл от алгебраической суммы конечного числа
непрерывных функций равен алгебраической сумме интегралов от
слагаемых функций:
f ( x) g( x) dx f ( x)dx g( x)dx.
6. Если f ( x ) dx F ( x ) C , то f (u) du F (u) C , где u = φ(x) −
произвольная функция, имеющая непрерывную производную.
Замечание.
Данное
свойство
называется
инвариантностью
неопределенного интеграла.
8.
Таблица простейших интегралов1. 0 du C;
2. 1 du u C; 1;
1
u
3. u du
C,
1
1
1
4. 2 du C;
u
u
1
5.
du 2 u C ;
u
1
6. du ln u C;
u
u
a
7. a du
C;
ln a
u
8. e udu e u C;
9. sin udu cos u C;
10. cos udu sin u C;
1
11.
du tgu C ;
2
cos u
1
12. 2 du ctgu C;
sin u
9.
Таблица простейших интегралов1
1
u
13. 2
du arctg C ;
2
u a
a
a
14.
1
u
du arcsin C ;
2
2
a
a u
du
1
u a
15. 2
ln
C;
2
u a
2a u a
16.
du
u a
2
2
ln u u2 a 2 C .
10.
Вычислениеинтегралов
с
помощью
преобразования подынтегрального выражения к
табличной форме и использования свойств
неопределенного
интеграла
называется
непосредственным интегрированием.
Вспомогательные сведения
1. a m a n a m n ;
am
m n
2.
a
;
n
a
1
n
3.
a ;
n
a
4.
n
m
a a n.
m
11.
2. Неопределенный интеграл и его свойства.Примеры. Используя таблицу и свойства интегралов, найти интегралы.
dx
1
1.
воспользуемся формулой (3) :
а т х 5 dx
x
ат
воспользуемся формулой (3) таблицы
n 1
n
u
u du
C
n 1
x 5 1
x 4
1
C
C 4 C
5 1
4
4x
2.
5
производных
воспользуемся формулами (3) и (7)
х
x
2 х 7 dx 2 xdx 7 dx таблицы производных
n 1
u
u
a
n
u
u du
C
и a du
C
n 1
ln a
x1 1 7 x
2x 2 7 x
7x
2
2
C
C x
C
1 1 ln 7
2
ln 7
ln 7
12.
2. Неопределенный интеграл и его свойства.Примеры. Используя таблицу и свойства интегралов, найти интегралы.
n
5
5
m n
3.
m
x dx воспользуемся формулой (4) :
a а х 2 dx
воспользуемся формулой (3) таблицы
n 1
n
u
u du
C
n 1
5
1
2
7
2
производных
7
x
x
2
2 7
C
C x2 C
x C
5
7
7
7
1
2
2
воспользуемся формулой (13)
dx
dx
4. x 2 16 x 2 4 2 таблицы производных
du
1
u
arctg
C
2
2
a
a
u a
1
x
arctg C
4
4











 mathematics
mathematics








