Similar presentations:
Thermal Diffusion Equation
1. Thermal Diffusion Equation
The total heat flow rate (heating power) leaving out of a closed surface S enclosing volume V:Heat capacity per unit volume
Total thermal energy concentrated in volume V
Stokes divergence theorem:
Dim {D} = m2/s
Thermal diffusivity
In 1D:
3D thermal diffusion equation
Equation in 3D
Specific heat capacity
2. 1D Thermal Diffusion due to Periodic Heating Waves
Trial wave-likesolution:
angular frequency
General solution for x > 0:
3.
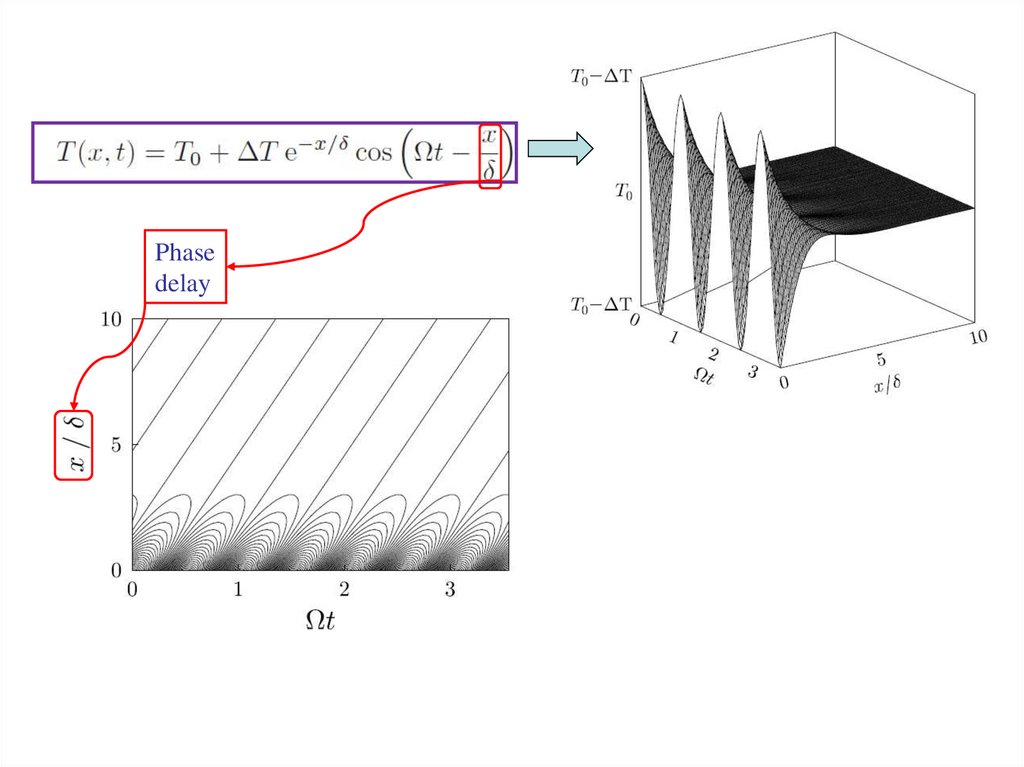
Boundary condition – the ground surface is under periodic temperature wave:From general solution of thermal diffusion equation:
Frequency-dependent coefficients become::
Hence, the solution for x ≥ 0 becomes:
Spatio-temporal temperature
evolution
Constant
surface
temperature
at t = 0
Spatially
decaying
temperature
amplitude
Temperature
modulation
rate
Phase
delay
Heat diffusion
or “skin” depth:
4.
Phasedelay
5.
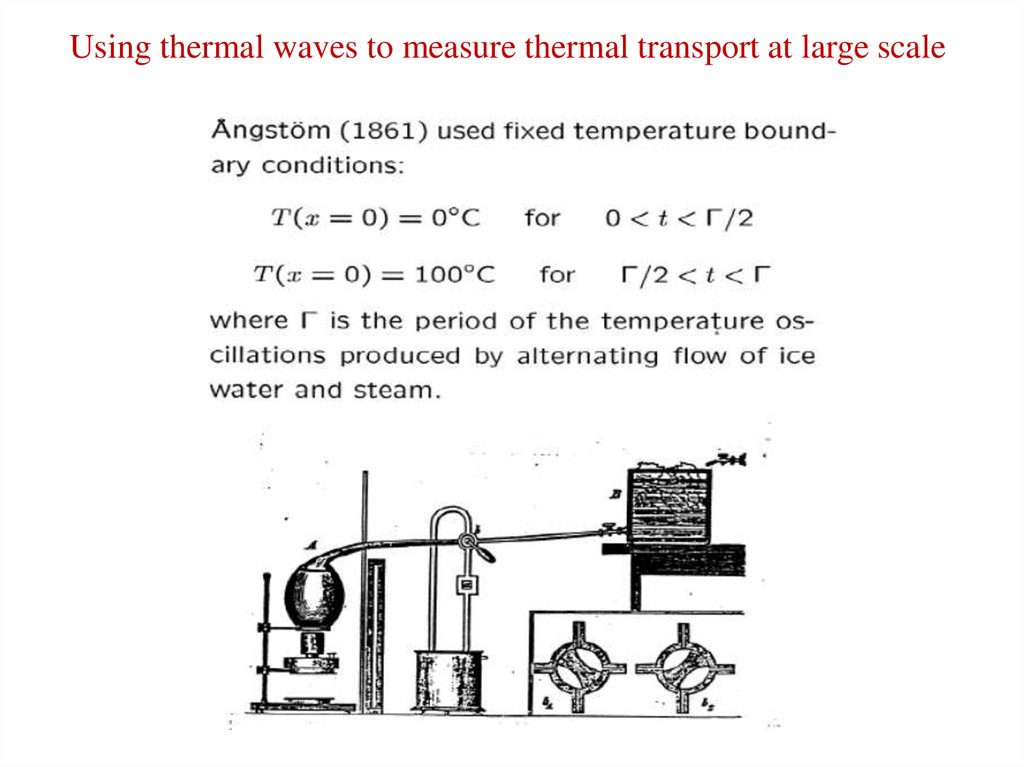
Using thermal waves to measure thermal transport at large scale6. Femtosecond laser-based time-domain thermoreflectance (TDTR) setup in our lab
7.
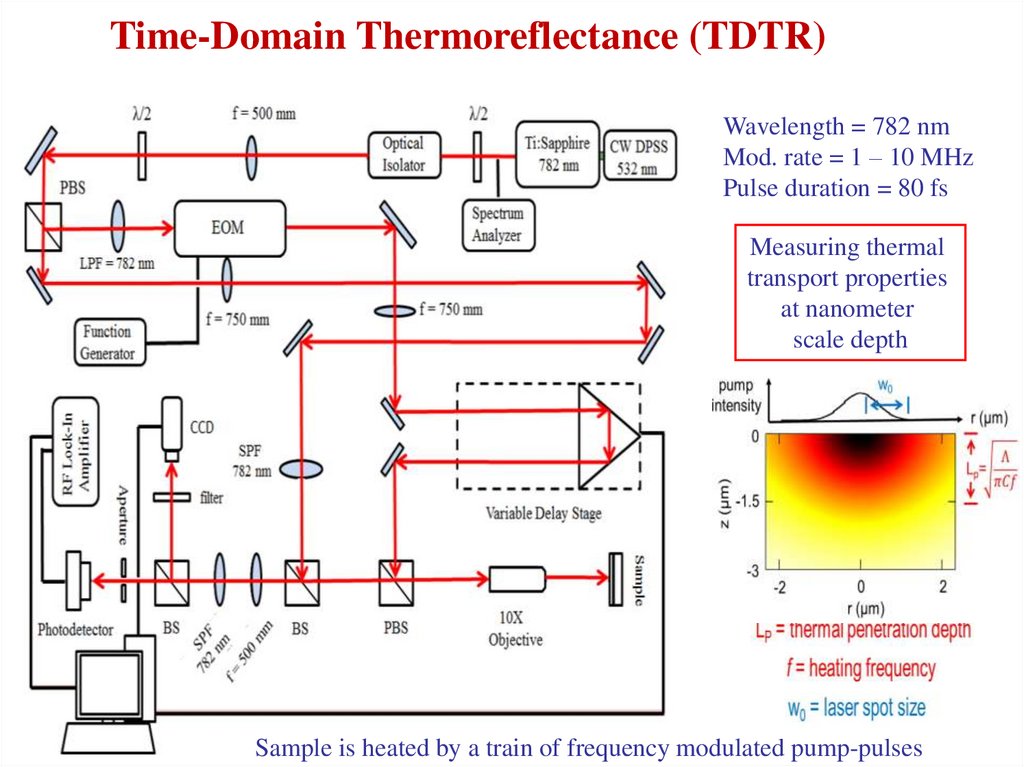
Time-Domain Thermoreflectance (TDTR)Wavelength = 782 nm
Mod. rate = 1 – 10 MHz
Pulse duration = 80 fs
Measuring thermal
transport properties
at nanometer
scale depth
Sample is heated by a train of frequency modulated pump-pulses
8.
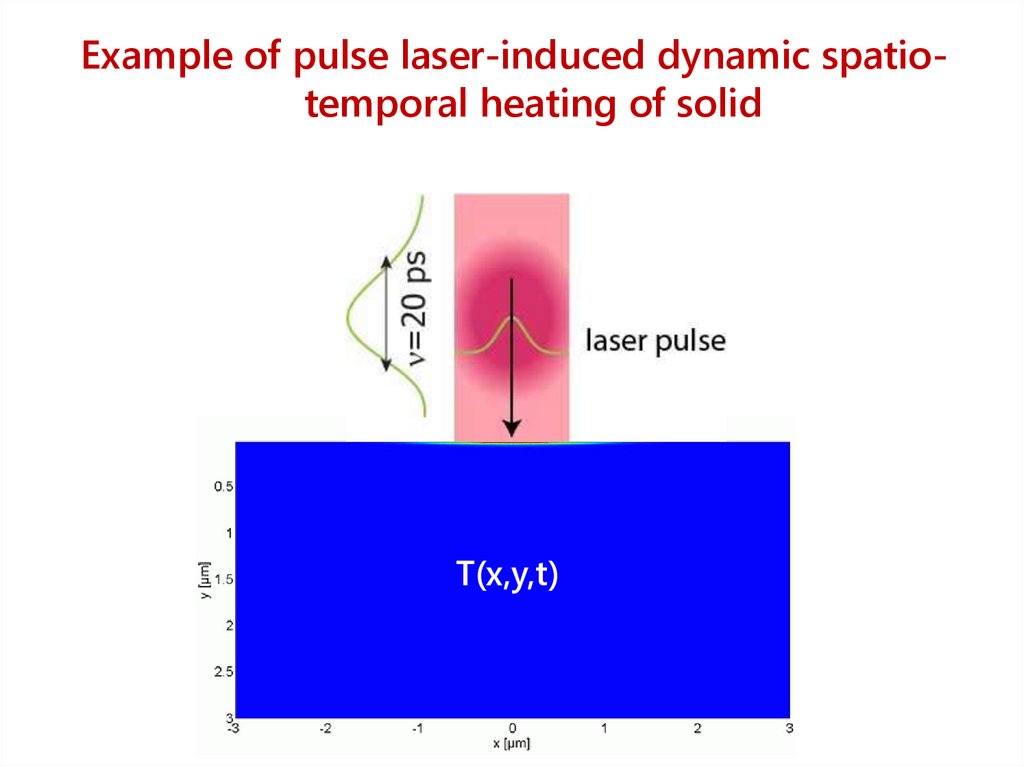
Example of pulse laser-induced dynamic spatiotemporal heating of solidT(x,y,t)
9. Steady State Regime
Then:If
(Laplace Equation)
Temperature does not vary with time, but heat spatial heat flux is not vanished:
x=L
x=0
heat flux
T1
>
Heat flux =
T2
10. Thermal Diffusion in Spherically Symmetrical Systems
Laplacian in spherical coordinates:Equation of heat diffusion equation in spherical radial direction:
In steady state:
=
constant
11. Cooking “spherical” cold chicken in a surrounding hot oven
HotT=T1
(general
Oven solution)
a
Cold
chicken
T=T0
Cooking “spherical” cold chicken in a
surrounding hot oven
(boundary condition)
(initial condition)
12.
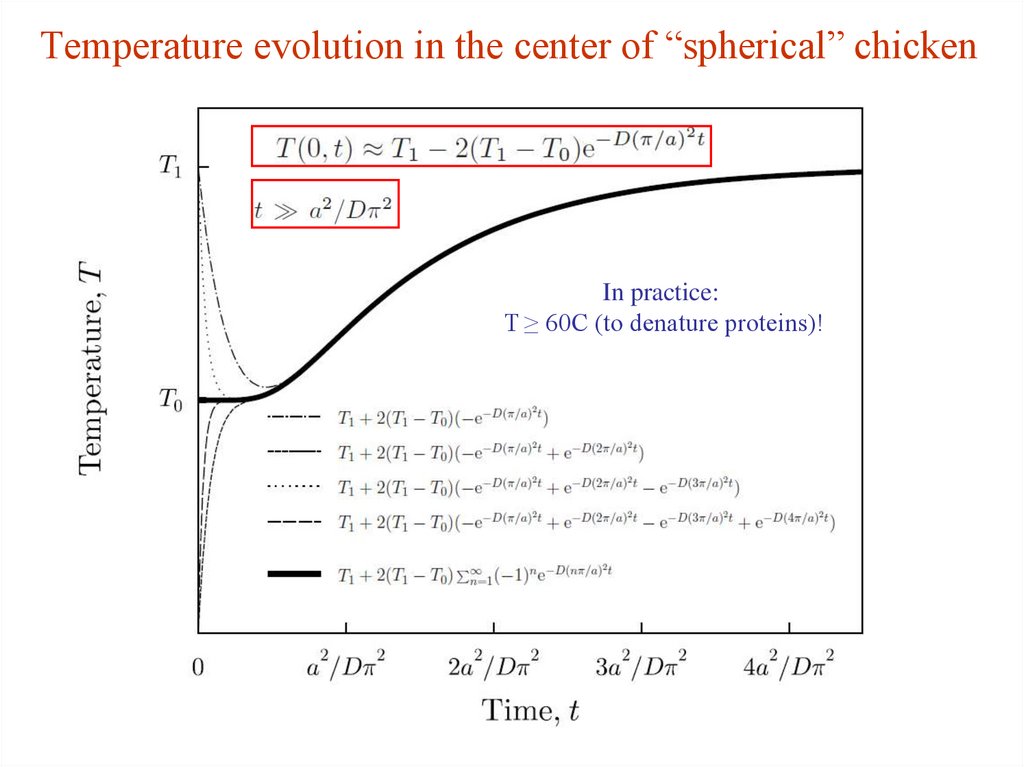
Assume wave-like solutions:Temperature evolution in the center of chicken:
13. Temperature evolution in the center of “spherical” chicken
In practice:T ≥ 60C (to denature proteins)!
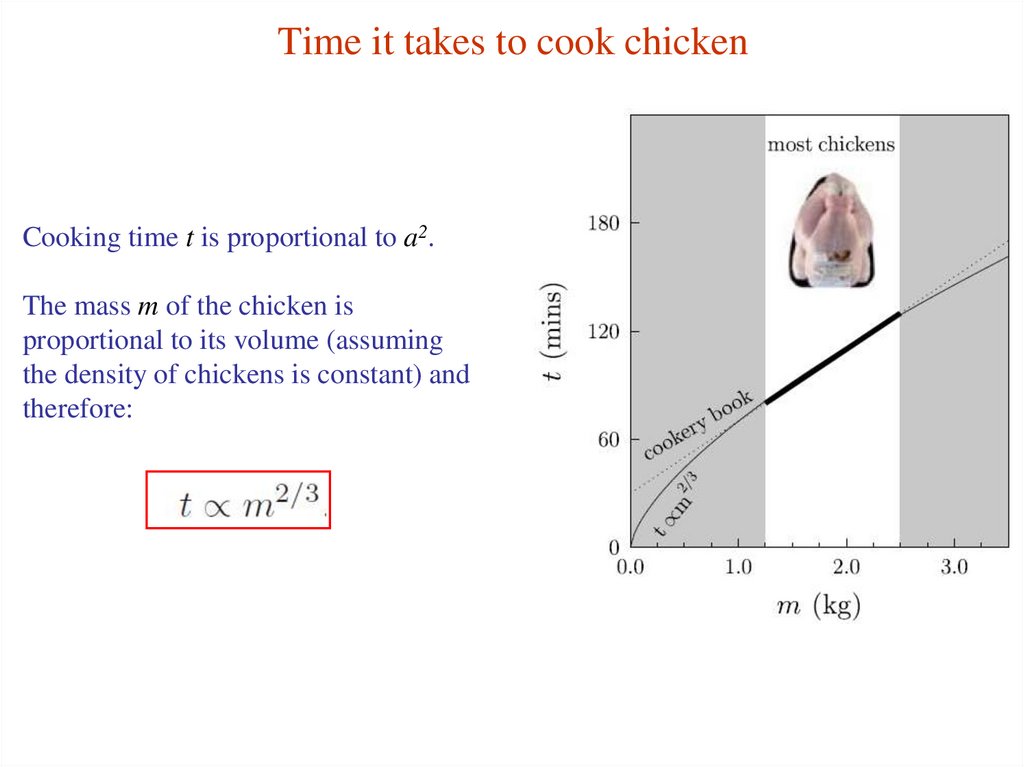
14. Time it takes to cook chicken
Cooking time t is proportional to a2.The mass m of the chicken is
proportional to its volume (assuming
the density of chickens is constant) and
therefore:








 mathematics
mathematics








