Численное дифференцирование

1. Численное дифференцирование

2. Постановка задачи

Не каждую функцию можно
дифференцировать аналитически.
Если функция задана :
► слишком громоздким выражением;
► таблично;
► неявно (н-р, численным алгоритмом);
то приходится искать другие способы
дифференцирования.

3. Постановка задачи

Задача численного дифференцирования
состоит в приближенном вычислении
производных функции f(x) в
некоторой точке по заданным в
конечном числе точек значениям
этой функции.

4. Постановка задачи

Таким образом заданные функции
называются табличными, или
сеточными функциями. Считаем, кроме
того, что рассматриваемая сеточная
функция есть проекция (или
ограничение) на сетку некоторой гладкой
нужное число раз непрерывно
дифференцируемой функции f(x).

5. Постановка задачи

Как правило, значения функции f(x) в
точках вычисляются не точно, а с
каким-то приближением. Например,
элементарные трансцендентные
функции вычисляются с помощью
рядов, причем ряды заменяются
конечными суммами.

6. Определение производной

Производная функции есть предел отношения
приращения функции к приращению
независимой переменной при стремлении к
нулю приращения независимой переменной.
df
f
lim
dx x 0 x

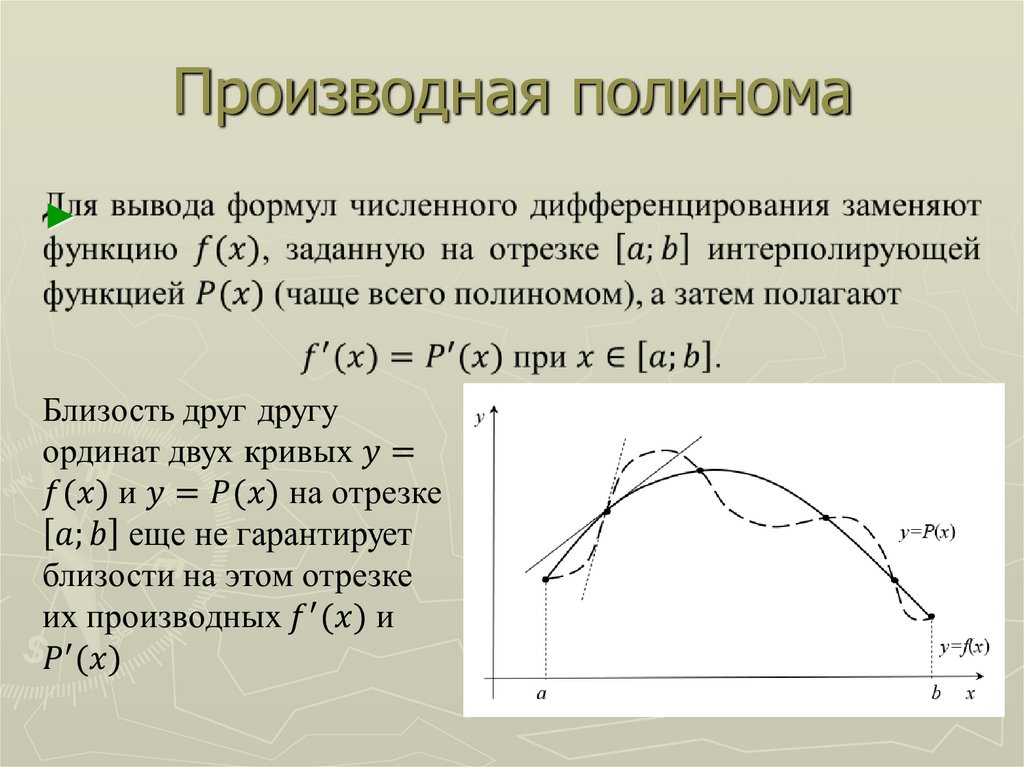
7. Идея численного дифференцирования

Аппроксимируем производную - заменим
предел приближенным значением:
df f
dx x
Чтобы вычислить правую часть,
необходимо знать значение функции
хотя бы в двух точках.

8. Формулы разностной двухточечной аппроксимации

df ( x0 ) f ( x0 ) f ( x0 x)
Аппроксимация
(1) «назад»
dx
x
df ( x0 ) f ( x0 x) f ( x0 )
(2) Аппроксимация
«вперед»
dx
x
df ( x0 ) f ( x0 x) f ( x0 x)
Центральная
(3) аппроксимация
dx
2 x

9. Графическая иллюстрация двухточечной аппроксимации

10. Разностная двухточечная аппроксимация

В случае, если Δx постоянно на некотором
рассматриваемом отрезке [a;b]:
Δx = h,
то говорят о шаге дискретизации функции
или шаге равномерной сетки.
Формулы (1) – (3) называют также
конечно-разностными формулами, (1)
и (2) – на двухточечном шаблоне, (3) –
на трехточечном.

11. Пример 1. Вычислить точное и приближенное (тремя методами) значения производной функции y=x2 в точке x=1 с шагом h=1 и h=0.001.

Аналитическое решение: y'=2x , y'(1)=2,
Численное решение для шага: h=1
y (1) y (1 1) 1 0
1
yh 1
1
1
y (1 1) y (1) 4 1
3
yh 2
1
1
y (1 1) y (1 1) 4 0
2
yh 3
2
2

12. Пример 1.

Аналитическое решение: y'=2x , y'(1)=2,
Численное решение для шага h=0.001

13. Пример 2. Вычислить точное и приближенное (тремя методами) значения производной функции y=3/x в точке x=-1 с шагом h=0.5.

Аналитическое решение: y'=-3/x2 , y'(-1)=-3,
Численное решение для шага: h=0.5
y ( 1) y ( 1 0.5) 3 2
2
yh 1
0.5
0.5
y ( 1 0.5) y ( 1) 6 3
6
yh 2
0.5
0.5
y ( 1 0.5) y ( 1 0.5) 6 2
4
yh 3
1
1

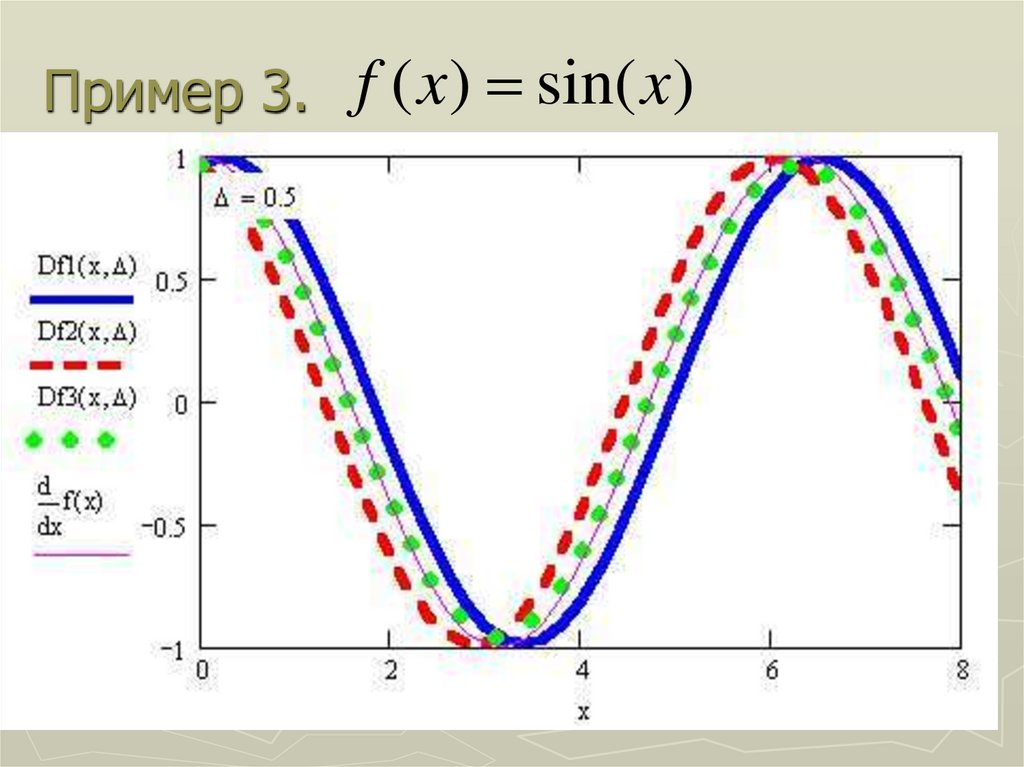
14. Пример 3.

f ( x) sin( x)

15. Погрешность численного дифференцирования

Как свидетельствуют рассмотренные примеры,
из трех формул аппроксимации
(приближения) производной лучший
результат дает последняя – центральная.
Применяя разложение в ряд Тейлора:
( x x0 )2
f ( x) f ( x0 ) ( x x0 ) f x0
f ( x0 ) (( x x0 )3 )
2
в точках x0 и x0+Δx, можно заключить, что (1)
и (2) формулы имеют первый порядок, а (3) –
второй порядок точности относительно Δx.

16. Погрешность численного дифференцирования

Погрешность метода по формулам (1) и (2) равна
M 2h
f ( x)
2
(*)
Погрешность метода по формулам (3)
M 3h
f ( x)
6
где
2
(**)
M 2 max f ( x) , M 3 max f ( x)
x a ,b
x a ,b

17. Графики зависимости погрешностей примера 2 от значения Δx

18. Погрешность численного дифференцирования

Зависимость погрешностей от значения Δx
иллюстрировались при достаточно больших
Δx [0.05;0.3].
Насколько уменьшится погрешность при
существенном уменьшении Δx? Например, до
10-20?

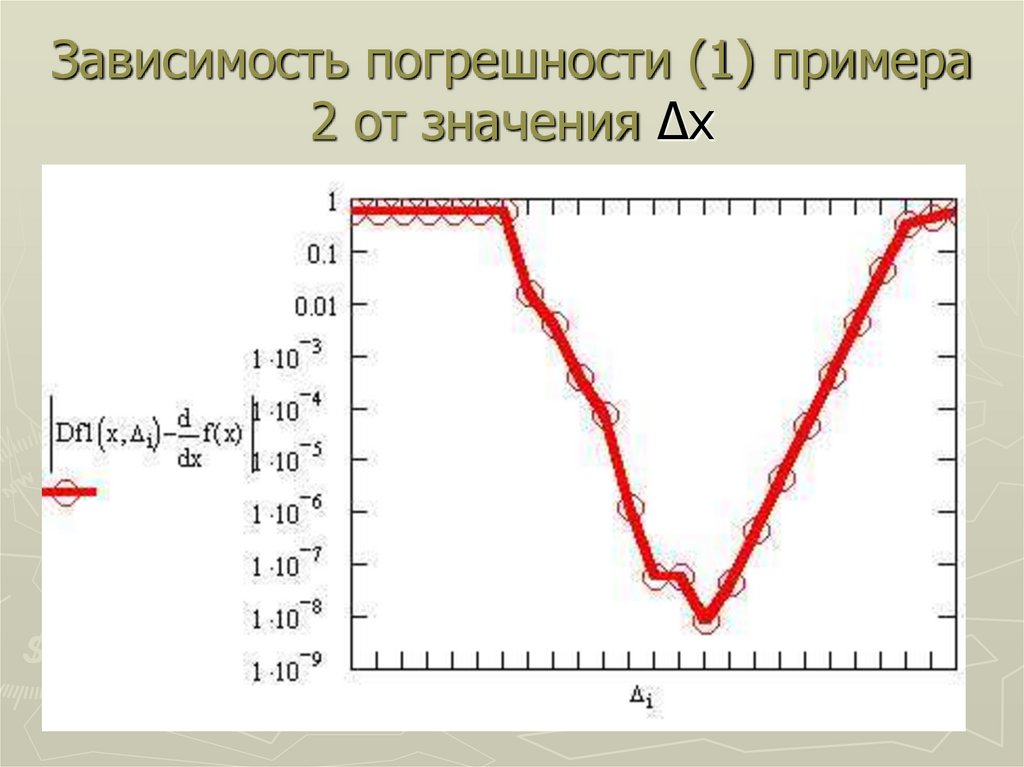
19. Зависимость погрешности (1) примера 2 от значения Δx

20. Погрешность численного дифференцирования

Рост погрешности при очень малых Δx кажется
неожиданным. Это связано с тем, что вычисление
значений функции f(x) сопряжены с
неустранимыми погрешностями, в частности,
обусловленными дискретным представлением
чисел. Поэтому при очень малом шаге разностные
формулы означают вычитание друг из друга
близких чисел. В этом случае ошибки
вычисления функции f(x) становятся
доминирующими, и приводят к существенному
росту ошибки вычисления разностной
производной.

21. Вычислительная погрешность

При ее оценке большую роль играет машинное ε мера относительной погрешности машинного
округления, возникающей из-за конечной
разрядности мантиссы при работе с числами в
формате с плавающей точкой.
По определению машинным ε называют
наибольшее из чисел, для которых в рамках
используемой системы вычислений, выполнено
1 + ε = 1.

22. Выбор шага дискретизации

Практически важным является вопрос о
выборе шага h для дифференцирования
функции. Ограничение сверху
накладывается формулой приближенного
дифференцирования, а снизу –
точностью известных значений функции
f(x) и ошибками округления.

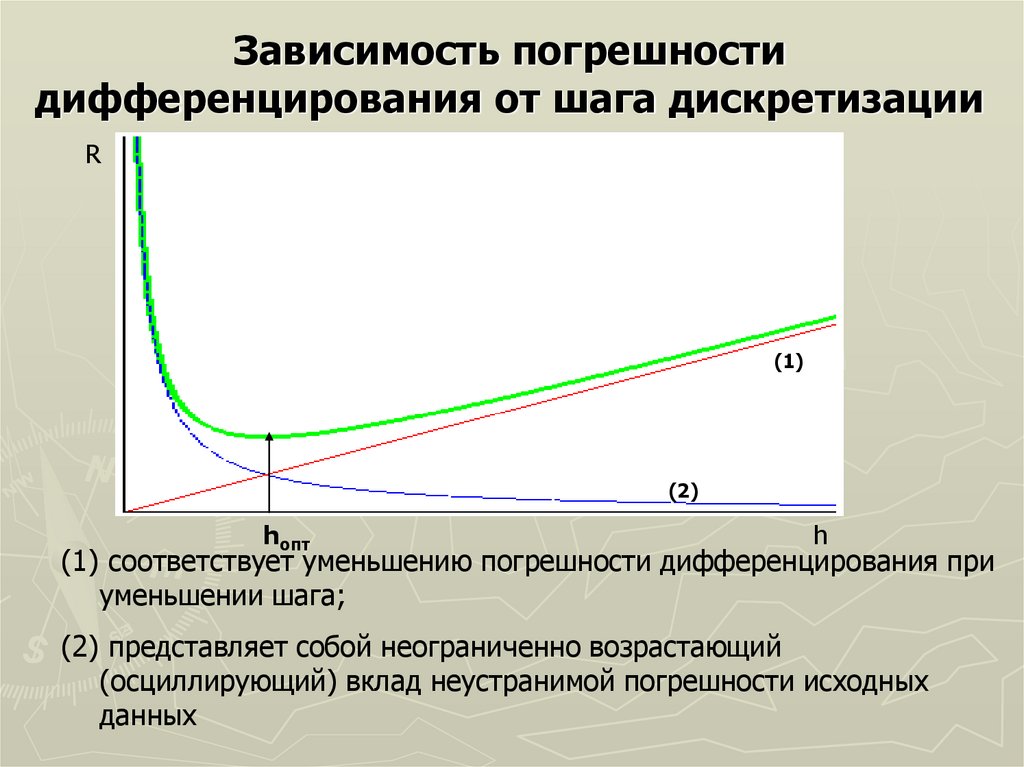
23.

Зависимость погрешности
дифференцирования от шага дискретизации
R
(1)
(2)
hопт
h
(1) соответствует уменьшению погрешности дифференцирования при
уменьшении шага;
(2) представляет собой неограниченно возрастающий
(осциллирующий) вклад неустранимой погрешности исходных
данных

24. Выбор шага дискретизации

Оптимальное значение шага h отвечает
ситуации равенства двух составляющих
погрешностей: исходных данных и
аппроксимации.
На практике это значение точно не
определяется, желательно знать его
порядок.

25. Некорректность численного дифференцирования

Численное дифференцирование –
некорректная задача, так как
отсутствует устойчивость решения.
Вычитание близких значений функции
приводит к уничтожению первых
значащих цифр, т.е. к потере части
достоверных знаков числа. А так как
значения функции обычно известны с
определенной погрешностью, то все
значащие цифры могут быть потеряны.

26. Некорректность численного дифференцирования

Отсюда следует вывод: значение шага
следует выбирать "не очень
большим и не очень малым", иначе
ошибки приближения или
вычисления f(x) сделают результат
дифференцирования неправильным!

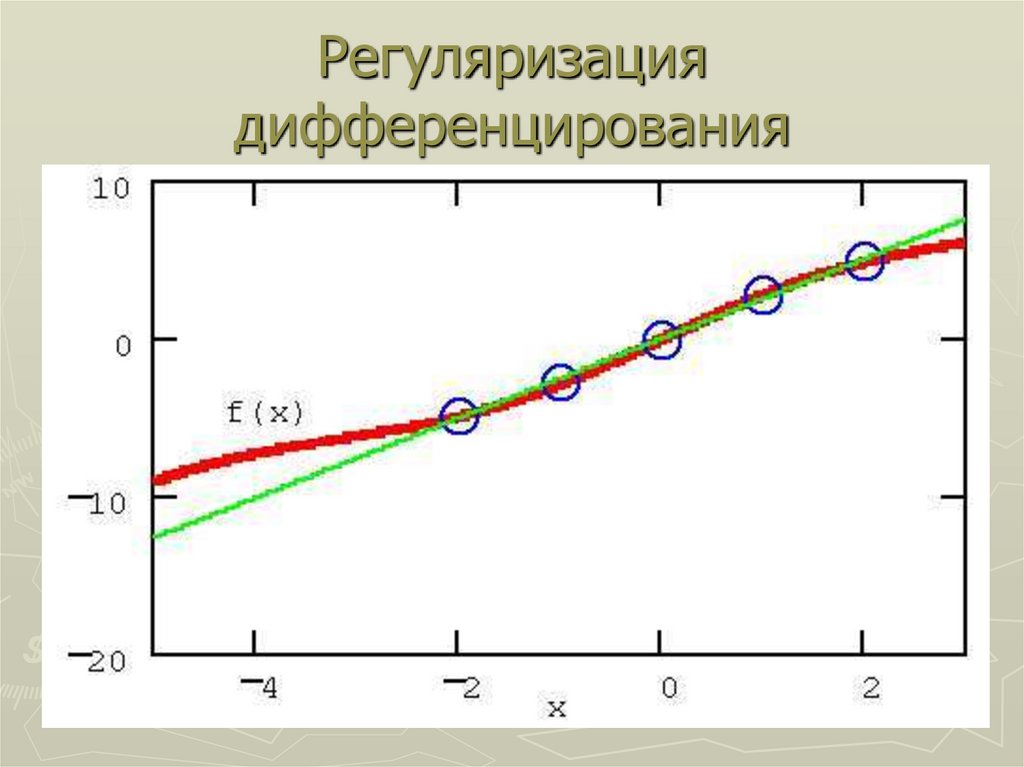
27. Регуляризация дифференцирования

Для решения некорректных задач А.Н. Тихоновым
предложен метод, называемый регуляризацией.
Применительно к задаче численного
дифференцирования его простейшая
модификация, называемая алгоритмом
регуляризации по шагу, может быть
сформулирована следующим образом.
На малом интервале вблизи точки x0
функция f(x) заменяется некоторой
гладкой функцией, осуществляющей
регрессию f(x), например (в простейшем
случае) - прямой линией.

28. Регуляризация дифференцирования

29. Аппроксимация 2-ой производной

Если в разложение функции f(x) в ряд Тейлора
( x x0 )2
f ( x) f ( x0 ) ( x x0 ) f x0
f ( x0 ) (( x x0 )3 )
2
подставить центральную формулу для 1-ой
производной df ( x0 ) f ( x0 x) f ( x0 x)
dx
2 x
получим формулу для расчета 2-ой производной
функции:
f ( x0 ) f ( x0 x) 2 f ( x0 ) f ( x0 x)
(4)
2
2
x
x
2

30. Пример. Вычислить точное и приближенное значения второй производной функции y=x3 в точке x=2 c шагом h=1.

Аналитическое решение: y’’=6x , y’’(2)=12,
Численное решение для шага: h=1.
y (2 1) 2 y (2) y (2 1) 27 16 1
yh
12.
1
1

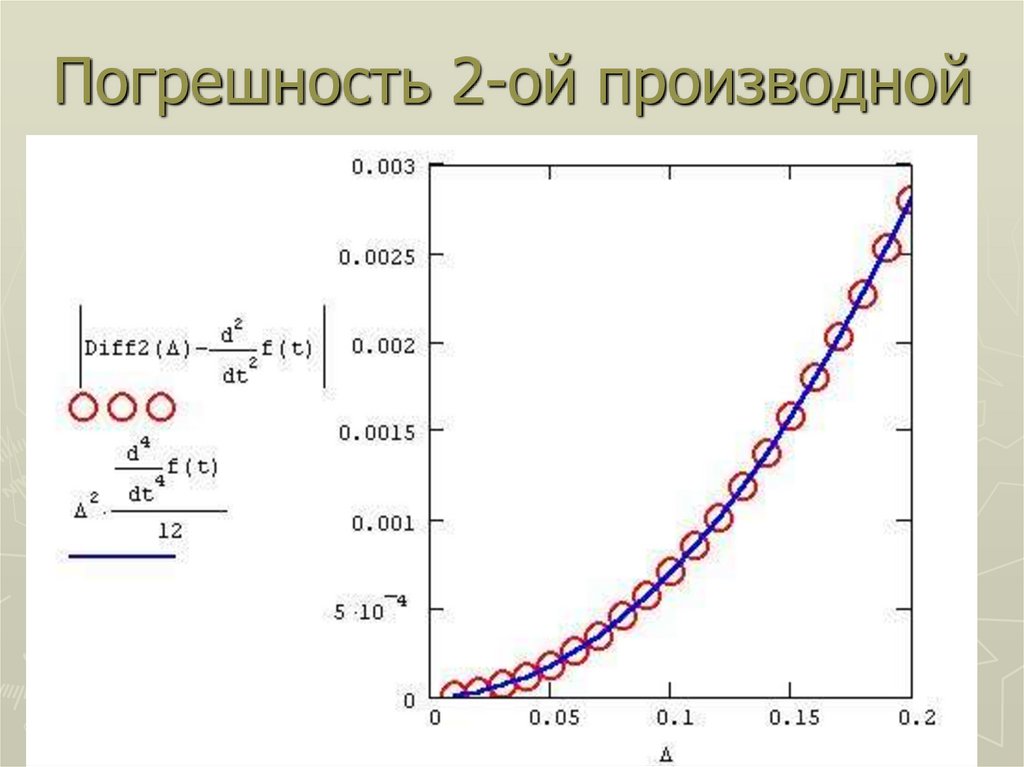
31. Аппроксимация 2-ой производной

Разложив в ряд Тейлора функцию f(x) в
точках x0-Δx, x0 и x0+Δx, можно получить
оценку метода для формулы (4):
2
M 4h
f ( x)
, M 4 max f (4) ( x)
x a ,b
12
(***)
где h=Δx. Таким образом, имеет место
аппроксимация второго порядка.

32. Погрешность 2-ой производной

33. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ НА ОСНОВЕ ИНТЕРПОЛЯЦИОННЫХ МНОГОЧЛЕНОВ

34. Производная полинома

35. Формулы численного дифференцирования, основанные на первой интерполяционной формуле Ньютона

Погрешность (априорная):

36. Численное дифференцирование для равноотстоящих точек на основе интерполяционной формулы Лагранжа

37. Формулы производных на основе интерполяционного полинома Лагранжа

38. Формулы для первой производной в узлах для n=2 (3 точки)

39. Формулы для второй производной в узлах для n=2 (3 точки)