Интерполирование и численное дифференцирование функций

1. Тема. Интерполирование и численное дифференцирование функций

Приближение функций – замена на
интервале [а, b] исходной функции f (x)
некоторой другой функцией P(x):
n
P x ci i x
i 0
Например: φi(x) = sini(x), φi(x) = xi, и т.д.
Исходные данные: xi [a, b], yi = f (xi), i = 0,
1, …, p, x0 = a, xp = b.

2. Приближение функций

Тогда
f (x) = P(x) + R(x),
где R(x) – остаточный член.
Применение: возможность вычислить f (x)
≈ P(x) при x ≠ xi, если:
1. аналитический вид f (x) неизвестен;
2. функция f (x) имеет сложный вид.

3. Приближение функций

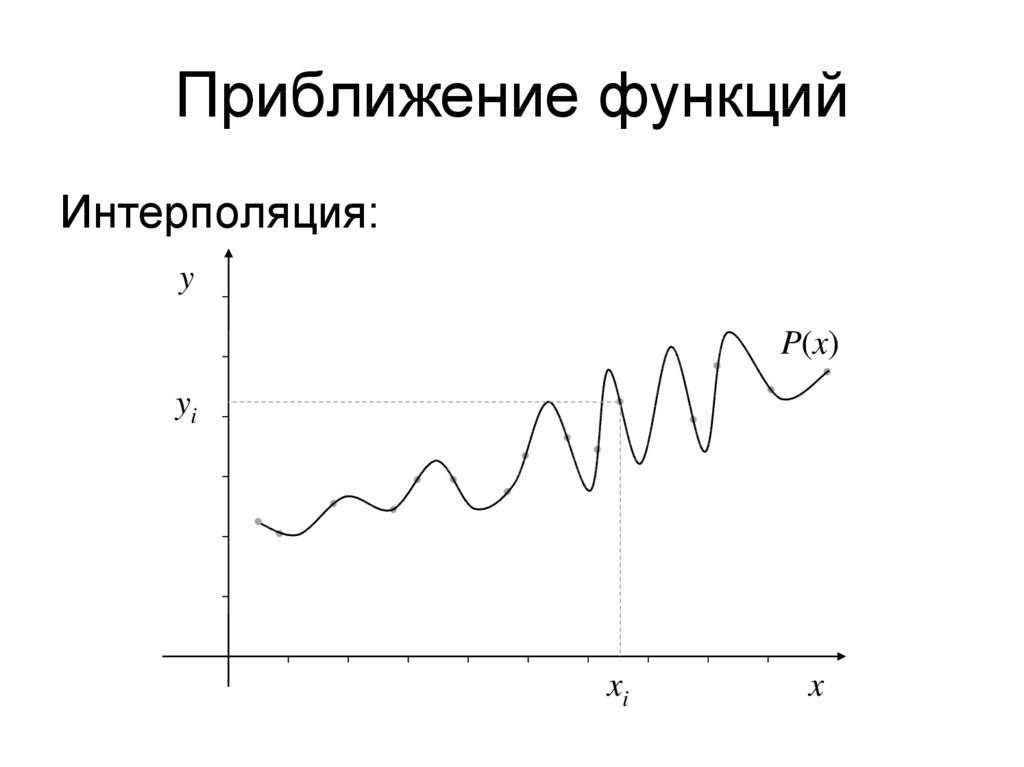
Классификация:
• Интерполяция. Критерий для
определения ci выглядит как P(xi) = yi (p
≥ n, обычно p = n);
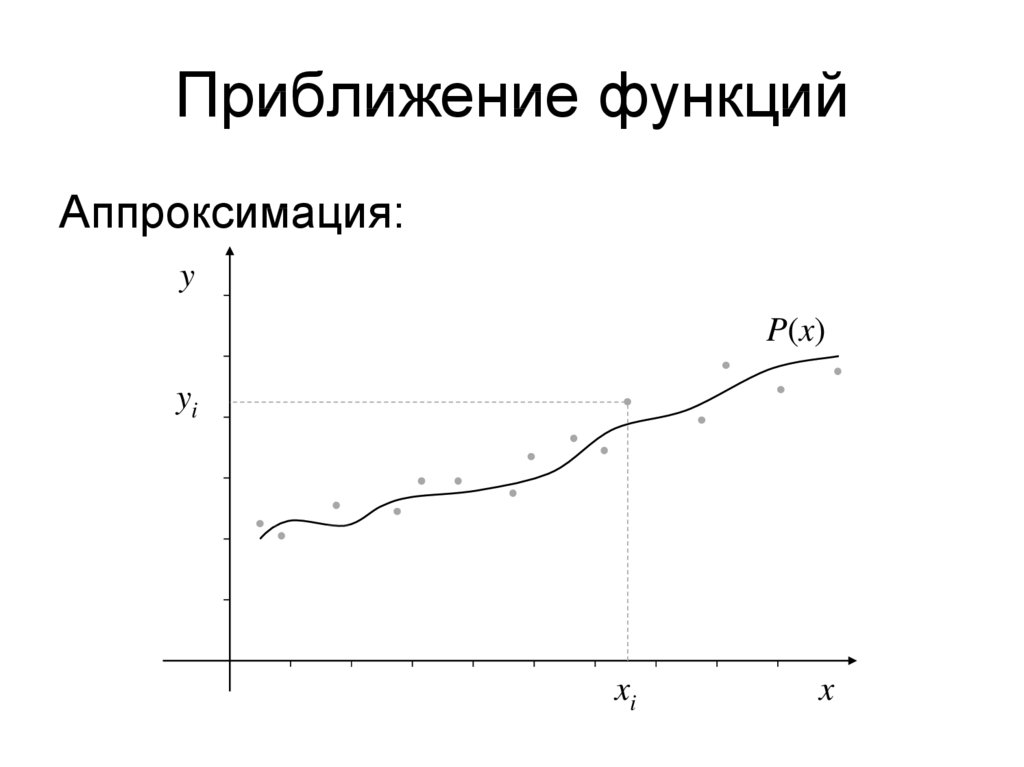
• Аппроксимация (p < n). Критерий для
определения ci выглядит как
1
n
n
y P x
i 0
i
i
2
min
ci

4. Приближение функций

Классификация:
• Экстраполяция – возможность
вычислить f (x) ≈ P(x) при x [a, b].

5. Приближение функций

Интерполяция:
y
P(x)
yi
xi
x

6. Приближение функций

Аппроксимация:
y
P(x)
yi
xi
x

7. Интерполирование функций

Постановка задачи:
p=n
Сетка (табличные значения функции):
{xi}: xi [a, b], i = 0, 1, …, n
x0 = a, xn = b
{yi}: yi = f (xi)
Количество узлов – n + 1.

8. Интерполирование функций

Постановка задачи:
Равномерная сетка:
{xi}: xi = x0 + i h, i = 0, 1, …, n
x0 = a, xn = b
xn x0 b a
h
.
n
n
Система линейно-независимых функций:
φi(x)

9. Интерполирование функций

Постановка задачи:
Требуется определить коэффициенты
сi, i = 0, 1, …, n
таким образом, чтобы
Pn(xi) = yi
Для решения будем использовать
степенные полиномы:
n
i x xi , Pn x ci x i .
i 0

10. Интерполирование функций

Постановка задачи:
Для равномерной сетки
x x0
q
,
h
поэтому
n
i q q i , Pn q ci q i .
i 0

11. Полином Ньютона

c x ,..., x , x x x ,
i 1
i
0
i
i
j 0
j
i 1
Pn x x0 ,..., xi x x j
i 0
j 0
n
xi 1 ,..., x j xi ,..., x j 1
Здесь xi ,..., x j
–
x j xi
разделенные разности j-i-го порядка,
[xi] = yi

12. Полином Ньютона

Для равномерной сетки
i 1
i y0
ci
, i q q j ,
i!
j 0
i y0 i 1
Pn q
q j
i 0 i !
j 0
n
Здесь i y j i 1 y j 1 i 1 y j , 0 y j y j –
конечные разности j-i-го порядка.

13. Полином Лагранжа

ci
yi
xi x j
n
, i x x x j ,
n
j 0
j i
j 0
j i
n
n
n
n
x xj
yi
Ln x n
x x j yi x x
i 0
i 0
j 0
j 0 i
j
x
x
j
i
j
i
j
j 0 i
j i

14. Полином Лагранжа

Для равномерной сетки
ci 1
n i
n
yi
, i q q j ,
i ! n i !
j 0
j i
n
yi
n i
Ln q 1
q
j
i ! n i ! j 0
i 0
j i
n

15. Численное дифференцирование функций

Постановка задачи:
f (x) = P(x) + R(x)
n
P x ci i x
i 0
Определить:
f (k)(x) = (P(x) + R(x))(k) = P(k)(x) + R(k)(x)
P x ci i x
i 0
k
n
k
n
ci i
i 0
k
x

16. Полином Ньютона

Первая производная для неравномерной
сетки:
i 1
Pn x x0 ,..., xi x x j
i 0
j 0
n
i 1 i 1
x0 ,..., xi x xk
i 1
j 0 k 0
k j
n

17. Полином Ньютона

Первая производная для равномерной
сетки:
i
i
1
y0
Pn q
q j
i 0 i !
j 0
n
i
i 1 i 1
1 y0
q k
h i 0 i ! j 0 k 0
k
j
n

18. Полином Ньютона

Вторая производная для неравномерной
сетки:
i 1
Pn x x0 ,..., xi x x j
i 0
j 0
n
i 1 i 1 i 1
x0 ,..., xi x xl
i 2
j 0 k 0 l 0
k j l k
l
j
n

19. Полином Ньютона

Вторая производная для равномерной
сетки:
i
1
i
y0
q j
Pn q
i 0 i !
j 0
1 n i y0 i 1 i 1 i 1
q l
2
h i 2 i ! j 0 k 0 l 0
k j l k
j
l
n

20. Полином Лагранжа

Первая производная для неравномерной
сетки:
n
n
yi
Ln x n
x xj
i 0
jj 0i
x
x
i
j
j 0
j i
n
n
n
yi
n
x xk
i 0
j 0 k 0
x
x
j i k i
i
j
j 0
k j
j i

21. Полином Лагранжа

Первая производная для равномерной
сетки:
n
n
yi
n i
q j
Ln q 1
i ! n i ! j 0
i 0
j
i
n
n
yi
1 n
n i
1
q k
h i 0
i ! n i ! j 0 k 0
j i k i
k j

22. Полином Лагранжа

Вторая производная для неравномерной
сетки:
n
n
yi
Ln x n
x xj
j 0
i 0
x
x
i
j j i
j 0
j i
n
n
n
n
yi
n
x xl
i 0
j 0 k 0 l 0
x
x
j
i
k
i
l
i
j
j 0 i
k j l j
l k
j i

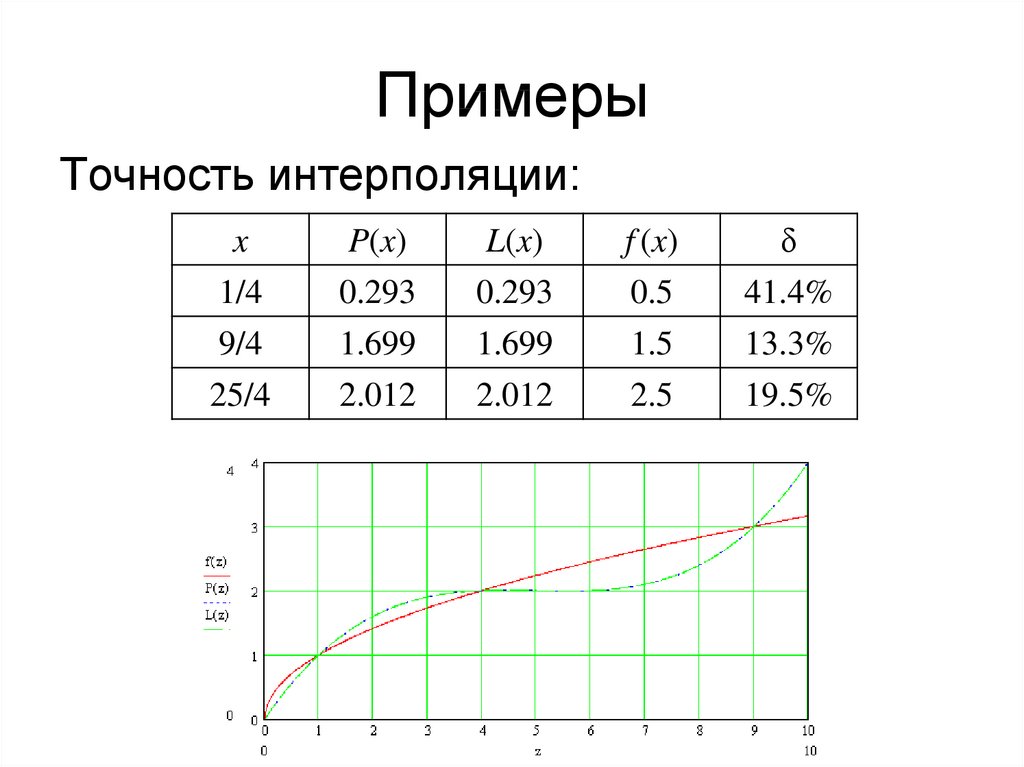
23. Примеры

Полином Ньютона.
f x x
i
x
y
0
0
0
1
1
1
2
4
2
3
9
3
Результирующая сетка: {1/4, 9/4, 25/4}
Далее строим полином P3(x).

24. Примеры

Полином Ньютона.
Разделенные разности:
i
0
1
2
3
X
0
1
4
9
y
0
1
2
3
[xi,xi+1]
1
1/3
1/5
[xi,..,xi+2]
–1/6
–1/60
xi 1 ,..., x j xi ,..., x j 1
xi ,..., x j
x j xi
[xi,..,xi+3]
1/60

25. Примеры

Полином Ньютона.
i
0
1
2
3
x
0
1
4
9
y
0
1
2
3
[xi,xi+1]
1
1/3
1/5
[xi,..,xi+2]
–1/6
–1/60
[xi,..,xi+3]
1/60
Результат:
1
1
P3 x 0 1 x 0 x 0 x 1 x 0 x 1 x 4
6
60
1
1
x x x 1 x x 1 x 4
6
60

26. Примеры

Полином Ньютона.
1
1
P3 x x x x 1 x x 1 x 4
6
60
Проверка:
1
P3 0 0; P3 1 1; P3 4 4 4 3 4 2 2;
6
1
1
P3 9 9 9 8 9 8 5 9 12 6 3
6
60

27. Примеры

Полином Ньютона.
1
1
P3 x x x x 1 x x 1 x 4
6
60
Значения в узлах результирующей сетки:
1 1 1 1 1 1 1 1 1
P3 1 1 4
4 4 6 4 4 60 4 4 4
9 9 1 9 9 1 9 9 9
P3 1 1 4
4 4 6 4 4 60 4 4 4
75
0.293
256
435
1.699
256
25 25 1 25 25 1 25 25 25
515
P3
1 1 4
2.012
4 4 6 4 4
60 4 4
4
256

28. Примеры

Полином Лагранжа.
f x x
i
x
y
0
0
0
1
1
1
2
4
2
3
9
3
Результирующая сетка: {1/4, 9/4, 25/4}
Далее строим полином L3(x).

29. Примеры

Полином Лагранжа.
i
x
y
0
0
0
ci
1
1
1
2
4
2
3
9
3
yi
x x
n
j 0
j i
i
j
0
1
1
c0
0; c1
;
0 1 0 4 0 9
1 0 1 4 1 9 24
2
1
3
1
c2
; c3
4 0 4 1 4 9 30
9 0 9 1 9 4 120

30. Примеры

Полином Лагранжа.
1
1
1
c0 0; c1 ; c2 ; c3
24
30
120
Результат:
1
L3 x 0 x 1 x 4 x 9 x 0 x 4 x 9
24
1
1
x 0 x 1 x 9
x 0 x 1 x 4
30
120
1
1
1
x x 4 x 9 x x 1 x 9
x x 1 x 4
24
30
120

31. Примеры

Полином Лагранжа.
1
1
1
L3 x
x x 4 x 9 x x 1 x 9
x x 1 x 4
24
30
120
Проверка:
1
L3 0
0 0 4 0 9
1
1
0 0 1 0 9
0 0 1 0 4 0
24
30
120
1
1
1
L3 1 1 1 4 1 9 1 1 1 1 9
1 1 1 1 4 1
24
30
120
1
1
1
L3 4
4 4 4 4 9 4 4 1 4 9
4 4 1 4 4 2
24
30
120
1
1
1
L3 9 9 9 4 9 9 9 9 1 9 9
9 9 1 9 4 3
24
30
120

32. Примеры

Полином Лагранжа.
1
1
1
L3 x
x x 4 x 9 x x 1 x 9
x x 1 x 4
24
30
120
Значения в узлах результирующей сетки:
1 1 1 1
1
1 1 1 1
L3 4 9 1 9
4 24 4 4
4
30 4 4 4
1 1 1 1
75
9 1 9 9
9
1 4
; L3 4 9
120 4 4 4
256
4 24 4 4
4
1 9 9 9
1 9 9 9
435
1 9
1 4
30 4 4 4
120 4 4 4
256

33. Примеры

Полином Лагранжа.
1
1
1
L3 x
x x 4 x 9 x x 1 x 9
x x 1 x 4
24
30
120
Значения в узлах результирующей сетки:
25 1 25 25
25
1 25 25 25
L3 4 9 1 9
4 24 4 4
4
30 4 4
4
1 25 25 25
515
1 4
120 4 4
4
256

34. Примеры

Точность интерполяции:
x
P(x)
L(x)
f (x)
δ
1/4
9/4
25/4
0.293
1.699
2.012
0.293
1.699
2.012
0.5
1.5
2.5
41.4%
13.3%
19.5%