Similar presentations:
Численное дифференцирование
1.
2. Дифференцирование с помощью разностных соотношений
[a, b] : xi a ih , i 0, n; hn b aU ( xi ), i 0, n
U x ,i
U x ,i
U ( xi ) U ( xi 1 )
h
1
-левая разностная производная
функции U(x) в точке x=xi
U ( xi 1 ) U ( xi )
h
2
-правая разностная производная
функции U(x) в точке x=xi
3
U x ,i
U ( xi 1 ) U ( xi 1 ) -центральная разностная производная
функции U(x) в точке x=xi
2h
3. Погрешность разностных формул
U ( )2
U ( x) U ( xi ) U ( xi )( x xi )
( x xi ) , [ x, xi ]
2
U ( x) U ( xi ) U ( )
U ( xi )
( x xi )
x xi
2
4
x xi 1 :
U ( xi ) U ( xi 1 ) U ( i )
U ( xi )
( xi xi 1 ), i [ xi 1 , xi ]
xi xi 1
2
h
U ( xi ) U x ,i U ( i )
2
4.
hU ( xi ) U x ,i U ( i ), i [ xi 1 , xi ]
2
p 1
1.1
h
U ( xi ) U x ,i U ( i ), i [ xi , xi 1 ]
2
p 1
2.1
h
U ( xi ) U x ,i U ( i ), i [ xi 1 , xi 1 ] p 2
6
3.1
2
U x x ,i
U ( xi 1 ) 2U ( xi ) U ( xi 1 )
1
(U x ,i U x ,i )
h
h2
U x x ,i
h 2 ( 4)
U ( xi ) U ( i ), i [ xi 1 , xi 1 ]
12
5. Уточнение результата методом Рунге
hU ( xi ) U x ,i U ( i ), i [ xi 1 , xi ]
2
U (x) производная функции U(x) (точное значение)
U x ,h ( x) разностное соотношение, вычисленное с шагом h
R h p ( x) (h p 1 )
U ( x) U x,h h p ( x) (h p 1 )
h1 kh :
h ( x)
p
5
U ( x) U x,kh (kh) p ( x) ((kh) p 1 )
U x,h U x,kh
k p 1
(h p 1 )
U ( x) U x,h
6
U x,h U x,kh
k p 1
(h p 1 )
6. Выбор шага дифференцирования
U ( xi 1 ) U ( xi ) hU ( xi )
U ( i )
h
2
U(xi) – приближенное значение функции U(x) в точке xi
~
U ( xi ) - точное значение функции U(x) в точке xi
~
U ( xi ) U ( xi )
~
U ( xi ) [U ( xi ) ,U ( xi ) ]
2
h
U ( xi 1 ) U ( xi ) 2 M 2
U ( xi )
h
h
h
2
M2
h,
2
M 2 max U ( x )
x [ xi , xi 1 ]
7.
2 M 2g ( h)
h min
h
2
- функция полной погрешности
h 0 g ( h)
h
g ( h)
2 M 2
g (h) 2
0
h
2
hopt 2
M2
8. Дифференцирование с помощью интерполяционных многочленов
a x0 x1 xn b; U ( xi ); hi xi xi 1L2,i
x xi ( x xi 1 )
U (x
i 1
hi (hi hi 1 )
x xi 1 ( x xi )
U (x
hi 1 (hi hi 1 )
L2 ,i
i 1
i 1
hi (hi hi 1 )
2 x xi 1 xi
U (x
i
hi hi 1
)
2 x xi xi 1
U (x
hi 1 (hi hi 1 )
x xi 1 ( x xi 1 )
)
U (x )
i 1
)
2 x xi 1 xi 1
)
U (x )
hi hi 1
i
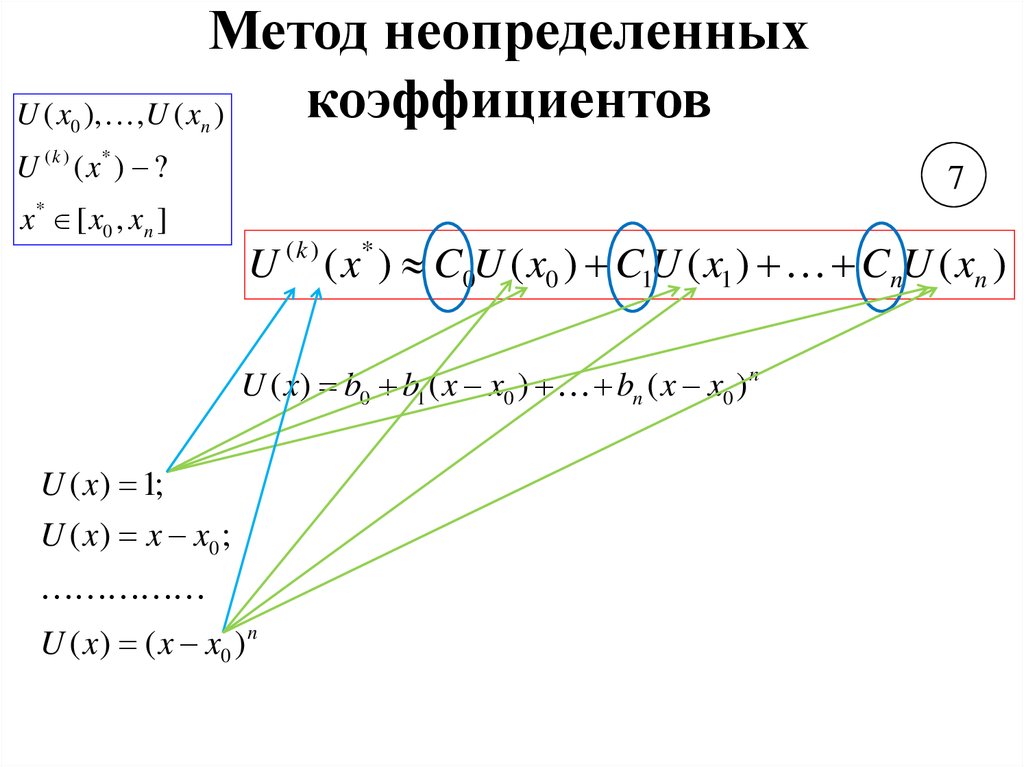
9. Метод неопределенных коэффициентов
U ( x ), , U ( x )0
n
U ( k ) ( x* ) ?
x * [ x0 , x n ]
7
U ( k ) ( x* ) C0U ( x0 ) C1U ( x1 ) CnU ( xn )
U ( x) b0 b1 ( x x0 ) bn ( x x0 ) n
U ( x) 1;
U ( x) x x0 ;
U ( x) ( x x0 ) n
10.
x* [ x0 , x3 ], U ( xi ), i 0,3U ( x* ) C0U ( x0 ) C1U ( x1 ) C2U ( x2 ) C3U ( x3 )
U ( x ) x x0 ;
U ( x) 0;
U ( x) 1;
U ( x ) ( x x0 ) 2 ;
U ( x) 2( x x0 );
U ( x ) ( x x0 ) 3
U ( x) 3( x x0 ) 2
U ( x ) 1;
7.1
x x*
0 C0 1 C1 1 C2 1 C3 1
1 C ( x x ) C ( x x ) C ( x x ) C ( x x )
0
0
0
1 1
0
2
2
0
3
3
0
*
2
2
2
2
2
(
x
x
)
C
(
x
x
)
C
(
x
x
)
C
(
x
x
)
C
(
x
x
)
0
0
0
0
1
1
0
2
2
0
3
3
0
3( x* x ) 2 C ( x x )3 C ( x x )3 C ( x x )3 C ( x x )3
0
0
0
0
1 1
0
2
2
0
3
3
0
11. Вычисление частных производных
U f ( x, y) :U ij f ( xi , y j ), xi x0 ih1 , i 0, I ;
y j 1
…
xi 1
xi
xi 1
…
yj
y j 1
…
…
…
U i 1, j 1 U i 1, j U i 1, j 1
…
U i , j 1
…
…
U ij
U i , j 1
U i 1, j 1 U i 1, j U i 1, j 1
…
…
…
2U U i 1, j 2U ij U i 1, j
2
2
x
h
ij
1
y j y0 jh2 , j 0, J
( xi , y j ) ?
…
…
…
…
…
U i 1, j U ij
U
h1
x ij
U i , j U i 1, j
U
h1
x ij
U U i , j 1 U ij
h2
y ij
12.
y j 1…
xi 1
xi
xi 1
…
yj
y j 1
…
…
…
U i 1, j 1 U i 1, j U i 1, j 1
…
U i , j 1
…
…
U ij
U i , j 1
U i 1, j 1 U i 1, j U i 1, j 1
…
…
…
…
…
…
…
…
U i 1, j 1 U i 1, j 1 U i 1, j 1 U i 1, j 1
2U
4h1 h2
x y ij











 mathematics
mathematics








