Определители. Обратная матрица. Лекция 2

1.

Определители.
Обратная матрица
Лекция 2

2.

Определитель матрицы
Квадратной матрице А порядка n можно поставить в
соответствие число detA (или ∆, или |A|), называемое её
определителем
n 1,
A a1 , det A a1

3.

Определители 2-го порядка
Определитель второго порядка равен произведению
элементов, расположенных на главной диагонали минус
произведение элементов, расположенных на дополнительной
диагонали.
а11 а12
А
а
а
21 22
а11 а12
det( A)
а11а22 а12 а21
а21 а22
2 3
2 5 3 4 10 12 2
4 5

4.

Определители 3-го порядка
Определитель третьего порядка равен произведению
элементов, расположенных на главной диагонали плюс два
произведения элементов, отвечающих треугольникам с
основаниями, параллельными главной диагонали; минус
произведение элементов, расположенных на дополнительной
диагонали и минус два произведения элементов, отвечающих
треугольникам
с
основаниями,
параллельными
дополнительной диагонали.
a11 a12
a21 a22
a31 a32
a13
a23 a11a22 a33 a12a23a31 a13a21a32 a13a22a31 a11a23a32 a12a21a33
a33

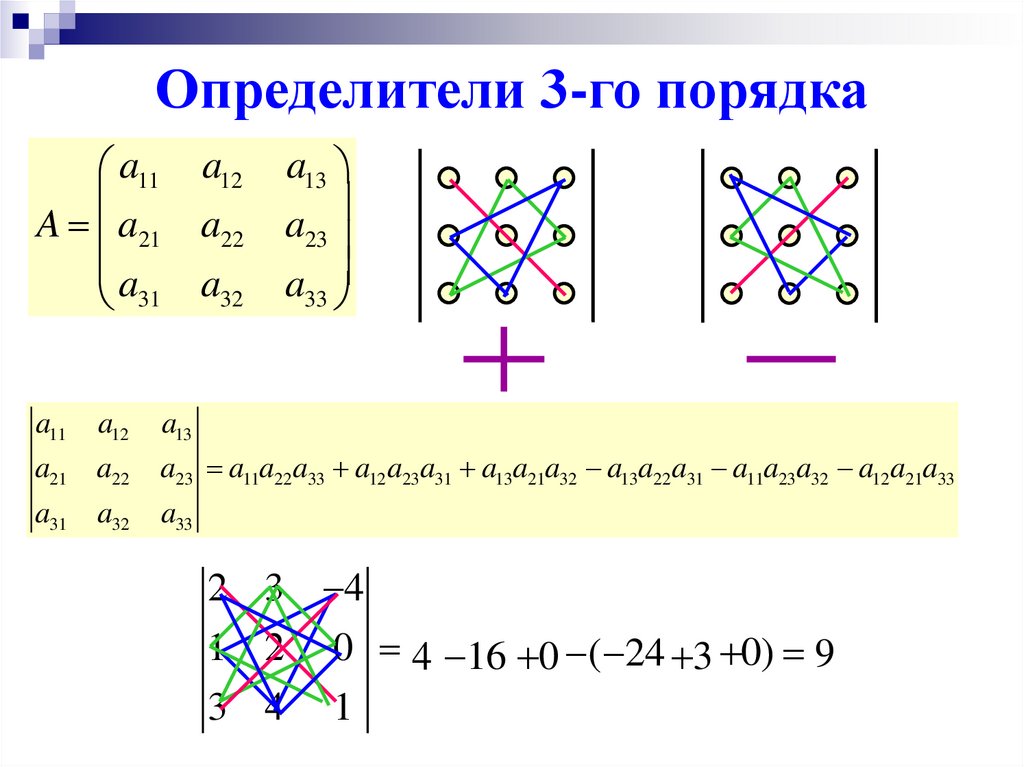
5.

Определители 3-го порядка
a11 a12
A a21 a22
a
31 a32
a11 a12
a21 a22
a31 a32
a13
a23
a33
a13
a23 a11a22 a33 a12a23a31 a13a21a32 a13a22a31 a11a23a32 a12a21a33
a33
2 3 4
1 2 0 44 16
0
16
(24
03 30)
99
24
0
3 4 1

6.

Правило треугольника
a11 a12
A a21 a22
a
31 a32
a13
a23
a33

7.

Правило Саррюса
a11 a12
A a21 a22
a
31 a32
a11 a12
a21 a22
a31 a32
a13
a23
a33
a11 a12
a21 a22
a31 a32
a13 a11 a12
a23 a21 a22
a33 a31 a32
a13
a23 a11a22 a33 a12a23a31 a13a21a32 a13a22a31 a11a23a32 a12a21a33
a33
2 4 3
2 5 3
3 5 6
2 4
2 5 2∙5∙6 + 4∙3∙3+3∙2∙(-5) -3∙5∙3 -2∙3∙(-5)-4∙3∙6= - 21
3 5

8.

Свойства определителей
1. Величина определителя не изменится, если его
строки поменять местами с соответствующими
столбцами, т.е. транспонировать
a1
a2
a3
b1
b2
b3
c1 a1 a2
c2 b1 b2
c3 c1 c2
a3
b3
c3

9.

Свойства определителей
2. При перестановке местами двух строк (столбцов)
определитель
меняет
свой
знак
на
противоположный.
с1
с2
с3
b1
b2
b3
а1
a1
а2 a2
а3
a3
b1
b2
b3
c1
c2
c3

10.

Свойства определителей
3. Определитель, имеющий две одинаковые строки
(столбца), равен нулю.
a1
a2
a3
а1
а2
а3
c1
c2 0
c3

11.

Свойства определителей
4. Если все элементы какой-либо строки (столбца)
определителя умножить на одно и то же число, то и
определитель умножается на это число.
a1 b1 c1
a2
a3
b2
b3
a1
c2 a2
c3
a3
b1
b2
b3
c1
c2
c3

12.

Свойства определителей
5. Если все элементы некоторой строки (столбца)
определителя равны нулю, то и сам определитель
равен нулю.
a1
a2
a3
0 c1
0 c2 0
0 c3

13.

Свойства определителей
6. Определитель, у которого элементы двух его
строк (столбцов) пропорциональны, равен нулю.
a1
a2
a3
kа1
kа2
kа3
c1
a1
( 4)
c2 k a2
c3
a3
а1
а2
а3
c1
(3)
c2 k 0 0
c3

14.

Свойства определителей
7. Если каждый элемент какой-либо строки
(столбца) определителя есть сумма двух слагаемых,
то определитель равен сумме двух определителей, у
одного из них элементами соответствующей строки
являются первые слагаемые, у другого – вторые.
Оставшиеся элементы этих определителей те же,
что и у данного.
a1
a2
a3
b1
b2
b3
c1 d1 a1
c2 d 2 a2
c3 d3 a3
b1
b2
b3
c1 a1
c2 a2
c3 a3
b1
b2
b3
d1
d2
d3

15.

Свойства определителей
8. Определитель не изменится, если к элементам
какой-либо его строки (столбца) прибавить
соответствующие
элементы
другой
строки
(столбца), умноженные на одно и то же число.
a1 b1
a2 b2
a3 b3
b1
b2
b3
c1 a1
(7)
c2 a2
c3 a3
b1
b2
b3
c1 b1
c2 b2
c3 b3
b1
b2
b3
c1
(4)
c2
c3
a1
(4)
a2
a3
b1
b2
b3
c1
b1
c2 b2
c3
b3
b1
b2
b3
c1 a1
(3)
c2 a2
c3 a3
b1
b2
b3
c1
c2
c3

16.

Минор
Минором Mij элемента aij определителя n-го порядка
называется определитель (n–1)-го порядка, который
получается в результате вычеркивания в определителе n-го
порядка строки и столбца, на пересечении которых
находится элемент aij.
a11 a12 a13
a21 a22 a23
a31 a32 a33
a22 a23
M 11
a32 a33
a11 a13
M 32
a21 a23

17.

Алгебраическое дополнение
Алгебраическим дополнением Aij элемента aij
определителя называется его минор Mij, взятый со знаком
(–1)i+j.
Aij ( 1)i j M ij
a11 a12 a13
a21 a22 a23
a31 a32 a33
a22 a23
А11
a32 a33
a11 a13
А32
a21 a23

18.

Теорема о разложении
определителя по элементам
строки или столбца
Определитель равен сумме произведений всех
элементов произвольной его строки (или столбца) на их
алгебраические дополнения. Иначе говоря, имеет место
следующее разложение определителя по элементам
i-й строки
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
или j- го столбца
a1 j A1 j a2 j A2 j anj Anj , ( j 1, , n)

19.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
( 2 1 1 3) 2 (0 1 3 3)
3 1
(0 1 3 2) 5 18 6 19

20.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
( 2 1 1 3) 2 (0 1 3 3)
3 1
(0 1 3 2) 5 18 6 19

21.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
( 2 1 1 3) 2 (0 1 3 3)
3 1
(0 1 3 2) 5 18 6 19

22.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
3 1
(0 1 3 2) 5 18 6 19

23.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
( 2 1 1 3) 2 (0 1 3 3)
3 1
(0 1 3 2)

24.

1 2 1
A 0 2 3
3 1 1
ai1 Ai1 ai 2 Ai 2 ain Ain , (i 1, , n)
1 2 1
3
3
1 1 2
1 2 0
0 2 3 1 ( 1)
2 ( 1)
1 1
3 1
3 1 1
1 3
1 ( 1)
0 2
( 2 1 1 3) 2 (0 1 3 3)
3 1
(0 1 3 2) 5 18 6 19

25.

Пример
2
2
1
5
2
1
1
2
0
3
0
1
1
4
2
0

26.

Пример
2
2
1
5
2
1
1
2
0
3
0
1
1
4
а13 А13 а23 А23 а33 А33 а43 А43
2
0
2 1 4
2 2 1
0 ( 1)1 3 1 1 2 3 ( 1) 2 3 1 1 2
5 2 0
5 2 0
2 2 1
2 2 1
0 ( 1)3 3 2 1 4 1 ( 1) 4 3 2 1 4
5 2 0
1 1 2
3 (20 2 5 8) 1 (4 8 2 1 8 8) 3 9 ( 3) 24

27.

Обратная матрица
a11 a12 ... a1 n
a21 a22 ... a2 n
A
... ... ... ...
an 1 an 2 ... an n
Квадратная
матрица
А
называется невырожденной, или
неособенной,
если
ее
определитель отличен от нуля, и
вырожденной, или особенной,
если = 0.
Квадратная матрица А-1 называется обратной для
квадратной матрицы А того же порядка, если их
произведение А А-1 = А-1 А = Е, где Е - единичная матрица
того же порядка, что и матрица А.

28.

Обратная матрица
Теорема. Для того, чтобы матрица А имела обратную,
необходимо и достаточно, чтобы ее определитель был
отличен от нуля.
Обратная матрица вычисляется по формуле
A11 A21 ... An 1
1 A12 A22 ... An 2
1
A
... ... ... ...
A1 n A2 n ... An n
где А ij – алгебраические дополнения элементов a ij.

29.

Обратная матрица
a11 a12 ... a1 n
a21 a22 ... a2 n
A
... ... ... ...
an 1 an 2 ... an n
2 -2 1
A 2 1 -2
1 2 2
A11 A21 ... An 1
1 A12 A22 ... An 2
1
A
... ... ... ...
A1 n A2 n ... An n
2
= det А = 2
1
-2 1
1 -2
2 2
= 27 0

30.

Обратная матрица
2 -2 1
A 2 1 -2
1 2 2
1+1 1
A22 ( 1)
2+ 2 2
1
1
4 1 3,
2
2+3 2
-2
A23 ( 1)
(4 2) 6,
1 2
3+1 2 1
A31 ( 1)
4 1 3,
1 -2
-2
A11 ( 1)
2 4 6,
2 2
1
3+2 2
1+2 2 -2
A12 ( 1)
(4 2) 6, A32 ( 1) 2 - 2 ( 4 2) 6,
1 2
1
1+3 2
3+3 2 -2
A13 ( 1)
4 1 3,
A33 ( 1)
2 4 6
1 2
2 1
A21 ( 1)
2+1
2
2
1
( 4 2) 6,
2

31.

Обратная матрица
2 -2 1
A 2 1 -2
1 2 2
A11 A21 ... An 1
1 A12 A22 ... An 2
1
A
... ... ... ...
A1 n A2 n ... An n
= det А = 27 0
6
6
1
1
А -6 3
27
3 -6
3
2
2
1
6 -2 1
9
6
1 -2
1
2
2

32.

Свойства обратных матриц
1. (A-1)-1 = A;
2. (AB)-1 = B-1A-1
3. (AT)-1 = (A-1)T.

33.

Пример
1 2 0
А 0 3 1 .
0 1 2
Найти матрицу А-1