Similar presentations:
Двугранный угол. Перпендикулярность плоскостей. Урок 12
1.
2.
3.
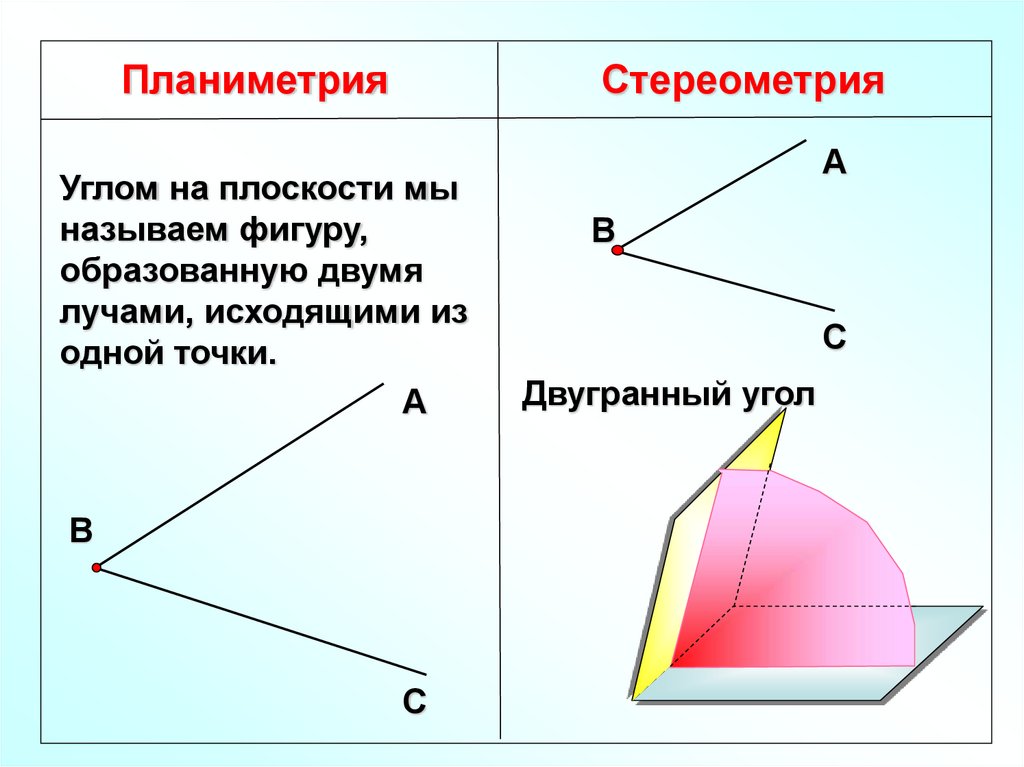
ПланиметрияСтереометрия
Углом на плоскости мы
называем фигуру,
образованную двумя
лучами, исходящими из
одной точки.
А
В
С
А
В
С
Двугранный угол
4.
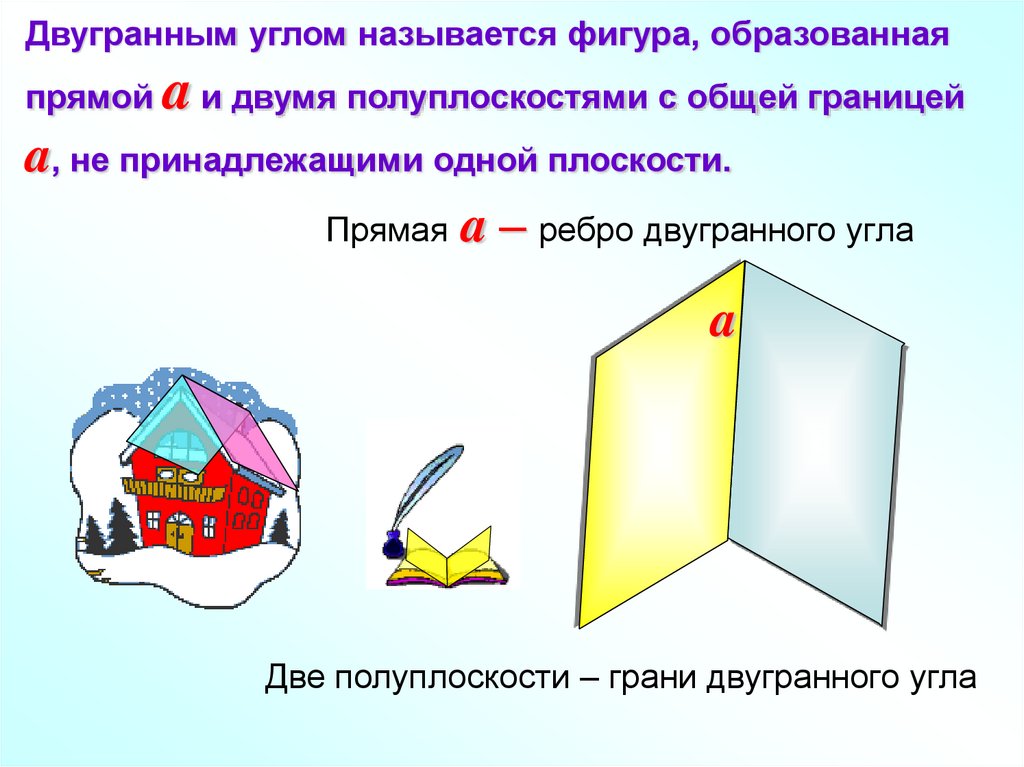
Двугранным углом называется фигура, образованнаяпрямой
a и двумя полуплоскостями с общей границей
a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла
5.
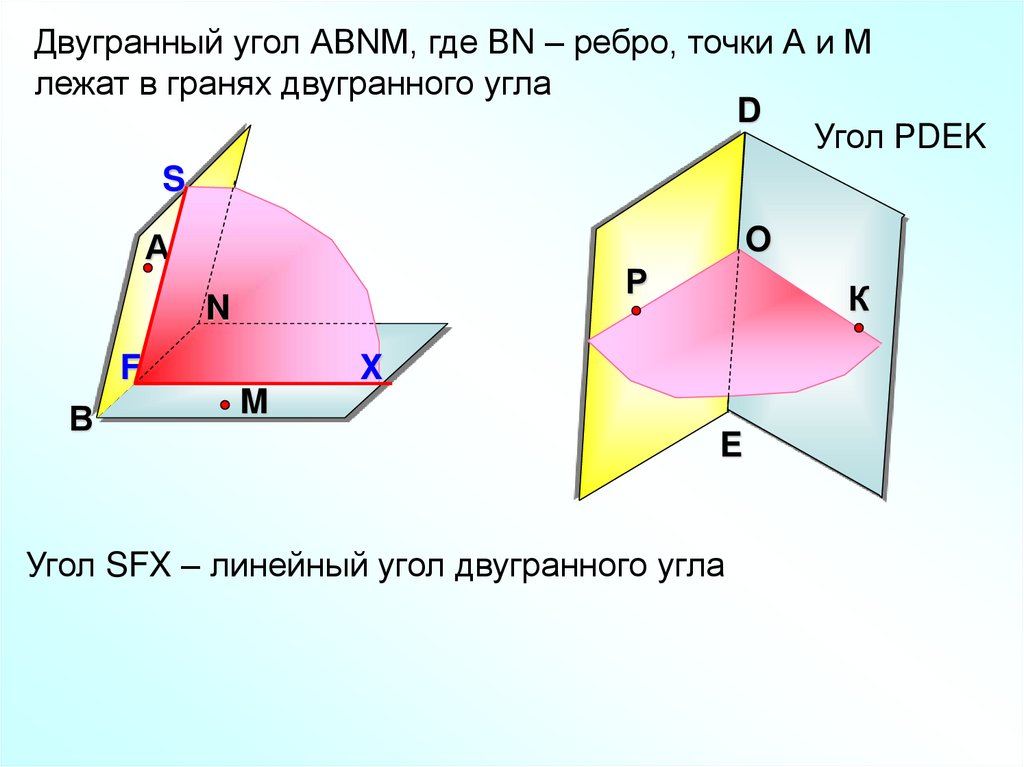
Двугранный угол АВNМ, где ВN – ребро, точки А и Млежат в гранях двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
К
X
M
E
Угол SFX – линейный угол двугранного угла
6.
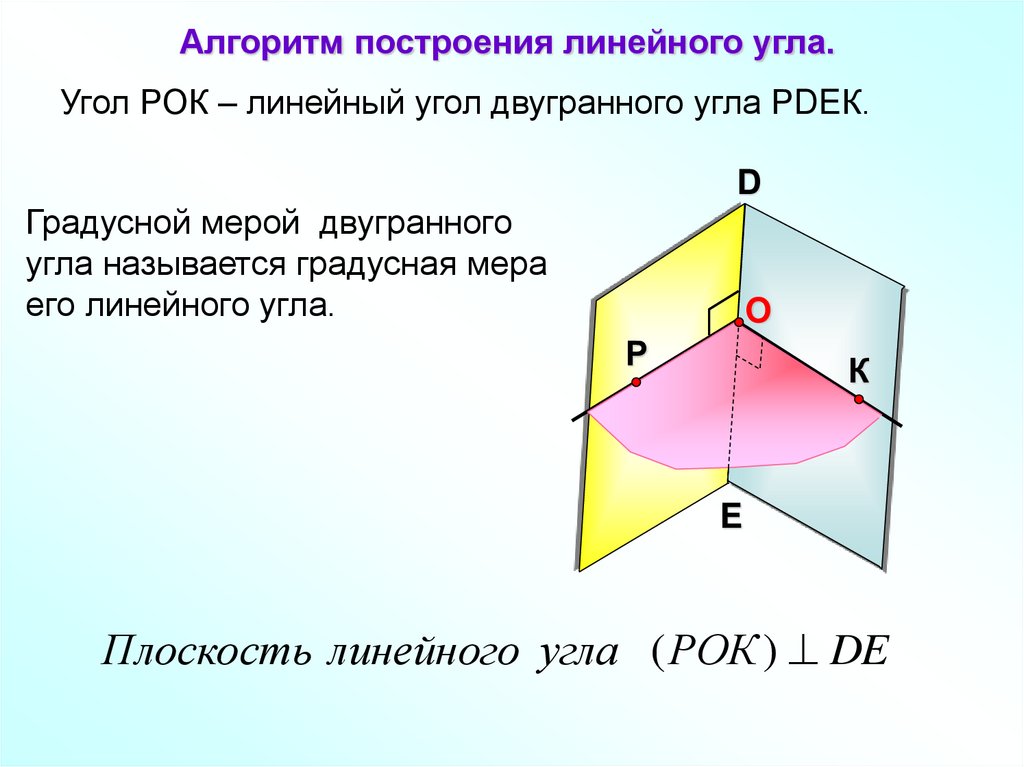
Алгоритм построения линейного угла.Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного
угла называется градусная мера
его линейного угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE
7.
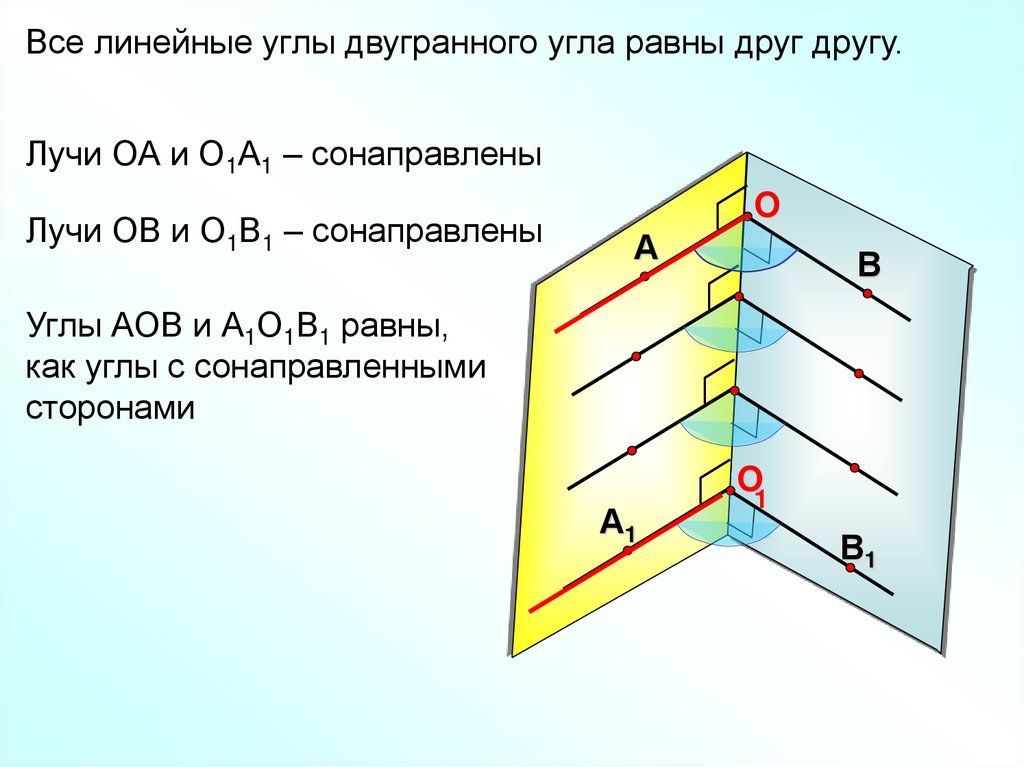
Все линейные углы двугранного угла равны друг другу.Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
O
А
В
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными
сторонами
O
А1
1
В1
8.
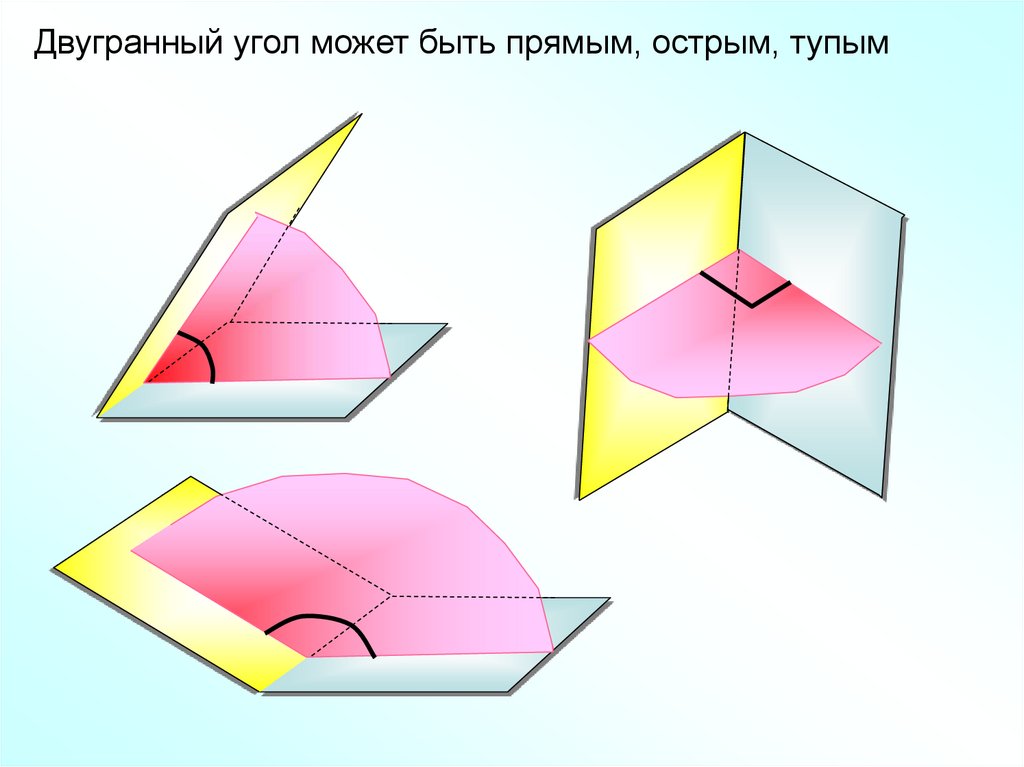
Двугранный угол может быть прямым, острым, тупым9.
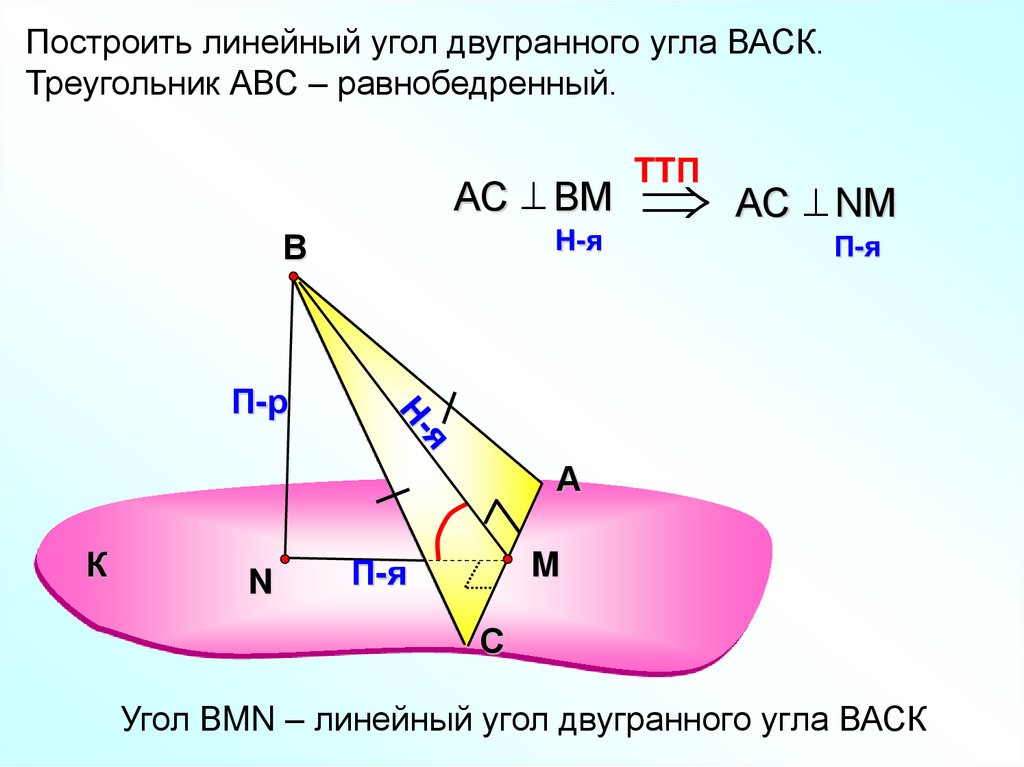
Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.
АС ВМ АС NМ
TTП
В
H-я
П-я
П-р
А
К
N
M
П-я
С
Угол ВMN – линейный угол двугранного угла ВАСК
10.
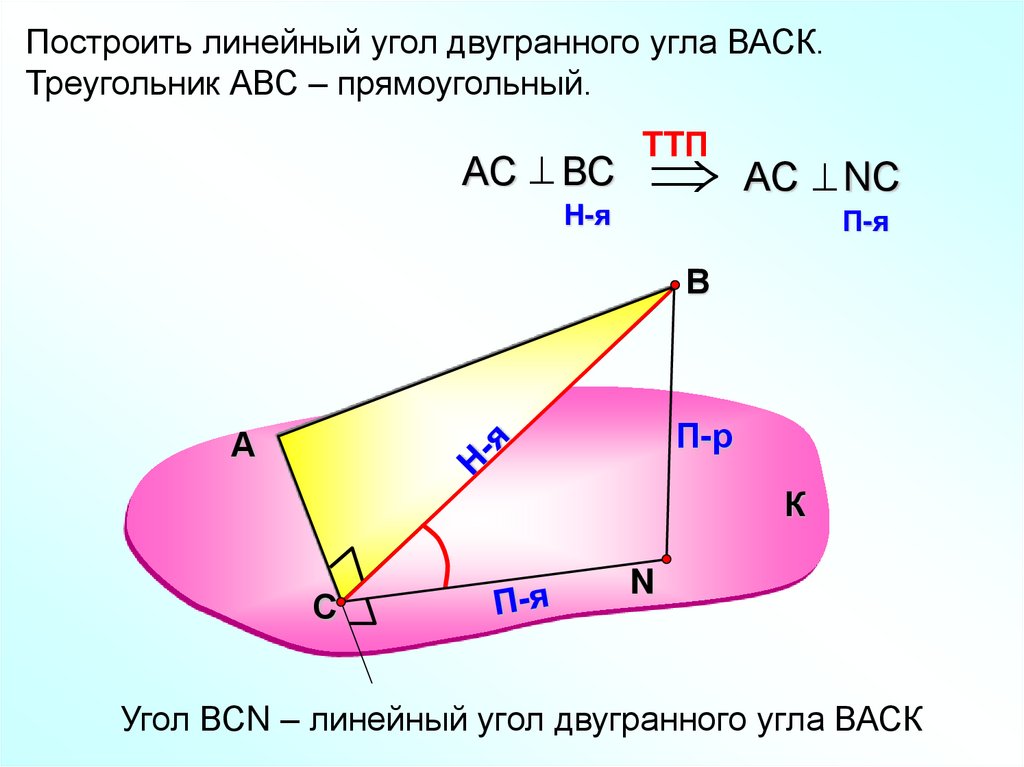
Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.
АС ВС
H-я
АС NС
TTП
П-я
В
П-р
А
К
С
N
Угол ВСN – линейный угол двугранного угла ВАСК
11.
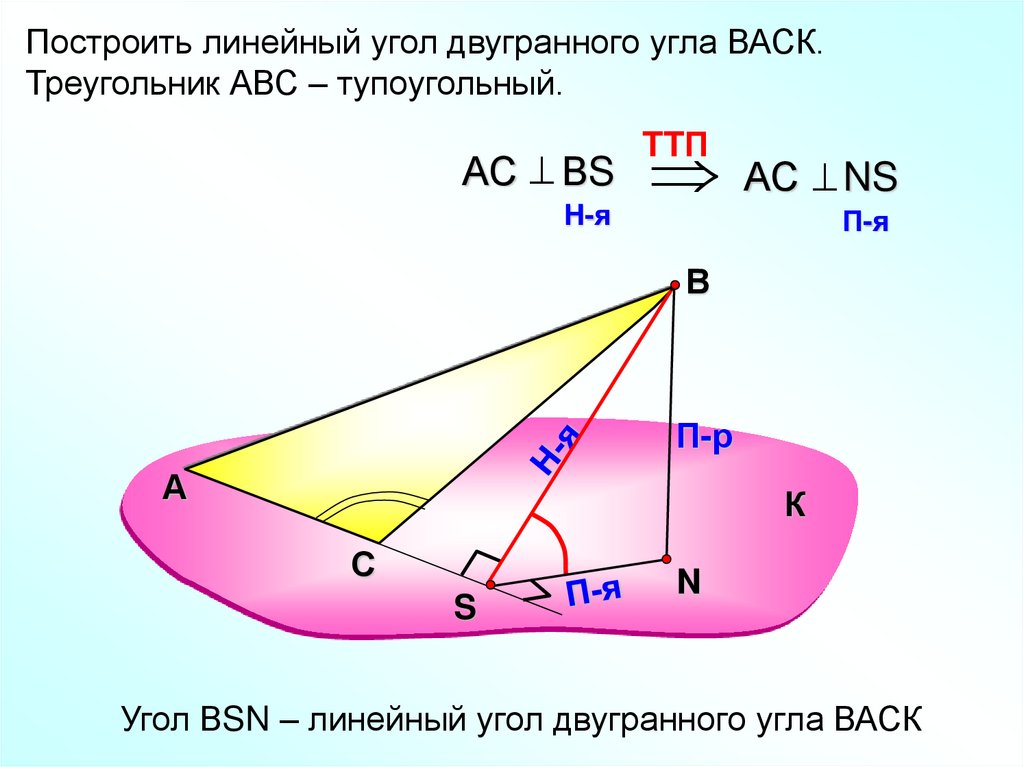
Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.
АС ВS
H-я
АС NS
TTП
П-я
В
П-р
А
К
С
S
N
Угол ВSN – линейный угол двугранного угла ВАСК
12.
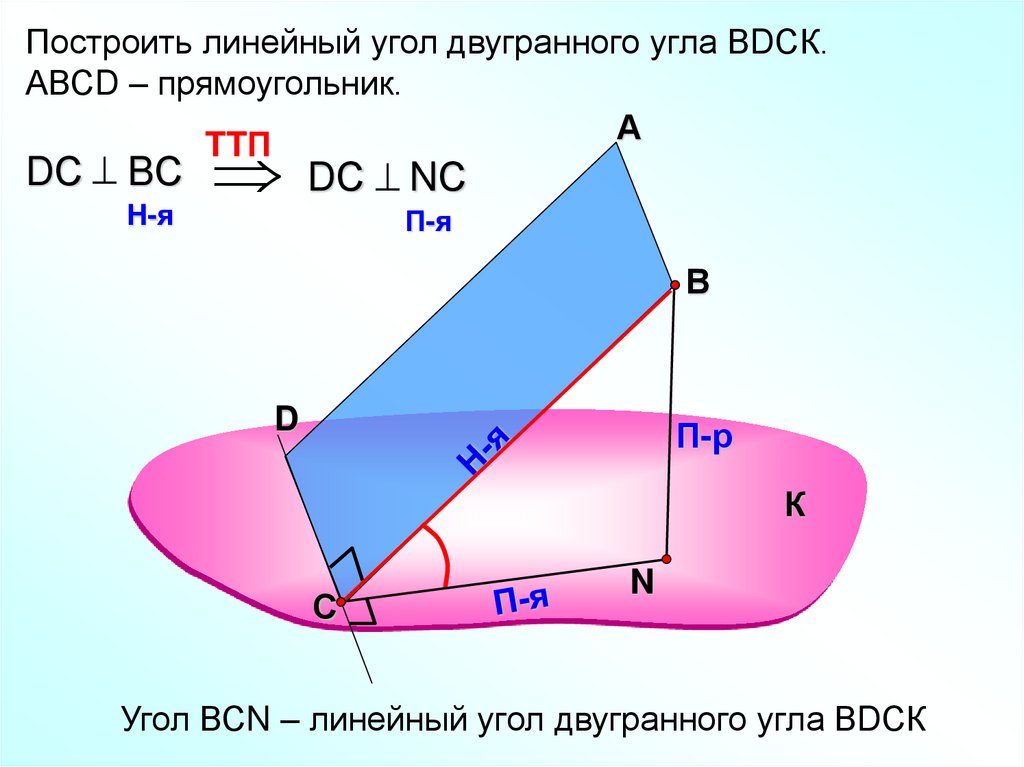
Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.
А
TTП
DС BС
H-я
DС NС
П-я
В
D
П-р
К
С
N
Угол ВСN – линейный угол двугранного угла ВDСК
13.
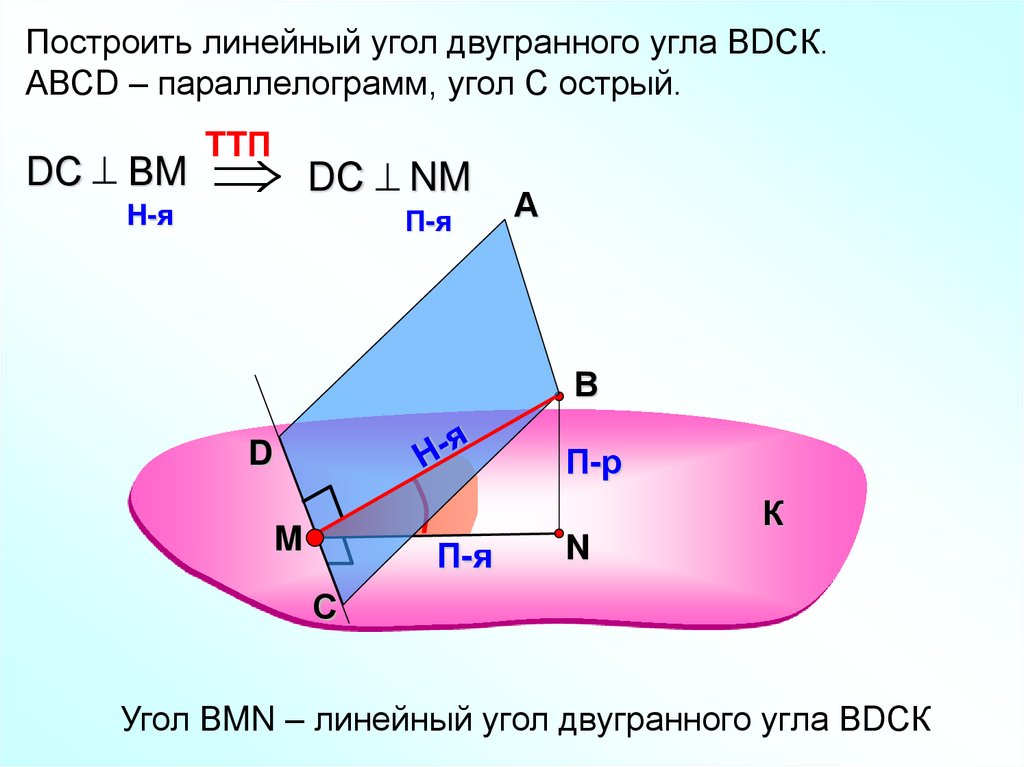
Построить линейный угол двугранного угла ВDСК.АВСD – параллелограмм, угол С острый.
DС ВM DС NM
TTП
H-я
П-я
А
В
D
П-р
К
M
П-я
N
С
Угол ВMN – линейный угол двугранного угла ВDСК
14.
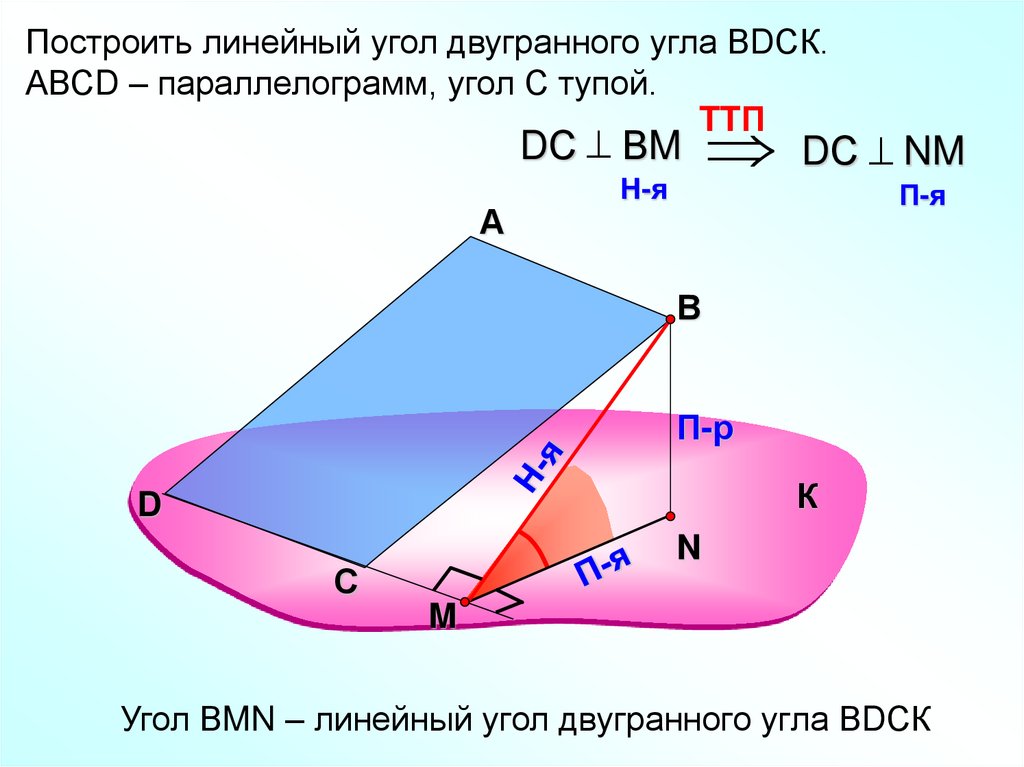
Построить линейный угол двугранного угла ВDСК.АВСD – параллелограмм, угол С тупой.
TTП
DС ВM DС NM
А
H-я
П-я
В
П-р
К
D
N
С
M
Угол ВMN – линейный угол двугранного угла ВDСК
15.
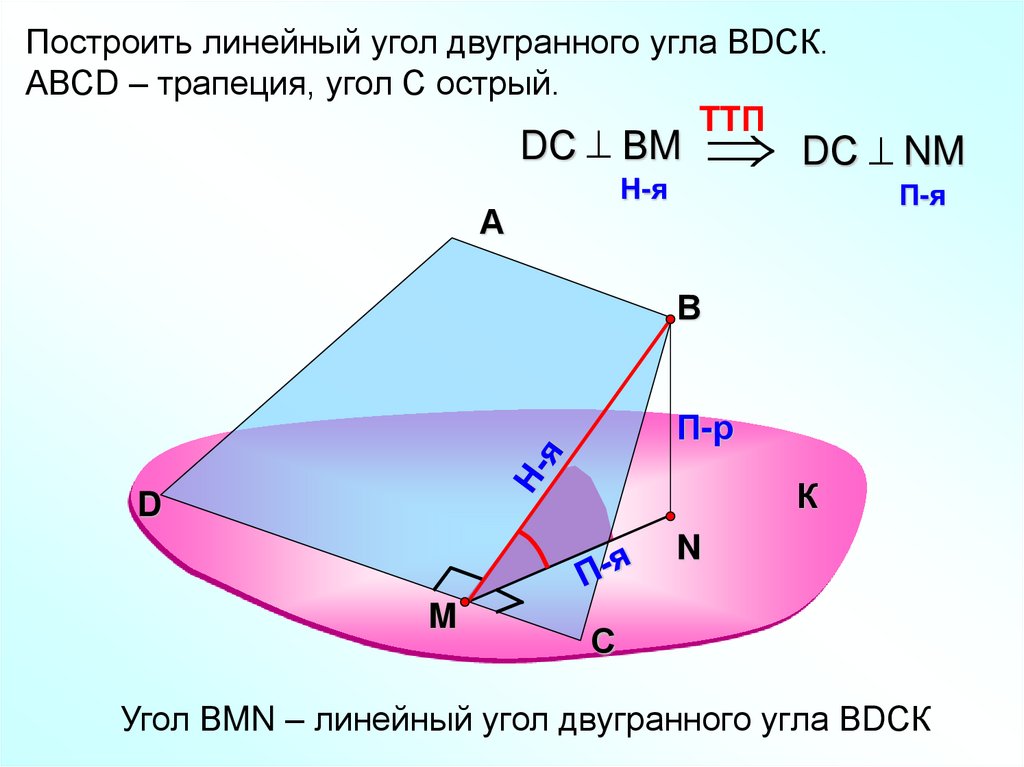
Построить линейный угол двугранного угла ВDСК.АВСD – трапеция, угол С острый.
TTП
DС ВM DС NM
H-я
А
П-я
В
П-р
К
D
N
M
С
Угол ВMN – линейный угол двугранного угла ВDСК
16.
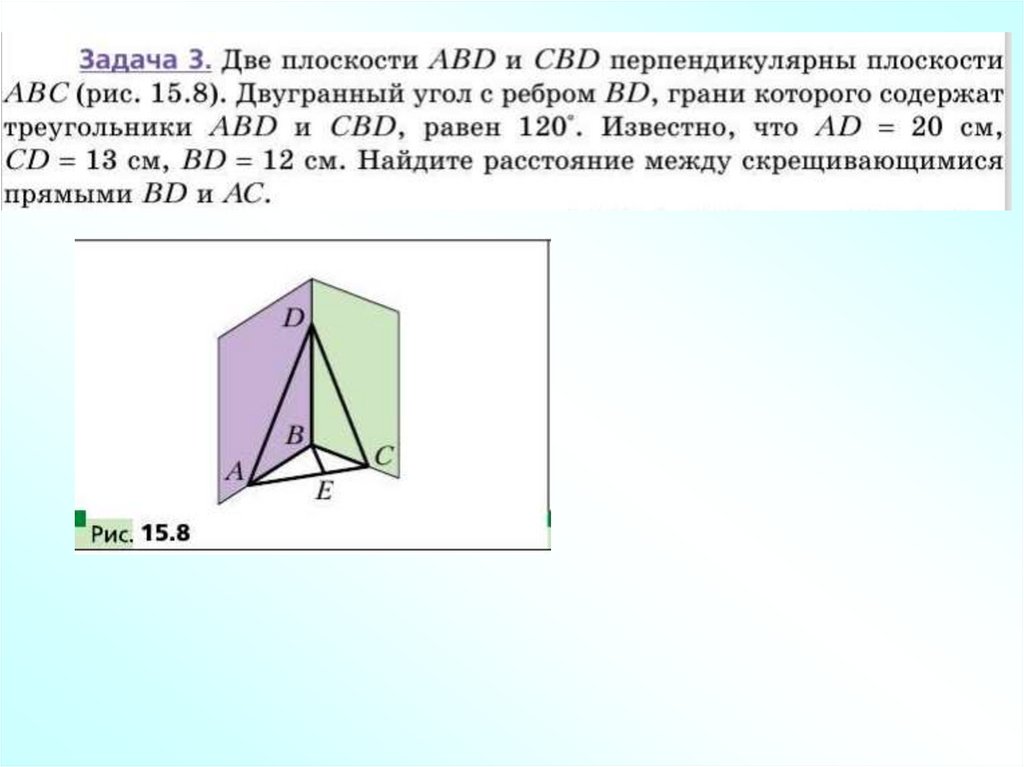
17. Решение задач
18. Решение задач
19. Решение задач
20. Решение задач
21. Решение задач
22.
23.
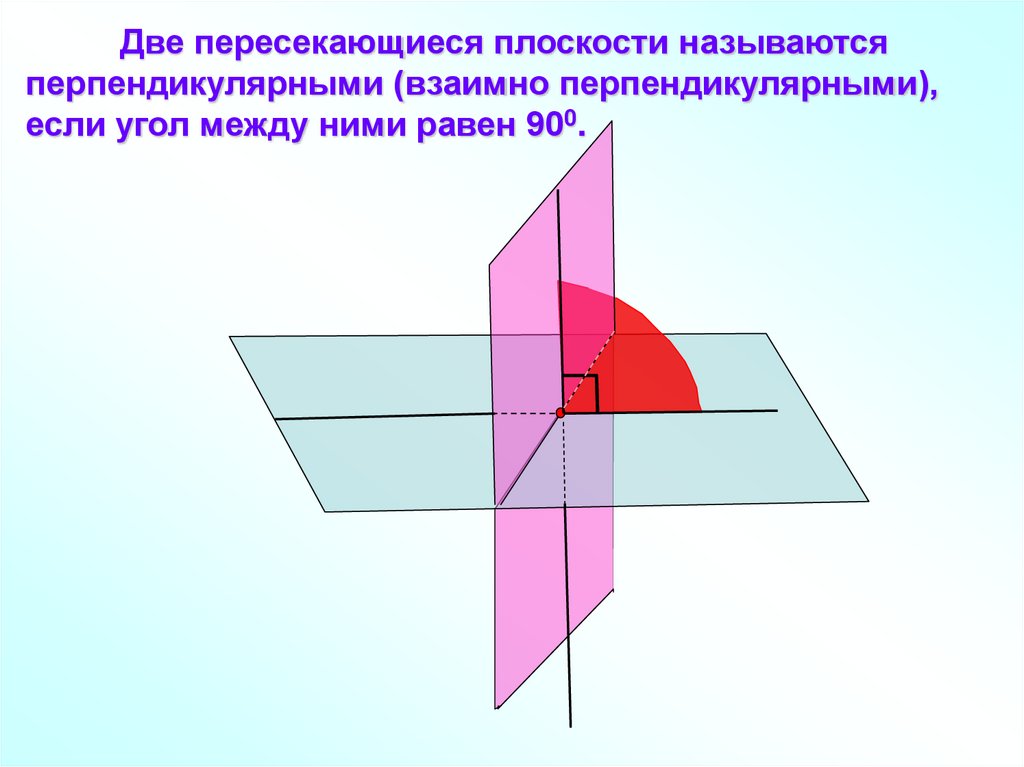
Две пересекающиеся плоскости называютсяперпендикулярными (взаимно перпендикулярными),
если угол между ними равен 900.
24.
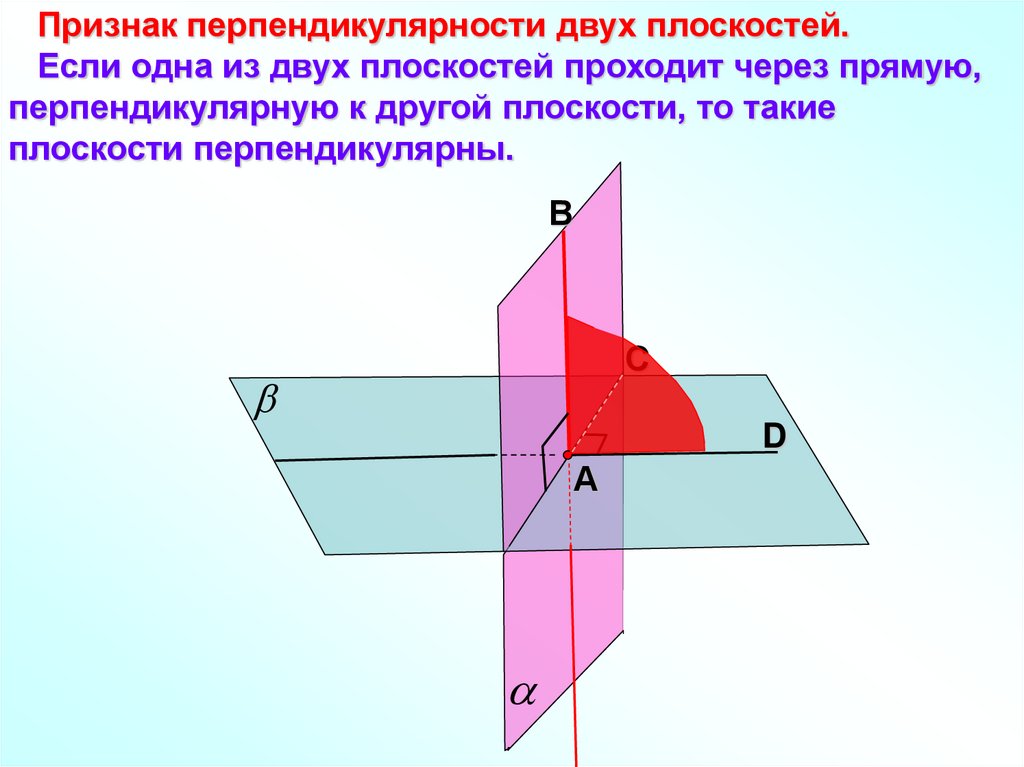
Признак перпендикулярности двух плоскостей.Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
В
С
D
А
25.
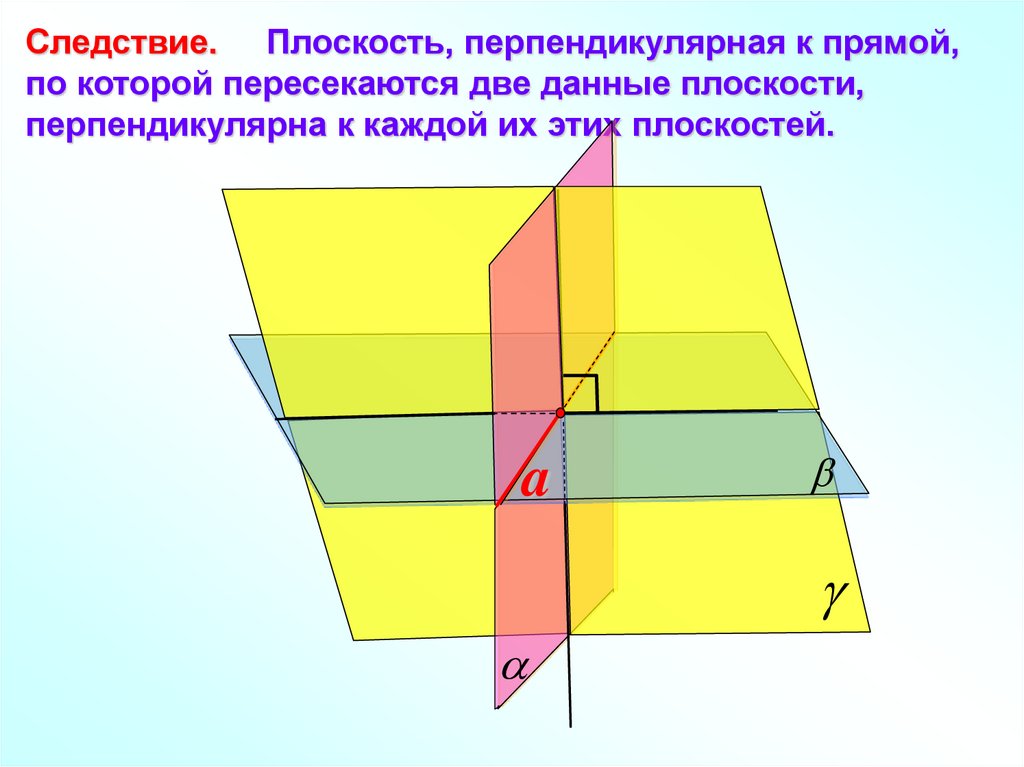
Следствие. Плоскость, перпендикулярная к прямой,по которой пересекаются две данные плоскости,
перпендикулярна к каждой их этих плоскостей.
a
26.
Следствие. Если каждая из двух пересекающихсяплоскостей перпендикулярна к третьей плоскости,
по прямая их пересечения перпендикулярна этой
плоскости.
27.
28.
29. Домашнее задание
• 1) выучить теорию п.22, 23• 2) записать решение №166, 167, 168
• 3) решить №170, 172











 mathematics
mathematics








